扣焓火焰面模型在喷雾燃烧模拟中的应用*

何俊奕, 李 峰, 胡 群, 王利坡

(1. 上海交通大学 密西根学院, 上海 200240;2. 北京动力机械研究所, 北京 100074)

0 引 言

喷雾燃烧是一个极为复杂的过程,涉及包括液滴破碎、燃料蒸发、气液两相流相互作用、湍流-化学反应相互作用和辐射在内的许多物理化学现象．除长度和时间尺度分布范围极广之外,实际工况(例如航空发动机燃烧室)的复杂几何形状也进一步为数值模拟增加了难度．该过程的高精度模拟不仅有助于深入理解复杂的基础燃烧物理,而且对于工业设计也至关重要,尤其是从满足燃烧稳定性、提高燃烧效率和降低污染物水平的现实需求考虑．

复杂燃烧室内喷雾燃烧相关的实验和模拟一直是相关领域研究的热点,近年来也取得了一些进展．Gounder等建立的悉尼喷雾火焰实验模型使用超声波雾化器产生丙酮和乙醇燃料的喷雾射流[1],并测量了不同工况(包括有无化学反应)下的流场和液滴动力学的详细数据,在学术界被认可,用作喷雾燃烧模拟的验证算例．从湍流场计算考虑,主要模型分为Reynolds平均(Reynolds averaged Navier-Stokes,RANS)和大涡模拟(large eddy simulation,LES)两大类．相较于RANS,LES 在燃烧室的设计过程中更受欢迎,因为它的计算量远小于直接数值模拟(direct numerical simulation,DNS),并且能够捕捉非稳态流动特征．湍流燃烧模型经过长期发展,积累了丰富的成果．Yan等使用LES与涡破碎(eddy break-up,EBU)燃烧模型相结合的方法对简化的航空发动机燃烧室进行了模拟[2],预测结果和实验值较为接近,并且可以捕获不同主燃孔位置和进口处燃料/空气混合比的内部燃烧情况差异．Jones等使用LES结合概率密度函数(probability density function,PDF)燃烧模型模拟GENRIG燃烧器中的喷雾燃烧过程[3]．根据结果分析认为,实验数据和模拟结果之间的差异主要由入口喷雾边界条件设置的不确定性导致．本文关注于燃烧模型中受到广泛认可的火焰面模型,将结合模拟结果做分析讨论．

火焰面模型最初由Peters提出,他假设化学反应时间尺度远小于Kolmogorov时间尺度,则三维湍流火焰可以看作是众多一维层流火焰面的系综[4]．由于其以经济高效的方式考虑了详细反应机理,火焰面类方法被广泛用于非预混、预混和部分预混火焰的模拟[5-9]．Moin等将火焰面进程变量(flamelet progress variable,FPV)方法的使用扩展到实际航空发动机燃烧室中喷雾燃烧的大涡模拟中[10]．然而在建表过程中直接使用了纯气相火焰面,并未考虑喷雾的影响．为了解决这一问题从而准确预测气相场温度,Baba等选择总焓作为进程变量,而不是常规选择生成物质量分数[11]．Ma等提出了一种非绝热火焰面生成流形(flamelet generated manifold,FGM)方法,该方法可通过降低氧气侧温度来量化蒸发热损失,并将绝对焓作为附加控制变量在三维程序中求解[12]．最近,Kong等已经将这种方法应用于实际航空发动机燃烧室中喷雾燃烧的模拟[13]．然而当氧气侧温度相对较低时,该方法可能并不适用．Gutheil 等提出的喷雾火焰面模型消除了这种限制,通过对准一维对冲喷雾火焰建表,直接考虑了气液两相相互作用[14-16]．然而,包括初始液滴半径、初始喷雾速度和喷雾入口处的当量比在内的更多控制变量出现在喷雾火焰面库中,使得建表过程变得极为繁琐．另一方面,喷雾火焰面中混合分数的非单调性也增加了查表过程的难度．为此,Franzelli等提出了一种新的混合描述参数[17]．另一种考虑液滴蒸发效应的方法是将蒸发源项与一些已求解变量和预定义参数相关联[18],但这种方法仍缺乏普适性,亟待改进．本文选用的扣焓火焰面模型在三维计算中直接对显焓进行扣焓处理,部分考虑了液滴蒸发与燃烧的耦合效应,适用于复杂工程算例．

本文旨在开发基于OpenFOAM的喷雾燃烧求解器,以悉尼乙醇喷雾火焰标模EtF7为校准,并模拟了真实的航空发动机折流燃烧室．本文主要结构如下:首先介绍了所采用的湍流、燃烧和其他模型,然后使用悉尼乙醇喷雾火焰标模算例对求解器进行测试验证,之后对实际航空发动机折流燃烧室进行了两种工况下的喷雾燃烧模拟,最后对有关现象和结论进行了总结．

1 模 型 介 绍

1.1 湍流模型

经过LES过滤后的质量和动量方程如下:

(1)

表1 液相引起的源项表达式

1.2 燃烧模型

由于强烈化学源项的存在,直接在燃烧模拟中求解刚性极大的组分输运方程很困难,通常需要非常小的时间步长．FGM方法通过将所有燃烧相关参数映射到混合分数Z和归一化进程变量C的空间中,避免了这一情况．首先使用开源工具包Cantera求解一系列准一维稳态层流对冲火焰,在此过程中考虑详细的化学反应机理．混合分数Z采用Bilger等提出的表达式[20]．进程变量YC定义为主要生成物的线性组合YC=YCO2+YCO+YH2O．为了方便查表,进程变量被进一步归一化为

(2)

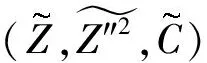
(3)

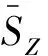
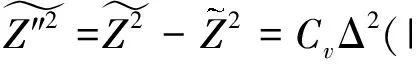
(4)

其中Cv设置为常数值0.15[21]．数值框架如图1所示．

图1 FGM方法的实施流程Fig. 1 Procedures of FGM method

1.3 液相模型

与纯气相燃烧不同的是液相在喷雾燃烧中起着重要作用．液滴演化由如下基本动力学方程决定:

(5)

∑Fi是作用在液滴上的总外力,可以使用如下表达式计算:

(6)

阻力系数CD由经验公式计算:

(7)

(8)

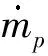
(9)

其中Sh是Sherwood数,Dab是蒸气质量扩散系数,BM是Spalding传质系数．

1.4 蒸发热损失模型

传统的FPV方法只适用于纯气相燃烧．对于喷雾燃烧,FPV的主要缺点是无法考虑液滴蒸发带来的热损失,进而导致温度预测值偏高．针对这一问题目前主要有四种处理方法:第一种方法是建表过程直接对准一维对冲喷雾火焰进行计算[15-16],但是这引入了与液滴相关的各种参数,包括液滴直径、液滴速度和液滴与空气的混合比,极大地增加了建表的复杂性．喷雾火焰面中混合分数的非单调性是另一个需要特殊处理的问题．第二种方法是对现有的气相表进行修正．其中最常用的一种修正方法是通过改变氧化剂侧的温度来量化液滴蒸发的影响[12]．这种方法需要引入一个新的控制变量,即混合物的绝对焓．这种方法虽然比较容易实现,但是目前仅适用于氧化剂侧温度较高的燃烧条件,例如温和或强烈低氧稀释(moderate or intense low oxygen dilution,MILD)燃烧．第三种方法不显式地引入液滴,而是通过经验公式将蒸发源项与一些已知的变量相关联,然后将此项包含在准一维喷雾火焰面计算中[18]．然而这种方法仍处于开发阶段,缺乏普遍性．第四种方法并不改变建表过程,而是在三维模拟中求解绝对焓方程,然后先查得各组分质量分数,再逆向求解温度,数值效率在一定程度上无法保证[23]．本文采用了一种更简单的,考虑蒸发热损失的方法,同样忽略了液滴蒸发对组分质量分数的影响[11],但需要在计算过程中对焓值进行如式(10)所示的修正,即从显焓hs中减去燃料潜热Lv和混合分数Z的乘积:

Δhs=-LvZ．

(10)

这一处理方法虽然是简化处理,但部分反应了蒸发和燃烧的相互作用,即在局部高温区,蒸发会导致焓值降低．这一焓差和当地的燃料总量成比例(假设当地燃料都由蒸发产生)．在下一节中将对这种扣焓处理的非绝热方法的预测性能进行评估．

2 标 模 验 证

2.1 实验配置

悉尼乙醇喷雾火焰 EtF7具有最高的载气流量并且接近火焰吹灭极限,因此被选为标准算例来验证该求解器[1]．悉尼燃烧器由同心排列的射流喷嘴、引燃器和空气伴流组成．用于雾化液体燃料的超声波雾化器位于射流出口平面上游215 mm处．生成的喷雾液滴通过直径为10.5 mm的管道输送,射流出口处的平均速度为60 m/s,化学恰当的乙炔/氢气/空气混合物用作引燃物以稳定火焰．引燃气体的平均速度为11.6 m/s,外径为25 mm,绝热温度为2 493 K;空气伴流的平均速度为4.5 m/s,其直径为104 mm．液滴动力学数据包括液滴尺寸分布和各方向液滴速度,由激光Doppler测速仪和相位Doppler研究风速测定法(LDV/PDA)测量．

2.2 数值设置

图2中直径为200 mm、长度为368 mm 的圆柱计算域被离散化为168万个六面体单元,在中心线附近进行了加密．中心线附近的网格分布如图3所示．另外在在下游x/D>20处对网格的轴向分布进行了疏化处理(网格数减半),用于检验结果对网格的敏感依赖性．为了代表完全燃烧状态,化学恰当混合分数取0.1,绝热温度取2 493 K,零混合分数变化和最大进程变量被设置为引燃入口边界条件．A实验组在第一个测量位置x/D=0.3的实验数据用于设置喷雾和气体进口条件．LEMOS湍流发生器用于产生入口湍流[24]．基于Lagrange-Euler框架的压力基LES-FGM喷雾燃烧求解器由OpenFOAM-v2012开源库中的SprayFoam求解器改进开发而成．PIMPLE算法用于压力速度耦合．

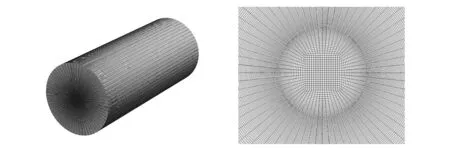
图2 悉尼喷雾燃烧室计算域及网格 图3 中心线附近网格分布Fig. 2 The computation domain and mesh of Fig. 3 Grid distribution near the centerline the Sydney spray combustor

2.3 反应流算例结果

先使用不同网格预测得到在轴向位置x/D=30处的气相平均温度、液滴Sauter平均直径(Smd)、液滴轴向平均速度的径向分布,如图4所示．虽然该算例计算结果对于网格的存在一定的依赖性,但两者差异相对较小,之后的结果展示中均选取细网格的计算结果．选取某轴截面,瞬时和平均速度模值、温度和混合分数分布如图5所示．在图5(a)、5(c)和5(e)中可以看到瞬时场呈现出明显的非稳态流动特征,而平均场类似于RANS的模拟结果．燃烧模拟的精度在很大程度上取决于流场预测的准确性,因为对流项在混合分数和进程变量的演化过程中起着重要作用．图5(f)中的平均混合分数分布表明在中心线附近燃烧处于富燃状态,该处的蒸发热损失不容忽视．在图5(d)中可以观察到该区域的平均温度较低．

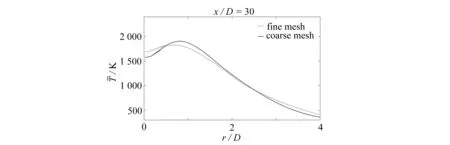
图4 不同网格预测得到在轴向位置x/D=30处的气相平均温度液滴Sauter平均直径Smd和液滴轴向平均速度的径向分布Fig. 4 Predicted radial profiles of mean gas temperature Sauter mean droplet diameter Smd and axial mean droplet velocity at x/D=30 with different meshes

(a) 瞬时速度场U (b) 平均速度场(a) Instantaneous velocity distribution U(b) Mean velocity distribution

考虑和不考虑蒸发热损失(在后文中分别记为FGMminusT和FGM)预测得到的平均气体温度在不同轴向位置x/D=10,20,30的径向分布如图6所示．图中还绘制了实验数据与Yi等[15]和Hu等[16]的喷雾火焰面模型预测结果用于比较．结果表明,简单地减去与当地混合分数成正比的温度值是提高喷雾燃烧模拟准确度的有效方法,特别是对于温度预测．FGMminusT和FGM两者位于富燃区的最大温度差异超过100 K．在三个轴向位置,实验测得的平均气体温度均沿径向先升高后下降．FGMminusT和FGM都很好地捕捉到了这种变化趋势．在x/D=10处,即使是FGM的结果也优于两个喷雾火焰面模型的结果．这种现象可归因于流场预测的不准确性．在x/D=20和x/D=30处,两个喷雾火焰面模型的结果略好于FGMminusT．我们注意到,所有方法均倾向于高估远离中心线的温度．这可能是由不适当的湍流-化学反应相互作用模型导致的,预设的PDF可能需要进一步改进．模拟结果和测量数据之间的偏差也有可能来源于实验误差．

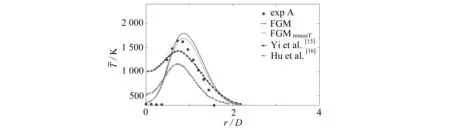
(a) x/D=10

FGMminusT预测得到的液滴Sauter平均直径(Smd)在不同轴向位置的径向分布如图7所示．两个实验集的数据和Yi等[15]的预测结果也绘制出来用于比较．FGM的结果与FGMminusT几乎相同,因此未在图中显示．结果表明,在所有轴向位置,当r/D<0.5时,FGMminusT的预测结果不如喷雾火焰面模型准确．但这种方法得到的Smd径向分布较为均一,比较类似于实验数据的趋势．而喷雾火焰面模型的预测Smd,在r/D>0.5时,沿径向不断减小并且与实验值的误差增加．这可能是因为在在这个径向范围内,喷雾火焰面模型的预测温度低于实验值．小液滴的蒸发量少于预期,因此它们的体积分数会增加．

从实验值中还可以注意到,测得的Smd沿轴向方向缓慢增加,这是由于小液滴的沿程蒸发．然而,在预测结果中没有观察到这种趋势．

FGMminusT得到的液滴轴向平均速度在不同轴向位置的径向分布如图8所示．

两个实验集的数据和Yi等[15]的预测结果也被绘制出来用于比较．可以发现FGMminusT的结果显著优于喷雾火焰面模型,尤其是当x/D>20时．这一现象表明,简单的火焰面模型可能并不会降低对液滴统计数据的预测性能．合适的入口边界设置和流场的准确预测更为重要．

总的来说,简单地减去一个温度值的非绝热FGM方法(FGMminusT)在气体温度和液滴统计数据预测方面与喷雾火焰面模型的性能相当．

3 实际折流燃烧室模拟

3.1 问题描述

应用该求解器在真实的航空发动机折流燃烧室上进行数值模拟．表2中列出了两组工况的具体参数．总压损失通过测压耙测定,其中出口总压由于存在径向梯度,因此在出口截面沿周向布置四处测压耙,每个测压耙沿径向均布5个测点进而得到该截面处平均总压．工况1具有较低的空燃比和较低的工作压力．对1/3燃烧室进行建模仿真,其几何结构如图9所示．涡轮导向叶片也包含在计算域内．该计算域用310万个四面体单元进行离散,局部网格见图10．在空气入口设定固定质量流量边界条件．液体燃料(图9中的红点)从火焰筒内壁面上的狭槽喷入．所有的壁面均设置为无滑移绝热边界．出口处给定固定压力均值边界条件．

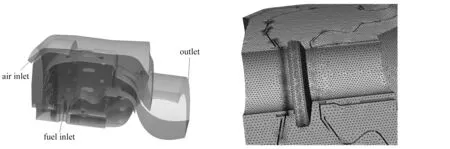
图9 实际折流燃烧室的计算域 图10 计算域网格的局部几何细节Fig. 9 The computation domain of the realistic Fig. 10 Local geometric details of the computation mesh slinger combustor

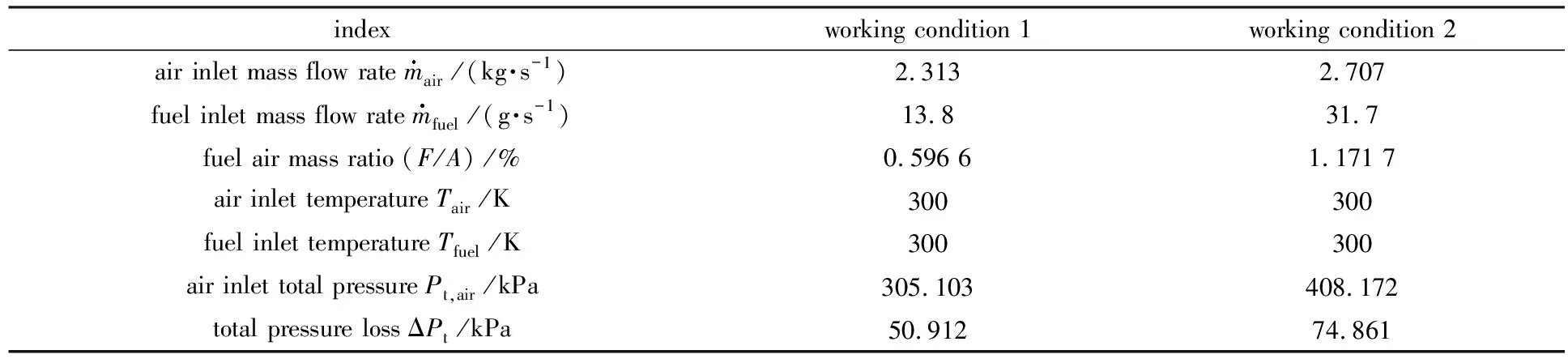
表2 两组不同工况的测量数据

选择正十二烷作为航空煤油的替代燃料,并使用经过详细化学反应机理和实验数据验证的具有54种组分的骨架化学反应机理[25]来生成FGM表．初始燃油雾化粒径的平均值根据如下的经验关系式[26]进行数值估算:

(11)

并且假定其服从Rosin-Rammler分布,其中n为甩油盘转速(30 000 r/min),R为甩油盘油孔出口处的半径(159.7 mm)．为了进一步简化模拟,假设初始液滴径向速度等于切向速度,液滴从整个狭槽面连续喷入火焰筒内．数值模拟过程中时间项离散选择Euler隐式格式,扩散项离散选择二阶中心格式,对流项离散选择一阶迎风格式,最大Courant数设置为0.5．

3.2 结果与讨论

两种工况在y=0截面的预测瞬时速度分布和流线图如图11所示．可以看到在这两种工况下,气流通过导向叶片时均被极大加速．从流线图中可以看出,从主燃孔进入火焰筒内的气体在两种工况下具有完全不同的轨迹．工况2中该气流主要偏向右侧,而工况1中很大一部分会偏向左侧．这背后的原因是工况2的入口燃料空气比较高,燃烧时形成了较大的火焰区．

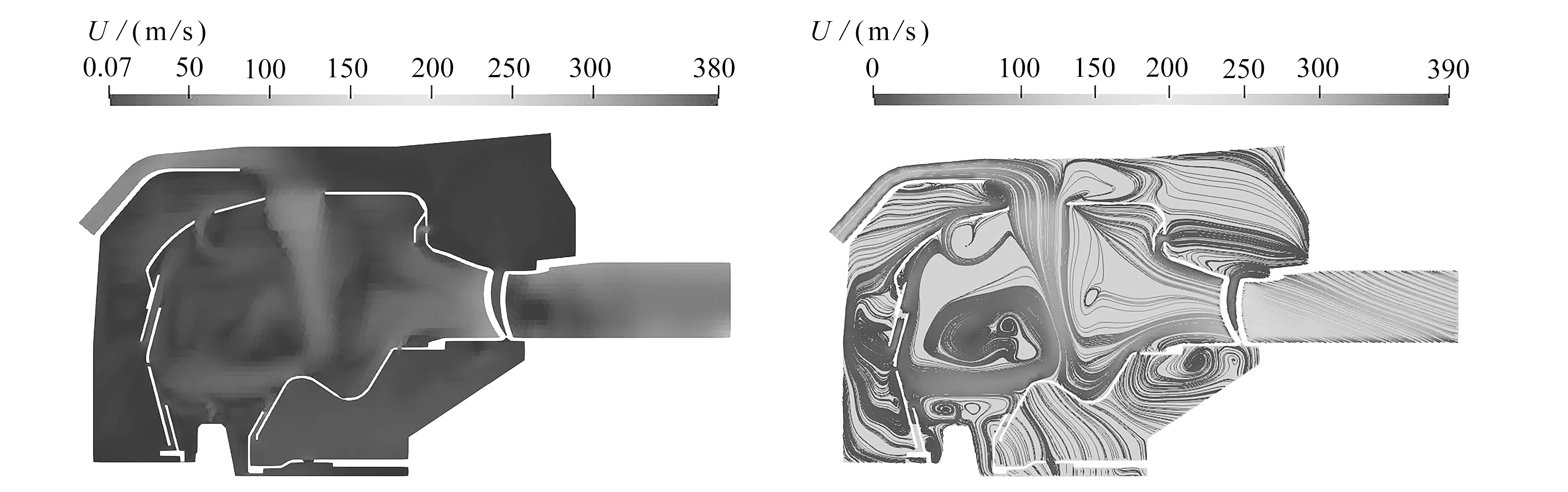
(a) 工况1瞬时速度 (b) 工况1流线图(a) The predicted velocity distribution of working condition 1 (b) Streamlines lines of working condition 1

两种工况在y=0截面的预测瞬时和平均总温分布如图12所示．从瞬时场中可以看到,燃烧在工况2中更稳定,而在工况1中,尽管存在大块悬浮火焰,但根部火焰几乎在此时被吹灭．工况1的平均总温分布也更加不对称,因为燃烧反应速率要小得多,主流和来自火焰筒内壁面的流动的影响更大．工况2中导向叶片前存在较大的高温区,在实际运行时应当避免．

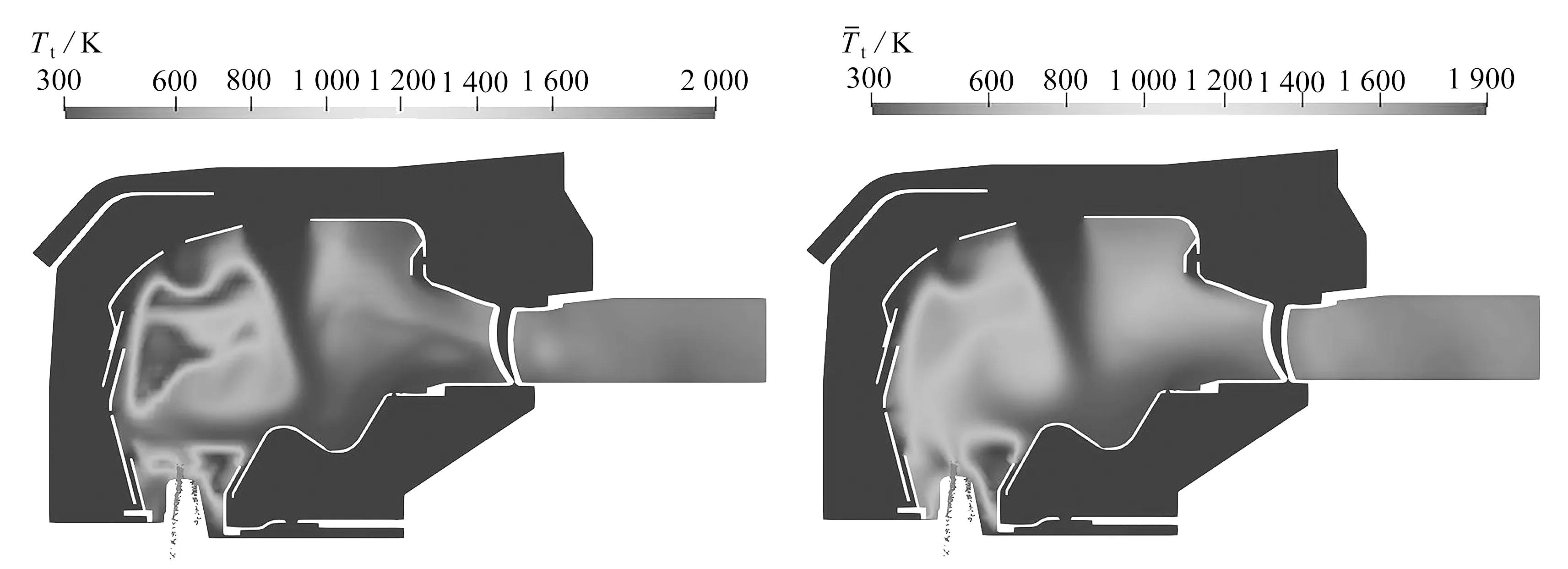
(a) 工况1瞬时总温 (b) 工况1平均总温(a) The predicted instantaneous total temperature (b) The mean temperature distribution of distribution of working condition 1 working condition 1

图13给出了两种工况下,在涡轮导向叶片后缘后方17 mm处截面的预测瞬时和平均总温分布．可以看到,工况1中该截面的总温比工况2低得多,正对应了该工况下较低的燃料空气比．值得一提的是,对于这两种情况,该截面处预测的平均混合分数均略高于入口处的混合分数,这说明平均而言该处的燃料与空气已掺混均匀,与预期一致．但瞬时场显示较大的温度梯度仍然存在．

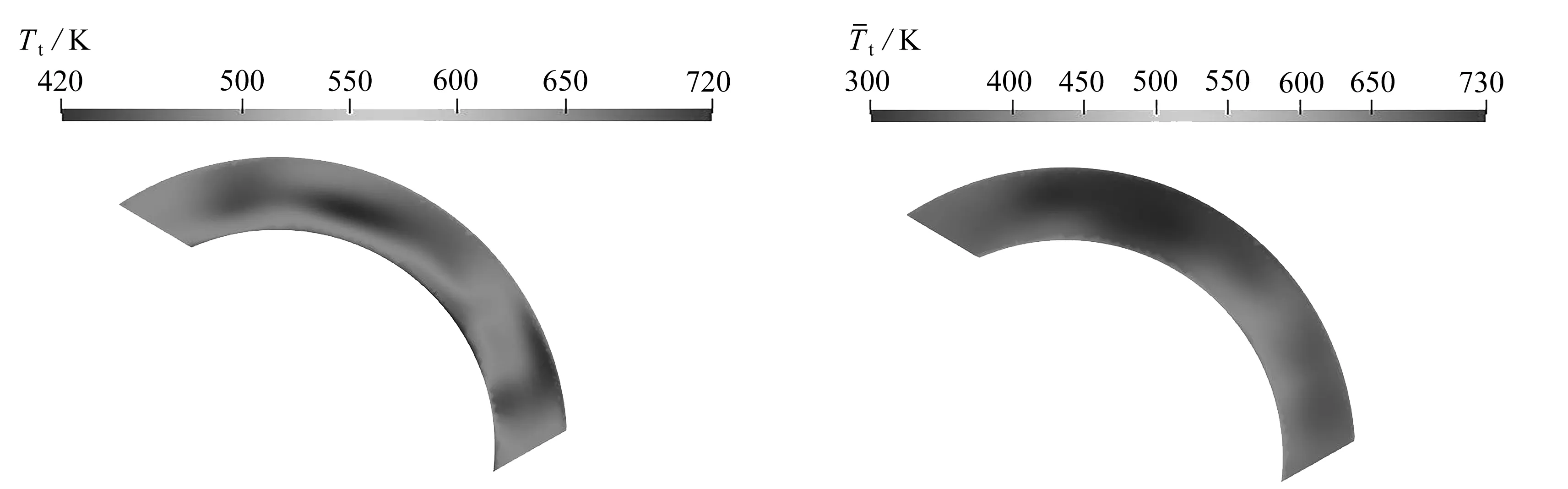
(a) 工况1瞬时总温 (b) 工况1平均总温(a) The predicted instantaneous total temperature (b) The mean temperature distribution of distribution of working condition 1 working condition 1

燃烧组织形式的更多细节可以由Takeno火焰指数ξ定量刻画．ξ的具体定义为

(12)

其中YF为燃油质量分数,YO为氧气质量分数,ξ=+1表示预混模式,ξ=-1表示非预混模式．两种工况下,在y=0截面的火焰指数分布如图14所示．火焰筒外部的火焰指数可以忽略,因为该处燃料的质量分数几乎为零．观察可知,由于更高的入口燃料空气比,工况2进油口附近由于蒸发起主导作用而产生的预混区要比工况1大得多．蒸发的燃料在燃烧前与周围的空气混合．两种工况下非预混燃烧都是主要燃烧方式．预混区主要由湍流混合形成,但不起主导作用．两个燃烧区中进程变量源项的条件均值见表3．可以看到,在这两种工况下,平均而言非预混燃烧都更加强烈,尽管工况1中两种燃烧模式的差异较小．

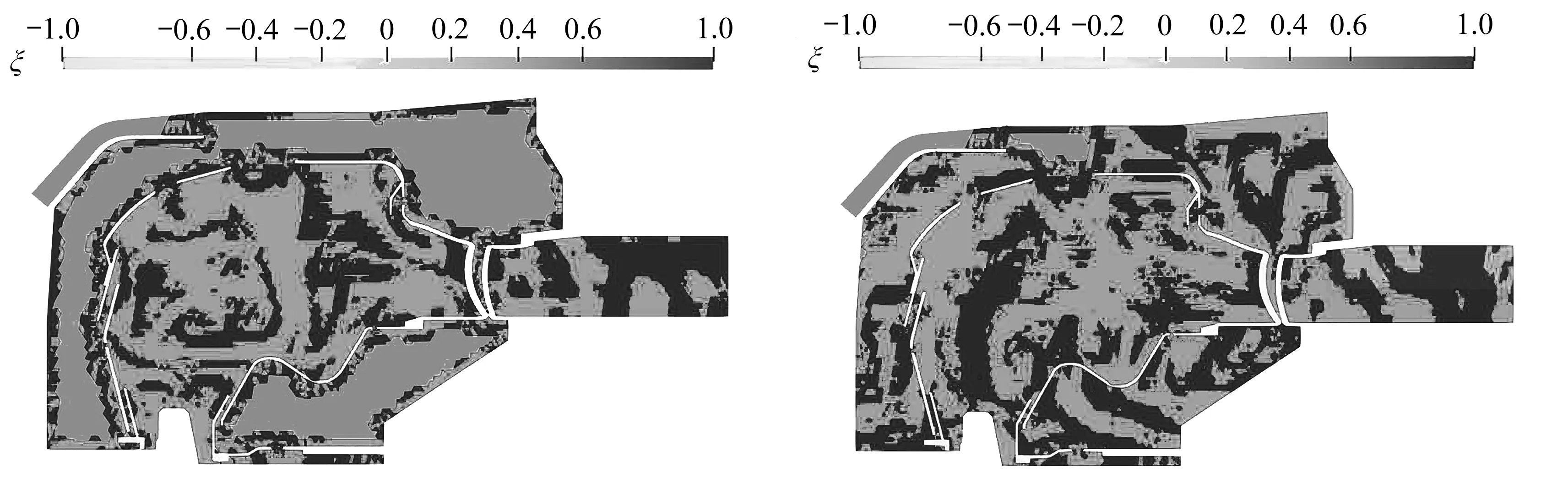
(a) 工况1 (b) 工况2(a) Working condition 1 (b) Working condition 2图14 y=0截面的预测火焰指数分布Fig. 14 Predicted flame index distributions at section y=0

表3 进程变量源项在不同燃烧区域的条件均值

两种工况的预测总压力损失分别为49.282 kPa和77.547 kPa．这与表2中的测量值较为吻合．偏差小于3.5%．

4 总 结

LES-FGM喷雾燃烧求解器针对悉尼乙醇喷雾火焰EtF7进行开发和验证．蒸发热损失通过简单地减去与当地混合分数成正比的温度值来考虑．气相温度与液滴统计数据预测结果与实验值较为接近,基本可以实现与喷雾火焰面模型相当的预测性能．湍流与化学反应相互作用建模可能是当前误差的主要来源．

该求解器又被用来模拟真实的航空发动机折流燃烧器在两个工况下的喷雾燃烧情况．模拟结果合理地捕捉了这两种工况之间的差异,并且预测得到的总压损失接近于测量值．进一步提高喷雾燃烧模拟性能的方法包括求解输运PDF方程来更准确地模拟湍流-化学反应相互作用与通过引入和能量相关的控制变量来考虑壁面或辐射带来的热损失．