基于变密度胞元的热传导结构层级拓扑优化*

王 钦, 刘利阳, 强 博, 魏衍强

(沈阳飞机设计研究所, 沈阳 110035)

0 引 言

低温环境是确保电子设备、发动机、航天飞机和卫星等系统安全工作的必要条件之一．因此,结构散热一直以来都是学者和工程师研究和设计的热点[1]．其中,热传导系统具有加工简单、不依赖其他电子系统、无噪声等优点,在工业应用中最为广泛．随着设备精度的不断提升,研究微型化、轻量化、高效化的散热系统至关重要．

拓扑优化是一种新型的结构优化设计方法,其不依赖于工程经验就能得到意想不到的创新构型,被广泛应用于基于热传导、热对流和共轭传热的热系统优化[2-3]．然而,这些研究大多只是在宏观尺度上进行结构优化,设计空间有限．在自然界中,植物茎和动物骨骼等生物结构多是由胞元结构组成,具有高刚度、耐腐蚀、多功能和轻量化等优越的性能[4]．受这一现象的启发,结构的宏观和微观一体化拓扑优化设计受到了研究者们的关注．

多尺度拓扑优化设计可以追溯到Rodrigues等[5]提出的宏观尺度材料分布和微结构设计协同优化的层级算法．Xia和Breitkopf[6-7]将非线性FE2框架应用于多尺度设计．然而,这些设计中每个单元的微结构都不同,计算成本高,且难以制造．为此,Liu和Cheng等[8-9]提出了一种并行拓扑优化方法来设计周期胞元结构,只需求解一个简单的优化公式,大幅缩减了计算成本．Long等[10]将这种方法应用于考虑承载能力和保温性能的结构轻量化设计．Yan和Huang等[11]解决了以宏观结构刚度和材料导热系数为目标函数的多目标多尺度结构优化问题．Yan等[12]证实,对于热弹性问题,周期胞元结构比宏观结构表现出更好的性能．但由于微观结构相同,设计空间有限,只能获得很小的性能改进．

变密度胞元结构[13]是另一种特殊类型的多尺度结构,其微结构具有相似的拓扑结构,仅一个或多个几何参数在宏观设计域内变化．通过优化这些几何参数,可以将不同密度的微结构置于最佳宏观位置．Wang等[14]通过优化不同六边形单胞的厚度,使结构的散热效率提高一倍．Cheng等[15-16]开发了一种网格密度填充和与设计相关的动态特征的并行优化方法．Wu等[17]开发了一种考虑尺度效应的带惩罚的简化子结构近似(ARSP)模型．然而,在这些工作中,微观结构拓扑是规定的,而不是优化得到的．

在微观结构拓扑与宏观密度并行优化中,最困难的是如何提取一个参数来改变微结构的密度．特别是在拓扑优化框架中,用元素密度或水平集函数描述微观结构拓扑,很难提取一个显式的参数,如半径或厚度．最近,基于水平集框架,Wang等[18-19]提出了一种在不同位置切割带符号的距离函数的参数化方法．在此基础上,Zong等[20]为保证相邻单元之间完美的几何连接,通过插值一组位于节点上的高度变量,构造了一个可变切割函数．而后,一种类似的形状插值技术被提出来生成一系列基于参数水平集方法优化的微结构[21-22]．

本文提出了一种实现微观结构拓扑与宏观密度并行拓扑设计的有效方法．首先,在密度框架下优化具有不同体积分数的单一或有限种微结构;然后应用腐蚀-扩散算子构建准周期微结构库;最后,解决宏观热柔顺度最小问题,并将这些微结构置于宏观设计域．

1 优 化 模 型

1.1 变密度胞元结构

图1为典型的变密度胞元结构,其微结构密度ρ由内孔半径R控制．由于微结构拓扑是预定的,性能改进有限．文献中有很多性能优异的微结构拓扑优化构型[23-27],但其复杂的几何结构导致很难提取一个显式的几何参数来改变密度．

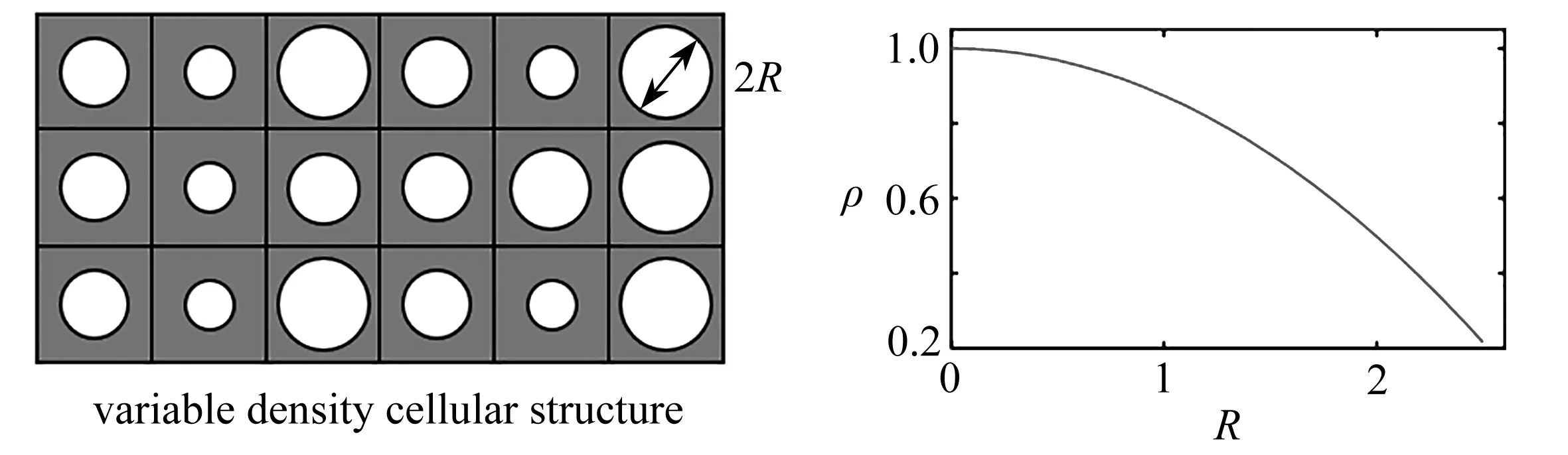
图1 变密度胞元结构及其几何参数与密度的关系Fig. 1 Illustration of the variable density cellular structure

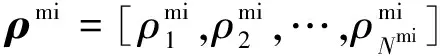
(1)

(2)

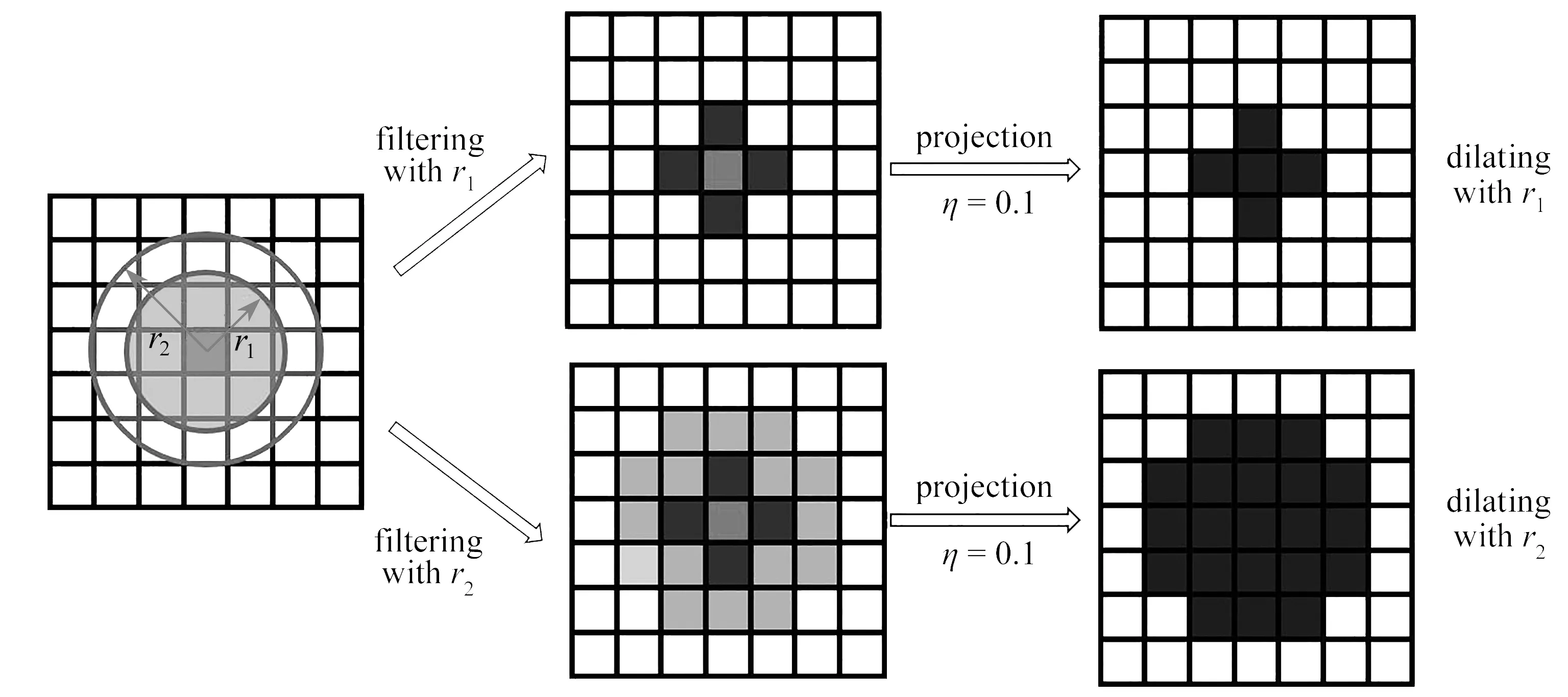
图2 腐蚀-扩散算子Fig. 2 The process of the “erode” and “dilate” operators

1.2 优化流程

为了更清楚地说明本文提出的算法,本小节给出了热对流问题微观结构拓扑与宏观密度分布并行拓扑设计的具体优化流程,如图3所示．

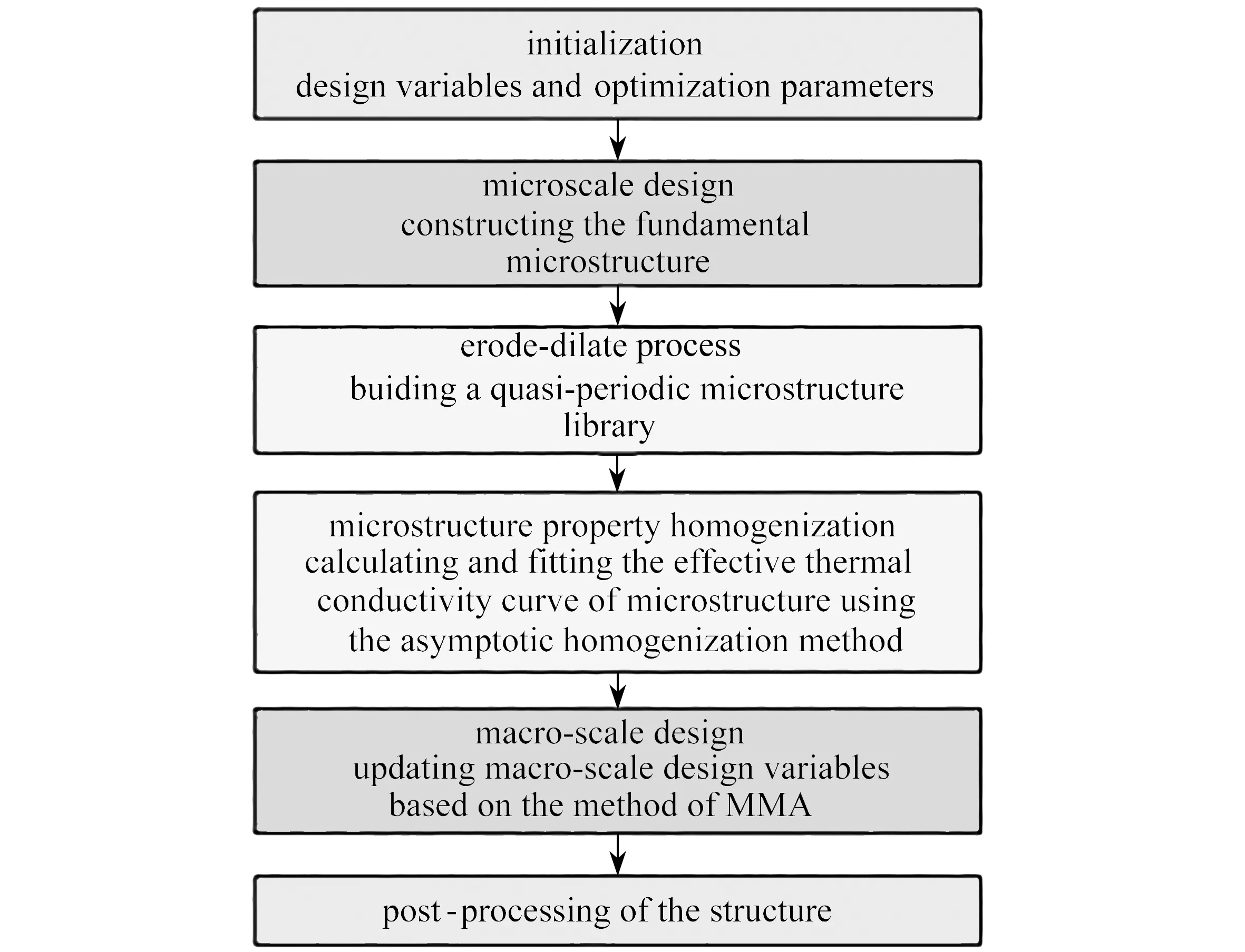
图3 提出算法的优化流程图Fig. 3 The optimization flowchart of the proposed method

Step 1: 优化得到有限个体积分数不同的微结构;

Step 2: 基于腐蚀-扩散算子,建立准周期微结构库;

Step 3: 利用渐近均匀化方法计算微结构等效材料属性,及其B样条代理模型;

Step 4: 优化宏观单元的密度分布;

Step 5: 基于MMA 优化算法更新设计变量,完成结构优化并进行后处理及验证．

2 问 题 描 述

本节针对热传导问题验证本文算法的有效性,测试模型设计域为边长L=1 m的正方形,均布热载荷Q=1 W/m2．规定左侧中部长度为L/10的边界T=0 K,其他边界对流系数为0(图4)．

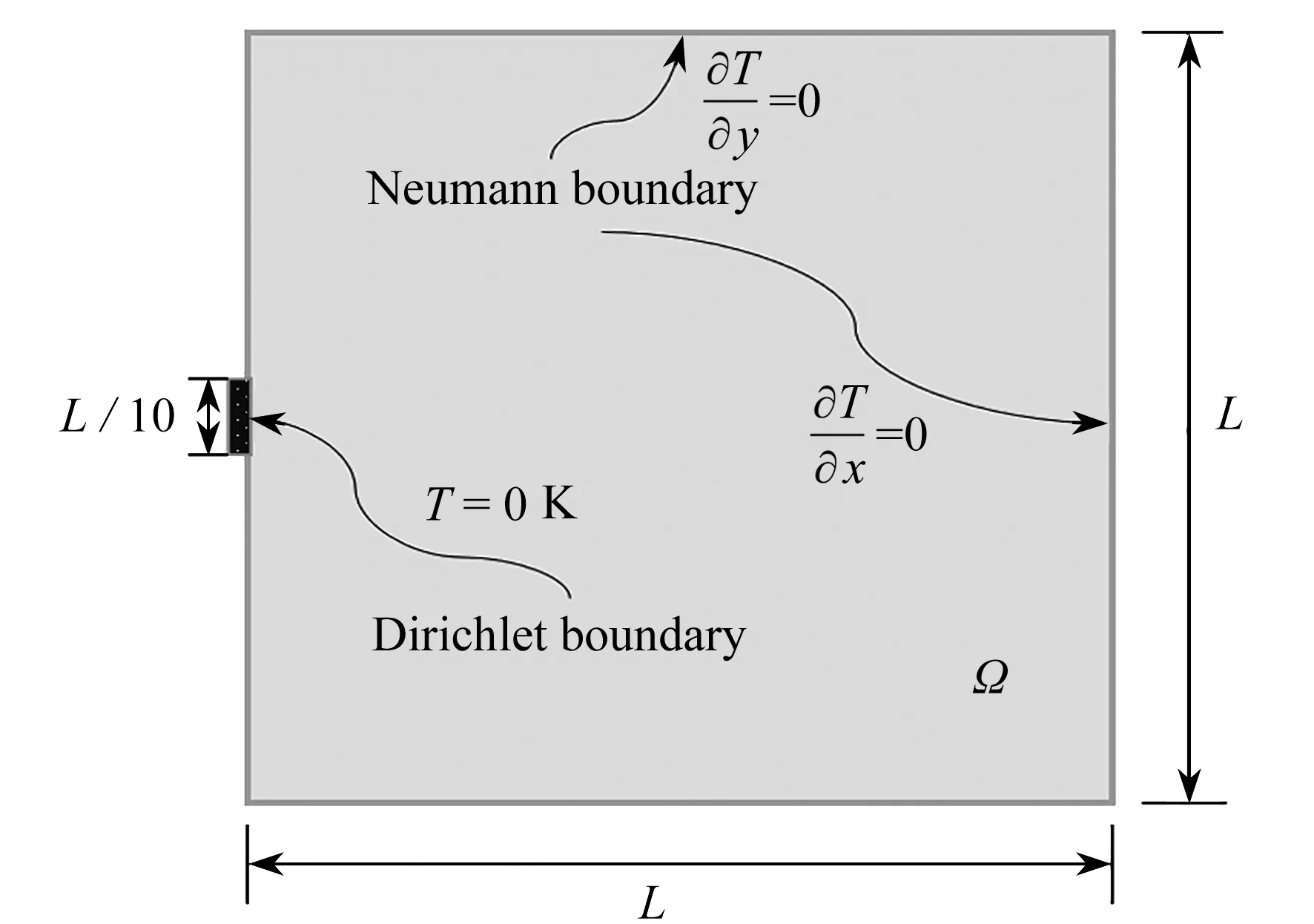
图4 设计域及边界条件Fig. 4 The design domain and boundary conditions

网格划分规模为100×100．为提高结构热导率,优化采用双材料,其导热系数分别为k1=1 W/(m2·K)和k2=0.001 W/(m2·K)．

在稳态热传导问题中,结构热柔顺度被广泛用于性能评估．结构的热柔顺度值越小,说明结构的导热性越好．因此,本文考虑了体积约束下结构热柔顺度最小的优化问题:

J=TTKT,

(3)

其中,K和T分别表示全局热传导矩阵和温度向量,满足方程KT=Q,Q为热载荷向量．矩阵K可由下式计算得到:

(4)

其中,Ωe和Nma分别表示单元积分域和单元个数,B是单元应变矩阵,De是位于第e个宏观单元的微结构的等效热传导系数矩阵．

本文基于渐近均匀化方法[29]计算微结构的等效矩阵:

(5)

其中,D(y)是微观材料插值得到的热传导系数矩阵,y代表微观积分域,εy(·)是应变算子,φ=[φ11,φ22,φ12] 代表求解施加周期性边界条件的均匀化问题得到的三个特征位移场:

(6)

其中,Vy={uy(y)|y∈Y,uy(y+Y)=uy(y)}表示单元Y中定义的周期函数的函数空间,v表示虚位移场．

3 微观尺度设计

3.1 微观尺度优化模型

基于密度的拓扑优化方法,采用均匀化方法和MMA优化方法进行微观结构设计:

(7)

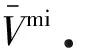
(8)

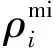
(9)

其中

(10)

且

(11)

3.2 微结构拓扑优化结果

1) 策略1:不考虑微结构之间的连通性

对体积分数分别为0.2,0.4,0.6,0.8的优化公式(7)求解,可以得到如图5所示的4种微观结构．本文将这些微观结构称为“基础微结构”．

图5 基础微结构(策略1)Fig. 5 The elementary microstructure for strategy 1

为保证经腐蚀和扩散后的微结构具有光滑边界,对微结构进行网格细化,将每个微观单元划分为nc×nc的细网格,如图6所示．本文选择nc=3,将微结构的网格细化为240×240．

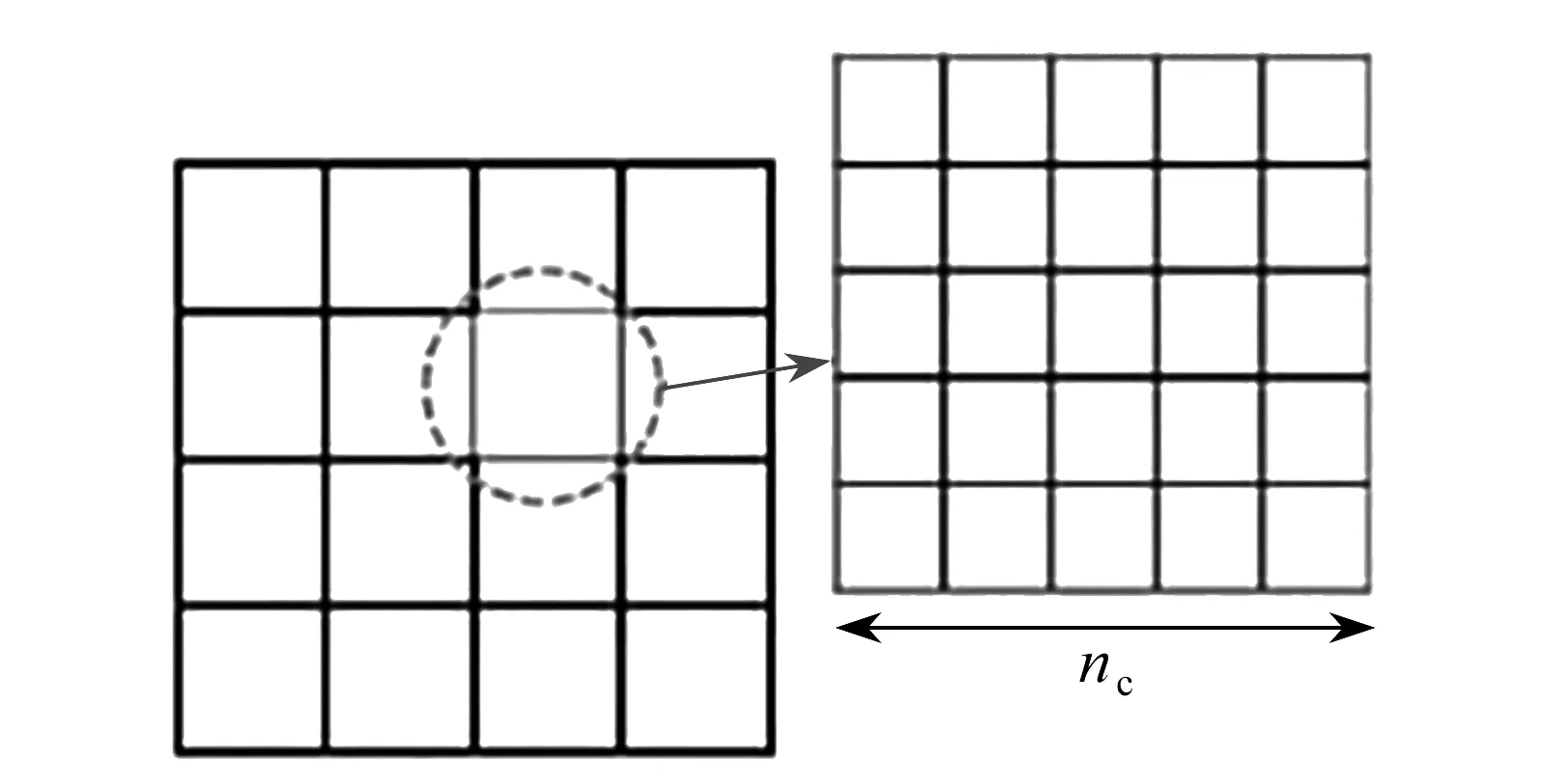
图6 网格细化示意图Fig. 6 Mesh refinement

利用腐蚀-扩散算子,可以得到一系列密度从0至1变化的微结构,参数设置如下:过滤半径设为rmin=8.6,β值固定为128,微结构体积分数从0.05至1变化,间隔为0.05(共20步),从而得到4×20个微结构,并选择若干体积分数均匀增大的微结构作为准周期微结构库①,用于后续的计算和优化,如图7所示．

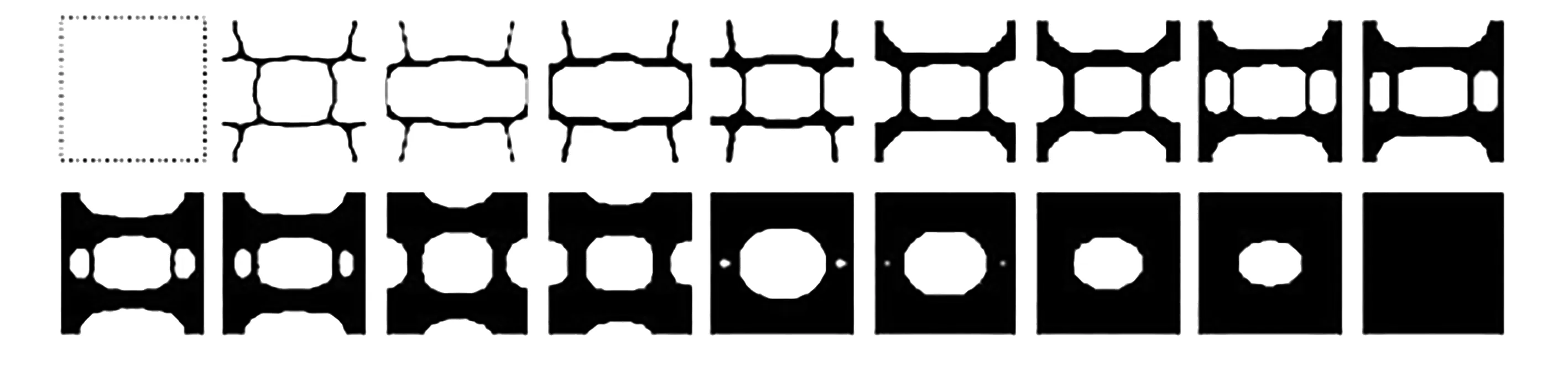
图7 准周期微结构库①Fig. 7 The microstructural library ①

2) 策略2: 考虑微结构之间的连通性

由于策略1中不同体积分数的微结构拓扑是独立计算的,微结构间的连通性较差．本文将体积分数较小的微结构作为不可设计域,依次优化获取体积分数较大的微结构．首先,优化得到体积分数为0.2的微结构,并作为不可设计域优化体积分数为0.4的微结构,同理,优化得到体积分数为0.6和0.8的微结构．从而得到4个连通性较好的基础微结构,如图8所示．应用策略1中的腐蚀-扩散算子,得到准周期微结构库②,如图9所示．

图8 基础微结构(策略2)Fig. 8 The elementary microstructure for strategy 2

图9 准周期微结构库②Fig. 9 Microstructural library ②

4 宏观尺度设计

4.1 等效材料属性

基于渐进均匀化法计算两组准周期微结构等效矩阵DH,

(12)

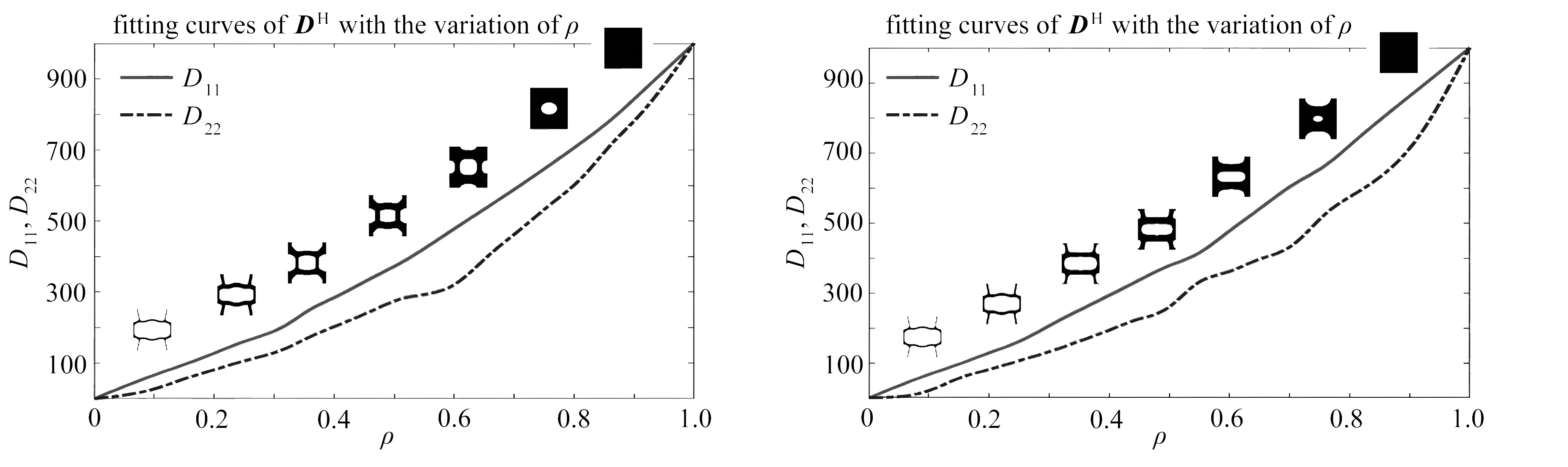
(a) 准周期微结构库① (b) 准周期微结构库②(a) Microstructural library ① (b) Microstructural library ②图10 等效热传导系数曲线Fig. 10 Fitting curves of D11 and D22 with the variation of

4.2 宏观结构优化结果

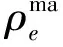
(13)

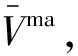
(14)

其中,下标e=1,2,…,Nma．迭代过程如图11所示．准周期微结构库①和准周期微结构库②的优化结构热柔顺度分别为31.279 3和30.252 6．考虑连通性的结果值略小于不考虑连通性的结果值．

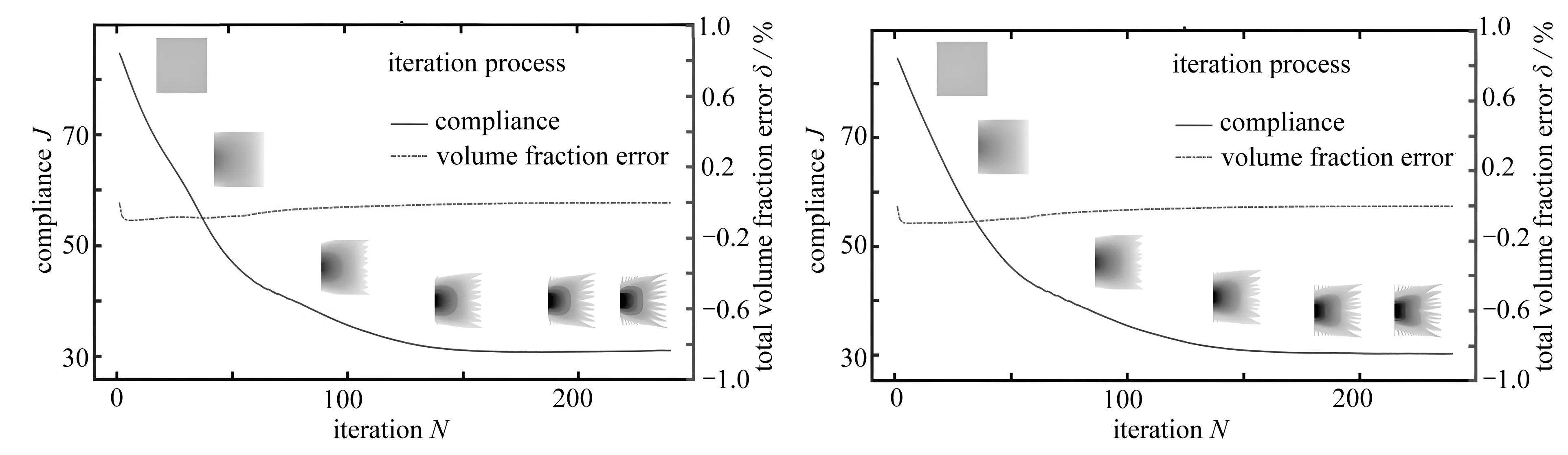
(a) 准周期微结构库① (b) 准周期微结构库②(a) Microstructural library ① (b) Microstructural library ②图11 迭代过程Fig. 11 The iteration process of example 1

4.3 变密度胞元结构组装

宏观优化完成后,利用体积分数最接近的微结构对各个宏观单元进行组装,得到变密度胞元结构,如图12所示．

(a) 准周期微结构库① (b) 准周期微结构库②(a) Microstructural library ①(b) Microstructural library ②图12 优化结果Fig. 12 The optimized structures for different methods

5 比较与验证

在本节中,引入了另外两个方案验证方法的有效性．方案一选择体积分数0.2的微结构拓扑优化结果作为唯一的基础微观结构,方案二为单一宏观尺度设计．为了消除均匀化带来的误差,验证4种设计的性能,建立了4种设计的细网格模型,并计算了温度场．

5.1 两种对照方案

1) 单一基础微结构

方案一 选择体积分数为0.2的微结构作为单一基础微结构,经腐蚀、扩散,得到一个微结构族．由于只有一个基础微结构,需要大的过滤半径来获得具有大体积分数的微结构,产生高额计算成本．因此,我们调整了腐蚀-扩散策略:过滤半径设置为8.5,η=0.8和η=0.2分别实现腐蚀和扩散过程,从而得到两种微结构．对新的微结构继续应用腐蚀-扩散,重复这个过程,建立准周期微结构库③,如图13所示．图14为等效材料属性拟合曲线,图15为宏观区域密度分布．优化后结构的热柔顺度为31.393 1．

图13 准周期微结构库③Fig. 13 Microstructural library ③

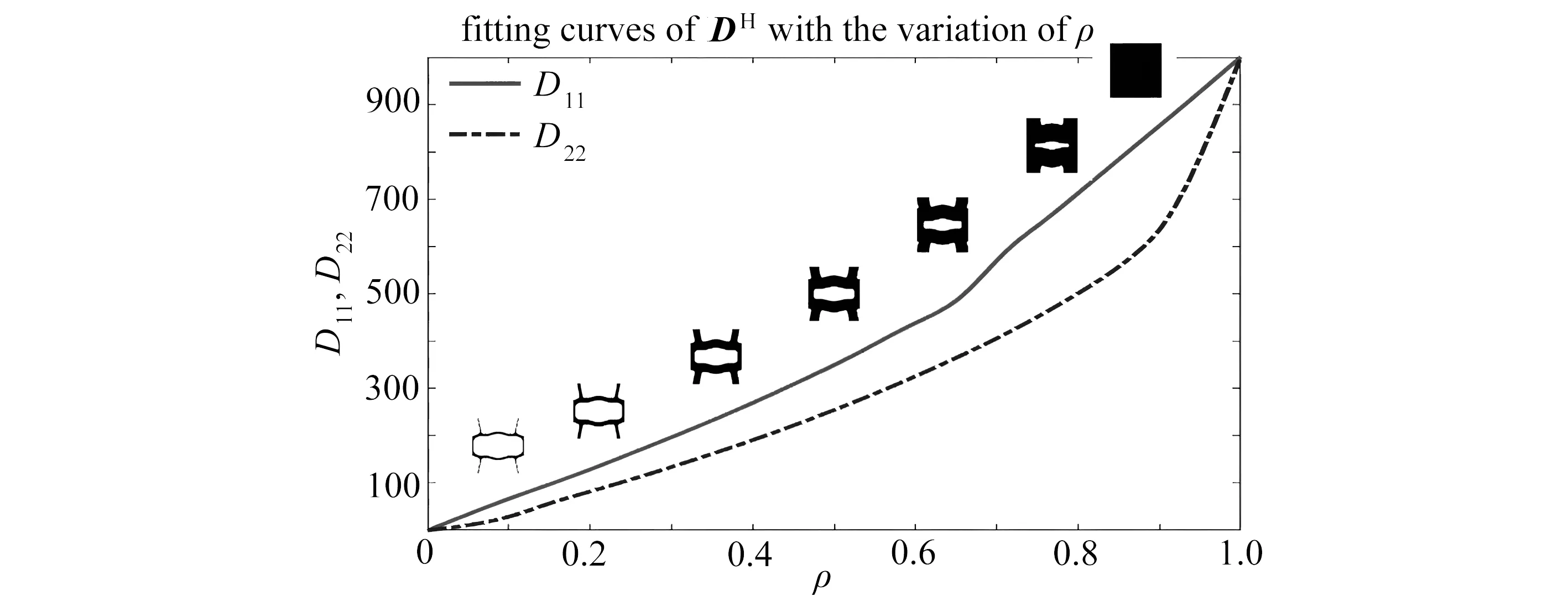
图14 准周期微结构库③的等效热传导系数曲线Fig. 14 Fitting curves of D11 and D22 with the variation of in library ③

图15 准周期微结构库③的优化结果Fig. 15 The optimized structures for library ③

2) 宏观单尺度设计

方案二 给出了宏观单尺度设计,以说明引入双尺度设计对结构性能的提升．优化模型及参数与文献[32]相同．拓扑优化结果如图16所示,热柔顺度为48.162 9．

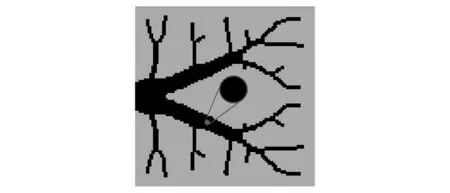
图16 宏观单尺度拓扑优化结果Fig. 16 The topology optimization result of the single macro-scale design

5.2 方案验证

在拓扑优化过程中,采用渐近均匀化方法计算等效材料性质,并假定周期边界,忽略非均匀性和非连通性．为了准确评定4种结果的散热性能,采用8 000×8 000的精细网格离散优化结果．优化后结构的温度场如图17所示．计算温度场的一系列参数,用于后续对比,如表1所示．

表1 不同策略优化结果的结构散热性能

图17 精细网格下的温度场优化结果Fig. 17 Temperature fields of the 4 optimization results with the fine mesh

结果表明,变密度胞元结构比传统的宏观优化结构具有更好的热性能．相比之下,其热柔顺度等参数明显降低．在准周期微结构库①中,由于在微结构优化时没有加入不可设计域,导致一些微结构之间的连通性较弱,结构性能下降．准周期微结构库③的构建只使用了体积分数为0.2的微结构,扩散得到体积分数较大的微结构与最佳微结构存在偏差,其散热性能也降低了．此外,4种优化方案的最终结构体积分数分别为0.202 5,0.201 7,0.200 4和0.200 7．体积分数偏差小,在允许范围内．因此,本文提出的变密度多尺度拓扑优化方法是合理的,优化后的结构散热性能优异．

6 结 论

本文将变密度多尺度拓扑优化方法应用于散热结构优化．基于腐蚀-扩散算子处理基础微结构生成准周期微结构库．采用渐进均匀化方法计算微结构的等效热传导系数,得到拟合曲线,用于宏观优化,并组装变密度胞元结构．此外,由于相邻微结构共享相似的微结构拓扑,具有较好的连通性．数值算例表明,与传统的宏观尺度设计相比,变密度结构具有更好的散热性能．