圭表测距
——从初中物理第一课说起
欧建文 熊 慧 朱昌勇
(韶关学院智能工程学院物理系,广东 韶关 512005)
物理学是一门注重实验的科学,也是一门崇尚理性、重视逻辑推理的科学,它充分将逻辑性强的数学推理作为工作用语,探索发现自然界的奥秘. 广袤的星空为物理学提供了天然的实验室,很多自然规律都来自于对星空的观测和测量. 中学物理第一课就涉及到了最基础的长度测量,好奇的学生可能在不经意间会问出“太阳距离我们有多远?”这样的问题.
依靠先进的科技,对当代人来说这是一个常识;但是在科技落后的古代,它却是个惊天之谜. 根据成书于公元前一世纪左右的《周髀算经》记载,我国古代数学家陈子对太阳的距离进行了测量.[1,2]
1 圭表测太阳高度
陈子在东周都城洛阳一带立了一个八尺高的圭表,如图1.[3]圭表是测量日影长度的天文仪器,由“圭”和“表”两个部件组成. 垂直于地面的直杆叫作“表”;水平放置于地面上,带有刻度用以测量影长的标尺叫作“圭”. 陈子在夏至这一天,用圭表测量到了日影长一尺六寸,并以此为基点,在正南方向一千里的地方,测量到表影长一尺五寸;而在正北方向一千里,日影长一尺七寸. 测量太阳高度的方法,原理如图2所示.S表示太阳,AB和CD是相隔一定距离的两个圭表,在同一时刻测量日影的长度,再利用几何知识可以推算出太阳的高度.

图1 圭表
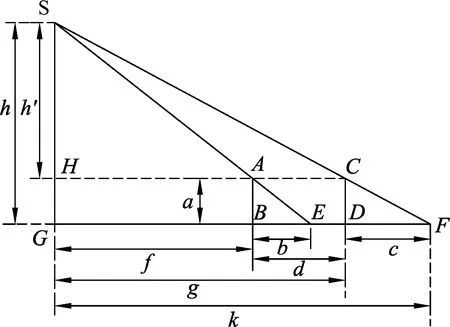
图2 圭表测太阳高度示意图
方法1:设太阳高度SG=h千里,GF=k千里,圭表高度AB=CD=a千里,圭表一日影长BE=b千里,圭表二日影长DF=c千里,两圭表距离BD=d千里. 计算矩形ABDC的面积为
矩形ABDC的面积也可以直接算得S▭ABDC=AB·BD=ad.
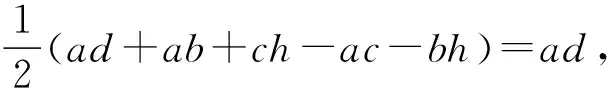
得ab-ac+ch-bh=ad.
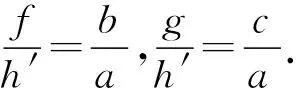
得到
h′=fa/b.
(1)
h′=ga/c.
(2)

所以
(3)
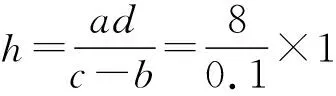
2 圭表测地球周长
局限于天圆地方的古代哲学思想,古人认为地球是平的,在天与地是平行平面的基本假设下提出太阳高度的测量原理. 现在,我们改变地球是平的基本假设,视地球是圆的,同样利用圭表测日影的方法,经过简单的几何推导,可以测量地球的周长,见示意图3.

图3 圭表测量地球周长
太阳距离地球非常遥远,阳光几乎是平行传播到地球,在洛阳测得太阳光与圭表之间的夹角∠1,洛阳往北一千里测得夹角∠2,通过平行关系得∠1′=∠1,∠3=∠4. 所以,两地与地心连线之间的夹角等于两地圭表测得的太阳高度角之差:∠4=∠3=∠2-∠1′=∠2-∠1.
在洛阳,八尺长的圭表,日影长度是一尺六,太阳高度角的正切值为8/1.6,对应的角度为78.6901°;洛阳往北一千里,日影长度变长到一尺七,太阳高度角的正切值为8/1.7,对应的角度为78.0031°;两地太阳高度角之差为0.6870°,该角度的大小正比于从洛阳到正北方一千里地方的那部分地球的周长为
因此,地球周长为524.04千里. 注意:古代的千里与现代千里不同. 在不同的时期,古代长度度量单位的数值也是不一样的,李德鲁通过比对北回归线与洛阳的距离,指出《周髀算经》的一里约为77米.[4]因此,524.04千里相当于现在的40351 km. 由圭表最后得到的地球周长为40351 km,与现在用轨道航天器精确测量的地球周长值40070 km,相差0.7%. 利用简单的几何和基本的科学推理,更改下天圆地方的观念,就可以利用两千多年前的圭表测日方法,测量出了精度在1%以内的地球周长.
3 结语
根据观测和严密的逻辑推理,人们就能测量出整个地球的大小——这是中华传统科技的魅力,也是物理学科的魅力. 随着科技的进步,除了本文介绍的几何方法外,还有更多的先进方法用于天体测量中. 地球大小的测量与地图绘制、卫星定位等生产生活信息息息相关,其测量精度也不断提高. 教师在教学过程中可鼓励学生积极探索多种多样的测量方法,不断探索教学新方式、新方法.

