多无人机路径规划下冲模型*

陈立军

（广州软件学院，广州 510990）

0 引言

多无人机（multi-UAV）路径规划是近几十年来的一个热门研究课题，它应用广泛，如侦察应用、编队飞行应用，甚至娱乐应用［1-3］。多无人机路径规划问题的一个关键要求是所有无人机都能在不发生碰撞的情况下，成功地从初始位置飞行到指定目标。

许多路径规划研究都针对现有算法在不同方面面临一些问题，如通过富障碍物环境的导航、计算效率和解的最优性［4-6］，然而，很少有人研究无人机下冲效应。下冲效应是指无人机旋翼下由于大量的气流而产生的诱导力，从而获得向上的升力。下冲效应会让无人机失去稳定性，与邻近的无人机相撞，或坠毁到地面等。下冲力是真实的多无人机实验中一个不可忽视的问题，特别是在三维密集的环境中。

强烈的下冲气流会导致下方无人机失去稳定性，改变姿态，下降高度；弱下冲气流对无人机的影响很小，下冲气流的强度取决于转子旋转速度和行进距离，因为气流速度与转子旋转速率成正比；并且空气在行进时扩散，如果下冲效应强度是可获得的，则无人机由于下冲而引起的行为将是可预测的。一些文献提出了获得下冲气流强度的方法：YEO等在四旋翼上实施了压力探头流量测量系统［7］，以感测下冲气流速度，但这种方法需要无人机安装额外的仪器来收集下冲效应数据，并在获得下冲气流数据之前承受下冲效应，当无人机收集数据并预测气流是有害时，它们已无法作出及时反应来避免下冲气流。

为了从路径规划的角度解决下冲问题，无人机可以使用避免碰撞的方式避开这个不安全的垂直区域。HÖNIG 等将无人机建模为轴对齐的椭球体［8-9］，FERRERA 等将无人机建模为圆柱体，椭圆形和圆柱形都允许无人机扩大其垂直距离，因为路径规划算法会防止建模形状被碰撞［10］。图1 展示了通常的球形无人机模型，圆柱形模型为紫色，下冲气流为黄色。

图1 无人机模型Fig.1 UAV model

然而，避免碰撞的额外空间会导致路径规划算法性能降低，在避免下冲和性能之间需要权衡。在考虑圆柱形状时，体积的大小和高度很重要，圆柱体高度需要足够高，这样无人机不会在垂直方向上相互靠近，并且施加在下方无人机上的下冲力是微不足道的，因为下冲力会随着垂直距离的增加而减小。然而，圆柱体太高可能会对性能产生负面影响，例如，由于无人机体积的增加，所有无人机到达所需位置的过渡时间都会增加，额外的体积也意味着其需要一个额外的区域让两架无人机互相绕行（避开）。目前所知，现有的工作没有确定无人机几何参数的规则，也没有详细研究这些几何特性对多无人机路径规划的影响。

本文开发了一种下冲模型，可以预测无人机的下冲效果，而无需在无人机上安装任何额外的仪器，下冲模型将给出下冲力和垂直距离之间的关系。受下冲效应影响的无人机的姿态和位置将能够从下冲模型中确定，采用成群结队算法（flock）和最优交互避碰算法（optimal reciprocal collision avoidance，ORCA）来测试下冲模型［11-12］，并针对圆柱形无人机模型进行定制，对比分析了不同算法和不同模型在有效下冲作用下的性能。

1 下冲模型

当多架无人机在3D 密集环境中飞行时，下冲效应可能会很严重，要将下冲力考虑到多无人机路径规划算法中，需要知道下冲效应对远处无人机的影响有多大。

本章推导出一个下冲模型，用于在没有任何附加传感器帮助的情况下，预测四旋翼无人机的下冲效果，该推导利用无人机加速度来获得下冲力。从四旋翼的一般运动方程开始，从加速度获得无人机推力。根据动量定理，利用无人机推力来获得转子引起的气流速度，应用射流概念来获得距离与气流速度之间的关系，气流速度转换为下冲力。将无人机姿态和扭矩纳入下冲模型，假设四旋翼无人机是同质的（现实中，无人机编队也是同型号的无人机），这意味着所有无人机都具有相同的重量和尺寸，从顶视图看，无人机也被假定为圆形（本文建议的就是圆柱形，从上往下看就是圆形），并且始终为零偏航角。

下页表1 是本文使用的参数或名称。

表1 参数或名称Table 1 Parameters or names

1.1 下冲力模型

下冲力是由于大量的气流产生升力而产生的，升力与无人机的推力直接相关，所要求的推力大小取决于所需的加速度，假设有合适的控制器算法可用，加速度可由惯性测量单元（IMU）传感器或路径规划算法的命令获得，由四旋翼无人机的运动方程可以得到推力与加速度的关系，无人机的运动方程可以表示为：

其中，m 为四旋翼的质量；X=［x，y，z］T为无人机在惯性系统中的位置；为惯性力；RIB为旋转矩阵；T为沿其本体框架z 方向的推力，g 为重力加速度，使用加速度输入，推力可通过式（1）确定，如下所示：

其中，I3=［0，0，1）T，假设4 个转子之间产生的推力相等，则一个转子产生的推力为Tr=T/4。

推力是由转子旋转产生的气流产生的，转子旋转得越快，转子下方的气流速度越快，推力越大，推力（Tr）和诱导速度（wi）之间的关系与零自由流速度假设如下：

其中，ρair为空气密度，Arotor为转子扫过的面积；合成气流速度Vi的方向与推力Tr相同，沿无人机机身框架z 轴的负方向。

气流散开并随着距离的增加而减速，位于产生下冲力的无人机下方且垂直远离无人机的受下冲效应的影响较小，因此，需要求得气流速度与距离的关系。射流概念给出了气流速度与距离之间的关系［14］，因此，在下冲模型推导中采用，假设气流速度在水平面上是均匀的并且最大，则相对于垂直距离（z）的气流速度表示为V（z），图2 显示了上述步骤。

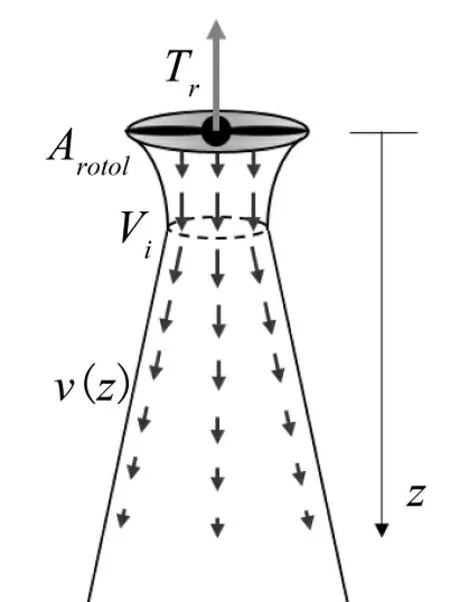
图2 转子下方的气流Fig.2 Airflow under the rotor

当气流撞击一个表面时，会施加一个力，因此，对于距离上层无人机较远的无人机，其所施加的下冲力可以通过将气流速度转换为力来计算，让（xtop，ytop，ztop）和（xbot，ybot，zbot）分别是顶部和底部无人机的位置。假设扩散气流可以忽略不计（此时建议无人机编队在出发前要选择晴朗无大风的天气），因此，当顶部无人机在z 轴上与其重叠时，底部无人机将受到下冲力的影响，这种重叠也可以表示为（xtopxbot）2+（ytop-ybot）2<=ruav，其中，ruav是无人机的半径，假设来自所有4 个转子的混合气流不影响最大气流速度（无人机出发前选择好天气，是可以这样假设的），并且气流速度在给定z 的xy 平面上是均匀的，还假设下冲气流不影响无人机推力和螺旋桨（一般情况下冲气流不会影响到无人机的推力和螺旋桨），在给定垂直距离差（z=ztop-zbot）的情况下，作用在底部无人机上的下冲力和加速度如下：

1.2 下冲效应

下冲气流方向沿无人机机身框架z 轴负方向，因此，随着无人机的滚动和俯仰，下冲气流改变其方向，遭受下冲的下部无人机不仅遭受垂直力，而且还遭受水平力。此外，如果气流的中心没有碰到无人机的重心，就会产生感应扭矩，本节推导出下冲气流方向及其对下部无人机的影响，还介绍了下冲气流对诱导扭矩的推导，随着下冲气流方向的改变，可能遭受下冲的下层无人机将被重新定义。在极少数情况下，位于顶部无人机正下方的下部无人机可能不会遭受下冲，而与顶部无人机水平距离的下部无人机可能会遭受下冲，这一切都取决于顶部无人机的位置和状态。

为了确定无人机是否会受到下冲力的影响，应该判断其是否会被任何下冲气流击中，如果从顶部无人机的机身框架角度来看，若其低于顶部无人机，将受到下冲力的影响，因此，两架无人机相对于顶部无人机机身框架的位置是判断的关键，两架无人机UAV1 和UAV2 之间的位置关系可以描述如下：

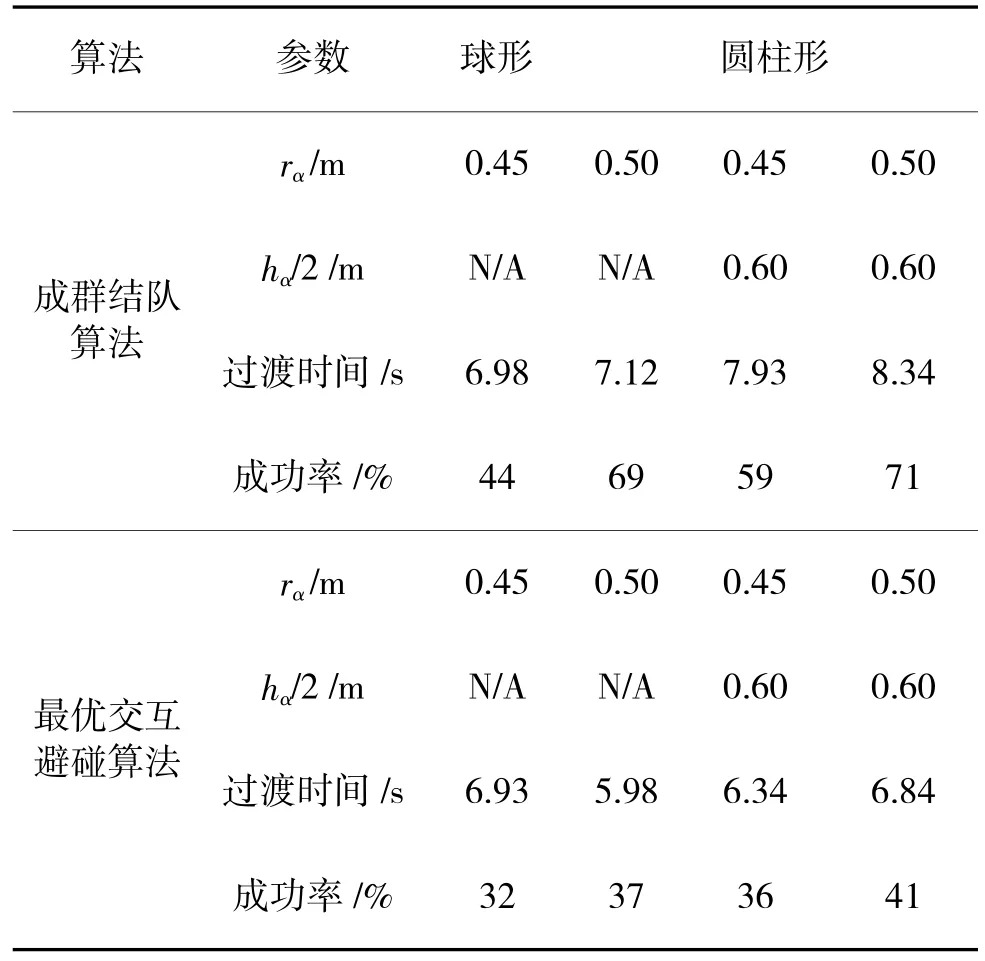
其中，p1，p2

下冲气流方向沿UAV1 的负z 轴方向，因此，从UAV1 的角度来看，UAV2 正在遭受以下下冲加速：

从初始帧来看，下冲效果是让UAV2 减速的方向：

在上一节中，仅考虑下冲力/加速度，如果气流撞击无人机的重心是正确的，那么，通常情况并非如此，例如下冲气流只撞击底部无人机的边缘，无人机不仅接收到下冲力，还接收到扭矩，导致额外的侧倾或俯仰，本节推导出由于下冲气流而施加在无人机上的扭矩量，考虑基本扭矩方程：

如果下冲力的中心施加在无人机机身框架的x轴或y 轴附近，则扭矩可以直接考虑到俯仰角或侧倾角。但是，如果下冲力的中心没有施加在x 轴或y轴附近，则无人机俯仰角和侧倾角会同时受到影响。

在图3 中，假设两者方向相同且UAV2 在UAV1 下方，虚线所示圆圈为UAV1 产生的下冲气流，和是式（8）中的值，绿点是下冲力中心施加的点，而是指绿点所在位置的角度。

图3 UAV1 机身框架中气流区域和底部无人机的俯视图Fig.3 Top view of the airflow area in the UAV1 fuselage frame and the bottom UAV

2 路径规划算法

路径规划算法允许一组无人机从其初始位置行进到最终位置而不会发生碰撞，在本文中，路径规划问题假设以下场景：

1）有n 架无人机在三维环境中飞行；

2）每架无人机都有唯一的初始位置和唯一的最终位置；

3）每架无人机都受到最大允许速度的限制；4）环境中没有障碍物，因此，只有无人机间的碰撞需要注意。

2.1 成群结队的算法

本节介绍了成群结队算法（又称鸟群算法），这是一种受一群鸟集体行为启发的算法，这群鸟有一个共同的目标，它们相互靠近飞行，但很少发生碰撞。REYNOLDS 首次模拟了鸟群行为，他提出了3个规则：避免碰撞、速度匹配和鸟群中心化，这些规则表明，个体应避免与邻居拥挤，以邻居的平均速度移动，并以邻居的平均方向引导［14］；OLFATI 根据REYNOLDS 的3 条规则，提出了一套数学背景和理论框架的鸟群算法，每只鸟被3 个基于力的条款控制：导航反馈、基于梯度的条款和速度共识条款，导航反馈将鸟引向目标，基于梯度的条款由吸引力和排斥力组成，试图使所有鸟的相对距离保持在选定的距离附近，速度共识项试图保持所有鸟具有相同的速度［15］。

SEMNANI 等将OLFATI 的数学工作修改为适用于多无人机的路径规划［11］，其中，每架无人机都有一个独特的目标，取消了速度共识项，因为无人机不需要匹配速度，修改了基于梯度的项，仅由排斥力组成，因为每架无人机都有自己的目标，但仍需避免相互碰撞，导航反馈是不修改的，无人机动力学和作用在单个无人机i 上的力（f）的数学表达式如下：

当无人机被建模为圆柱体时，两个无人机的水平距离差在交互半径rα以内，且其姿态差在交互高度hα的一半以内时，被认为在彼此的交互区域内，在式（19）、式（20）中提出的宿主UAV的成群结队算法排斥力，通过增加高度差约束来说明圆柱体高度hα的情况。

2.2 ORCA 算法

ORCA 算法是一种基于速度的算法，该算法是为多无人机导航问题设计的，它是第一个能够保证大量无人机在密集环境中进行局部无碰撞运动的算法［12］。

在ORCA 算法中，每架无人机在假设其他无人机作出类似行为推理的基础上采取行动，每架无人机都知道其他无人机的信息，如位置、速度和半径，一架无人机利用其他无人机的信息，在一个时间范围内（）进行预测，并获得一组速度，如果选择这些速度，在时间之前会导致无人机间的碰撞。因此，在这种速度约束下，该算法通过基于无人机的最佳速度计算ORCA 半平面来优化性能，当无人机被认为是圆柱体时，圆柱体高度hα也被用来确定ORCA半平面。

一架无人机将为其他每架无人机获得一个ORCA 半平面，所有ORCA 半平面的交点（）是无人机可以选择的速度集，并保证在时间内无碰撞，新的速度将是中最接近首选速度的速度，首选速度是引导无人机走向目标的速度［13-14］。

2.3 总结

对于这两种算法，每一架无人机都不需要相互通信，并且有完美的感应，这意味着一架无人机能够推断出环境中的障碍物和其他无人机的确切形状、位置和速度，它们被设计用来解决多无人机运动规划问题，并保证在密集的环境中无碰撞［15-16］。一方面，成群结队算法是一种基于力的方法，目标诱导出一个吸引力，附近的无人机诱导出排斥力，由此产生的力是不受限制的，所以无人机的速度指令可能在一个时间步长内从最大允许速度Vmax变为最小允许速度Vmin。另一方面，最优交互避碰（ORCA）算法是一种基于速度的算法，保证时间内无碰撞，为了防止成群结队算法引起的速度跳跃，在导航反馈力和排斥力的作用下，使用了一个加速度限制器amax和排斥力的结果。

3 仿真结果

3.1 下冲模型仿真结果

当底部无人机悬停而顶部无人机从其上方飞行时，会发生最严重的下冲效应，这种情况最大化了底部无人机遭受下冲气流的时间。因此，为了测试下冲模型，顶部无人机从（0，1，1.8）飞到（2，1，1.8），底部无人机悬停在（1，1，1.5），采用了文献［16］中的简单无人机动力学，最大允许的滚动和俯仰角为0.3 rad。成群结队算法的导航反馈用于无人机移动到其想要的位置，使用的参数为：时间步长t=0.01 s，最大允许速度Vmax=1.5 m/s，导航反馈参数c1=7 和c2=9。图4 显示了底部无人机在遭受3 种不同下冲情况时的位置，第1 种情况是不考虑倾斜下冲效应（图4a），第2 种情况是不考虑下冲扭矩（图4b），第3 种情况是考虑整个下冲模型（图4c）。在第1 种情况下，底部无人机仅受到向下的力，被推下1.29 m；在第2 种情况下，由于倾斜的下冲气流，底部无人机向下行进0.97 m，水平行进1.12 m，在这种情况下，无人机行进的垂直距离小于第1 种情况，因为水平运动使无人机受到垂直下冲力的影响较小；在第3 种情况下，底部无人机向下移动0.91 m，水平移动1.06 m，无人机的水平运动小于第2 种情况，因为下冲扭矩与倾斜的下冲力相反，顶部无人机从其初始位置移动到所需位置需要2.88 s，完成第1 种、第2 种、第3种情况分别需要3.56 s、3.35 s、3.29 s。

图4 底部无人机的位置Fig.4 Location of the bottom UAV

3.2 有效下冲效应的路径规划算法仿真结果

对所提出的下冲力模型进行了模拟，以观察下冲力如何影响无人机的状态，以及圆柱形无人机模型如何有利于路径规划算法，成群结队算法和ORCA 都已经成功地在二维和三维环境中进行了编码、执行和模拟，提出ORCA 算法的研究小组在网上提供了开源代码［17］，对文献［17］进行了修改，以考虑到圆柱形无人机模型。

为了比较成群结队算法和最优交互避碰算法的性能，具有相同功能的算法中的参数被设置为相同的值，这些参数是：交互半径rα；交互高度hα；无人机的半径ruav=0.15 m；时间步长Δt=0.15 s；ruav=0.15 m；时间步长Δt=0.01 s，以及最大允许速度Vmax=1.5 m/s。仅用于成群结队算法的参数是：最大允许加速度amax=5.0 m/s2，排斥梯度ρ=1 000，以及导航反馈参数c1=7 和c2=9。用于最优交互避碰算法的时间跨度被设定为rα/Vmax。

为了比较球形和圆柱形无人机模型在具有下冲效应的三维密集环境下的性能，模拟环境设置为10 架无人机在一个宽2 m、长2 m、高1 m 的空间内盘旋，10 架无人机从这个空间的一侧飞到另一侧。这10 个无人机的初始和目标位置是随机产生的，表2 显示了球形和圆柱形无人机模型的过渡时间性能和100 个结果的平均成功率，用于成群结队和最优交互避碰算法，过渡时间是所有无人机从初始位置到目标位置的总时间，这个值越大，性能越差，无人机模型的效率越低。成功率是指无人机成功到达目标而没有被碰撞或卡住的次数，这个值越高越好。如表2 所示，当球形和圆柱形模型具有相同的半径时，圆柱形模型的性能具有更高的成功率，这一结论得到了成群结队算法和最优交互避碰算法的支持，可以证明圆柱形模型可以防止无人机因下冲效应而发生碰撞。最优交互避碰算法与成群结队算法相比，成功率较低，因为它在计算下一个速度时考虑了其当前的速度，并逐渐改变速度，无人机将不能足够快地避开附近的无人机。对于成群结队算法的结果，其验证了交互区域越大，过渡时间越差，然而，最优交互避碰算法的情况并非如此，因为时间跨度会随着交互区域的变化而变化，交互区域的变化，算法规划无人机移动的时间也会变化。

表2 采用不同模型的路径规划算法的仿真结果Table 2 Simulation results of path planning algorithms with different models

4 结论

在本文中，开发了一种下冲模型，该模型可以在没有任何仪器帮助的情况下预测无人机上的下冲力。下冲模型包括确定下冲效果的大小和方向，可以预测对抗下冲气流的无人机的姿态和位置，模拟演示了无人机如何受到下冲效应的影响，修改了成群结队算法和最优互易避碰算法以考虑圆柱形无人机模型。仿真验证了圆柱模型在具有有效下冲力的3D 密集环境中提高了路径规划成功率。未来的考虑包括下冲模型和圆柱形无人机模型的改进。在下冲模型开发过程中进行了许多假设，因此，没有考虑许多要素，例如下冲气流撞击时螺旋桨的影响，下冲气流延迟、散布气流速度和气流速度4 个转子合并，这些是可以考虑改进下冲模型的一些要素。仿真结果表明，交互区域越大，时间性能越差，因此，可以开发一种具有平衡安全性和性能的方法。