基于改进免疫模拟退火算法的WTA 问题求解
闫锦鹏,郭俊文,刘 刚*,张 宾,周文婷,宋丽琼
(1.北方自动控制技术研究所,太原 030006;2.陆军装备部驻北京地区军事代表局驻太原地区第二军事代表室,太原 030006)
0 引言
空袭与防空是信息化战争的重要组成,如何在复杂的战场环境中建立高效的防空体系,提高地面防空武器系统的生存和作战能力,是地面防空所面临的实际而又紧迫的问题[1]。武器目标分配(weapon target assignment,WTA)问题是地面防空领域的经典问题之一,是解决如何将多个打击目标合理分配给多个甚至多种作战武器,以达到最大杀伤效果的问题[2]。
武器目标分配问题本质上是运筹学中的非线性多目标优化问题[3]。经过无数学者专家的研究,产生了众多解决WTA 问题的方法,比如数学规划、博弈论、马尔科夫决策、动态规划以及智能优化算法等[4-5]。传统的数学方法诸如数学规划、动态规划、遍历搜索等受限于计算速度,问题规模和其他一些因素,在解决WTA 问题时存在诸多局限。智能优化算法则由于其对目标函数要求低、适应性强等优点脱颖而出。
文献[6]于1990 年首次提出将遗传算法(genetic algorithm,GA)应用于求解WTA 问题。文献[7]采用带精英策略的快速非支配排序遗传算法(non-dominated sorting genetic algorithms,NSGA-Ⅱ)求解了海军舰艇编队的多目标WTA 问题。文献[8]应用多目标离散粒子群算法(discrete particle swarm optimization,DPSO)求解考量通信延迟和武器消耗条件下的水下对抗WTA 问题,设计改进了算法的粒子位置和速度更新公式,使求解方法符合问题的离散域特征。文献[9]针对WTA 问题,在标准模拟退火算法(simulated annealing,SA)的基础上融入禁忌搜索算法(tabu search,TS),重新构建了威胁函数并优化分配模型,提高了算法的搜索效率。
在采用传统单一的智能优化算法解决武器目标分配问题时,存在收敛速度慢、求解质量低、分配结果不合理的缺陷。综上所述,本文针对地面防空的WTA 问题,设计了弹炮结合武器系统打击无人机的防空作战案例,并提出一种结合免疫算法和模拟退火算法的改进算法,采用模拟退火思想中的Metropolis 准则更新抗体群,增加求解全局最优的能力,到算法搜索后期,温度下降,抛弃劣解进而加快收敛速度。将改进算法应用到WTA 模型中,验证有效性并求解分配问题。
1 武器目标分配模型分析
1.1 武器目标分配模型
假定N 个火力单元要对m 个目标进行火力打击,每个火力单元必须选择目标进行打击并且一次只能打击一个目标,每个目标可以由多个火力单元进行打击,并假定N 个火力单元的打击能力相同。火力分配的适应度函数可表示为f。
其中,ωj表示第j 批目标的威胁系数;pij表示第i 个火力单元对第j 批目标的毁伤概率为决策变量,表示第i 个火力单元是否对第j 个目标进行射击。xij=1,射击;xij=0,不射击。
1.2 约束条件
实战中防空武器的作战能力和作战效果会受到以下约束条件的限制。
1)空间条件约束。当目标处在某个火力单元的射程范围内,其需要分别满足火力单元在水平方向和竖直方向的拦截远近界,即满足:
式中,rmin为武器拦截近界;rmax为武器拦截远界;α为发射俯仰角;β 为发射方位角;H 为空袭目标在垂直方向上的距离;D 为空袭目标在水平方向上的距离。
2)时间条件约束。时间约束是指如果某个火力单元打击目标必须在固定的时间段[Ts,Td]内开始并完成,表示该任务具有时间条件约束。
3)资源约束。出于简化模型和求解问题的需要,还应设定以下的资源约束:
假定每个火力单元最多打击一个目标,即:
打击任务同时满足空间条件约束、时间条件约束和资源约束时,决策变量xij=1,可以进行射击;否则,xij=0,不射击。
2 模拟退火算法
2.1 模拟退火算法概述
1953 年,Metropolis 受物理退火的启发提出了模拟退火的思想[10],模拟退火算法的基本思想如下:设定初始解,借助于温度控制参数的变化产生新解,计算目标函数,利用Metropolis 准则判断是否接受新解,重复这个过程从而不断迭代,直到使得目标函数达到最优。
模拟退火算法的特点为:在模拟退火过程中,适当地控制温度的下降速度,在迭代过程中不仅能使目标函数优化,同时还能以一定的随温度下降而下降的概率接受使目标函数劣化的情况,所以模拟退火算法能实现跳出局部最优解,而获得目标函数对应的全局最优解。
2.2 模拟退火算法步骤
标准的模拟退火算法的基本步骤如下:
Step 1 初始化参数,包括初始温度T0,终止温度Te,更新函数中的冷却参数α,迭代次数L;
Step 2 随机生成一个初始解x0,在初始时刻,当前解xk就等于x0;
Step 3 将xk增加一个随机偏移量值,生成一个领域解x ;

Step 5 判断算法是否已经达到最大迭代次数L,如果已经达到,进入下一步,如果没有,返回Step 3;
Step 6 判断算法是否满足设定的终止条件,满足则输出最优解,若不满足,则利用温度更新函数更新当前温度,并返回Step 3。
模拟退火算法的构成要素如下:
1)初始温度:设定的初始温度越高,算法的搜索规模就越大,但是如果设定的初始温度过大,算法的迭代次数就会过多甚至超出限制,算法的效率也会变低[11]。因此,想要在理想时间内得到最优解,就需要设定恰当的初始温度。
2)温度更新函数:在模拟退火算法中,温度更新函数控制温度下降的速度。温度下降过快,则算法易陷入局部最优;而温度下降过慢,算法的收敛速度就会降低,从而降低算法的效率。
标准模拟退火算法的温度更新函数为:
3)迭代次数:设定好温度更新函数和温度后,迭代次数可以保证算法最终达到平衡状态。迭代次数过长或过短都会影响算法的效率,实际应用中,要根据问题规模的大小设定合适的迭代次数。
4)终止条件:①随机设定一个常数,当温度降到这个常数时,迭代停止。②算法迭代出最优解,迭代停止。③在迭代过程中陷入局部最优值,无法取得全局最优值,迭代停止。
3 基于免疫算法改进模拟退火算法
3.1 免疫算法
免疫算法(immune algorithm,IA)是模仿生物免疫机制,结合基因的进化机理,人工构造出的智能优化算法[12]。免疫算法是启发算法的一种,采用群体搜索策略,通过迭代计算得到问题的最优解。免疫算法具备较强的全局收敛性,能够弥补模拟退火算法全局搜索能力差的问题。表1 为免疫系统与免疫算法的对应关系。

表1 免疫系统与免疫算法对应关系Table 1 Correspondence between immune system and immune algorithm
免疫算法的基本步骤如下:
Step 1 分析目标优化问题,构建亲和度函数,设定各类参数;
Step 2 选取预设数量的解生成初始抗体群,问题的可行解即为抗体;
Step 3 计算抗体亲和度;
Step 4 判断算法是否满足终止条件,满足终止条件则输出最优解,否则进入下一步;
Step 5 计算抗体浓度和激励度;
Step 6 免疫选择,然后对抗体进行克隆、变异和克隆抑制;
Step 7 更新抗体群,并返回至Step 3。
免疫算法的构成要素如下:
1)免疫选择:在计算出抗体亲和度后,选择出优质抗体,即相对最优解。
2)克隆:对选择出的优质抗体进行复制,得到多个优质抗体。
3)变异:对克隆出的优质抗体重新编码,改变其亲和度。
4)克隆抑制:对上述优质抗体再次进行筛选,留下高亲和度抗体,剔除低亲和度抗体。
3.2 解的编码方式
WTA 模型中火力单元和目标均需要进行编码,因此,本文采用矩阵编码的方式,假定6 个火力单元打击5 个目标,粒子编码记为xk5×6(i),表示算法第k 次迭代第i 个粒子的武器目标分配方案。如表2 所示,武器2 打击目标2,值为1;值为0 时,表示不打击。
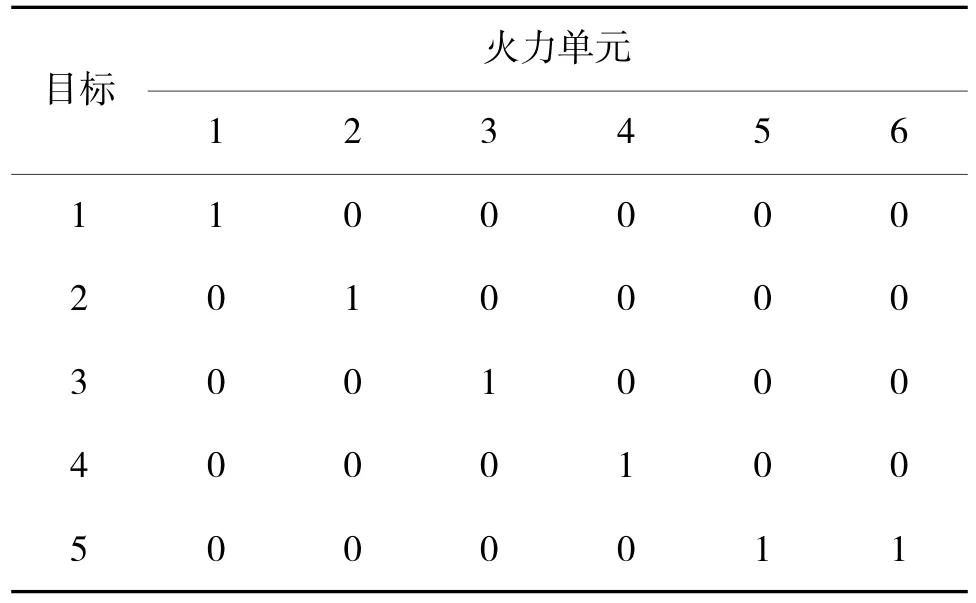
表2 编码方式示例Table 2 Example of encoding method
3.3 改进免疫模拟退火算法
在使用模拟退火算法解决WTA 问题的过程中,出现算法效率较低的情况,因此,本文借鉴文献[13-15]中提出的利用免疫算法与模拟退火算法相结合的方法来改善模拟退火算法效率低下的缺点。传统的免疫算法利用浓度指标选取优质抗体,本文选择亲和度作为主要指标,应用Metropolis 准则更新抗体群,也就是以一定概率接受劣质抗体,具备跳出局部最优的能力。到了搜索后期,温度下降,进而减少了接受劣质解的概率,算法的收敛速度明显增大,算法的全局搜索能力也会增强。
3.3.1 初始抗体群与亲和度
在WTA 问题中,将每一种分配方案也就是解视为一个抗体,将适应度函数视为抗原,那么亲和度就是解对应适应度函数的值。在本文中亲和度越大,适应度函数的值越高,即f 的值越高,代表解越优质,武器目标分配方案越合理。
3.3.2 免疫选择与克隆抑制
传统免疫算法的免疫选择,会在亲和度高、浓度低的抗体中产生新解,但这种操作容易陷入局部最优。本文的改进算法根据模拟退火思想中的转移概率,以一定概率P 接受劣质抗体,进行交叉变异操作来增加种群多样性。概率P 的值如下:
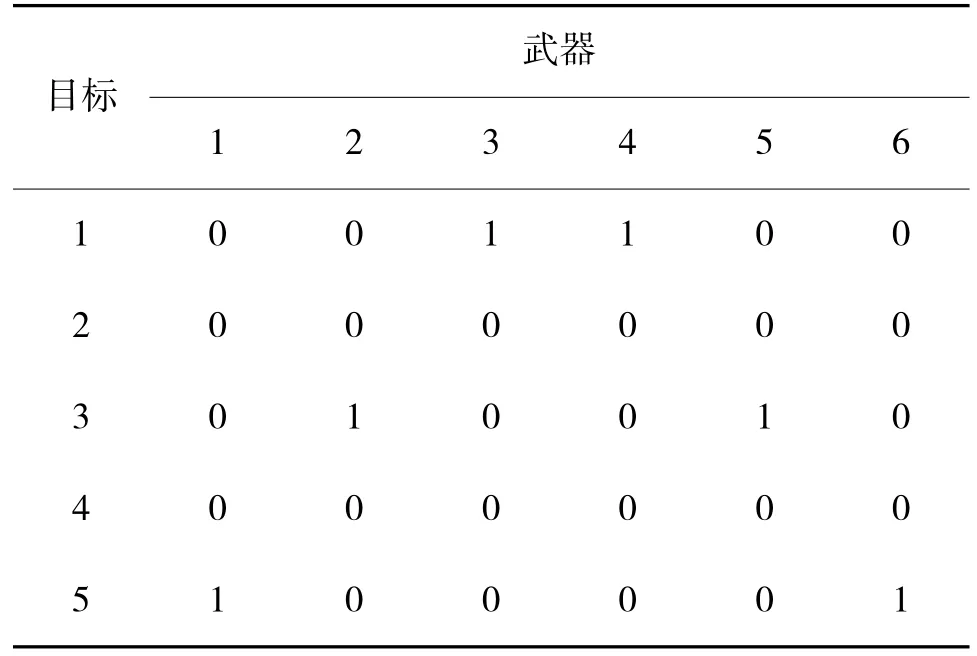
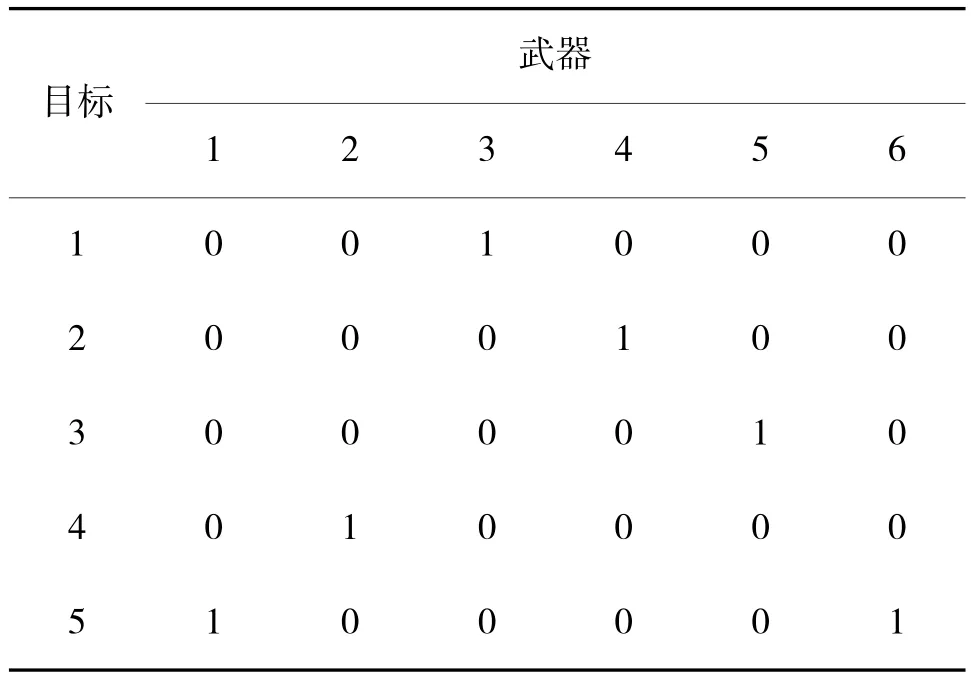
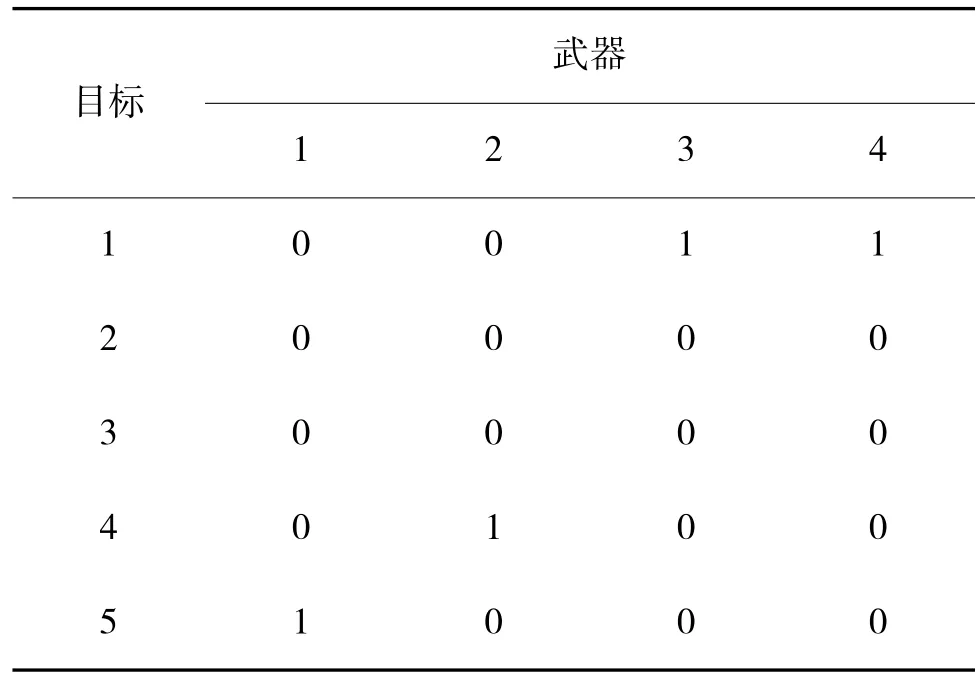
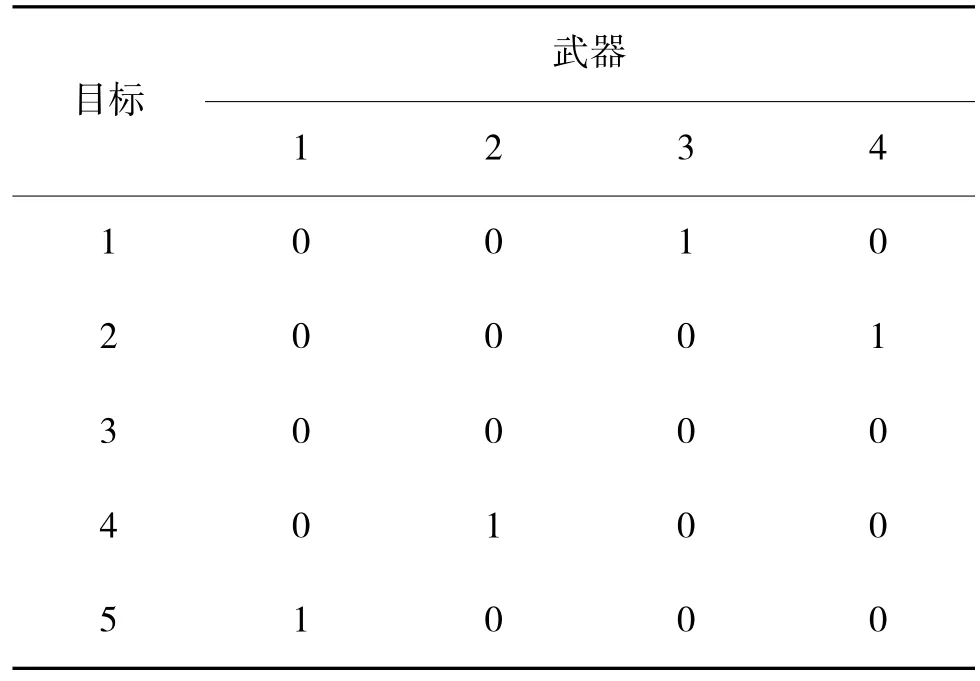
其中,f 表示当前抗体的亲和度;f'表示新生成的抗体的亲和度;f 表示所有抗体平均亲和度。当f '>f时,保留新抗体;当f' 3.3.3 克隆、交叉和变异 对优质抗体进行克隆,克隆数量设定为: 克隆所得到的优质抗体用于交叉和变异操作。交叉一般是将两个可行解中的局部进行互相交换,从而产生新解。在本文中的交叉操作为: 其中,y 表示交叉产生的新抗体;x1表示待交叉抗体;x2表示被克隆的抗体;rand 是[0,1]之间生成的随机数。 变异操作限制如下:针对优质抗体,随机选取编码中两位,并将它们的值交换。交叉变异操作完成后,将产生的新抗体加入的抗体群中形成新的抗体群。 改进后算法的步骤流程图如图1 所示。 图1 算法流程图Fig.1 Algorithm flowchart 假定防空火力单元有6 个,空袭目标有5 个,进行仿真实验。为了便于研究算法和WTA 问题,本文设定6 个防空火力单元同为某型弹炮结合防空武器系统,5 个空袭目标同为某型无人机,火力单元对匀速运动的目标实行一次点射。 为充分验证改进算法求解WTA 问题的有效性,特设计两种作战场景下的对比实验。第1 种场景为火力单元数量(6 个)多于空袭目标数量(5个);第2 种场景为火力单元数量(4 个)少于空袭目标数量(5 个)。在进行第2 种场景下的实验时,只有武器编号为1~4 的火力单元参与作战。 目标的威胁度和各火力单元对目标的毁伤概率如表3 所示。 表3 威胁度及毁伤概率表Table 3 Threat degree and damage probability table 设定实验相关参数,模拟退火的初始温度T0设为100℃,降温函数的冷却参数α 设为0.9,算法终止温度Te设为1℃,迭代次数设为200。算法种群规模设为150,比例因子rand 的范围为[0,1]。分别使用标准模拟退火算法和本文的改进免疫模拟退火算法对WTA 问题进行求解分析。 两种场景下标准算法和改进算法对WTA 模型的求解结果的对比,场景1 的分配结果如表4 和表5 所示;场景2 的分配结果如表6 和表7 所示。 表4 场景1 标准模拟退火算法的解Table 4 Solution to standard simulated annealing algorithm in scene one 表5 场景1 改进免疫模拟退火算法的解Table 5 Solution to improved immune simulated annealing algorithm in scene one 表6 场景2 标准模拟退火算法的解Table 6 Solution to standard simulated annealing algorithm in scene two 表7 场景2 改进免疫模拟退火算法的解Table 7 Solution to improved immune simulated annealing algorithm in scene two 在火力单元数量多于空袭目标数量时,表4 的分配结果中部分目标没有分配到火力单元,而部分目标分配到的火力单元过多;在火力单元数量少于空袭目标数量时,表6 分配结果中的目标1 同时被分配到两个火力单元,而目标2 和目标3 没有分配到火力单元。说明标准算法在求解WTA 问题时,会出现陷入局部最优的情况,体现到求解结果中,就是武器和目标分配不合理,造成火力资源浪费和未打击目标数量超常的情况。 而在表5 和表7 中,改进算法的分配结果相较于标准算法更为科学,保证了更多的目标分配到火力单元,更为有效地利用了火力资源。 其次,在算法方面,场景1 下两种算法的对比如下页图2 所示。 图2 场景1 算法对比图Fig.2 Comparison chart of algorithm in scene one 改进免疫模拟退火算法在迭代了60 次左右就开始收敛,而标准算法在迭代到接近120 次才开始收敛,改进算法的收敛速度明显要比标准算法快很多。改进算法最终的适应度值为2.64,标准算法的适应度值最终为2.11,改进算法的全局最优解的质量要更高。 在对场景2 的实验重复进行100 次后,两种算法的对比效果如表8 所示。 表8 算法对比效果图Table 8 Comparison effect chart of algorithm 改进免疫模拟退火算法的平均最优适应度值要高于标准算法,100 次实验中能够达到最优解的实验次数也更多。在算法迭代速度方面,改进算法同样优于标准算法,改进算法的平均迭代时间要比标准算法短0.53 s。 针对模拟退火算法在求解WTA 问题时搜索效率低,求解全局最优能力差的问题,本文提出一种结合免疫算法和模拟退火算法的改进算法,选择亲和度作为适应度指标,利用Metropoli 准则避免局部最优,利用模拟退火中降温操作加快搜索,改善算法收敛能力。设计仿真实验对改进算法的有效性进行验证,并求解WTA 问题。对算法迭代次数的设置和降温函数的优化,未来还需要进一步的研究。3.4 改进免疫模拟退火算法的步骤

4 实验验证与结果分析
4.1 仿真实验
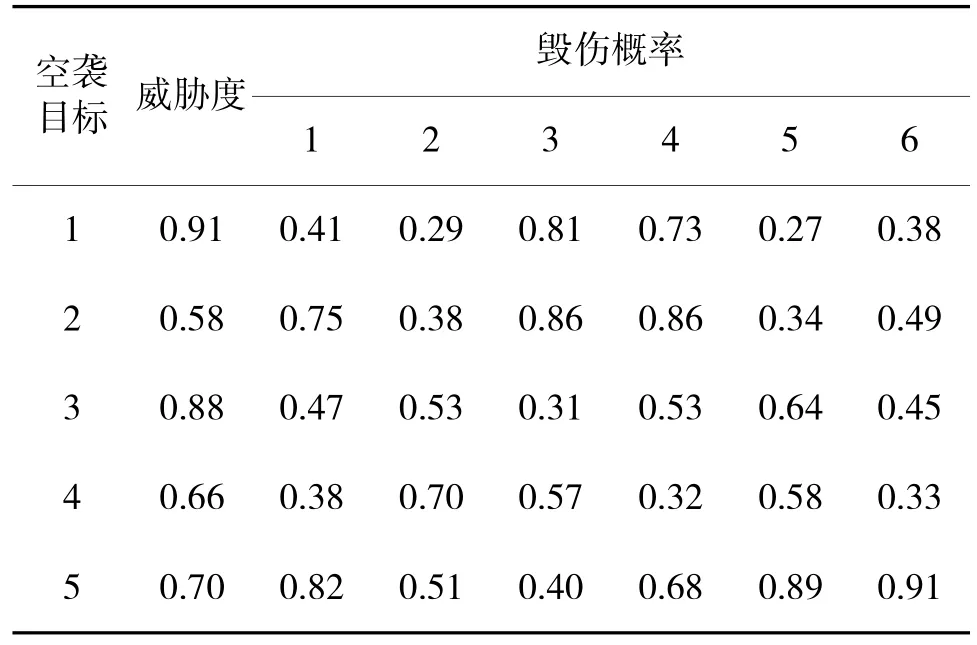
4.2 结果分析


5 结论

