基于粒子群算法的空战决策问题研究*

徐振森，王建军，赵燊佳，张 军*，王玺琛

（1.南京航空航天大学航空学院，南京 210016；2.中国运载火箭技术研究院，北京 100076）

0 引言

协同作战以低成本、可替代的特点成为国际研究的热点［1-2］。而空战决策问题在协同多目标攻击、超视距空战中具有重要作用，现已证明其是NP 问题［3］，但仍然没有非常完美的算法解决此问题［4］。刘杰等研究了基于黑板模型的分布式协同任务决策方法，运用遗传算法，针对航母攻击多目标的作战想定，建立数学模型，得出了基于负载的衡量标准，给这一类问题提供了有效参考［5］；WEN 等选取速度、距离等要素构建态势评估函数，采用粒子群算法（particle swarm optimization，PSO）进行仿真验证，证明了该空战决策模型的可行性［6］。国内外专家学者也通过改进惯性权重、加速因子取值方法改进粒子群算法寻优问题，CLERC 等基于模糊技术，提出一种新的惯性权重模糊自适应模型和相应的粒子群优化算法，加快了粒子群的收敛速度［7］；PATNAWEERA 等结合遗传算法思想，直接对粒子进行交叉、变异操作更新粒子，提高了求解空战决策问题的有效性［8］。

针对离散型规划问题的二进制粒子群优化算法（binary particle swarm optimization，BPSO）的求解思路是粒子所代表的解在离散空间内以矢量运算的形式进行更新迭代，并进行随机或局部搜索［6］。而该算法的实现局限于速度——位置更新算子，针对BPSO 算法易过早收敛、陷入局部最优解以及种群多样性小的问题，本文探索、对比、分析结合遗传算法、免疫算法、模拟退火算法改进的PSO 算法，优化速度——位置更新算子，求解静态空战决策模型，找出最佳求解算法，以期提升空战决策问题的解决方案质量。

1 空战决策问题简化模型

1.1 空战决策问题描述

在真实空战决策过程中，目标和我方作战平台及武器装备并非简单的一一对应关系，武器精准度、交战位置、距离、目标攻击能力等因素都会影响最终作战效果。本文简化决策问题，考虑敌方武器装备对我方作战平台的综合威胁，以及我方武器装备毁伤目标的概率，预设想定情景，进行模拟仿真［9］。

设我方编队有M 架飞机，编队共携带R 枚导弹，敌方为N 个目标。设Pkj为第k 枚导弹毁伤第j个目标成功率。当第k 枚导弹分配给第j 个目标后，目标的生存概率为1-Pkj。令Xkj为导弹k 对目标j的决策结果，0 是不分配，1 是分配。所有M 架飞机协同攻击后，目标j 的生存概率为：

设我方飞机数目为4，每机携带2 枚导弹，目标数量为6，随机抽取（0，1）内的随机数形成8×6 列表，表征8 枚导弹对6 个目标的命中率，命中率想定表如表1 所示。

表1 导弹命中率想定表Table 1 Scenario table of missile hit rates

随机抽取（0，1）内的随机数形成4×6 列表，表征6 个目标对我方4 架飞机的威胁值想定，如表2 所示。

表2 目标威胁值想定表Table 2 Scenario table of target threat values

1.2 目标函数

空战目标威胁值根据敌我双方的武器性能以及时空指标评估计算得出［10］。威胁排序是根据威胁评估值、我方武力评估值以及战术目的优先级综合得出的作战顺序，是目标分配的依据。

假设目标j 对我机i 的威胁值为Tij，则可建立第一个目标函数：

其中，Pj为目标j 被攻击后的生存概率；M 为我方飞机数量；N 为目标数量。式（2）表示作战后，剩余目标威胁评估函数最小期望值。我方对敌作战最大毁伤概率期望值为第2 个目标函数：

空战决策问题是一个多目标函数的问题，对其进行简化后利用粒子群算法进行求解。本文中使用线性加权和法对两个目标函数进行简化，根据两个目标函数的重要程度设置权重系数，设目标函数（2）的权重系数为ω1，目标函数（3）的权重系数为ω2。则目标函数可化为：

空战决策首要目的在于摧毁敌方力量，削弱敌方对我方的威胁，因此，初始化设置权重系数ω1=0.6，ω2=0.4。

1.3 约束条件与罚函数实现

在仿真模拟中，一枚导弹只能分配一次，并尽可能多地取得战果，约束条件可表述为：

式中，Xkj∈{0，1}为第k 枚导弹分配给第j 个目标的决策结果，0 为不分配，1 为分配。第1 约束条件为编队导弹进攻总数不大于R 枚，第2 约束条件为1枚导弹不能分配多次，第3 约束条件为针对每个目标进行导弹分配。

式（5）中约束条件多，若全部用罚函数实现，将严重影响搜索的效率，因此，本文进行初始化操作，使得初始解满足约束条件。在目标函数中采用罚函数法评估方案优劣，修改目标函数为：

如果违反约束条件，则使NF 取一个较大值，使其偏离收敛值；如果满足约束条件，则使NF 取0，获得符合条件的适应值。在迭代中，粒子的速度分量表征导弹的分配结果。

2 面向多目标空战决策问题的BPSO算法实现

粒子群算法模仿鸟群觅食，设有N 个粒子组成一个群体，每个粒子按照一定规则改变运动方向和距离，并以动态更新的个体极值Pbest和群体极值Gbest调整飞行状态，更新速度vi（t）和位置xi（t），趋向最优解［11］。飞行状态更新公式：

式中，vi（t）为粒子的速度；xi（t）为粒子当前的位置；ω为惯性权重因子；c1、c2调节粒子倾向于Pbest和Gbest的步长；r1和r2为（0，1）之间的随机数，t 为迭代代数。

利用BPSO 算法实现协同多目标空战决策的算法流程图如图1 所示。

图1 BPSO 算法流程图Fig.1 Flow chart of BPSO algorithm

已知最优全局极值为1.107 724，最优全局极值点（最优解）为：

3 改进的粒子群算法

BPSO 算法易过早收敛、陷入局部最优解且种群多样性小，解决这些问题的关键点在于扩大粒子群多样性［12］。本文结合遗传算法、免疫算法、模拟退火算法思想改进BPSO 算法，优化速度——位置更新算子，形成结合遗传算法的离散粒子群检测算法（discrete particle swarm detection algorithm，DPSODA）［13-15］、基于免疫记忆和调节机制的免疫记忆粒子群优化算法（immune memory particle swarm optimization algorithm，IM-PSO）［16］以及模拟退火融合粒子群算法（simulated annealing fusion particle swarm optimization algorithm，SA-PSO）［17］，改善迭代过程中粒子群的多样性，避免过早陷入局部最优解。

3.1 DPSO-DA 算法

郭文忠等设计了一种离散PSO 算法（DPSO-DA）［15］，DPSO-DA 算法相比BPSO 算法，引入了个体相似性、个体多样性、群体多样性、变异算子等定义：

定义1 个体相似性。个体相似性Sij刻画了个体i 和个体j 值之间相似程度：

其中，k 表示第k 个基因位，即粒子的第k 维分量，m表示粒子位置向量的维数。

定义2 个体多样性。个体多样性Ci（t）表示粒子X（i）与其个体极值及全局极值三者之间的相似度：

其中，Pfbest、Gfbest分别表示粒子i 的个体极值和种群的全局极值；Si，Pfbest（t）表示粒子i 当前位置与其个体极值的个体相似性；Si，Gfbest（t）表示粒子i 当前位置与全局极值的个体相似性；SPfbest，Gfbest（t）表示粒子i 的个体极值和种群全局极值的个体相似性。

定义3 群体多样性。群体多样性D（t）是在描述群体任意两粒子之间的相似程度：

其中，D（t）=0 表示所有粒子两两相同，反之，D（t）=1则表示所有粒子间两两完全不同。

定义4 变异算子⊕。设X（i）为粒子的当前位置，根据粒子i 的个体极值Pxbest（i），按照变异规则进行变异算子的操作，即Pv=Pxbest（i）⊕X（i）。通过变异算子来改变粒子的更新速度V（i），从而增加个体多样性或群体多样性。其中，pv 的每一维分量由以下公式确定：

其中，pvd是粒子i 更新的速度d 维分量；Xid是粒子i 当前位置d 维分量；pxbestid是粒子i 个体极值d 维分量。

每代更新粒子状态都需要计算各粒子的个体相似性，进而求得个体多样性、群体多样性，当二者低于阈值c、d 后，对每个粒子进行变异算子操作。DPSO-DA 算法流程图如图2 所示。

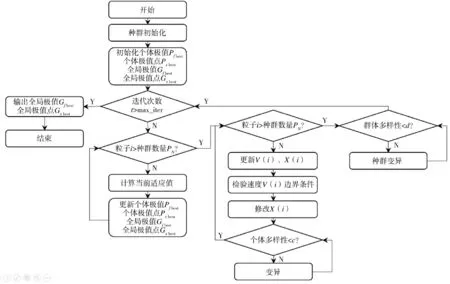
图2 DPSO-DA 算法流程图Fig.2 Flow chart of DPSO-DA algorithm

3.2 IM-PSO 算法

抗体多样性和免疫记忆是生物免疫系统的重要特征，生物免疫系统产生的抗体和外来入侵抗原相结合，与抗原进行反应，从而消灭抗原。基于免疫记忆和调节机制的改进粒子群优化算法叫作免疫记忆粒子群优化算法（immune memory particle swarm optimization algorithm，IM-PSO）［16］，IM-PSO 算法引入了粒子浓度、记忆细胞选择概率，以保证在迭代过程中保留多样的样本种群。

定义5 粒子浓度。在更新过程中，BPSO 会逐渐淘汰适应度低的粒子，包括一些适应度较差却保持着良好趋势的粒子，导致目前适应度好的粒子（抗体）过于集中（浓度太高），陷入局部最优解。因此，本文使粒子群中各层次粒子都有一定浓度。第i个粒子的浓度D（Xi）定义：

其中，M 表示种群数量，f（Xi）为第i 个粒子的适应值。

定义6 记忆细胞选择概率。为使种群中留下各个层次的粒子（抗体）作为记忆细胞进行下一步操作，本文定义基于粒子浓度的概率选择P（Xi）公式：

每代迭代过程中，随机添加若干粒子，计算所有粒子的浓度，根据浓度求出记忆细胞选择概率，并依照概率排序选择出pN 个粒子，建立新的种群。IM-PSO 算法流程图如图3 所示。

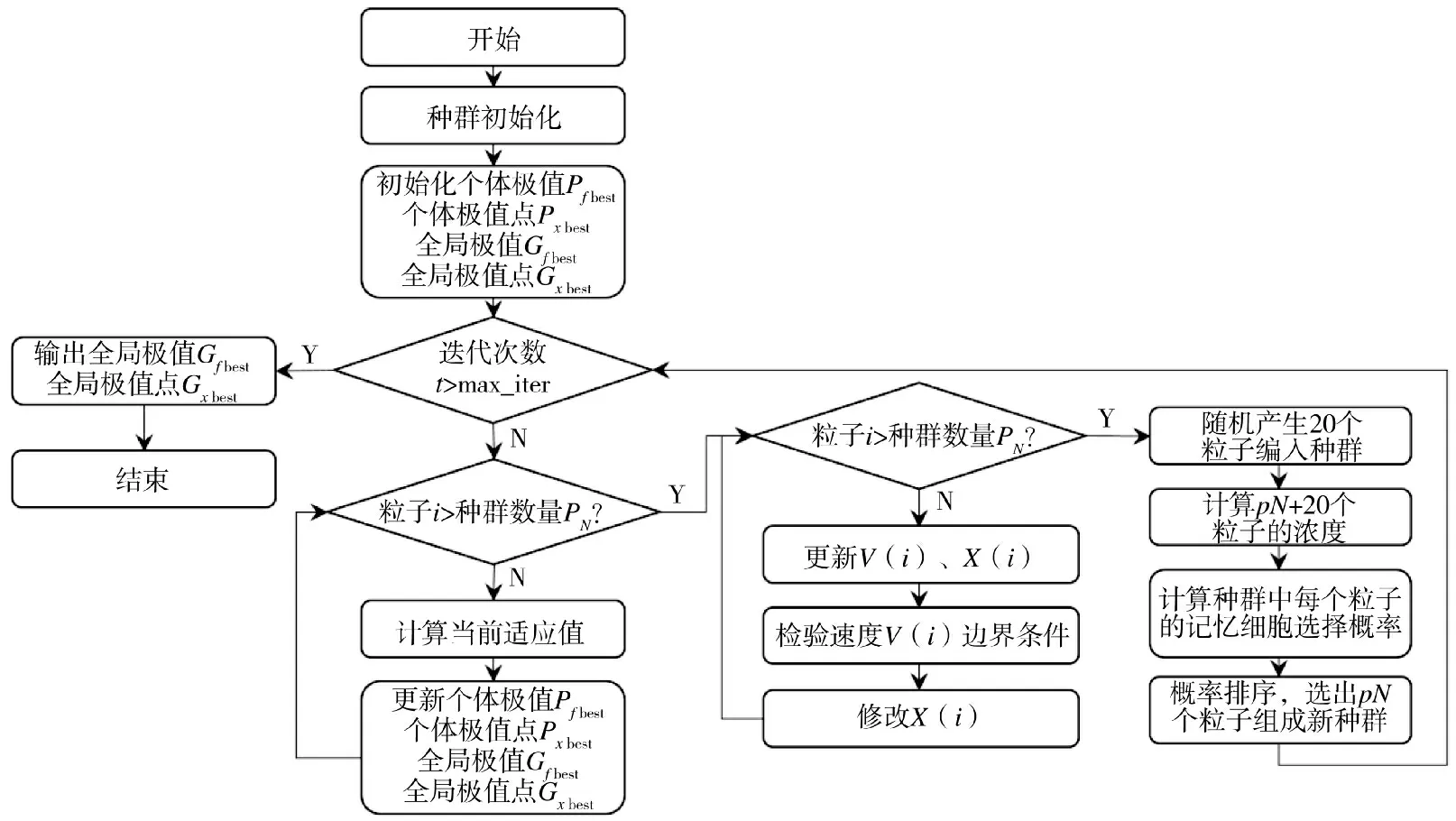
图3 IM-PSO 算法流程图Fig.3 Flow chart of IM-PSO algorithm

3.3 SA-PSO 算法

模拟退火算法（simulated annealing，SA）［18］是在模仿燃烧固体降温的过程，在迭代过程中对当前解Xold进行随机概率扰动，以产生新解Xnew。若新解适应度较好，则接受它作为当前解；若新解适应度较差，则以一定的概率接受为当前解，直到温度降低到指定位置。这种算法以一定概率接受适应度较差的解，因此，不易陷入局部最优解而过早收敛。

为了将模拟退火算法引入BPSO 算法，采用交叉变异等操作［17］。在每次迭代中，随机筛选出要进行交叉的一对父代粒子，父代粒子杂交出子代粒子。父代粒子速度向量按以下公式杂交出子代粒子速度向量：

其中，Δf 为当前解xold和xnew适应值的差值，Tk为第k 次迭代的退火温度，用式（18）更新：

其中，C∈（0，1）为温度冷却系数。

当Pc＞E 时，接受子代粒子作为迭代结果，并进行下一代迭代。SA-PSO 算法流程图如下页图4所示。

图4 SA-PSO 算法流程图Fig.4 Flow chart of SA-PSO algorithm

4 仿真研究

本文以静态多目标空战决策问题为研究对象，建立数学模型，并根据目标的威胁评估和战后目标的生存概率建立目标函数；运用线性权重法，把多目标简化为单目标函数；根据约束条件，用罚函数思想修正目标函数。在随机生成初始解的过程中，使其符合约束条件，并且在迭代中对解进行约束，减少无效迭代，并利用BPSO 算法进行50 次求解计算。同样条件下，使用DPSO-DA、IM-PSO、SA-PSO 算法对空战决策问题进行求解，得到仿真结果特征如表3 所示。

表3 BPSO 及改进算法计算结果特征表Table 3 Characteristics table of calculation results of BPSO and improved algorithm

以各算法的成功率、平均收敛值、错误解数量、最差解、方差数据绘制雷达图如图5 所示。

图5 4 种算法结果对比图Fig.5 Comparison result diagram of four kinds of algorithms

BPSO 算法成功率较低为18%，表现一般但却较稳定；DPSO-DA 算法相比BPSO 算法，成功率从18%提高到了44%，成功率最高平均收敛值从1.187 73优化至1.156 94，方差大幅降低；IM-PSO 算法成功率为26%，平均收敛值为1.165 92，方差为0.007，稍逊于DPSO-DA 算法，但仍较BPSO 算法优异；SAPSO 算法成功率为8%，平均收敛值为1.315 92，大部分为不合格解，表现差于BPSO 算法。

取4 次迭代历史适应值曲线绘制对比图，如下页图6 所示。

图6 4 种算法迭代历史适应值曲线对比图Fig.6 Comparison curve of iterative history adaptation values of four kinds of algorithms

由图6 可知，SA-PSO 算法最不稳定，收敛速度最快且最容易得到错误解；DPSO-DA 算法和IM-PSO 算法较BPSO 算法收敛速度较慢，改进效果显著，其中IM-PSO 算法收敛速度最理想。结合结果特征数据可知，DPSO-DA 算法改进效果相对最佳。

5 结论

本文针对BPSO 算法在静态空战决策问题求解过程中出现的过早收敛、易于陷于局部最优解的问题，结合遗传算法、免疫算法、模拟退火算法尝试优化BPSO 算法，改进速度——位置更新算子，达到了扩大种群多样性、改善陷于局部最优解困境的目的。其中，DPSO-DA 算法以及IM-PSO 算法改善效果较为明显，但SA-PSO 算法反而有所下降，其中原理有待于进一步研究。