长宽比对双进水管结构矩形圆弧角养殖池排污特性的影响

史宪莹，李猛，2，任效忠，冯德军，刘航飞，周寅鑫，刘海波，2，赵晨旭，2

(1.大连海洋大学 海洋与土木工程学院，辽宁 大连 116023；2.设施渔业教育部重点实验室(大连海洋大学)，辽宁 大连 116023；3.大连海洋大学 海洋科技与环境学院，辽宁 大连 116023；4.浙江海洋大学 国家海洋设施养殖工程技术研究中心，浙江 舟山 316022；5.浙江大学 生物系统工程与食品科学学院，浙江 杭州 310058)

中国是世界水产养殖第一大国，水产养殖产业在保障蛋白供给、稳定水产品市场和促进贸易发展等方面都发挥了重大作用，成为战略性的新兴产业之一[1-2]。循环水养殖具有生产效率高、占地面积少、可控性强和水产品质量安全等优点，被认为是21世纪水产养殖业发展的主导方向[3]。在循环水养殖过程中，养殖池内容易堆积由粪便、残饵和鱼体黏液等组成的固体废物[4-5]。固体废物的累计和分解矿化会对鱼类健康及养殖池水质产生负面影响，甚至还会导致循环水设施的堵塞，影响设备的正常运行[6-7]。因此，高效、快速地清除养殖池内的固体废物，对保证鱼类健康生长，避免池内水质下降，维持循环水设备的正常运行具有重要意义。

目前，构建高效的循环水养殖系统已成为水产养殖行业研究发展的方向，而管理和去除养殖水体中的悬浮颗粒物又是循环水养殖系统的关键环节[8]。在循环水养殖系统中，养殖池的池形及相关参数的优化对池内的排污效果具有直接影响。对圆形养殖池排污效果的研究表明，养殖池进出水结构、进水流量和水的循环周期等参数的变化对养殖池的固体冲刷效果均有较大影响[9-12]。Liu等[13]应用DPM模型模拟八角形养殖池的排污性能，并进行了物理试验验证，结果表明，该模型能较为准确地模拟八角形养殖池内固体颗粒的运动轨迹。Gorle等[14]对八角形养殖池进、出水口的位置研究表明，进、出水口位置参数的变化对养殖池内速度、涡量和湍流等水力特性均有影响，养殖池设置底部排水口和转角进水口可以增强水流旋转流动，使水体拥有更好的均匀性，从而确保了养殖池自清洁能力的提高。在对养殖池的相关研究中，桂劲松等[15]对矩形养殖池进行了圆弧角优化，优化后的矩形圆弧角养殖池兼具较好的流场性能和较高的空间利用率。对矩形圆弧角养殖池内的排污性能研究表明，养殖池内水体的日循环次数、进水孔入射角度、径深比和排污粒子的特性等相关参数设置对养殖池内固体颗粒物的清除均有较大影响[16-19]。在已有关于矩形圆弧角养殖池的排污优化研究中，养殖池的规格多为单一固定的，较少有学者进行养殖池长宽比变化的排污数值模拟研究。在矩形圆弧角养殖池实际建设过程中，通过改变养殖池的长宽比进行适当的池形变化，可适应不同场地建设要求，但随着长宽比的增加，矩形圆弧角养殖池内流场的环流状态发生改变，可导致池内排污效果发生改变[20]。因此，探究具有较好排污性能的长宽比参数区间，是养殖池优化研究中亟待解决的问题。

本研究中，通过数值模拟研究不同长宽比参数条件下矩形圆弧角养殖池的排污特性，通过构建固-液两相流数值模型，定义了适用于较大长宽比池形的重叠撒布方式，对两种进水管布置位置的不同长宽比工况进行排污模拟试验，得到具有较好排污性能的最优长宽比参数区间，以期为矩形圆弧角养殖池实际建设中池形尺寸的选择提供参考和借鉴。

1 材料与方法

1.1 养殖池数值模型构建

根据实际养殖池规格以1∶8比例缩小构建矩形圆弧角养殖池数值模型。将养殖池长宽比设置为可变参数，建立10个不同长宽比的计算工况，每个工况长宽比间隔为0.1。养殖池长(L)×宽(B)为(1.0～1.9 )m×1.0 m，以方形圆弧角养殖池(L/W=1.0)为例，模型结构如图1所示，在养殖池边壁中心对称布置双进水管，每个进水管设置9个直径为0.004 m的射流孔，射流孔与池边壁夹角为0°。养殖池采用中心底部单排水管结构排水，排水管直径为0.02 m，水深H=0.2 m(即径深比B/H=5∶1)，相对弧宽比R/B=0.25(R为圆弧角半径)，进径比C/B=0.03[21](C为射流孔位置到养殖池壁的水平距离)。为保证不同长宽比的养殖池内水体循环次数保持100次/d，射流孔面积与长宽比保持成比例变化，长宽比参数变化为1.0～1.9，采用的入流流量为814～1546 L/h，进水口射流速度恒为1 m/s。养殖池参数见图1。

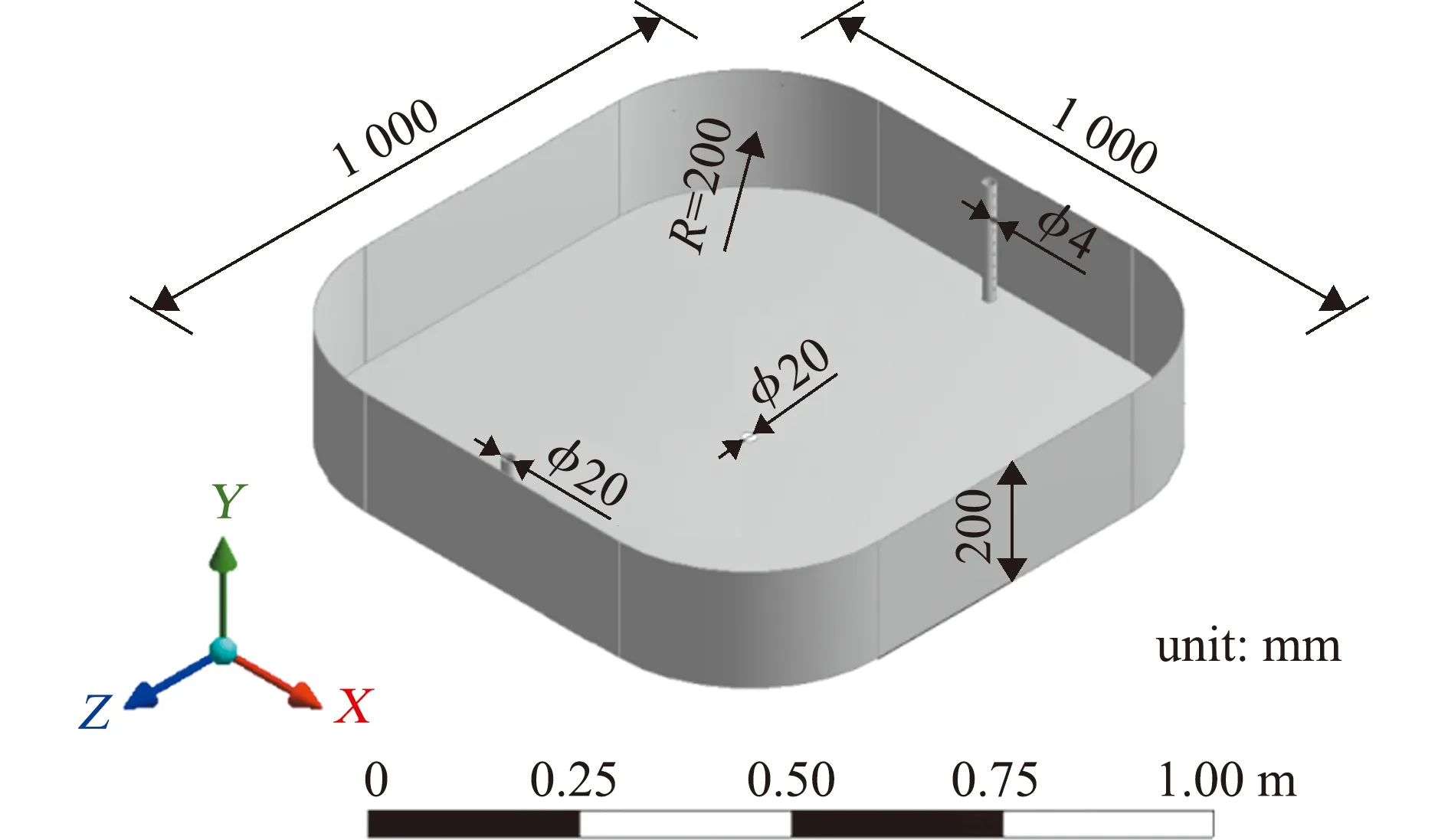
图1 养殖池参数Fig.1 Parameters of culture tank

随着长宽比的变化，养殖池形状从方形圆弧角向矩形圆弧角转变，这带来两种不同的进水管布设方式，即进水管布置在长边中心位置和宽边中心位置(图2)。

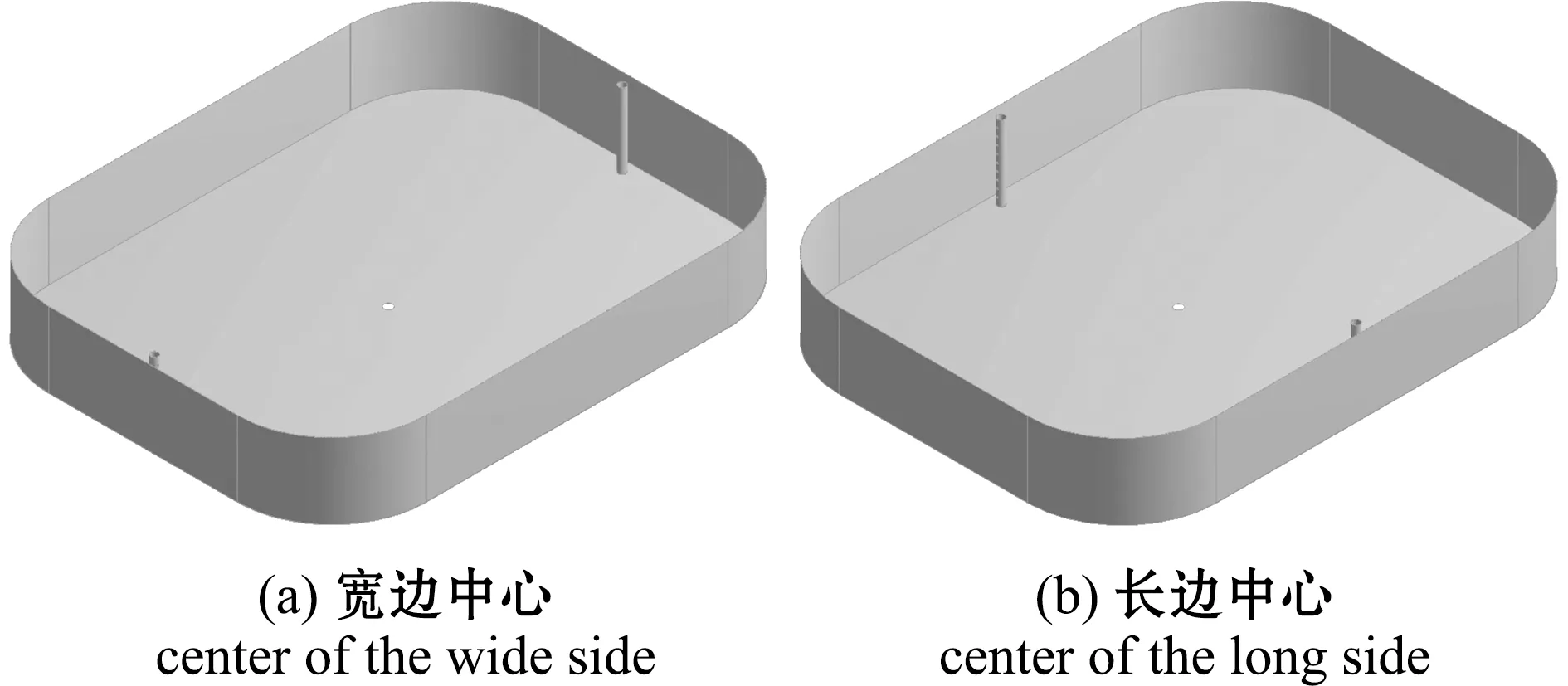
图2 养殖池两种布管方式Fig.2 Two kinds of fabric and tube in culture tank

1.2 控制方程

1.2.1 湍流模型 Yakhot等[22]应用重整化群(Renormalization Group，RNG)理论，建立了一类新的湍流模型——RNGk-ε湍流模型。即将重整化群方法用于N-S方程，并引入湍能k及耗散率ε，相较于标准k-ε模型，RNGk-ε湍流模型提供了低雷诺数流动黏性的解析公式，使其更好地模拟近壁区域的流动。RNGk-ε湍流模型能更好地处理高应变率、流线弯曲程度较大的流动，以及湍流中的涡效应。RNGk-ε其连续性方程为

(1)

RNGk-ε动量方程为

(2)

式中：ρ和μ分别为液体的密度(kg/m3)和黏度(Pa·s)；t为经过时间(s)；u、v、w分别为沿x、y、z轴的速度分量；p为压力(N)；i=1，2，3分别对应x、y、z3个方向的变量；Sui为动量方程的源项，Sui=Fxi+Sxi，对于不可压缩流体Sxi=0，Fxi为引力(N)，因此，Su=Fx=0，Sy=Fy=0，Sw=Fz=-ρg。

RNGk-ε输运方程[23]为

(3)

(4)

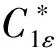
μeff=μ+μt，

(5)

(6)

η=(2Eij·Eij)1/2k/ε,

(7)

(8)

式中：μt为湍流黏度(Pa·s)；C1ε=1.42，η0=4.377，β=0.012；η为湍流流场的速度张量；Eij为时均应变率。

1.2.2 离散项模型 养殖池系统构建的固-液两相流模型，在模拟两相耦合过程时，首先计算得到收敛的连续相流场，然后在连续相内创建离散相粒子进行耦合计算。每一轮离散相的计算要考虑养殖池内水体与固体颗粒之间动量、速度和位置的交换。由于本试验设置投放的固体颗粒物体积分数占比远小于水的体积(低于0.1%)，离散项对连续相的影响也远小于连续相对离散项的作用，且矩形圆弧角养殖池内流场呈现类似环流的状态，离散相粒子按照一定的轨迹运动，故本试验中假设忽略颗粒间的相互作用和颗粒对连续相的影响。在拉格朗日公式中，利用质点在外力作用下的运动微分方程积分来追踪质点的轨迹。在给定力作用下的平衡方程为

(9)

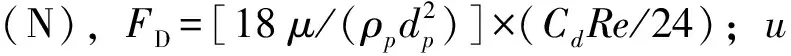
1.3 数值求解方法

本研究中基于固-液两相流模型对三维数值模型进行求解，利用FLUENT 16.0软件中的有限体积法对模型进行了划分，并对控制方程进行离散。连续相和离散相均采用压力隐式求解方法，选用SIMPLE算法对压力速度进行耦合，压力、动量基于二阶迎风离散格式(second order upwind)求解，湍流动能、湍动能耗散率基于一阶迎风离散格式(first order upwind)求解。当所有变量的残差小于0.001时，认为达到了模拟的收敛性。

矩形圆弧角养殖池数值连续相模型和离散相颗粒的进出口边界、交界面处理和壁面边界等初始边界条件如表1所示。

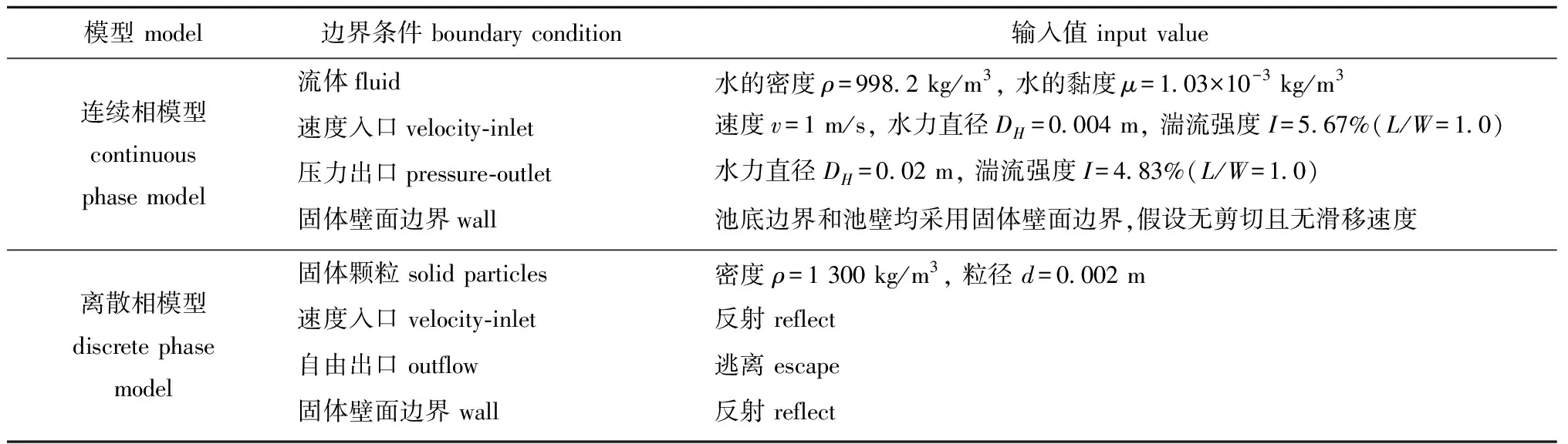
表1 连续相模型和离散相颗粒初始边界条件Tab.1 Initial boundary conditions of continuous phase model and discrete phase particles

1.4 网格划分及网格无关性验证

高质量的网格可以避免模拟试验的数值发散，减小离散误差，简化线性方程求解难度，节省计算时间[24-25]。本研究中，采用混合网格划分技术，以L/W=1.0工况为例，如图3所示，对养殖池主体采用六面体网格划分技术，对进水管、射流孔采用四面体网格进行加密处理，保证在合理的网格数量下，采用高质量的网格单元模拟养殖池较为复杂的区域。网格数量最终控制在60万个左右，最小网格单元尺寸为 0.2 mm，最大网格单元尺寸为 41.65 mm。网格单元的偏斜度(skewness)平均值为0.057，网格质量(element quality)平均值为0.928，纵横比(aspect ratio)平均值为1.4，该网格划分方法保证了良好的网格质量。

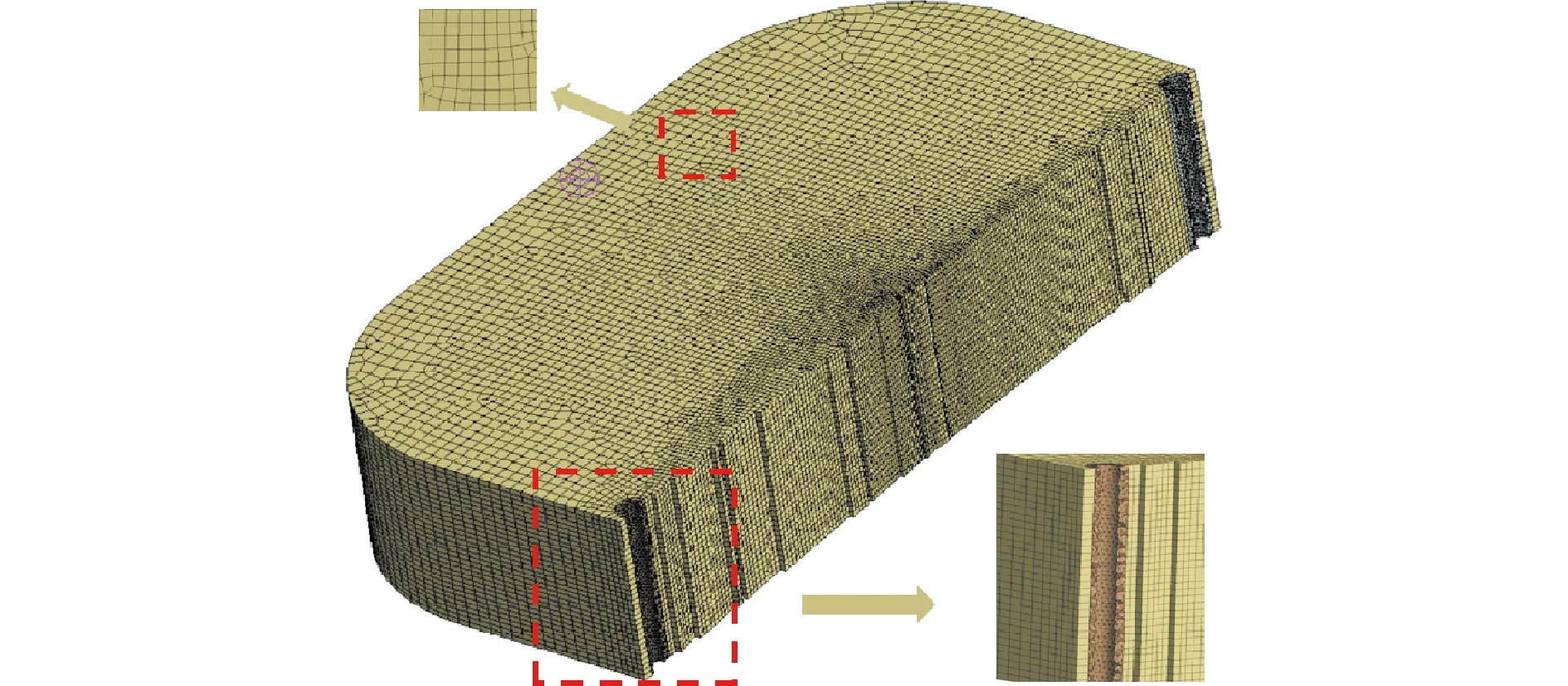
图3 养殖池网格划分Fig.3 Grid division of culture tank

在保证网格质量的同时，合适的网格数量会减少计算时间，提高计算效率。比较网格划分数量分别为40万、50万、60万、90万、120万、150万个的6组工况，选取距池底0.1 m平面的两进水管连接线上16个控制点的数值计算结果进行分析(图4)。

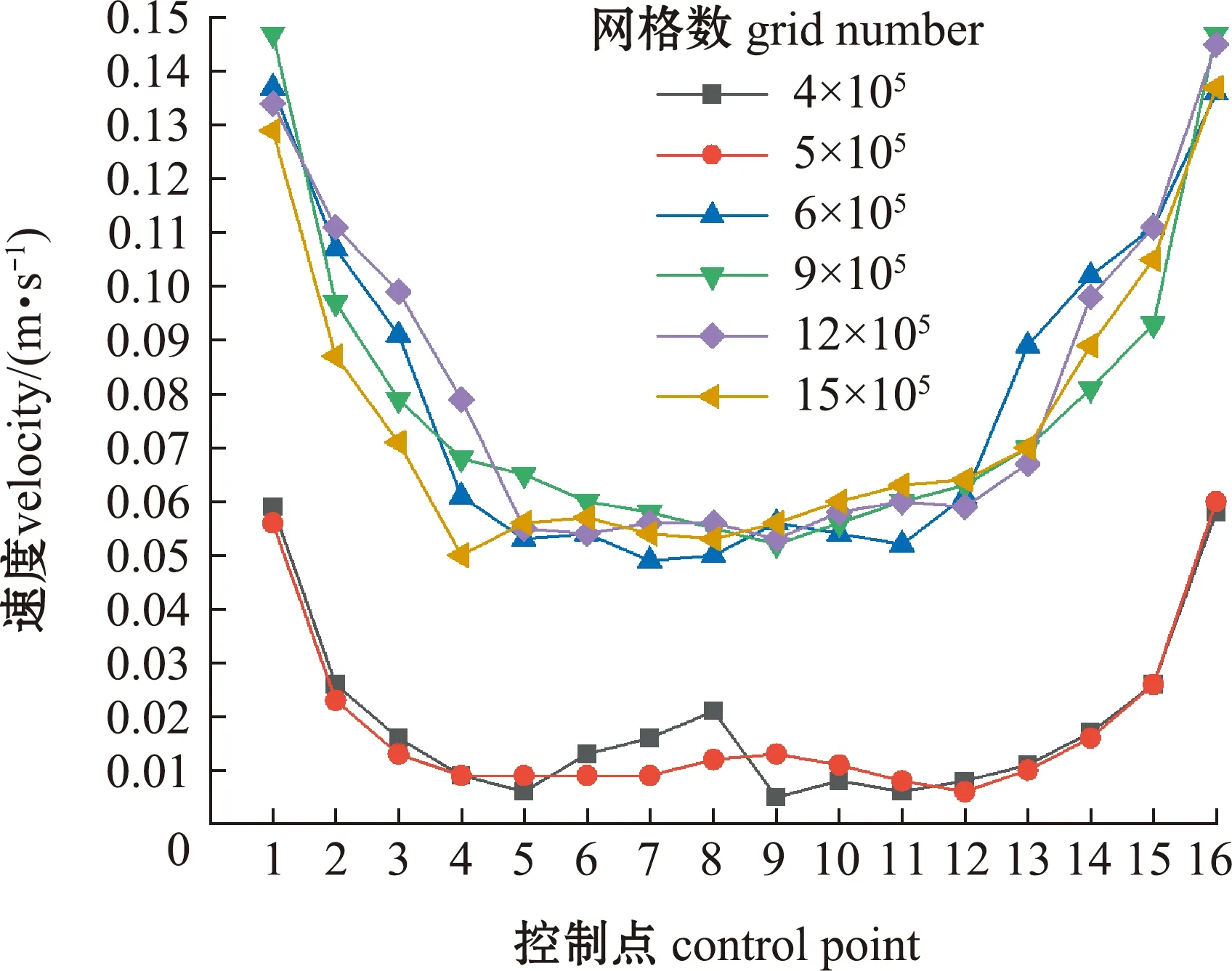
图4 网格无关性验证Fig.4 Grid independence verification

从图4可见：40万、50万个网格工况时，每个控制点的速度明显低于其他工况，说明该网格数量的单个网格单元尺寸较大，对整个养殖池的模拟不够准确；而60万个网格工况与90万、120万、150万个网格工况的各个控制点速度变化趋势相似，大多数对应控制点误差值在10%范围，符合计算精度要求，因此，采用约60万数量的网格进行模拟计算是合理的。

1.5 模型验证

为验证数值计算的合理性，参照任效忠等[17]开展的方形圆弧角养殖池排污特性试验，试验设备见图5(a)。试验步骤：运行试验设备使养殖池内的流场达到稳定状态，向池内均匀撒入20 g沉性饲料(颗粒直径为2.0 mm，密度为1 300 kg/m3，形状系数φ=0.85，数量约为900个)，每隔15 s用拍摄设备俯拍一张池内粒子分布图片，成像效果见图5(b)，试验总时长为3 min。采用Matlab软件对图片进行后处理，计算出各时刻固体颗粒物累计排除率，并对每一工况进行3次重复试验，取其平均值作为试验最终结果。

图5 物理排污试验系统及15 s时池内的粒子分布Fig.5 Physical sewage discharging test system and distribution of particles in the tank at 15 s

数值模拟试验采用与物理试验相同的L/W=1.0试验工况条件，模拟3种不同粒子撒布方式(中心撒布、均匀撒布和重叠撒布)的排污效果(图6)。在DPM模型设置中，规定了粒子撒布的位置和撒布半径，如图6(b)所示，这种中心撒布方式无法模拟较大长宽比池形边角区域的排污状态。针对这一问题，本研究中提出了两种新的粒子撒布方式：均匀撒布和重叠撒布(图6(c)和图6(d))。以L/W=1.5工况为例，均匀撒布方式是将粒子撒布区域分为6个圆形区域，6个区域两两相切，互不重叠，并均匀覆盖整个养殖池；重叠撒布方式是将粒子撒布区域分为4个圆形区域，粒子撒布区域有重叠，重叠撒布位置分布在宽边的中轴线上。这两种撒布方式比中心撒布方式扩大了粒子的撒布面积，更贴近实际养殖池中的排污情况；均匀撒布方式的粒子分布面积低于重叠撒布方式，粒子空间分布率较低，而重叠撒布方式的粒子分布均匀性最好。

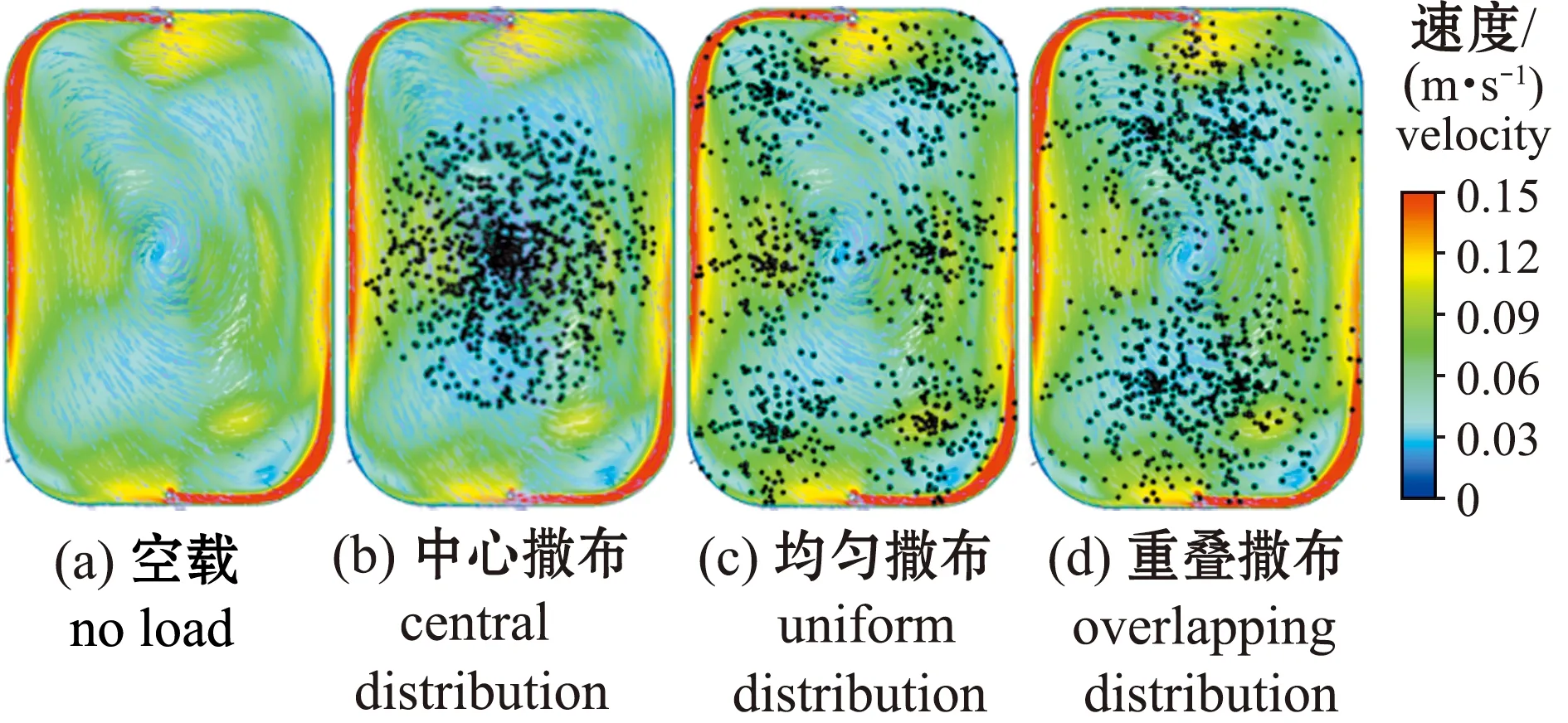
图6 进水管布置在宽边时不同粒子撒布方式Fig.6 Different particle distribution of inlet pipe at the wide edges

当DPM数值模型中的池内流场达到稳定状态后，投入与物理试验相同物理参数的粒子，通过监测池内剩余颗粒的数量计算颗粒物累计排除率，并将3种撒布方式的数值模拟结果与物理试验进行对比，结果表明，数值试验与物理试验结果粒子整体排除率变化趋势吻合较好(图7)。由于物理试验中人工撒布粒子分布率低于数值模拟中的均匀撒布和重叠撒布，而粒子从边角汇聚到中心位置需要一定的时间过程，所以数值模拟试验前60 s的排污效率低于物理试验，在60 s以后，两种方法的试验结果数值相差较小且各时间点对应的粒子排除率趋势一致；但由于物理试验中粒子间的物理参数差异性，导致物理结果总体上略小于数值计算结果，两种方法的粒子最终排除率差值不超过3%。这表明，本研究中建立的数学模型计算精度满足要求，可用于养殖池排污特性研究。

2 结果与分析

2.1 不同粒子撒布方式的排污效果

本研究中，模拟了3组不同长宽比池形内3种撒布方式的排污效果，对比结果如图8所示，在L/W=1.3、1.5的养殖池内，3种撒布方式工况在120 s排污时间后，池内粒子排除率均在95%以上；

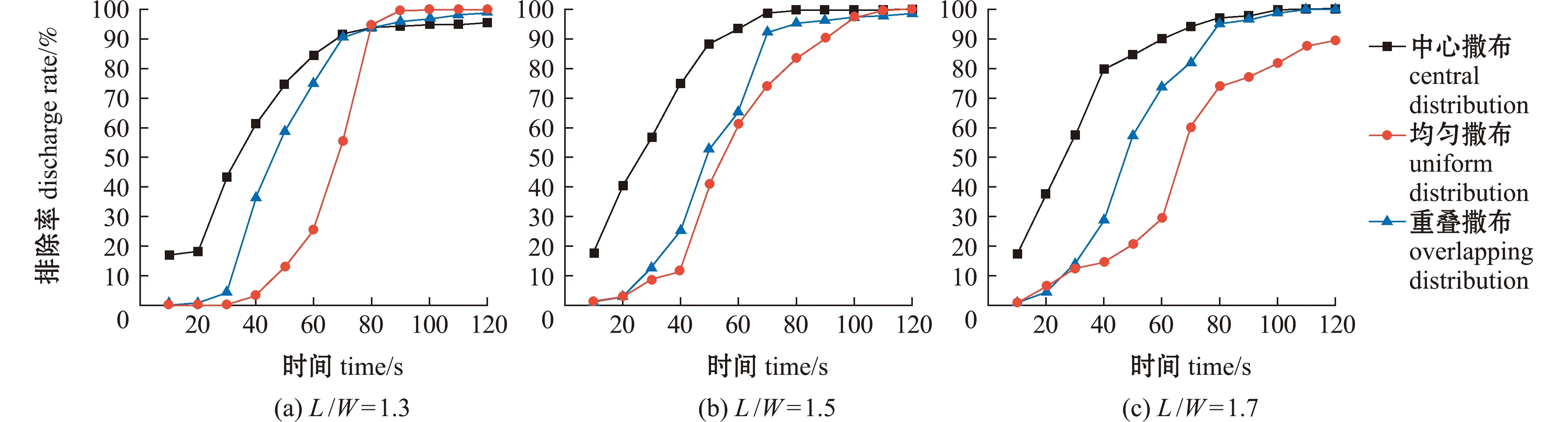
图8 进水管布置在宽边时3种撒布方式的粒子排除率Fig.8 Particle discharge rate at three spreading modes when the inlet pipes are disposed under wide edge condition

在L/W=1.7的养殖池中，中心撒布、重叠撒布方式在规定排污时间内粒子排除率无明显下降，而均匀撒布方式粒子排除率下降了8%。从图9可以看出，随着长宽比的增加，养殖池内水体的环流形态由圆形过渡为椭圆形，池内边角位置出现低流速区，结合图8可以看出，在3种不同长宽比工况下，中心撒布方式工况池内粒子的排除效率最高，均匀撒布方式池内粒子的排除效率最低。由此可见，重叠撒布方式既具有粒子分布的均匀性，又拥有较高的粒子排除效率，故在后续研究中均采用此粒子撒布方式。

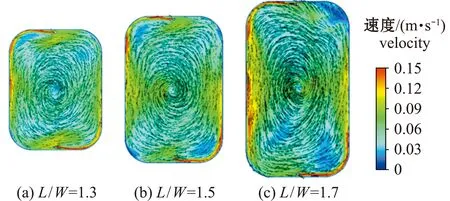
图9 进水管布置在宽边时3种长宽比工况的流场速度分布云图Fig.9 Cloudchart of flow field velocity distribution at three length width ratios when the inlet pipes are disposed under wide edge condition

2.2 进水管布置在宽边时不同工况的池内排污效果

本研究中模拟了120 s排污时间内，在L/W=1.0～1.9工况下养殖池内粒子的排除效果。从图10可见，L/W=1.0～1.7工况下，养殖池具有较好的排污效果，粒子排除率在98%以上，并且各工况下粒子排除率相近。为进一步分析养殖池的排污效果，图11给出了各工况下，不同排污时间点时养殖池内粒子分布情况和距池底0.02 m水平面的流速分布。从图11可见：在L/W=1.0～1.7工况下，养殖池具有较高的整体平均流速，粒子能够快速汇聚到养殖池中心区域并且被快速排除；随着长宽比的增加，在L/W=1.8工况下，养殖池内出现了较大面积的低流速区，虽然最终粒子排除率可达95%，但排除效率明显下降；在L/W=1.9工况下，养殖池整体平均流速明显低于其他工况，池内大部分粒子滞留在中心低流速区，无法排除到池外，池内排污效果较差。

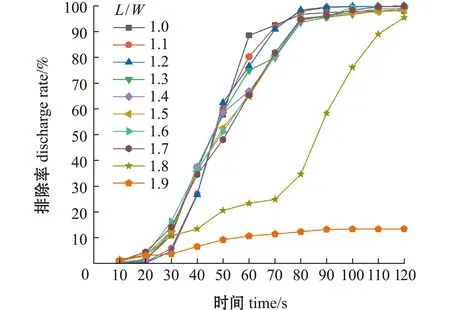
图10 进水管布置在宽边时不同长宽比工况的粒子排除率Fig.10 Particle discharge rate at different length width ratios when the inlet pipes are disposed under wide edge condition

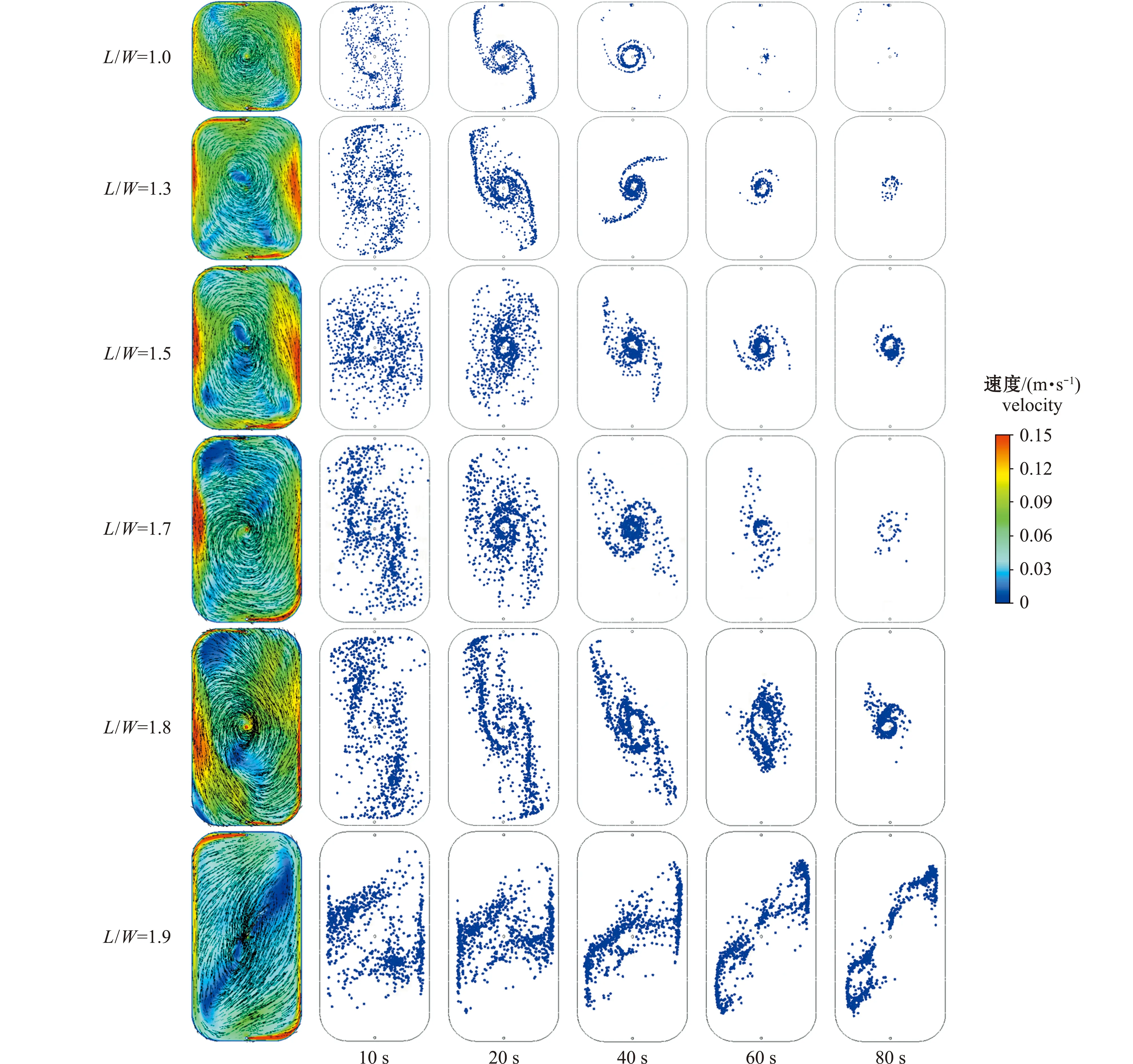
图11 进水管布置在宽边时不同长宽比工况的粒子分布形态Fig.11 Particle distribution pattern at different length width ratios when the inlet pipes are disposed under wide edge condition

2.3 进水管布置在长边时不同工况的池内排污效果

综合进水管布置在长边时，各工况下养殖池内粒子排除率(图12)，以及不同排污时间点养殖池内粒子分布和距池底0.02 m水平面的流速分布图(图13)可以看出：在L/W=1.0～1.5工况下，养殖池内具有较好的环流流场和较高的整体平均流速，养殖池内粒子能够快速排除，最终排除率可达96%以上；在L/W=1.6～1.8工况下，由于养殖池内低流速区面积的增加，粒子向养殖池中心汇聚速度变慢，最终粒子排除率下降至82%，较L/W=1.0～1.5工况时下降了14%；在L/W=1.9工况下，池内低流速区面积比例继续增加，池内粒子呈不规则长条状分布，汇聚到中心区域的粒子数量较少，粒子排除数量较少，排污效果变差。

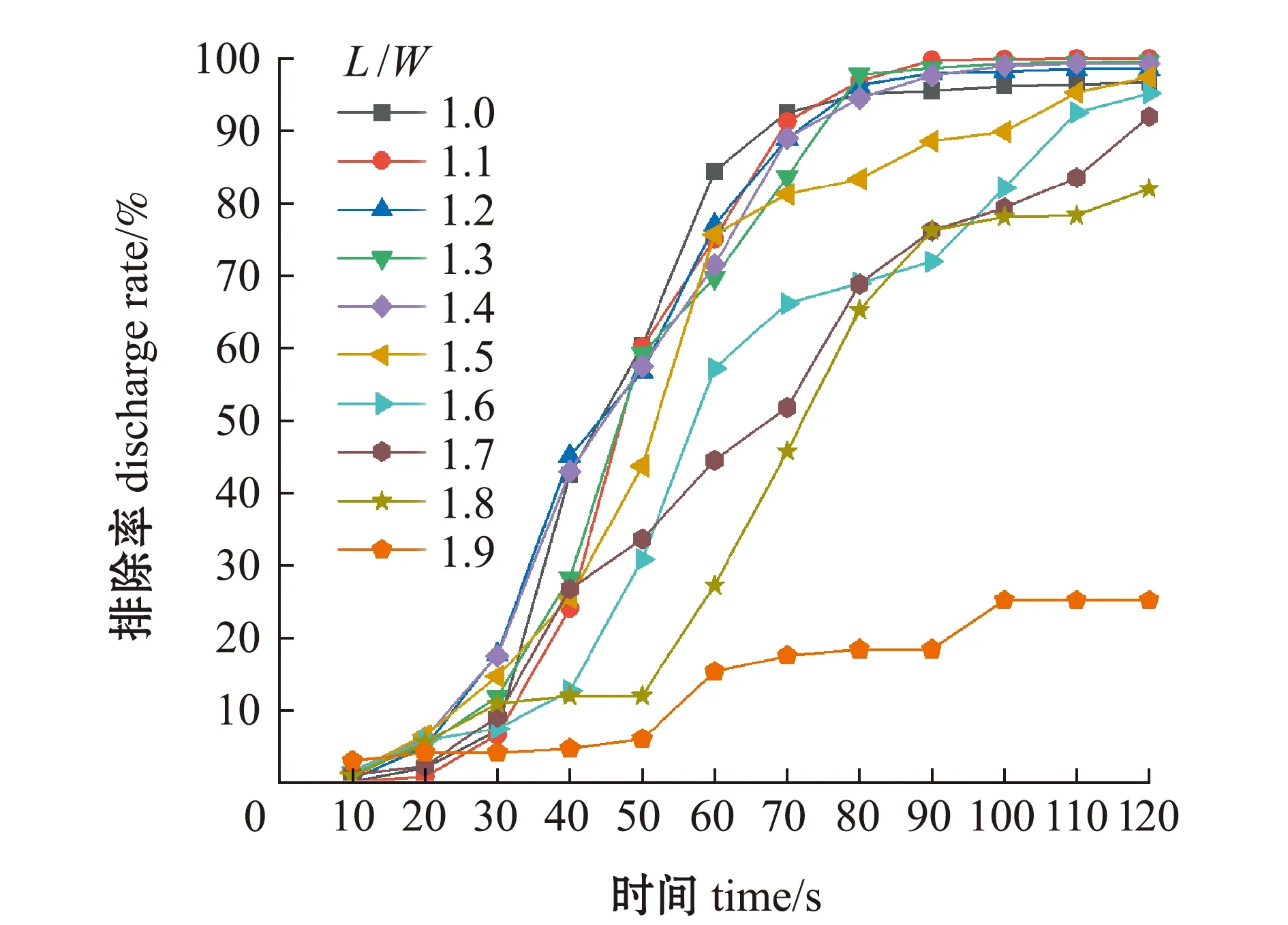
图12 进水管布置在长边时不同长宽比工况的粒子排除率Fig.12 Particle discharge rate at different length width ratios when the inlet pipes are disposed under long side condition

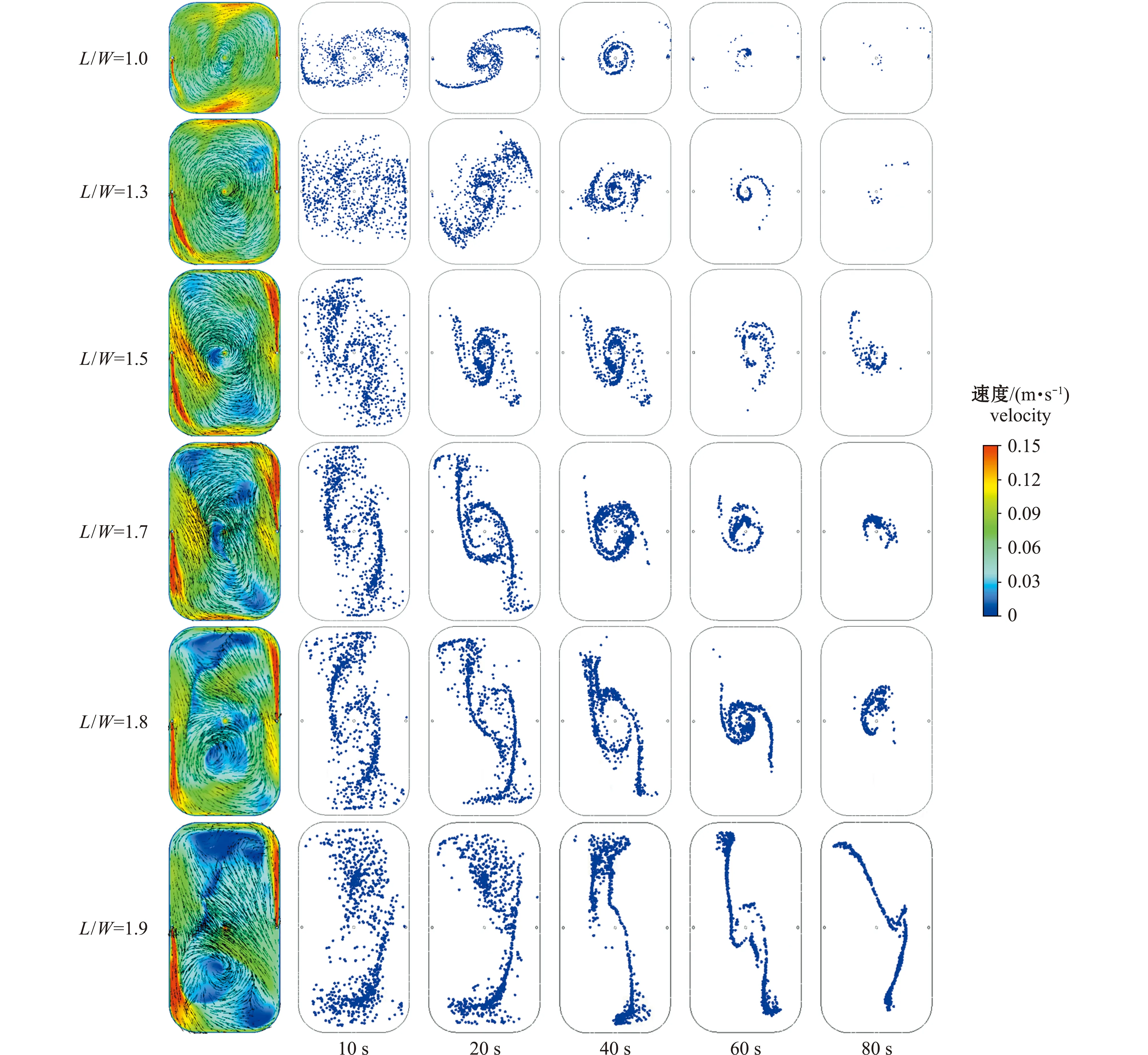
图13 进水管布置在长边时不同长宽比工况的粒子分布形态Fig.13 Particle distribution pattern at different length width ratios when the inlet pipes are disposed under long side condition

2.4 两种进水管布置方式下池内粒子排除效果的比较

将两种不同进水管布置方式及各工况下池内粒子排除效果对比可以看出，在L/W=1.0～1.5工况时，两种进水布置方式下池内粒子排除率大体一致，排污效果良好；在L/W=1.6～1.8工况时，进水管布置在宽边时粒子排除率高于布置在长边时；在L/W=1.9工况时，两种进水布置方式的排污效果均欠佳，但进水管布置在长边时池内粒子聚集情况更好。

3 讨论

3.1 粒子撒布方式的优化

使用固-液两相流数值模型模拟养殖池排污效果时，撒布粒子是进行DPM离散计算的关键步骤之一，粒子的撒布方式直接决定了粒子的投放位置，对模拟养殖池的排污效果会产生较大的影响。在以往的矩形圆弧角、矩形切角和八角形等养殖池排污数值模拟研究中，由于养殖池池形相对固定，多采用在池中心撒布粒子的中心撒布方式，但此粒子撒布方式对较大长宽比养殖池排污模拟效果欠佳。为了更好地进行较大长宽比养殖池的排污模拟计算，本研究中定义了两种新的粒子撒布方式，即均匀撒布和重叠撒布。这两种撒布方式比中心撒布方式扩大了粒子的撒布面积，更贴近实际养殖池中粒子分布状况。重叠撒布方式部分粒子分布在养殖池水体速度矢量线密集、速度较高的两进水管轴线上，这种分布有利于粒子向池心区域移动；而均匀撒布方式粒子在养殖池边角位置分布的比例较大，在较大长宽比的池形中，边角区域存在较大面积的低流速区，并且该区域内水流方向杂乱，使得粒子向中心区域移动困难，粒子的排除率有所下降，导致均匀撒布方式的粒子排除率低于中心撒布方式和重叠撒布方式。由以上分析可知，重叠撒布方式弥补了中心撒布方式无法模拟较大长宽比养殖池中边角位置粒子排除效果差的缺陷，提高了粒子撒布的空间分布均匀性，保持了与中心撒布方式相近的粒子排除率。因此，在研究不同长宽比矩形养殖池排污模拟计算中，采用重叠撒布方式不仅更贴近实际工况，而且计算结果精度更高。

3.2 长宽比对矩形圆弧角养殖池内排污特性的影响

在矩形圆弧角养殖池的排污特性模拟研究中，较少有学者关注长宽比参数对养殖池内排污效果的影响，随着长宽比的增加，池形由方形逐渐向矩形过渡，养殖池内流场的流态、能量和均匀性等均会产生变化[26]，养殖池的排污效果也会产生差异。为探究具有较好排污性能的长宽比区间，本研究中对双进水管分别布置在长边和宽边时不同长宽比养殖池的排污效果进行了模拟，结果表明，养殖池内流场的流态对排污效果的影响较为明显，这一结论与Gorle等[14]的研究结果一致。当L/W=1.0～1.5时，养殖池内流态呈现规则的圆形或椭圆形环流形态，在边角位置水流的导向作用较强，低流速区占比较小，池内粒子在水流的驱动下能够高效地排除；随着长宽比的继续增加，池内边角区域出现大面积的低流速区，使得池内水体环流形态不规则，水体流动杂乱，对粒子向池心移动的驱动能力减弱，导致养殖池排污效果下降。综上可知，长宽比变化对养殖池排污效果有较明显的影响，在L/W=1.0～1.5时，养殖池具有良好的排污性能，同时还可以满足建设场地的要求。

4 结论

1)在同一排污时间节点时，本研究中建立的固-液两相流数值模型与物理模型试验计算的养殖池内粒子排除率差值在3%以内，表明该数值模型能够很好地模拟养殖池排污效果，并且具有较高的计算精度。

2)本研究中定义了与中心撒布方式粒子排除率相近的兼具粒子撒布均匀性的重叠撒布方式，这种粒子撒布方式更贴近实际养殖池中粒子分布状态，能够较好地模拟较大长宽比养殖池的排污效果。

3)在本研究范围内，L/W=1.0～1.5工况下，两种进水管布置方式的养殖池排污效果均较好，粒子排除率达95%以上；随着长宽比的增加，养殖池的排污性能逐渐变差。在实际工程建设矩形圆弧角养殖池时，可参考本研究结果选择合适的长宽比构建养殖池。