基于传统CNN-LSTM模型和PGAN模型的用电量预测对比研究

陈露东,卢嗣斌,徐常

(贵州电网有限责任公司电网规划研究中心配网规划室,贵阳 550003)

0 引 言

随着时代变迁,人工智能在半个世纪的时间内曲折前进。大量的学者认为,在计算机时代,整个世界将进入人工智能时代[1]。随着工业和人民生活水平的提高,对电力能源的供应量和供应效率都提出了更高的要求[2-4]。“智能电网”一词大量出现在各大期刊和出版物上,已经引起了国内外学者的广泛关注[5-6]。并且,在全球倡导绿色低碳,可持续发展的大背景下,智能电网已经从广大学者的想法中找到了一条可行的道路,与人工智能相结合,应对设计和建设智能电网的挑战。未来的智能电网是将信息和通信纳入发电、输电和消费的各个方面,尽量减少对环境的污染,增强电力能源的利用效率,降低成本的同时增强可靠性[7]。在智能电网发展下,大多数的电力问题通常都源于配电系统。其组件数量庞大,运行和控制相对缓慢需,并且需要较高的资本进行维护。配电网智能化升级是智能电网发展的核心,其中用电量的预测被认为是关键一步[8]。目前,传统电网是一个刚性系统,电能的传输、储存和分配等都缺乏弹性[9],使得传统电网存在着效率低,电能浪费严重,信息交互能力弱和自动化程度低的缺点[10-11]。

以时间序列和回归分析法为代表的传统方法中,利用混沌时间序列方法进行了短期内的用电量预测[12]。此外还有研究表明稀疏惩罚分位数回归分析在短期用电量预测内有着显著的成效[13]。虽然传统的预测方法能达到不错的效果,但受到多种因素的共同影响,无法获得精确的预测。近些年来以深度学习为代表的前沿智能学习方法运用在用电量分析的过程中,其无需建立准确的数学模型,就可以抽象出时间序列的特征。其中长短时记忆神经网络在用电量领域已经有所研究,但其仍然处于预测方法的初级阶段[14]。还有学者通过改进粒子群算法,依据不同粒子惯性权重选择小波神经网络寻优策略进行用电量预测[15]。然而在实际用电量预测中,对于复杂对象的用电量预测,单一测算法仍存在着很大的局限性。在统筹全局的情况下,选择合适的智能算法,并且在权衡计算资源耗费的同时,达到用电量预测的最高效化。

一晃二十年过去了，他看着易非的父亲从楼上跳下来，看着易非的母亲处理丧事，看着易非求学和长大。他们都没有断联系。他觉得易叔就像一棵被雷劈火烧过的树木，死了，但枝干还在，怒指苍穹，易非从死干上长出新枝，而长得愈发的急迫和顽强。对，就是急迫，就是这种感觉，可惜田有园表达不出来。

以产业园区用电量为例,分析两种被广泛应用的时间序列预测方法(自回归模型和长短时记忆网络模型),并提出了生成对抗网络模型进行用电量预测。对比了三种智能算法在产业园区用电量预测中的效果,所得结果未来可以用于各大电网发电量、输电量和损耗等预测。同时根据三种预测方法的效率和计算量,设计一套智能电网自动控制系统,对几种方法进行合理高效的分配。将智能用电量预测和智能调控相结合,将大大地减少电力损耗,实现绿色可持续发展。

1 预测算法

介绍了对用电量预测的方法,其中包括自回归模型预测,卷积神经网络与长短时记忆网络预测,和生成对抗网络预测模型。这在结果章节对比这些智能算法所得结果。

1.1 自回归方法

运用了差分整合移动平均自回归模型(ARIMA),进行时间序列预测从而达到对用电量的预测。ARIMA是典型的时间序列模型之一,由三部分组成:自回归模型(AR);滑动平均模型(MA)和差分阶数(I)。

其中AR模型为:

yt=a0+a1yt-1+a2yt-2+…+apyt-p+εt

(1)

式中y1,y2,y3,…,yt为一个时间序列;p为自回归阶数;εt是均值为0,方差为σ2的白噪声序列。值得注意的是,为满足平稳性条件,要满足|a|<1。

MA模型为:

yt=c+εt+θtεt-1

(2)

GAN用于时间序列预测问题,实质为生成器和鉴别器不停对抗的过程中,预测值不断的逼近真实值,实现预测。生成器的输入包括两个方面,用电量数据的时间序列的概率分布和噪声向量。鉴别器中输入用电量数据和单步预测的标签(真实观测数据)。

自回归移动平均模型(ARMA):

yt=c+a1yt-1+a2yt-2+…+apyt-p+εt+θ1εt-1+

θ2εt-2+…+θqεt-q

(3)

MA滑动平均过程在任何情况下都是平稳的,由于AR需满足平稳性要求,故ARMA同样要满足平稳性要求:即等式的根均分布在单位圆外。如果存在有跟落在单位圆上,则此时的ARMA(p,q)过程称为差分自回归移动平均过程(ARIMA(p,d,q))。

在预测前,首先设计了三种简单的方案进行初步预测,作为预测结果的对比标准,方案一为将一周前同期的用电量作为预测值,方案二为将一月前同期的用电量作为预测值,方案三为将一年前同期的用电量作为预测值。从测试集中随机抽取一周数据,分别应用三种方案所得结果如图4所示,根据计算均方误差的结果可以看出,三种方案存在着明显的差异,其中方案三的效果最好,方案一、二效果接近,这可能与季节气候变化、节假日安排和经济状况有着一定的关系。方案三效果较好,但是总体均方误差仍处于较大的水平(均方根误差>450),只能大致预测用电量变化,难以精确预测。将这三组数据作为预测结果的比较标准,对三种不同的算法进行评估。

yt-yt-1=(a-1)yt-1+εt

(4)

Δyt=yt-yt-1=(a-1)yt-1+εt

(5)

Δ(Δyt)=2yt=(yt-yt-1)-(yt-1-yt-2)

(6)

在ARIMA模型中,差分运算的作用是使得时间序列恢复平稳。

1.2 长短时记忆网络预测

条件生成对抗网络(CGAN)是GAN的一个扩展,它使模型限定在一些额外的信息y上,y可以是任何类型的辅助信息。因此设置的新值函数为:

在时间序列处理的研究中,LSTM网络是一种十分常用的时间递归神经网络(如图1所示)。其通过引入记忆单元对传统的递归神经网络(RNN)进行了升级。其内部主要包含三个步骤,首先是忘记步骤,通过忘记门σf对上一时刻的输入状态ct-1进行控制,过滤不重要的信息。其次是选择阶段,通过选择门的控制信号σi来记录有用信息。两个步骤所得结果为当前状态ct。最后一步为输出,通过控制信号σo对输出门进行控制,得到最终输出ht。其中,tanh为激活函数对状态量和输入量进行放缩,X为输入的时间序列。

各地湖泊管理单位根据自身情况建立了相应的高邮湖湖泊巡查网络，完善巡查制度，湖泊巡查工作有序开展，为维护湖泊良好的水事秩序，对控制涉湖违法水事案件的发生起到了积极显著的作用。

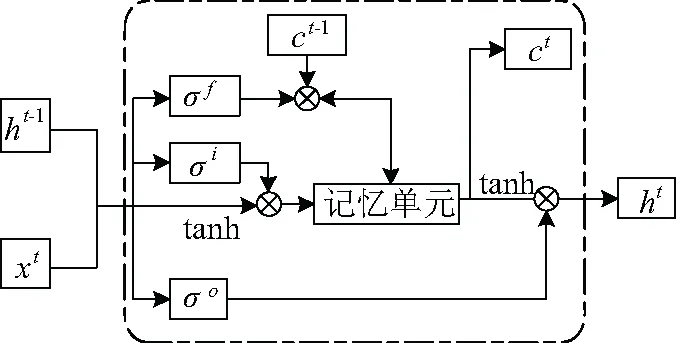
图1 长短时记忆网络(LSTM)框架图

1.3 生成对抗网络预测

近年来,生成对抗网络(GAN)被应用于序列数据领域的各种问题,并取得了显著的效果。目前GAN多用于生成听觉,图像和文字数据,但由于这些研究不涉及预测,其结果是可以被评估的[16]。 在预测中应用GAN是具有十分大的挑战,因为目前没有一个统一的评估标准。

GAN是一类从数据概率分布中给定一组样本模拟概率分布的算法,其结构如表1所示。

表1 生成对抗网络的结构

一个GAN由两个神经网络组成,即发生器G和鉴别器D,这两个神经网络在对抗过程中同时被训练。首先,从已知概率分布Pnoise(z)(通常为高斯分布)中采样噪声向量z。G以噪声矢量z为输入,训练生成一个分布服从Pdata的样本。另一方面,对D进行优化,以区分生成的数据和真实的数据。D和G用值函数进行以下两人极小极大对策:

V(G,D)

(7)

(8)

CNN是一种包含输入层、卷积层、池化层、全连接层和输出层的一种前馈神经网络,CNN网络的目的是对目标进行特征提取,通过对数据的卷积和池化处理,可以提取出隐藏在数据背后的特征关系。

Ez～Pz(z)[log(1-D(G(z|y))]

(9)

比如，当教师在讲解课文《我们爱你啊，祖国》时，便可以通过以下方式开展教学：首先，教师可以通过信息技术在网络平台上下载与教学内容相关的素材，加深学生的感受，营造合适的教学氛围。其次，教师可以为学生展示巍峨耸立的泰山、庄严肃穆的故宫以及宏伟壮丽的布达拉宫。在一幅幅动态或静态的画面中，学生能够感受到中国的伟大，同时也能够加深对祖国的热爱之情，形成一定的知识记忆。

从表2可以看出，攀枝花优质钛精矿经流态化氧化→流态化还原→常压一段流态化浸出及过滤、洗涤、干燥煅烧后，钛精矿中TiO2品位可从47%左右提高至约90%，CaO+MgO总含量从7.5%左右降至约1.5%，其中CaO含量在0.75%左右，SiO2含量5%左右，不满足大型沸腾氯化法生产钛白粉对原料的要求。为了进一步降低产品中杂质元素含量，对人造金红石产品进行了磁选试验。经磁选后人造金红石TiO2含量≥92%，CaO+MgO总含量约0.6%，其中CaO含量在0.3%以上，SiO2含量4%左右，仍高于氯化钛白原料对CaO和SiO2的指标要求。

构建体育教师教育专业化框架，首先要分析专业发展的所属范畴。专业化框架归根到底是实施主体作用机制下制度、层级、模式及相互关系的建设。构成体育教师教育专业化框架要遵循专业发展发展的基本运行机制，制度层面的设置基于体育专业标准及体育教学课程标准的教育培训制度和资格认证制度；层级层面体现出体育教师教育培训和资格认证的等级性和终身性；模式层面设置体育教师的教育培训模式和资格认证模式等。基于专业社会学的理论，可以整合出两个维度来分析体育教师的专业化框架构建的问题，且这两个维度在一定程度上包含了以上各个层面所涉及的内容。

以贵州产业园区用电量的历史数据为基础,进一步建立超前值xt+1的概率分布模型:

对发电机整体在安装弹性支撑为10kN/mm的弹性支撑时进行模态仿真分析，弹性支撑主要参数如表4和表5所示，前9阶振动频率如表6所示，其中前9阶静态刚度时振型如图3所示(由于前9阶振型一致只是频率不一致，动态刚度振型图在此省略)。

c={x0,…,xt}

(10)

P(xt+1)

(11)

使用CGAN进行模拟:

P(xt+1|c)

(12)

如图2所示,建立预测生成对抗网络模型(PGAN),历史数据作为条件提供给发生器和鉴别器。发生器从平均值为0和标准偏差为1的高斯分布中抽取噪声向量,并根据条件窗口c预测xt+1。鉴别器获取xt+1并检查它是否是跟踪c的有效值。因此,进一步更新函数为:

突然响起一波嘘声，我抬起头，看见电视屏幕上出现了首相，她的头发甚至比平日更加灰白。她站在唐宁街首相官邸外面，一身穿着和她离开前往外星人母舰时一模一样。

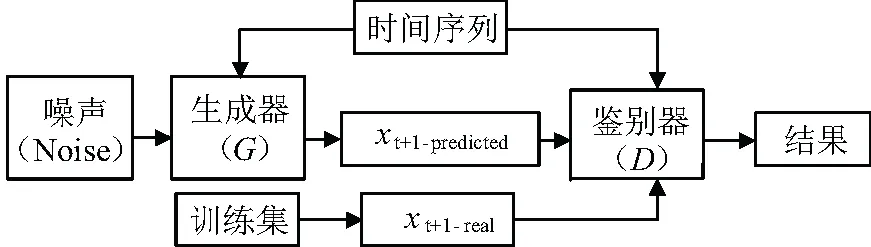
图2 预测型生成对抗网络框架图

Ez～Pz(z)[log(1-D(G(z|c))]

(13)

通过训练该模型,最优生成器对给定条件下xt+1的全概率分布进行建模。掌握了完整的概率分布后,可以通过抽样来提取关于任何可能结果及其发生概率的信息。

通常,预测模型是通过优化某一个点的状态误差作为损失函数来训练的,而GAN采用对抗性训练来训练神经网络实现预测目的。将均方根误差(RMSE)优化为损失函数来训练该模型,并将其结果与另外两种常用的预测模型的结果进行了比较。

在训练GAN时,生成器G学习将已知的概率分布Pz转换为与Pdata相似的生成器分布PG。

2 用电量预测结果分析

在智能电网覆盖城市的大背景下,对用电量进行预测,并且进行自动化调控,检测工厂、发电站和第三产业用电等。文中选取了中国贵州某产业园区3年以来的用电情况作为例子,来研究数据采集准备方法,和不同方法架构之间的比较。

2.1 数据预处理

数据集包含日期、时间信息,有功功率,无功功率,平均电压,平均电流这6个变量。对于用电量预测实验来说,数据集中的数据是不完整的,并且得到的数据集中包含了大量的异常值。两种方法可以去替换异常值:(1)利用异常值前一天和后一天同时间值的平均值代替。(2)利用一年前同时间的值代替。由于季节和节假日等因素影响,方案2的效果更加理想。每种属性以时间序列记录,其采样周期为1分钟如图3(a)。由于预测不需要做到分钟的精度,这样不仅耗费资源,浪费时间,也没有实际意义。对每段时间序列进行了降采样,以天为单位如图3(b),这样可以大大提升用电量预测的效率和实际意义。数据集中包含3年的数据,用前2年的数据作为训练集,最后1年的数据作为测试集,定义RMSE为衡量预测结果好坏的标准,RMSE值越小,说明模型预测结果越好,均方根误差值越大,说明模型预测结果越大。并且从测试集中随机抽取一周数据,来展示预测效果。

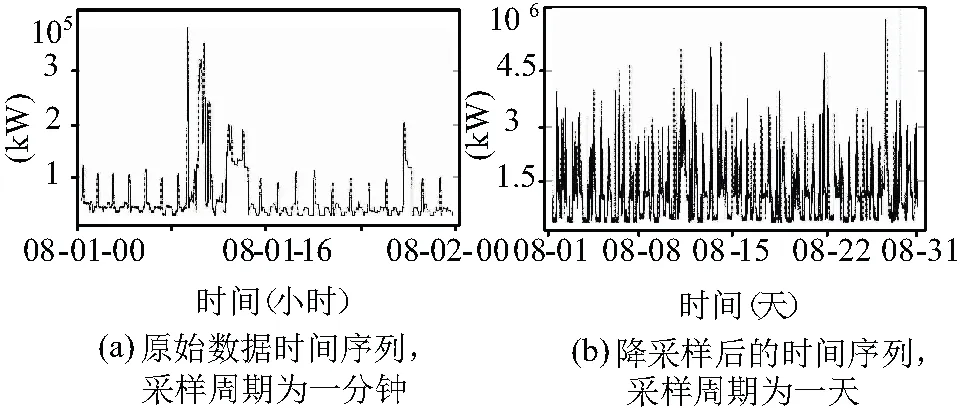
图3 数据集中的时间序列图例

2.2 建立基础预测标准

差分运算表达式:

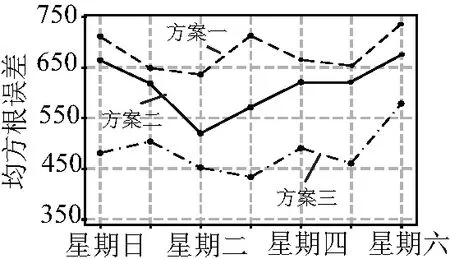
图4 简单模型方案下一周用电预测结果

2.3 ARIMA模型预测结果

使用循环神经网络(RNN)作为产生器和鉴别器的主要组成部分。图7中,生成器获取条件用电量时间序列并通过RNN层传递条件来构造其表示。然后,将条件表示与噪声向量连接起来,通过两个密集层,得到预测的t+1时概率模型(xt+1)。如图8所示,鉴别器从产生器或数据集中沿着相应的条件用电量时间序列获取xt+1,并在条件用电量时间序列的末尾连接xt+1以获得{x0,…,xt+1}。并检查时间序列的有效性。结果如图9所示,相比基础预测标准的均方根误差出现了显著的下降,如图10。GAN预测的结果优于CNN与CNN-LSTM预测结果,并且预测时间也较其有所缩短。对两类模型的均方根误差进行t检验,自回归模型的均方根误差显著低于基础预测标准(P< 0.05)。

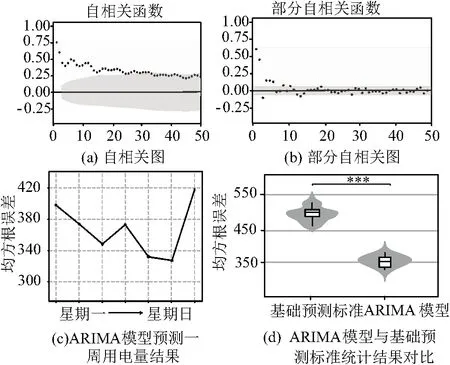
图5 ARIMA模型以及预测结果

结果如图5(c)所示,均方根误差出现了明显的下降,与基础预测标准相同的是,星期天与星期六的用电量预测值仍然误差较大。但整体的准确性得到了大幅提高,即预测天数的平均均方误差得到了显著的降低(简单模型平均均方误差约为 514,自相关函数模型平均均方根误差约为369)。如图5(d),对两类模型的均方根误差进行t检验,自回归模型的均方根误差显著低于基础预测标准(P< 0.001)。

2.4 CNN与CNN-LSTM预测结果

考虑到降采样后,训练集的数据较少。故在进行深度学习预测前,更改采样周期,放弃标准周的限定,而是对每7天的数据进行一次采样,对已有训练集进行扩充。将数据集扩大7倍。对卷积神经网络进行训练并且得出预测结果(见图6),发现CNN所得结果的确较基础预测标准有了明显提高,但是与ARIMA模型所得结果差距不大,并且训练所花费的时间也远远大于ARIMA模型所花费的时间,所以认为CNN不适合应用在用电量预测方面。相较CNN,增加了LSTM结构后,大大的增加了神经网络的预测准确率,并且两者组合的模型更加稳定,预测误差效果更加理想。卷积神经网络去提取特征,长短时记忆网络去解释这些特征。预测结果如图6所示,准确率大大提高,平均均方根误差降低到了350以下。在用电量方面有了质的飞跃。

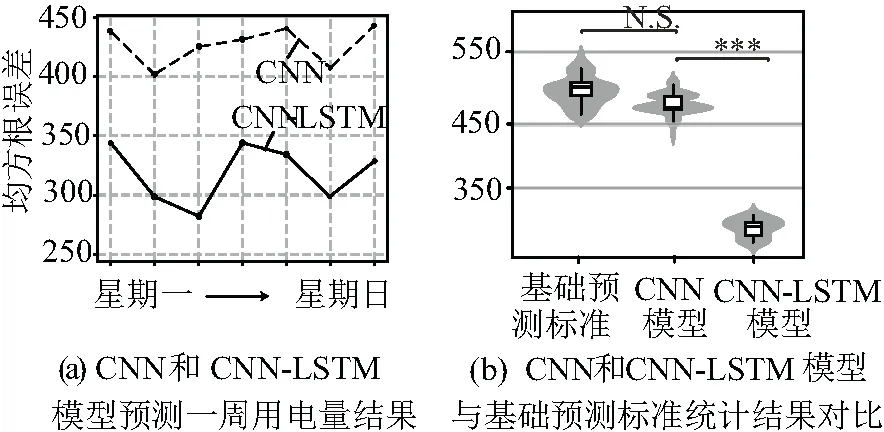
图6 利用CNN和CNN-LSTM模型预测用电量结果

2.5 PGAN预测结果

式中c表示常数项;θ表示系数。

作品以行刺秦王为题材，意在展现一群仁人志士当燕国国势迫急之际而展现出来的为信义而轻生死的精神力量，这种精神力量在与强秦以欺诈和暴虐吞并列国的行为对比中，在“势”与“道”之争中，建起了另一座价值丰碑。

首先画出自相关函数图和部分自相关函数图,来确定开始模型的滞后观测值设置,如图5(a)所示,自相关图中,发现了较为显著的滞后观测量,并且随着滞后的增加相关性逐渐减小。图5(b)中,自相关系数呈现出拖尾特征,逐渐减小,部分自相关系数的前6阶不在置信区间内,并且关注到在第7个分量处出现了明显的不同,因此选取6阶附近的几个阶数作为AR模型的阶数,然后对结果进行比较,最终选择模型为AR(7),此时均方根误差为最低。

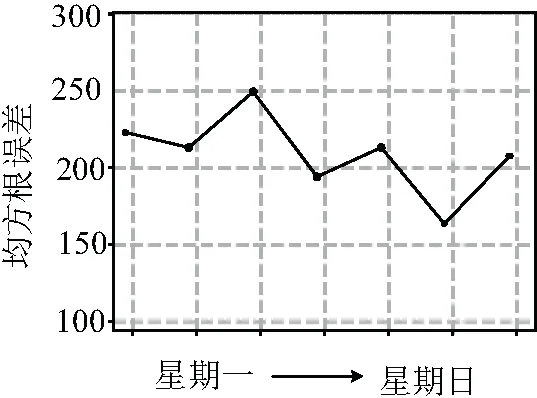
图7 生成器结构图

图8 鉴别器结构图

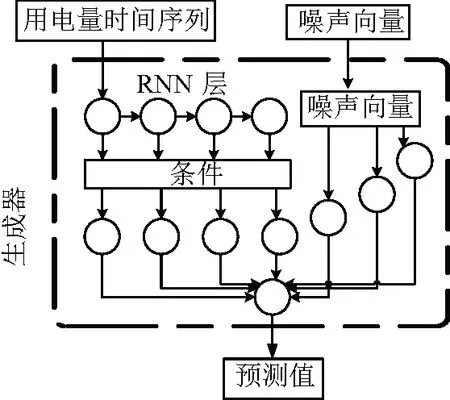
图9 GAN模型预测一周用电量结果

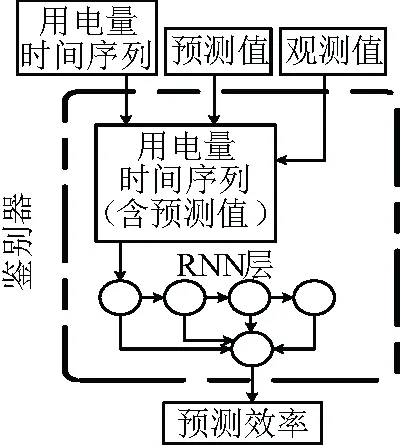
图10 CNN和CNN-LSTM模型与GAN模型统计结果对比

2.6 智能预测用电量网络设计

如表2所示,三种算法在用电量预测方面的应用各有优劣,面对的用电量预测这一个实际问题,要考虑许多现实因素。CNN-LSTM模型计算精度高,但是计算时间长,占用资源大,不适宜广泛应用于各类用电量预测。ARIMA模型精度较低,但是计算时间短,可以高效地预测大规模的用电量。GAN网络较好的综合了两者优点,训练时间较短并且预测正确率较高。

表2 用电量预测RMSE平均值结果比较

在智能电网的大背景下建立用电用户自动筛选系统,在该系统中集成ARIMA模型,CNN-LSTM模型和GAN模型,利用ARIMA对智能电网下各类用电量进行初步预测,根据用电用户重要性和优先级选择用电量预测方法。并且建立反馈通路,将预测的结果与实际的比较结果作为校正值反馈给模型,如果遇到误差持续过大的情况,可以利用更高级的模型进行计算,并且对其进行校正,这样大大提高了用电量检测的效率。图11中的流程图,是根据对方法的研究,设计的多算法融合用电量预测系统。根据算法的复杂程度将预测的模型分为初级模型,中级模型和高级模型。从智能电网数据库中读取各类用电量数据,并与安装在终端的智能传感器采集的环境数据结合,生成用电量历史数据集,对用电用户进行评估,分别用三种模型进行预测,对于一些不间断用电的用电用户,可以直接给出预测值。预测值发送到智能配电网和智能发电厂进行电力资源的调配。同时,设计一个反馈系统,从智能电表上采集实时用电量,与预测值进行比较,反馈误差来对系统进行自动调控。

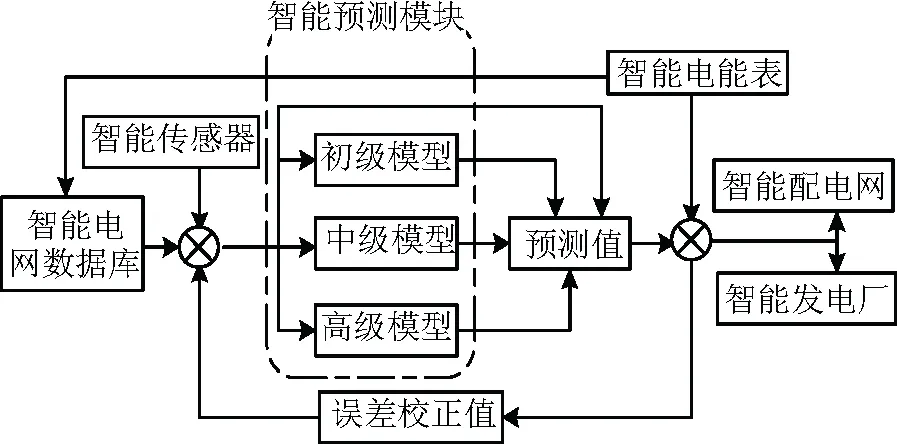
图11 智能电网中预测用电量流程图

从现有数据集中选择产业园区连续6个月的用电量,并且按照不同类型(工业用电,生活用电和基础设施用电)的用电量分为三组,分别模拟国家依据可靠性要求分为三类符合用户对象:一类用户(突然中断供电将会造成人身伤亡或会引起周围环境严重污染的,将会造成经济上的巨大损失的,将会造成社会秩序严重混乱或在政治上产生严重影响的用户)、二类用户(突然中断供电会造成经济上较大损失的,将会造成社会秩序混乱或政治上产生较大影响的用户)、三类用户(不属于上述一类和二类负荷的其他用户)。以第1个月的数据作为数据集,后5个月为测试集。对提出的智能预测用电量网络测试。按照用电量的等级,选择相对应的预测方法,并且对结果进行评估。提出一个效率评价指标E,它等于均方根误差与时间的乘积的倒数。在实际试验中,随着数据量的增加,平衡时间与准确性,智能用电量预测模型的效率评价指标越高,并且显著的高于使用单一预测方法的效率评价指标。故所提出的智能预测用电量网络为未来智能电网下的用电量规划提供了一种新的思路

基于无公害中药选肥原则：选用国家生产绿色食品的肥料使用准则中允许使用的肥料种类，所有的肥料应以对环境和作物不产生不良后果的方法使用。黄芩施肥应坚持以基肥为主、追肥为辅和有机肥为主、化肥为辅的原则。有机肥包括高温腐熟、杀菌处理后的堆肥、厩肥、沼肥、绿肥、作物秸秆、泥肥、饼肥等；生物菌肥包括腐殖酸类肥料、根瘤菌肥料、磷细菌肥料、复合微生物肥料等；微量元素肥料即以铜、铁、硼、锌、锰、钼等微量元素及有益元素为主。

3 讨论

当下,很多研究者对智能电网展开研究。结合物联网、大数据和智能算法等,已经做出了十分多的用电量预测方案[17]。有研究者提出基于多表融合的方法对用户短期用电量进行预测,将水、电、气三表数据合一,利用机器学习算法对用户用电量做出了预测,得到十分理想的效果[16,18-19]。

用电量预测已经成为智能电网规划中重要的一环,其发展关系到智能电网的建设以及城市的发展。本文利用了ARIMA模型、CNN-LSTM模型和PGAN模型对用户用电量进行预测,并对其在用电量预测中的效果进行了评估,结合各类方法的特点,提出智能电网中用电量预测具体的实现模型。并且对未来的智能电网的部分系统结合用电量预测模块设计出控制图,具有很理想的实际意义。

4 结束语

文章主要研究生成对抗网络等模型在用电量预测方面的应用。综合各类算法的优劣,设计了用电量预测系统,并将该系统运用在智能电网系统中。为智能电网动态规划和优化提供了新的思路和方法。对产业园区用电数据进行预测,得出结论:

总体而言，对人的主体性关切已经成为学界阐释马克思实践观的核心入路，在这一基础上，研究者们从不同的视域进行了各具特色的诠释。以上所述关于实践的本体论、价值论、人类学等不同视域对马克思实践范畴的理解和阐释充分说明了马克思实践观在马克思哲学体系中的核心地位，就此而言，对马克思实践范畴的理解从根本上影响着研究者对整个马克思哲学的认识和把握。

(1)创新性的将生成对抗网络运用在用电量预测中,并且在用电量预测中有着很好的效果。

所谓防风固沙林，是指以通过降低风速，防止或者减缓风蚀、固定沙地，保护耕地、果园、牧场等以及农作物免受风沙侵袭为主要目的，而营造的乔木林和灌木林。如：油松、樟子松、杨树、柽柳、橡栎、山杏、白蜡、紫穗槐、沙棘、荆条、梭梭、胡枝子等等。

但考虑到训练时间和对计算资源的占用,这种算法并不适合运用在全面的用电量预测中;

2017年省级党委和政府扶贫开发工作成效考核反馈广西的问题清单中，关于扶贫资金使用管理的问题共有12项，直接点名的有马山、田东、宁明等10个县(市)。上述各县(市)对整改工作责无旁贷；其他市、县也要摆正心态，根据中央和自治区检查反馈的问题，主动对号入座，对本地区脱贫攻坚工作开展全面自查自纠，形成问题清单。各市、县要以问题清单为线索，深入分析导致问题的主观原因、制度原因、作风原因，真正把问题找全、把根源找准，做到精准整改，重点突破，确保问题全面整改到位。

(2)针对未来智能电网中用电用户的复杂程度、规模旁大和优先级顺序等特点,设计智能用电量预测系统,对不同的用电用户加以区别,分别采用不同种类的预测方法,使得实验效率最优化。

文中不仅将生成对抗网络应用在用电量预测中,更在智能电网的规范发展上提出了一种高效精准的用电量预测方案,可以结合环境、政策和经济等因素变化,实现良好的自我调节。并且对于用电量的预测从侧面也可以很好地把握国家的宏观经济调控和走势,使得国家可以及时对发展战略进行调整,掌握产业发展特点。