硫酸铵分解过程及其热分解动力学研究

吴 迪，李来时，王俊凯，吴玉胜，王昱征，李明春

（沈阳工业大学材料科学与工程学院，辽宁沈阳 110870）

硫酸铵来源于各种工业副产品，例如生产己内酰胺和火力发电厂的脱硫［1］等。硫酸铵是优良的氮肥，可提高果实的品质和产量［2］。硫酸铵也用作采矿的原料，通过离子交换提取土壤中的稀土元素［3-4］。然而，由于尿素行业的快速崛起，硫酸铵化肥的市场需求大幅下降。同时，由于中国的需求量和出口量减少及工业的快速发展，硫酸铵的累积量正在增加［5］。因此，如何将过剩的硫酸铵更好地资源化利用成为目前急需解决的关键问题。

本课题组以硫酸氢铵溶液浸出粉煤灰提取氧化铝工艺为研究背景，针对此过程中的副产物硫酸铵开展热分解过程的研究，使硫酸铵分解形成一定浓度的硫酸氢铵溶液和氨水直接返回到整个浸出过程进行循环使用，使整个工艺实现闭环，降低原料的使用率从而降低生产成本。

硫酸铵的热分解是典型的固体分解反应，然而，在以往的研究中关于硫酸铵分解的结果一直不一致。KIYOURA 等［6］使用X 射线衍射（XRD）和差热分析（DTA）研究硫酸铵的热分解过程，结果表明硫酸铵的分解分为3个步骤进行。HALSTEAD通过化学分析方法证实硫酸铵的分解过程分为2 个阶段［7］。尽管如此，对焦硫酸铵的检测手段还不够完备，而且焦硫酸铵的热分解产物也存在争议；氮气的来源也一直存在分歧，氮气［8］可能来源于硫酸铵在高温下加热时产生的酸式盐的分解，也可能由产生的硫酸氢铵转化而得到的氨基磺酸分解而得。硫酸铵与金属氧化物反应生成硫辅助金属氧化物——一种新型的固体酸催化剂［9-11］。硫酸铵与金属氧化物反应产生相对稳定的中间产物，当中间产物继续加热时会分解生成各种气体和金属氧化物。为了更好地了解硫酸铵的热分解性能，有必要对硫酸铵的热分解过程进行研究。

本课题组通过X 射线衍射（XRD）、傅里叶变换红外光谱（FT-IR）、热重-差热分析（TG-DTG-DTA）、质谱（MS）来系统研究硫酸铵热分解的反应机理，使用无模型方法获得硫酸铵热分解的活化能，使用Coats-Redfern 方法确定硫酸铵分解每个阶段最可能的机理函数。

1 实验部分

1.1 实验原料

硫酸铵为分析纯，在使用前在玛瑙研钵中研磨至少10 min，然后在373.15 K的真空烘箱中干燥5 h。

1.2 表征方法

采用XRD-7000型X射线衍射仪（XRD）分析样品的物相组成。操作条件：2θ为5°～70°，扫描速率为4（°）/min。采用IF S66V型傅里叶变换红外光谱仪（FT-IR）分析不同烧结温度下样品的官能团组成，使用KBr 压片法。采用SDT-Q600 型同步热分析仪对样品进行热重-差热分析（TG-DTG-DTA），用于研究样品的热分解动力学：样品质量约为8 mg，升温速率分别为4、6、8、10、12 K/min，温度范围为423.15～773.15 K，气氛为氮气，流速为100 mL/min。采用thermo plus EV2 质谱仪（MS）研究样品在分解阶段产生的气体并获得气体数据。

2 结果和讨论

2.1 硫酸铵热分解过程

图1 为硫酸铵在氮气气氛中以4 K/min 的升温速率分解得到的TG-DTG-DTA 曲线。从图1 看出，根据DTG 的值整个硫酸铵的分解过程分为3 个阶段，DTA 的峰方向表明所有的反应都是吸热反应［12］。其中，第一阶段的反应温度为516.15～＜597.15 K，质量损失率为14.2%；第二阶段的反应温度为597.15～＜614.15 K，质量损失率为5.78%；第三阶段的反应温度为614.15～698.15 K，质量损失率为80.02%。

KIYOURA 等［6］发现氨基磺酸和硫酸氢铵的混合物在483.15 K时会生成焦硫酸铵。而本研究在硫酸铵的热分解过程中没有发现氨基磺酸的存在。当硫酸铵加热至613.15 K 以上时，将产生的样品快速冷却并储存在干燥环境中，对此样品进行物相分析，发现存在焦硫酸铵。图2为硫酸铵在不同温度下加热所得样品的XRD 谱图。从图2看出，硫酸氢铵是在583.15 K加热后形成的。

图3 为硫酸铵在不同温度下加热所得样品的FT-IR 图。从图3 看出，在3 600 cm-1处的伸缩振动峰是由于硫酸氢铵吸水引起的；在3 000～3 300 cm-1有一个更强更宽的吸收峰，该吸收峰的出现是由于NH4+的伸缩和反对称伸缩振动及羟基（O—H）伸缩振动的共同作用引起的［13-14］，因此呈现出强而宽的峰；在1 400 cm-1处的尖锐峰是由NH4+的反对称变角振动形成［15］。从样品的FT-IR图看出，在1 400 cm-1处的吸收峰一直存在，说明NH4+存在于整个反应过程的各个阶段。

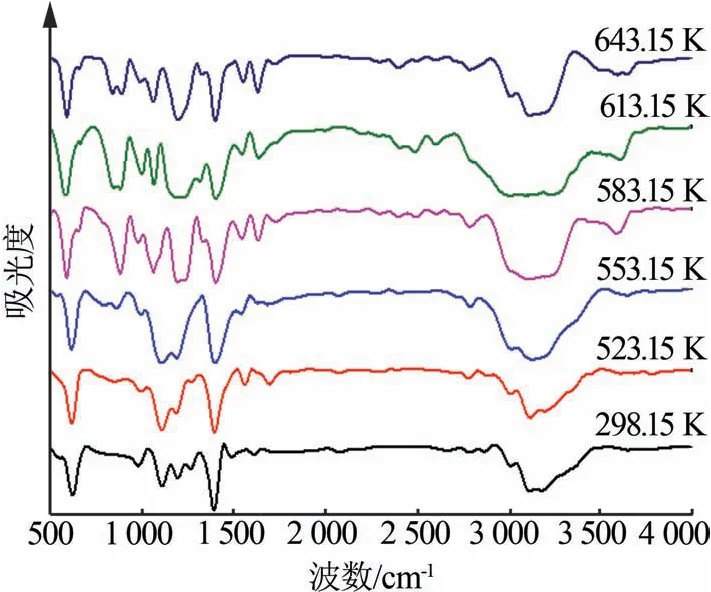
图3 硫酸铵在不同温度下加热所得样品的FT-IR图Fig.3 FT-IR spectra of samples obtained by heating ammonium sulfate at different temperatures

从图3 看出，在温度从298.15 K 升至643.15 K的过程中，样品在1 400 cm-1处的NH4+的反对称峰向高频方向移动。其主要原因为样品中的SO42-向HSO42-和S2O72-转变，由原来的强酸弱碱盐转变为弱酸弱碱盐，硫酸根内部的化学键转变成其他的形式，这种变化也与图2 中随着温度升高硫酸铵发生的物相变化相对应。当温度升至553.15 K 时，样品在1 080～1 200 cm-1处的宽峰也是由于SO42-的转变引起的。样品在1 100 cm-1处的原始吸收峰是由游离SO42-伸缩振动引起的。随着SO42-的跃迁［16］，S—O单键逐渐向高频方向移动，从而使得S—O键周边化学环境更复杂，在该区域形成宽峰，双键向低频方向移动，从而使583.15 K 时此处的尖峰变为宽谱带和多个分离峰。

从图2 发现，从298.15 K 的原料硫酸铵到613.15 K的硫酸氢铵再到643.15 K的焦硫酸铵得到比较纯的物相，可以较好地对应热分解质量损失的3个阶段。从图2发现存在硫酸氢三铵，在室温下将相同质量的硫酸铵和硫酸氢铵混合研磨，很容易生成硫酸氢三铵。硫酸氢三铵加热易生成硫酸氢铵，可以看出硫酸氢三铵是一种中间产物。由图2和图3 推测在硫酸铵的烧结过程中可能会发生以下反应，见式（1）～（6）。图4 为反应（1）～（6）的吉布斯自由能随温度的变化。

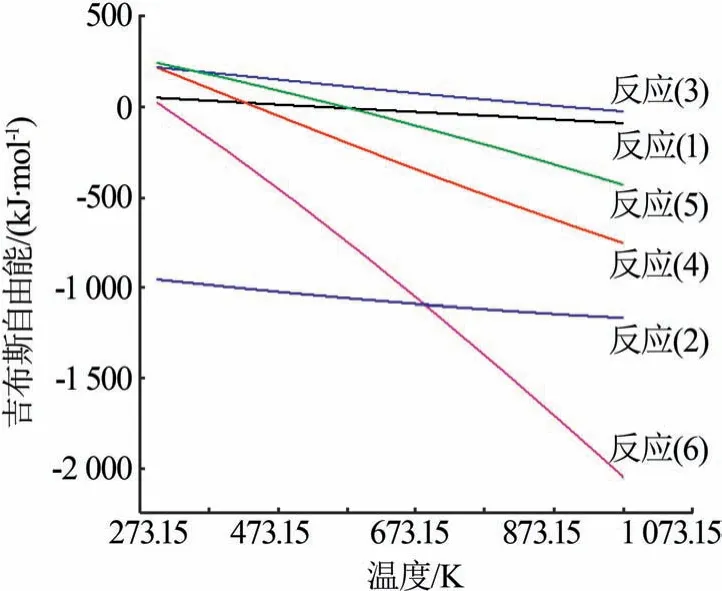
图4 反应（1）～（6）的吉布斯自由能随温度的变化Fig.4 Gibbs free energy for reactions（1～6）as a function of temperature

基于上述反应方程式进行热力学计算。根据XRD 产物和图4 中反应方程式的吉布斯自由能，得出结论反应（1）（2）（6）最有可能发生。

图5 为硫酸铵分解产生气体的MS 图。从图5看出，硫酸铵分解过程中主要产生了NH3、H2O、SO2、N24 种气体。反应（1）（2）（6）产生的气体与图5 中MS 检测到的气体一致。在整个分解过程中样品的质量损失可归因于这4种气体的释放。结合前面的分析可以看出：第一阶段的质量损失可归因于NH3的释放，主要发生的反应为反应式（1）；第二阶段的质量损失可归因于H2O 的释放，主要发生的反应为反应式（2）；第三阶段的质量损失可归因于NH3、H2O、SO2、N2的释放，主要发生的反应为反应式（6）。

表1为硫酸铵热分解质量损失率实验值与理论值对比。由表1 可看出，硫酸铵热分解质量损失率实验值与理论值对比略有偏差。原因可能是各个反应阶段之间存在交叉行为，即第一阶段的反应没有完全完成，第二阶段的反应已经开始，第二阶段还没有完全分解，第三阶段就已经开始了，因此造成了实验值和理论值不完全一致。

表1 硫酸铵热分解质量损失率实验值与理论值对比Table 1 Comparison of experimental value and theoretical value of mass loss in thermal decomposition of ammonium sulfate

2.2 硫酸铵的热分解动力学

由于反应的交叉性和连续性，硫酸铵热分解动力学的研究是复杂的。因此，硫酸铵复杂的分解反应可以通过计算动力学参数和反应机理来表示。同时，应结合多种反应机理来描述整个热分解过程。

2.2.1 无模型法的活化能（E）计算

将TGA 获得的实验数据用于研究热分解的动力学机制［17］。一般采用转化率变化来研究固体焙烧的动力学。固体转化率的计算方法见式（7）［18-19］：

式中：α为固体转化率，%；m0为初始质量，mg；mt为t时刻的质量，mg；me为残余质量，mg。

在其他条件相同的情况下，考察了硫酸铵在不同升温速率下的TG曲线，结果见图6。从图6看出，每一阶段的反应温度区间随着升温速率的增加向更高温度区间移动。以温度为自变量无法准确区别各个反应阶段的温度范围。由于从一个阶段到另一个阶段其质量损失率是相同的，当反应进行到一定程度时，反应的控制步骤就会发生变化，这与升温速率的变化无关。因此，将每个阶段作为自变量，将其分成10等份，具体数据见表2。

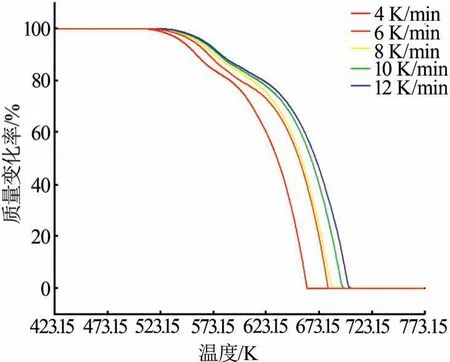
图6 不同升温速率下硫酸铵的TG曲线Fig.6 TG curves of ammonium sulfate at different heating rates

无模型方法在不确定模型函数的情况下计算动力学参数具有明显的优势［20］。在本研究中使用以下两种无模型方法计算活化能，即Ozawa-Flynn-Wall（OFW）和Kissinger-Akahira-Sunose（KAS）。在OFW方法中［21］，机理函数G（α）在不同升温速率条件下不随转化率（α）变化，见式（8）。在任意选定的α处，以lnβ为纵坐标，以1.051 6E/RT为横坐标，根据不同温度下对应的α数据进行拟合得到拟合直线，按照其斜率求不同转化率（α）相对应的活化能（E）。

式中：β为升温速率，K/min；A为指前因子，s-1；E为活化能，kJ/mol；α为转化率，%；R为摩尔气体常数，8.314 J/（mol·K）；T为热力学温度，K。

在KAS方法中［22］，机理函数G（α）在不同升温速率条件下不随转化率（α）变化，见式（9）。以ln(β/T2)为纵坐标，以1/RT为横坐标，根据不同温度下对应的α数据进行拟合得到拟合直线，按照其斜率求不同转化率（α）相对应的活化能（E）。

对于这3 个分解阶段，在不同转化率下每个阶段的活化能通过公式（8）和（9）计算。图7 为通过KAS 和OFW 方法计算硫酸铵分解过程的3 个阶段的活化能。从图7 看出，在同一阶段不同转化率下应用KAS 和OFW 方法计算的活化能参数趋势一致且接近，表明结果可靠。以计算的活化能为基础进行机理函数的选择。将图7中各阶段不同转化率下的活化能相加取平均值为该阶段的平均活化能：第一阶段KAS 方法的平均活化能为123.55 kJ/mol、OFW 方法的平均活化能为126.34 kJ/mol；第二阶段KAS 方法的平均活化能为100.25 kJ/mol、OFW 方法的平均活化能为104.36 kJ/mol；第三阶段KAS 方法的平均活化能为93.27 kJ/mol、OFW方法的平均活化能为99.05 kJ/mol。

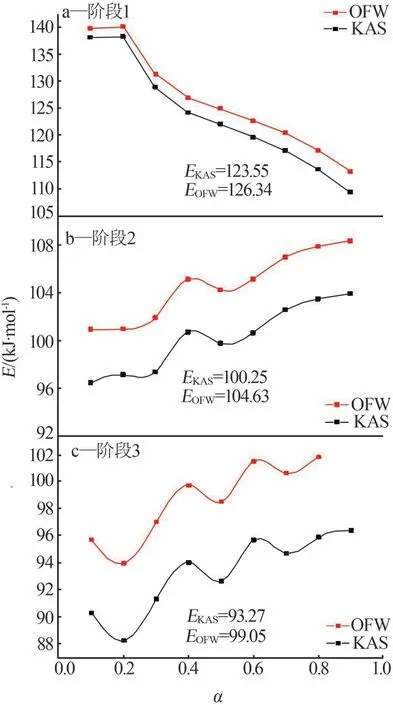
图7 OFW和KAS方法各阶段活化能（E）与转化率（α）的关系Fig.7 Activation energy（E）in relation to conversion(α) for each stage by OFW and KAS methods

2.2.2 模型拟合确定机理函数

为确认各阶段的机理函数，采用Coats-Redfern（CR）模型对实验数据进行拟合［23-24］，见式（10）。选择相关系数高且活化能接近OFW 法和KAS 法计算的活化能的机理函数。

将常规固相分解反应机理函数引入到CR 方法中［25］。通过绘制ln［G（α）/T2］与1/T的线性图，得到活化能（E）、相关系数（R2），计算结果见表3。

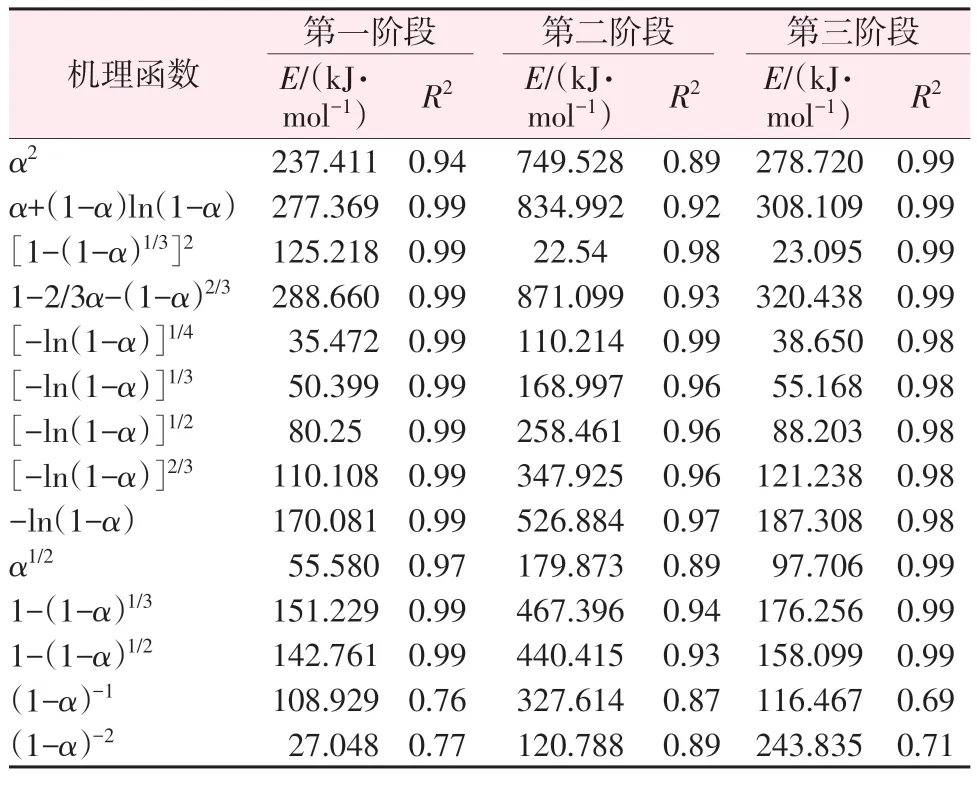
表3 Coats-Redfern法推断结果Table 3 Inference results by Coats-Redfern method

根据表3的推断结果对最概然机理函数拟合作图，结果见图8，动力学参数见表4。在反应的第一阶段，硫酸铵开始发生固体分解，进行脱氨反应形成硫酸氢铵和氨气。由于硫酸铵发生分解的温度高于硫酸氢铵的熔点温度，所以随着反应的进行硫酸铵晶体表面被熔融状态的硫酸氢铵所包覆。随着反应温度继续升高，形成硫酸氢铵的产量不断增多，硫酸铵的含量不断减少，热量传递到硫酸铵的过程会随着硫酸氢铵产量的增加而变得困难。温度越高，化学反应控制的因素变得越不明显。当到达第二阶段反应的温度时，液态硫酸氢铵开始发生脱水反应形成焦硫酸铵，液态硫酸氢铵的流动有助于焦硫酸铵晶体的形成。因此，硫酸铵分解第一阶段为三维扩散、球形对称、减速型α-t曲线；第二阶段为随机成核和随后增长机理，符合Avrami-Erofeev 方程。第一步分解最可能的机理函数是G（α）=［1-（1-α）1/3］2；第二步分解最可能的机理函数是G（α）=［-ln（1-α）］1/4。当温度进一步升高时，焦硫酸铵的化学键处于不稳定状态，焦硫酸铵会迅速分解。因此，在如此高的温度下，控制步骤不是焦硫酸铵的化学反应，而是气体产物的传热和扩散沉淀过程，遵循Mampel Power Law机理，机理函数为G（α）=α1/2。

表4 最概然机理函数和动力学参数Table 4 Most probable mechanism function and kinetic parameters

3 结论

主要利用TG、MS、XRD、FT-IR检测技术对硫酸铵分解行为进行研究，确定硫酸铵分解可以分为3个阶段。每个阶段的分解机理分别是（NH4）2SO4=NH4HSO4+NH3（g）、2NH4HSO4=（NH4）2S2O7+H2O（g）、3（NH4）2S2O7=2NH3+2N2+6SO2+9H2O。利用Coats-Redfern 法计算出硫酸铵分解3 个阶段的平均活化能分别为125.218、110.214、97.706 2 kJ/mol，最概然机理函数分别为Jander 方程（n=2）、Avrami-Erofeev方程（n=1/4）、Mampel Power Law方程（n=1/2）。通过此研究可以为硫酸铵的充分利用提供理论基础。