基于BP神经网络的基坑开挖对临近桥桩水平位移预测研究

田佳学

(中铁十七局集团第三工程有限公司 河北 石家庄 050000)

0 引言

基坑开挖会造成周边土体位移,从而对其影响范围内的桩基施加附加应力,导致桩基侧移或承载力不足,对桩基产生不利影响,若不采取有效控制,长久以往,势必会造成桩基上部高建(构)筑物不均匀沉降,引发桩基下部土局部破坏,甚至会使桩基产生扭曲形变,严重危害建(构)筑物的使用安全。

现阶段对桩基位移的研究方法主要有理论解析解法、现场实验法、有限元分析法,由于基坑开挖对邻近桩基侧移影响较大,例如:基坑开挖体积、开挖次序、基坑支护综合刚度、水文地质条件、桩基直径、桩基与基坑间距等都会对邻近桩基产生影响,而且无法用线性关系准确描述桩基变形,所以采用上述分析方法求解桩基侧向位移均较为烦琐且耗时较长。如果利用人工智能算法的模糊性、非线性、泛化能力等特点对已有实际基坑工程案例进行计算分析[1-2],并与现有分析方法结合,将会对桩基稳定性的判别有所帮助。

人工神经网络是热门的交叉学科,在信号处理、图像识别、经济预测、机器人控制等工程领域应用广泛[3]。在岩土工程领域,孙钧院士等[4]于2000年以润扬长江公路大桥为背景,建立多步滚动神经网络模型,通过对墙体位移进行动态预测,当预测值即将达到最大规定阈值时,不必采用注浆等传统地基加固方法,可以通过优化基坑施工参数规避变形。袁金荣等[5]通过对基坑墙体位移的动态预测,认为神经网络技术在地下工程应用中会有很好的适用性。卢礼顺等[6]基于上海某地铁车站基坑,利用BP神经网络建立基坑与相邻桩基之间的预测模型,通过输入桩基的变形值,预测了开挖过程中基坑的允许变形值。赵华菁等[7]利用神经网络和深度网络预测地下连续墙的变形值,并依据交叉验证法验证了预测模型的稳定性,结果证明,历史变形数据数量越多,预测模型的稳定性越高,误差也会相应减小。

本文对50个邻近基坑的桩基实际工程案例进行统计,考虑基坑尺寸、支护体系总体刚度、桩基与基坑距离等因素,将实际数据与人工神经网络相结合,通过建立BP神经网络预测模型,预测桩基水平位移,对实际工程桩基稳定性预测提供一定帮助。

1 人工神经网络预测

1.1 BP神经网络简介

人工神经网络算法的目的是找到对函数损失影响程度最小的参数,其主要由网络架构、激活函数、找出最优权重值的参数学习算法3部分构成。反向传播(Back Propagation)算法[8]是一种按照误差逆向传播算法训练的多层前馈神经网络,于1974年由Werbos提出,1986年,Rumelhart和MeCelland等[9]科学家发展了此理论,作为目前应用最广泛的神经网络算法之一[10],极大地推动了神经网络算法的二次发展。

1.2 BP神经网络原理

BP神经网络算法主要由输入层、隐含层、输出层3部分构成[11],其学习过程由信号的正向传播与误差的反向传播两个过程组成。

正向传播过程中,数据从输入层到隐含层最后到输出层,中间均需要经过权重值和偏置项的线性变换处理,若输出的实际结果与期望结果不符,则开始反向传播过程;若二者结果相符,则结束运算。反向传播时,将结果误差按原通路返回计算,反传过程中将误差分摊给所有单元,获得每个单元的误差信号,将该信号作为修正单元权值的依据。

BP神经网络的本质为使用梯度下降来搜索可能的权向量的假设空间,以找到最佳的拟合样例的权向量。具体而言,即利用损失函数,每次向损失函数负梯度方向移动,直到损失函数取得最小值。

假设输入层数据为x,隐含层输出向量为y,输出层向量为o,期望输出值d,输入层到隐含层之间的权值为w,隐含层到输出层之间的权值为v,激活函数为g,结果误差为E。

对于输入层到隐含层

(1)

对于隐含层到输出层

(2)

结果误差为

(3)

将式1、2分别带入式3,即可得出隐含层误差为

(4)

输入层误差为

(5)

式5为损失误差函数,该函数由权值v、w表示,赋予v、w恰当的值时,误差可达最小,不同的权值初始值会影响神经网络收敛极小值[12],只要按着梯度下降的方式更新权值即可找到恰当的权值。

隐含层的权值调整量为

(6)

输出层的权值调整量为

(7)

(8)

(9)

将式8、9带入式6、7最终可得隐含层和输出层的公式为

(10)

Δvjk=η(dk-ok)ok(1-ok)yj

(11)

2 基于BP神经网络的预测模型

2.1 模型训练样本选取

根据BP神经网络的特性,需要选取一定数量的具有代表性、针对性的训练样本,将样本作为输入条件,考虑到输出结果的准确性和模型计算的速度,样本数量不能过多或过少[13]。

本文研究基坑开挖对邻近桩基的影响,选取了基坑开挖尺寸、基坑与桩基间距、基坑围护结构总体刚度、桩基直径、地质条件5个主要因素作为输入变量。对桩基影响程度小或者难以取得的其他因素,不作为输入条件。

2.2 预测模型的构建

如图1为BP神经网络预测流程图,P为样本总个数,p为第i个样本,q为训练迭代次数,ERME为实际误差,EMIN为误差阈值。具体流程为:(1)赋予初始权值、阈值,二者初始值不能相等。(2)将所需要训练样本输入。(3)计算各层的输出误差并归一化处理。(4)对全部样本进行逐一计算,计算期望输出和实际输出之间的误差,并反向对权值和阈值进行修正。(5)当实际误差小于误差阈值时,结果满足精度要求,若不满足精度要求时,则返回流程(2)。

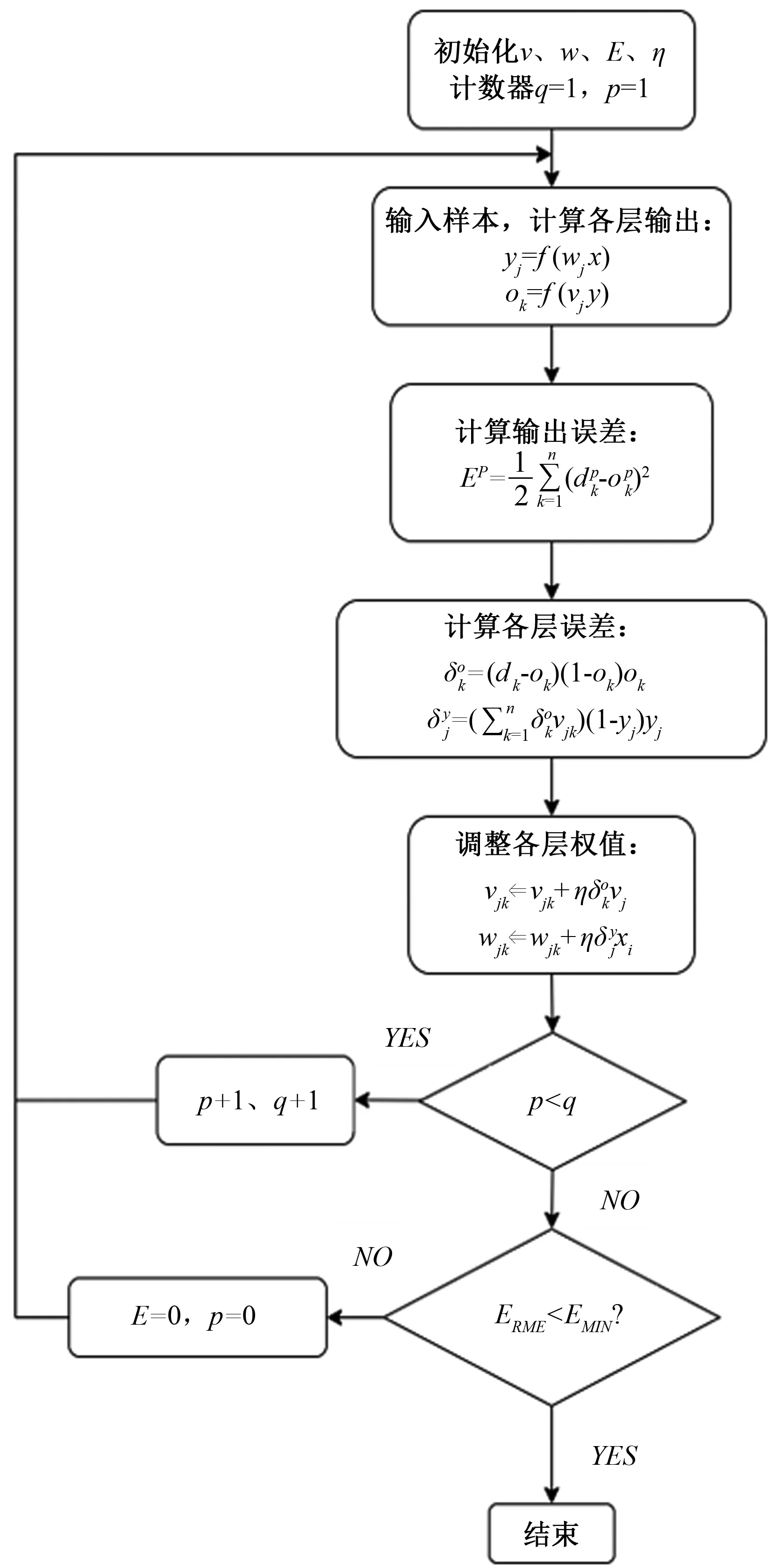
图1 模型预测流程图

3 基坑及临近桥梁工程概况及有限元模型建立

3.1 新建桥梁与邻近桥梁的位置关系

郑州大四环及大河路快速化工程是郑州市交通网“两纵两横两环”中的重要一环,潮河桥段工程连接南四环与大河快速路,新建桥梁为南北走向、双向八车道,设计宽度为24 m,该桥段由左右两侧各4组共8组桥墩支撑,选取中间一组进行分析,桥段两侧为既有桥梁,与两侧邻近桥梁的夹角为30°,二者位置剖面图如图2(a)。新建桥梁两侧分别有4根桥桩,桩间距为6.235 m,桩直径为1.5 m,桩承台宽度为1.7 m,高度为1.5 m,长度为23.383 m。如图2(b)所示,新建桥墩距左边桥面距离过近,右边桥面距离桥墩40 cm,左边桥面距离桥墩仅5 cm。

图2 新建桥梁示意图

3.2 基坑概况

新建基坑位于水流平缓的潮河中,处于邻近桥梁正中央的位置,整体呈狭长矩形,长度为35 m、宽度为11.9 m,开挖深度为6.6 m。采用拉森式钢板桩支护作为止水帷幕,嵌固深度为15 m,高出水面0.5 m,河床面以下部分14.1 m,同时采用400 mm×400 mm钢围檩与Ф800 mm×16 mm钢支撑相结合的方式作为围护结构,基坑剖面图如图3所示。

图3 基坑剖面图(单位:mm)

基坑施工场地范围内的地层从上至下共分为4层地质,依次为淤泥质土、粉砂、粉土、细砂。表1为地质工程勘察结果所提供的土层的物理力学参数。

表1 土层物理力学参数

3.3 施工监测

为了确保基坑施工过程中基坑围护结构的稳定性以及两侧潮河桥梁的安全性,如图4所示,通过在基坑内部布置变形监测设备动态化监测基底垂直位移、钢板桩水平与垂直位移、潮河桥护栏水平与垂直位移,监测过程中要保证持续监测。若发现风险问题,需要制定方案及时做出调整。

图4 基坑监测布点图

3.4 模型简化及条件假定

为了方便模型计算,对建模过程中条件进行优化及假设:(1)模型采用勘察单位提供的地层参数来描述土体的泊松比、重度等物理力学性质,假设土体、桩基和承台等为各向同性且均质的理想弹塑性体;(2)忽略河水对基坑开挖过程的影响;(3)基坑围护结构视为各向同性的均质线弹性结构;(4)采用生死单元来模拟基坑开挖阶段,忽略时间效应的影响。采用ABAQUS软件建立三维有限元模型,对基坑开挖及围护结构施作等过程进行模拟。

3.5 基坑开挖三维模型

为研究基坑开挖引起的临近桥桩的变形情况,以新建桥梁为例进行数值建模,新建桥梁基坑开挖段两侧各有4组桥桩已施工完毕。图6为模型网格划分图,为了减小边界效应对计算结果的影响,分别取模型X、Y、Z方向为120 m、100 m、80 m[14]。单元总数共321306个,节点总数共250600个,实体单元网格采用C3D8R单元类型,内支撑采用梁单元进行模拟,钢板桩以壳单元进行模拟,将图5中的桥梁桩基所承受桥面荷载以施压荷载的方式施加于桩基承台。

图5 网格模型划分图

图6 桥桩竖向变形放大图

4 桥梁整体变形

4.1 桥梁变形趋势

图6为放大后的基坑开挖引起的临近桥梁竖向变形图,桥梁整体呈上拱型,随着距基坑距离的增大,桩基变形值逐渐减小,变形值基本一致。如图7,以右侧桥梁为例,桥梁竖向位移在开挖过程中均大于水平和纵向位移,靠近于基坑一侧桥端为端头,另一端为端尾,端头变形大于桥梁端尾,端头变形最大值为3.19 mm,端尾变形最大值为0.32 mm。根据监测数据可知,桥端3个开挖阶段竖向位移分别为0.34 mm、0.89 mm和3.31 mm。通过对比分析可知,有限元计算结果比较保守,与监测结果基本一致。

图7 右桥梁变形图

4.2 桥桩水平位移

如图8所示,左右桥桩的水平位移基本一致,靠近于基坑的桥桩变形最大(左一、右一桥桩),最大变形位于基坑开挖面以上2.25 m处,左右两端变形值基本一致,变形值分别为1.08 mm、1.1 mm,左右两侧桥梁沿水平方向变形相反,均背离基坑中心。由于桥面约束作用,右二桥桩在基坑上部位置变形方向与右一相反,右二桥桩最大变形位置位于桥桩24 m处,最大变形值为0.75 mm。右三桥桩端部变形值与桥桩30 m处变形值基本一致,右四桥桩最大变形值为0.67 mm,位于桩端,最小值仅为0.01 mm,右三与右四最小变形均位于桥桩16 m处附近,可见随着桥桩与基坑间距的增大,基坑开挖对桥桩的影响可忽略不计。

图8 桥桩水平位移图

5 BP神经网络预测及结果分析

5.1 神经网络训练测试

利用MATLAB软件,将收集的50组数据作为训练样本输入(部分输入变量如表2所示),进行预测结果的回归性分析,本文设置一个输出层节点即桩基水平位移,通过图9的训练结果可见,BP神经网络的训练预测结果较好,预测输出与期望输出结果误差较小,测试样本基本分布于理想曲线附近。

表2 部分样本数据

图9 BP神经网络拟合图

神经网络的训练学习的实际值和预测值如图10所示,经过15次迭代,实际值和预测值重合度较高,达到了指定的目标误差。由于本次训练样本较少,增加样本数量可以进一步提高训练预测精度。

图10 训练的预测值和实际值

5.2 预测结果分析

本次预测模型运算学习速率0.01、目标误差性能0.9、动量误差分别设置为10-4[14-15],同时将训练样本作为测试样本,计算BP神经网络的预测误差。由图11可知,除右四桥桩预测结果不可取之外,其余桥桩最大水平位移预测结果均较为准确,可以看出神经网络训练拟合程度很高,实践证明,若增加训练样本数量,可进一步提高预测精度。

图11 桥桩水平预测图

6 结论

以郑州大四环及大河路快速化工程为背景,运用数值模拟与监测数据对比的研究方法对基坑开挖对临近桥桩的影响进行分析。同时结合BP人工神经网络对相似工程桩基最大水平位移进行训练,之后对该工程桥桩最大水平位移进行预测,并与实测数据对比验证,得出以下结论:

(1)基坑开挖对邻近桥梁桩基的影响会随着桥梁桩基与基坑边缘的距离的增大而慢慢减弱,对桥梁桩基的影响主要体现在基坑开挖卸荷过程中土体回弹造成的桩基竖向位移,且桥梁产生的竖向位移在开挖过程中始终大于其他方向位移。

(2)本文构建的BP神经网络模型对该工程桥桩最大水平位移的预测与实际值吻合度较高,在实际应用中可以利用该预测模型判断基坑开挖时临近桥梁桩基的稳定性,对其他相似工程具有参考意义。

(3)在神经网络模型预测中,收集更多的输入样本会提高模型的稳定性,提高预测精度,但考虑过多的非重要影响因素会降低模型预测的准确度。对样本的各种因素进行合理量化,提高关键因素权重,适当约简非关键因素来训练预测模型,可以提高预测的准确性。