耦合回音壁模式微腔系统中高阶边带的产生与调控

贾 晓,韩志杰,汪 宝,王运锋

(南阳理工学院信息工程学院 河南 南阳 473004)

0 引言

光学微腔是通过循环谐振作用将光限制在小体积内并且能够长时间维持的光学器件[1]。光学微腔的尺寸小至微米、纳米量级,可以显著提升腔内的光功率,增强光与介质间的相互作用,因此,光学微腔在基础物理研究中被广泛应用。回音壁模式光学微腔是一种典型的光学微腔,这种光学微腔在制作时使用了吸收率较低的介电材料和更为精密的加工技术,使得微腔内部的腔壁光滑度较高且传播损耗较小。基于以上两点,回音壁模式光学微腔有更小的模式体积、超高的Q值(目前,实验室观测到的最高品质因子可达1010量级[2])和极窄的线宽。此外,回音壁光学微腔还易于加工、集成与封装,因此相比法布里-珀罗腔、光子晶体缺陷腔,回音壁模式光学微腔有着更广阔的应用前景。自高品质因子的回音壁模式微腔受科学界关注以来,回音壁模式光学微腔结构也由最简单的圆柱形和微球形结构发展到微盘、微环、光子晶体腔等,甚至包括瓶口结构和微泡结构[3]。迄今为止,回音壁模式微腔的研究成果已在包括非线性光学、光学传感以及大容量相干光通信等领域得到了广泛应用[4]。

非线性光学主要研究强光和非线性材料间的非线性效应。克尔非线性效应是一种三阶非线性效应,是非线性光学研究的重点之一。高阶边带是指一系列离散的、等频率间隔的光谱,是驱动光经过参量转换产生的[5]。在较强激光场的作用下,克尔非线性会导致输出光中出现二阶、三阶甚至更高阶边带的频谱成分,这个现象与光与原子相互作用的非线性导致多个光子的产生与吸收从而出现高次谐波的现象在本质上是一致的[6]。高阶边带是一类重要的非线性效应,可以作为频域的“光尺”来精确测量光的频率[5],因此获得数量更多的边带是促进其应用于精密测量的一个重要因素。

1 物理模型与动力学方程

耦合回音壁模式微腔系统示意图如图1所示,系统由两个回音壁模式的微腔组成。图1上、下方的回音壁模式微腔分别为腔1和腔2。系统由双色激光场驱动,包括控制光和探测光,其中控制光的角频率、强度、功率分别为ωc、Sc、Pc,探测光的角频率、强度、功率分别为ωP、SP、PP。双色驱动光经锥形光纤耦合进入腔中,驱动腔的谐振模式a1,该入射光从锥形光纤的左侧与腔模a1耦合,经过下方锥形光纤耦合并从光纤右侧输出的模式为腔模a1的顺时针(clockwise,CW)模式。同理,该驱动光从锥形光纤的右侧与腔模a1耦合,经下方锥形光纤耦合并从光纤左侧输出的模式为腔模a1的逆时针(counterclockwise,CCW)模式。腔1和腔2中的顺时针模式和逆时针模式的本征频率都为ω0。

在驱动场作用下,系统的哈密顿量在频率为ωc的旋转框架下可表示为

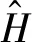
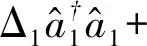
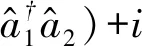
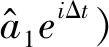
(1)

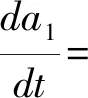
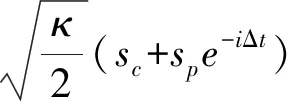
(2)

(3)

2 结果与讨论

利用龙格-库塔法数值求解非线性常微分方程(2)和(3),设定初始条件为:a1|t=0=0,a2|t=0=0。数值计算使用的系统参数[7]为κ/π=10 MHz,U=80,Δ1=Δ2=Δ=κ,J/π=23.4 MHz,Pc=0.32 mW。首先,取控制场和探测场的功率都为Pc=Pp=1.3 mW,在这种情况下,探测场的强度与控制场强度相同,处于非微扰机制,图2(a)表示在此功率的双色激光场驱动下,腔1内的光子数|a1|2随时间的演化情况。从图2(a)中可以看出,在经历了约0.2 μs的弛豫过程后,光子数随时间的演化呈现稳定的周期性变化,与正弦振荡类似,频率为5 MHz,平均光子数|a1|2≈2×106。再提高驱动功率至Pc=Pp=3.5 mW,腔1内的光子数随时间的演化情况如图2(b),振荡的弛豫时间和频率不变,仍为0.2 μs和5 MHz,而平均光子数增加到约3×106。

图2 腔场光子数|a1|2在不同的驱动功率下随时间的变化

图3 驱动功率为1.3 mW时系统的输出高阶边带频谱图

图4 驱动功率为3.5 mW时系统的输出高阶边带频谱图

光学高阶边带产生的物理机制是参量频率转换,包括非线性简并和非简并四波混频过程,是由三阶克尔非线性产生的。图5清楚地描述了通过四波混频产生高阶边带的基本原理[8,9]。双色驱动场的能量通过两个过程传递到边带:第一步,频率为ωc的两个相同的光子和频率为ωp的光子通过简并四波混频转换为频率为ω-1的新的下转换光子。第二步,实际边带的产生是非简并四波混频的结果,具体过程为3个频率分别为ωn-1,ωn和ωn+1的光子转换为频率为ωn-2(ωn+ωn-1→ωn+1+ωn-2)或ωn+2(ωn+ωn+1→ωn-1+ωn+2)的新光子。连续的四波混频过程会产生一系列等间距的频率成分,即高阶边带,相邻的两个边带之间的间距是控制光和探测光的差频Δ=ωp-ωc,每个边带表示的光频率为ωn=ωc+nΔ,其中整数n表示边带的阶数。

3 结论

本文研究了耦合回音壁模式微腔系统中高阶边带现象的产生与调控,并分析其背后的物理机制。首先利用龙格-库塔法数值求解系统的非线性动力学演化方程得到腔场光子数随时间的变化情况,然后对输出光场做快速傅里叶变换得到系统的输出频谱。发现当驱动功率为1.3 mW时,高阶边带最多为33阶,当提高驱动功率至3.5 mW时,高阶边带最多为50阶。高阶边带产生的物理机制是四波混频,包括简并和非简并四波混频。本文的研究结果为低功耗芯片型光频梳器件的研发提供了一定的理论基础。