改进思维进化算法优化BP神经网络的瓦斯涌出量预测研究

赵焕平

(南阳理工学院计算机与软件学院 河南 南阳 473004)

随着煤矿开采强度和深度的增加,瓦斯涌出问题愈加严重,对瓦斯涌出量精准预测是保障煤矿安全生产,矿井工人生命安全的有力措施之一。近年来,国内外学者对瓦斯涌出量预测进行了大量研究,如支持向量机[1]、回归分析法[2]、混沌时间序列、灰色理论[3]及神经网络[4-7]等。这些方法各有各的特点,也取得了一定的成果,但是这些方法的预测误差比较大,存在一定的局限性。由于瓦斯涌出量受到多种因素的影响,因而BP神经网络在瓦斯预测研究中应用广泛,但其存在收敛性差及容易陷入局部最优的不足。本文借助于改进的思维进化算法优化BP神经网络初始权值和阈值,在思维进化算法中引入精英反向学习策略优化种群的多样性,将粒子群算法应用于MEA的趋同操作提升收敛速度,避免陷入局部最优。

1 相关理论

1.1 思维进化算法(MEA)

思维进化算法[8]是在遗传算法的基础上衍生出的新型进化算法,它继承了遗传算法的“群体”和“进化”思维模式,同时又提出了“趋同”和“异化”操作模式。思维进化算法随机产生一定数量的个体,根据每个个体的适应度值分为优胜个体和临时个体,分别以这些个体为中心,在其周围产生若干个体,形成优胜子群体和临时子群体。在子群体内部,通过趋同操作使各群体朝着局部最优的方向进化。而异化操作是在整个解空间中,各个子群体进行全局竞争来保证群体的全局搜索能力,使种群朝着全局最优发展,趋同和异化在进化过程不断迭代,直到找到最优解。

1.2 改进的MEA算法

为了克服MEA算法任意初始化种群和子种群的弊端,增加种群的多样性,使个体能够尽可能地实现均匀分布,将精英反向学习策略[9](OBL)和粒子群算法[10-11](PSO)应用于思维进化算法中的趋同操作中,提高子群体内局部最优解的质量,增加算法的全局搜索能力。

种群中子群体移动速度的公式为

Vi={vik|vik→F(xik)=opt.(F(xij))}

(1)

式中vik表示子群体中个体的迁移速度,F是评价函数,xik是子群体Gi中第k个个体。

子群体的位置转移公式为

Vi(t+1)=wVi(t)+c1r1(bsti(t)-Hi(t))+c2r2τi(t)(hbst(t)-Hi(t))

(2)

Hi(t+1)=Hi(t)+Vi(t+1)

(3)

τi(t+1)=pi·τi(t)

(4)

式中Hi(t)是子群体Gi在t时刻的行为,pi是Gi在t时刻的信息强烈程度,信息衰减因子τi是历史最优解对Gi的影响程度,bsti(t)是Gi在t时刻的历史最优位置,hbst(t)是整个群体在t时刻的历史最优位置。

为突出群体的自身最优和全局最优,将其定义为精英子群体,则其反向解为

也可表示为

(5)

式中

daj=min(xi,j),dbj=max(xi,j) ,daj和dbj为第j维搜索空间的动态边界。

为了保存搜索经验,用动态边界代替固定边界,引导反向解进入缩小的搜索空间。此外,为了避免反向解跳出边界成为非可行解,采用随机生成的方法对其进行重置,如式(6)所示

(6)

2 基于MEN-OBL-PSO的BP神经网络

算法的具体寻优步骤(如图1)为:

图1 算法模型结构

步骤1:产生初始种群。

步骤1.1:按照反向学习策略在整个解空间生成S个个体。

步骤1.2:对每个个体进行优劣评价,选择得分最高的M-T个个体作为优秀个体。

步骤1.3:以每一个优秀个体为中心,服从正态分布产生N个个体,构成M-T个优秀子群体,T个临时子群体。

步骤2:趋同操作。在每一子群体内,根据加入精英反向学习策略和粒子群算法对每一个体进行得分计算,得分最高的个体为优胜者,利用公式(1)至(6)以优胜个体为中心生成新的子群体,重复进行搜索过程直到得分最高的个体不再发生改变,该子群体成熟,子群体的得分即为在算法搜索过程得分最高的个体得分。

步骤3:异化操作。若当前优胜子群体的得分低于临时子群体得分,则用此临时子群体替换当前的优胜子群体,并释放当前含有N个个体的优胜子群体,重复优胜群体和临时子群体的对比,筛选出群体最优解。

步骤4 :重新生成临时子群体。

步骤5:收敛条件的判断。当算法满足终止条件:全局公告板优胜者的得分不再发生改变,思维进化算法优化结束,从而得到全局最优个体;否则返回步骤2。

步骤6:将最优个体通过解码得到BP神经网络最优权值和阈值。

步骤7:训练BP神经网络。

3 实验结果及分析

3.1 数据来源

由于我国矿井地质情况复杂,影响瓦斯涌出量的因素众多,综合考虑数据,主要影响因素有:开采煤层瓦斯含量x1、煤层埋藏深度x2、煤层厚度x3、煤层倾角x4、工作面长度x5、日推进速度x6、煤炭采出率x7、邻近层瓦斯含量x8、层间距x9、层间岩性x10、开采强度x11。其中层间岩性x10属于定性指标,无法直接测得,作为输入数据前需进行量化处理。

考虑到数据的广泛性,把全部数据按式(7)先进行归一化处理。

(7)

层间岩性的量化值由围岩硬度加权平均值替代

(8)

式中,n是围岩层数,H为开采层和临近层围岩总厚度,fm是第m层岩层硬度,hm是第m层岩层厚度。

选取某矿业集团连续18个月的回采工作面瓦斯监测数据,回采工作面瓦斯涌出量Y与影响因素数据如表1所示。

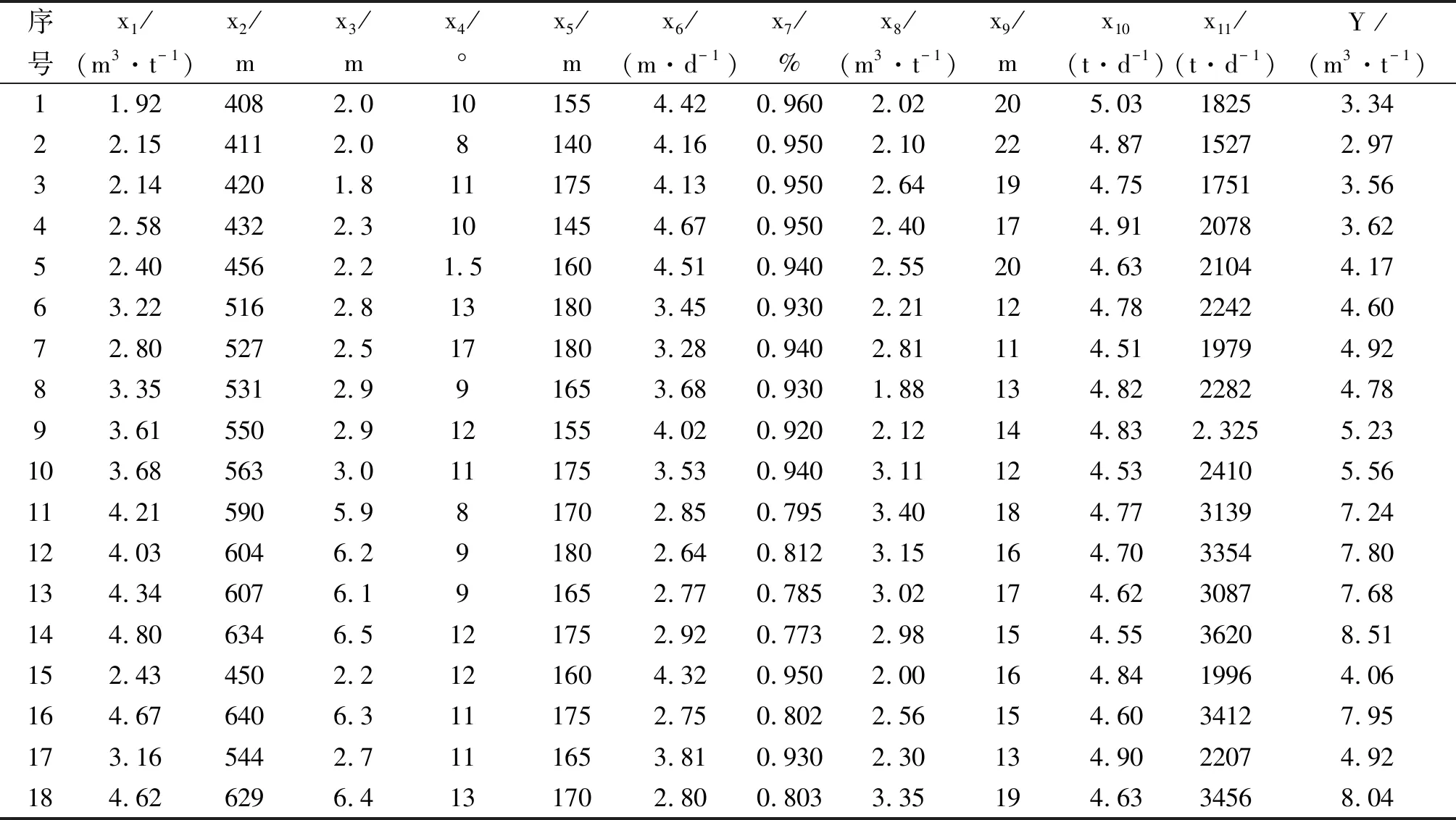
表1 回采工作瓦斯涌出量与影响因素数据

3.2 预测仿真结果分析

根据选取的BP参数,对3种模型进行网络训练,误差训练曲线如图2所示。

图2 不同神经网络误差训练曲线

BP神经网络模型需要2348步达到一定的收敛精度,MEA-BP神经网络模型则需要1562步达到一定的收敛精度,而MEA-PSO-OML-BP模型在623步就达到收敛精度,由此可见,MEA-PSO-OML-BP神经网络具有更快的收敛速度。

保存训练好的BP神经网络,根据模型的预测步骤,采用Matlab软件结合样本数据对瓦斯涌出量进行仿真试验,不同模型得到的仿真输出如图3所示。表1中前12组作为训练样本,后6组用来检验模型的精确程度。由图3可知MEA-OBL-PSO-BP模型能很好地逼近实际值,具有较高的精度。

图3 不同模型预测仿真结果与实测值对比

为了更好地对本文提出的模型进行评价,用均方根误差(RMSE)和平均相对误差(MRE)来衡量模型的预测精确程度,用平均相对变动值(ARV)来衡量模型的泛化能力。

(9)

(10)

(11)

通过对BP神经网络,MEA-BP神经网络和本文预测模型运用实验数据进行预测仿真,得到结果如表2所示。

表2 不同模型的预测结果对比

由表2可知,BP神经网络的平均相对误差为8.26%,MEA-BP神经网络的平均相对误差为3.33%,说明MEA-BP神经网络具有更高的预测精度,这是由于MEA-BP神经网络利用思维进化散发自动寻优优化了BP神经网络的关键参数-权值和阈值。MEA-OBL-PSO-BP神经网络的平均相对误差为0.81%,相对于BP神经网络和MEA-BP神经网络的预测结果是最好的,说明该模型预测结果更接近于实测数据,这是由于精英反向学习策略和粒子群算法保证了种群的多样性,避免算法陷入局部最优。不同神经网络模型相对误差曲线如图4。

图4 不同模型预测结果相对误差对比

由图4可知,BP神经网络预测结果误差最大,随机波动性较大,MEA-BP神经网络预测误差次之,MEA-OBL-PSO-BP神经网络预测误差最小,且误差波动比较平缓。由表2可知,本模型的ARV值为0.00116,明显小于其他两种模型,说明该模型具有很好的泛化能力。由此可见MEA-OBL-PSO-BP具有较高的预测精度和较好的泛化能力,能够准确地对矿井瓦斯涌出量进行预测,达到理想的预测效果。

4 结语

瓦斯涌出量的精准预测是矿井进行提前预警的重要参考信息,而瓦斯预测因子信息是高度非线性的,BP神经网络虽然具有很强的非线性处理能力,但收敛慢且容易陷入局部最优。将MEA与BP神经网络结合起来,用精英反向学习策略和粒子群算法的思想优化思维进化算法,以获取最优的BP神经网络的权值和阈值。实验结果表明,该模型具有更高的预测精度和泛化能力,且预测相对误差为0.81%,明显优于常用的BP神经网络和MEA-BP神经网络,对于今后瓦斯涌出量的预测具有一定的参考价值。