我国中学数学建模领域研究热点、演化路径与未来趋势——基于CiteSpace的知识图谱分析

周长峰,郭顺利

(1.临沂市费县实验中学,山东临沂,276299;2.曲阜师范大学传媒学院,山东日照,276826)

一、引言

数学是人类对事物的抽象结构与模式进行严格描述和推导的一种通用手段,在工程技术、自然科学、计算机科学等领域发挥着举足轻重的作用,是当代技术发展乃至人类生活的重要基础学科。数学建模通过建立数学模型对实际问题的本质属性进行抽象刻画,再运用合理的方式对模型参数进行求解,从而达到解决问题的目的。数学建模是数学的重要分支之一,也是连接实际问题与数学知识的桥梁。对初中阶段的学生而言,他们已经具备一定的数学知识和问题理解能力,教师在此基础上培养他们的数学建模思维与能力,可促进他们对数学知识的灵活运用,充分调动他们的学习兴趣,并有利于他们创新意识与创造能力的培养及实践能力的提高。我国十分重视对中学生数学建模能力的培养,《普通高中数学课程标准(2017年版)》将数学建模列为数学学科核心素养之一。

中学数学建模的研究备受我国教育学者的关注,已有学者对这一领域的研究成果进行了梳理和分析。比如,牛伟强等人使用内容分析法对1989—2016年发表的中小学数学建模文献进行了系统分析,指出了中小学数学建模存在的问题,并给出了具体的建议。[1]张勇强等人采用内容分析法从年代分布、作者来源、研究方法、研究关注的对象、内容领域和研究议题等维度,对2001—2021年我国核心期刊及其他数学教育主流期刊刊发的中小学数学建模文献进行了系统梳理,并给出了发展展望。[2]孙凯使用案例分析和内容分析的方法对跨度二十年的中学数学建模研究进行了回顾,发现研究成果主要集中在数学建模教学、内涵、评价等方面,同时指出了中学数学建模研究的不足之处,并对未来研究进行了展望。[3]但目前国内学者多使用质性分析方法总结中学数学建模研究现状,运用科学计量工具进行可视化分析的较少。基于知识图谱的量化研究可清晰客观地反映某一研究领域的研究热点、演化路径与未来趋势等内容,对研究的未来发展具有重要意义。

鉴于此,本研究以中国知网刊发的中学数学建模研究文献为数据样本,借助科学计量软件CiteSpace对我国中学数学建模领域的研究热点、演化路径与未来趋势进行探讨,为我国未来中学数学建模研究发展提供建议。

二、研究设计

(一)研究工具与思路

本研究主要采用文献计量法和知识图谱可视化的方法,对我国中学数学建模的相关文献进行分析。本研究对高频关键词进行了统计分析,对关键词聚类图谱进行了解读,对该领域的研究热点进行了分析,以揭示研究的演化路径,还对关键词突现情况进行了分析,以发现该领域研究的未来趋势。

(二)数据来源

本研究的数据来源于中国知网数据库,为精确查找到中学数学建模领域的相关文献,研究者分别以“中学数学建模”“初中数学建模”“高中数学建模”为主要主题检索词进行主题检索和关键词检索。在检索到的文献中选择“学术期刊”进行精炼,检索时间为2023年5月15日。经过人工阅读和筛选后,将数据导入CiteSpace软件进行格式转化与重复项过滤,最终得到我国中学数学建模研究领域1991年1月1日至2023年5月15日发表的669篇文献数据。

三、热点分析

文章关键词是对文章研究内容的高度凝练,对文章关键词进行相关分析可从中探寻领域内的研究热点。本研究通过关键词共现对领域内的关键词频次进行统计,在此基础上进行关键词聚类操作,进而总结出研究热点主题。

(一)关键词频次统计分析

结合CiteSpace软件生成的关键词共现图谱,并运用Excel对高频关键词进行统计,结果如表1所示。

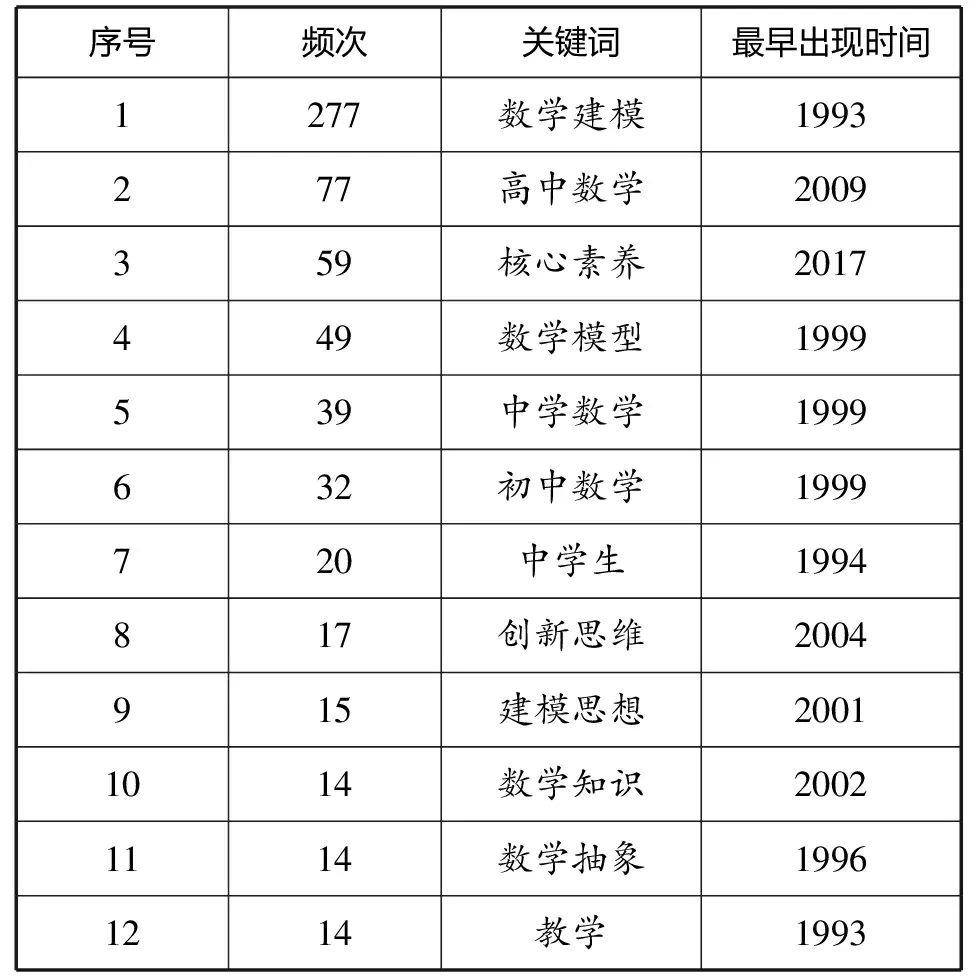
表1 高频关键词统计

由表1可知,关键词“数学建模”的出现频次最高,居第一位且远超其他关键词。值得关注的是,它的最早出现时间在20世纪90年代,说明相关研究者对该领域的研究关注时间较早,对数学建模进行了长期探索和深入研究。此外,关键词“高中数学”“初中数学”“中学数学”的出现频次也较高,说明数学建模在中学阶段的教育教学工作广受研究者关注。其中,“高中数学”的出现频次是“初中数学”出现频次的两倍多,意味着中学数学建模研究更倾向于高中阶段。这与学生心理发展特点及知识储备积累密切相关。关键词“核心素养”的出现频次较高且首次出现在2017年,这可能与《普通高中数学课程标准(2017年版)》的出台有关。数学课程标准首次提出了体现学科育人价值的学科核心素养,数学建模作为数学学科的六大核心素养之一广受关注。其他高频关键词如“创新思维”“建模思想”“数学知识”“数学抽象”也备受关注。

(二)关键词聚类图谱分析

在统计分析高频关键词的基础上,为进一步探寻关键词之间的共性,总结出研究热点主题,本研究对关键词进行聚类操作,得到如图1所示的关键词聚类图谱。

图1 关键词聚类图谱

#0数学建模是最大的聚类主题。该主题主要围绕关键词“数学建模”“应用意识”“应用能力”等展开。该聚类的研究主要聚焦中学数学建模教学和数学建模对数学知识应用的影响。例如,张莉结合高中数学建模案例对现代信息技术助力高中数学建模教学活动的开展进行了探究,提出了数学建模教学中值得思考的问题。[4]刘国庆等人在已有研究的基础上分析探讨了高中数学建模的教学策略,指出样例教学和变式练习是帮助学生提高数学建模能力的有效策略。[5]吴金凤认为数学建模思想对中学生数学应用能力的培养尤为重要,由此探讨了数学建模思想对数学教学的相关启示。[6]

#1核心素养是第二大聚类主题。该聚类的研究主要是将数学建模放在数学学科核心素养中探究,将数学建模作为培养学生数学学科核心素养的重要方面。例如,李院德等人探究了核心素养背景下高中数学文化教育的实施策略,认为充分发挥数学建模与数学探究活动的育人功能是高中数学教育落实数学文化的重要方面。[7]李洪忠基于数学核心素养对项目式学习进行了探究,将数学建模指导作为重要的项目式策略之一。[8]

#2数学抽象是第三大聚类主题。数学抽象是数学学科核心素养之一,它与数学建模相生相长:在数学建模中抽象函数模型,在数学抽象中积累数学建模中数据分析的经验。[9]该聚类的研究聚焦学生学科核心素养的培养,及数学抽象与数学建模的教学实施。例如,武海娟等人认为一元一次方程是初中数学教学的重难点,其教学应该着眼中学生数学抽象思维及数学建模能力和意识的培养。[10]

#3中学数学是第四大聚类主题。该聚类的研究主要探讨中学数学教学中的数学建模教育,包括课程的开发、教学的策略等方面,多以中学为研究的应用领域。例如,徐稼红对开设中学数学建模课程的意义、基本内容等进行了分析阐述。[11]

#4建模是第五大聚类主题。该聚类的高频关键词有“建模”“创新思维”“数学问题”,聚焦于将创新思维的培养融入数学建模教学。例如,宋涛结合教学经验对高中数学教学渗透数学建模思想谈了自身的体会,认为实施数学建模的教学是提高学生应用意识和创新能力的重要举措。[12]

#5初中数学是第六大聚类主题。中学包括初中和高中两个阶段,这一聚类的研究聚焦初中阶段,多以初中数学建模为研究主题。例如,藏武存认为初中教师应注重对初中学生数学建模能力的培养,由此探究了初中数学教学培养学生数学建模能力的方式方法。[13]

#6数学模型是第七大聚类主题。数学建模从字面解释就是建立数学模型,然后通过一定的方法对数学模型进行求解。因此,建立正确合理的数学模型尤为重要。该聚类的高频关键词有“数学模型”“建模思想”等,主要围绕与实际情景密切相关的数学模型进行探究。例如,罗问哲针对某高中教学楼在紧急情况下学生的疏散问题采用数学建模的思想建立了疏散模型,对安全疏散的最短时间进行了计算并给出了高效疏散学生的建议。[14]王茜等人认为数学建模能深化基础数学形成知识体系,避免学生陷入题海,并以具体的教学案例和数学模型分析了如何发展初中生数学建模思想。[15]

#7中学生是第八大聚类主题。该聚类主要包括“数学通报”“张思明”“散点图”等高频关键词。该聚类主要由影响力较大的学术期刊《数学通报》而形成,《数学通报》收录了较多的关于中学数学建模方面的文献,主要围绕中学生数学建模意识和能力的培养及其影响因素。例如,徐梦圆等人认为数学建模对中学生理解数学知识的本质及数学学科具有重要意义,由此探究了培养中学生数学建模核心素养的方法。[16]颛孙长宗等人对影响中学生建模能力提高的因素进行了分析并给出了提高中学生建模能力的对策。[17]

#8数学教学是第九大聚类主题。该聚类的研究也以数学建模的教育教学为主,与聚类#0数学建模的研究聚焦点基本一致。

#9不等式是第十大聚类主题。该聚类的高频关键词有“建模方法”“函数思想”“不等式”“二次函数”“数学语言”等,主要关注数学建模在实际生活情景中的应用,通过使用正确的建模方法,应用数学知识解决实际问题。比如,展青岗发现中考加强了对以数学建模为中心应用题的考查而学生在此方面的得分率相对较低,由此对中考例题几个常用的建模模型进行了讨论。[18]

通过以上对10个聚类的具体分析,经过人工阅读文献与归纳,中学数学建模领域的研究热点大致可总结为五个方面:中学数学建模教学(#0、#3、#5),学科核心素养下数学建模的教学实施(#1、#2),中学数学建模思想与方法(#4、#9),数学模型的建立与应用类问题(#6、#8),中小学数学建模意识和能力的培养(#7)。其中,前三个方面具有很强的相关性,都涉及中学数学建模教育。

四、演化路径

演化路径即研究发展脉络。CiteSpace软件在关键词聚类图谱的基础上可生成时间线图,进而对研究领域内热点主题的演化路径进行分析。演化路径在本质上是各聚类的关键词及其共现关系在时间轴线上的铺展呈现。经调整,本研究获得中学数学建模研究领域如图2所示的时间线图谱。此外,本研究对研究领域的关键词进行突现性检测,生成如图3所示的关键词突现图谱。

图2 时间线图谱

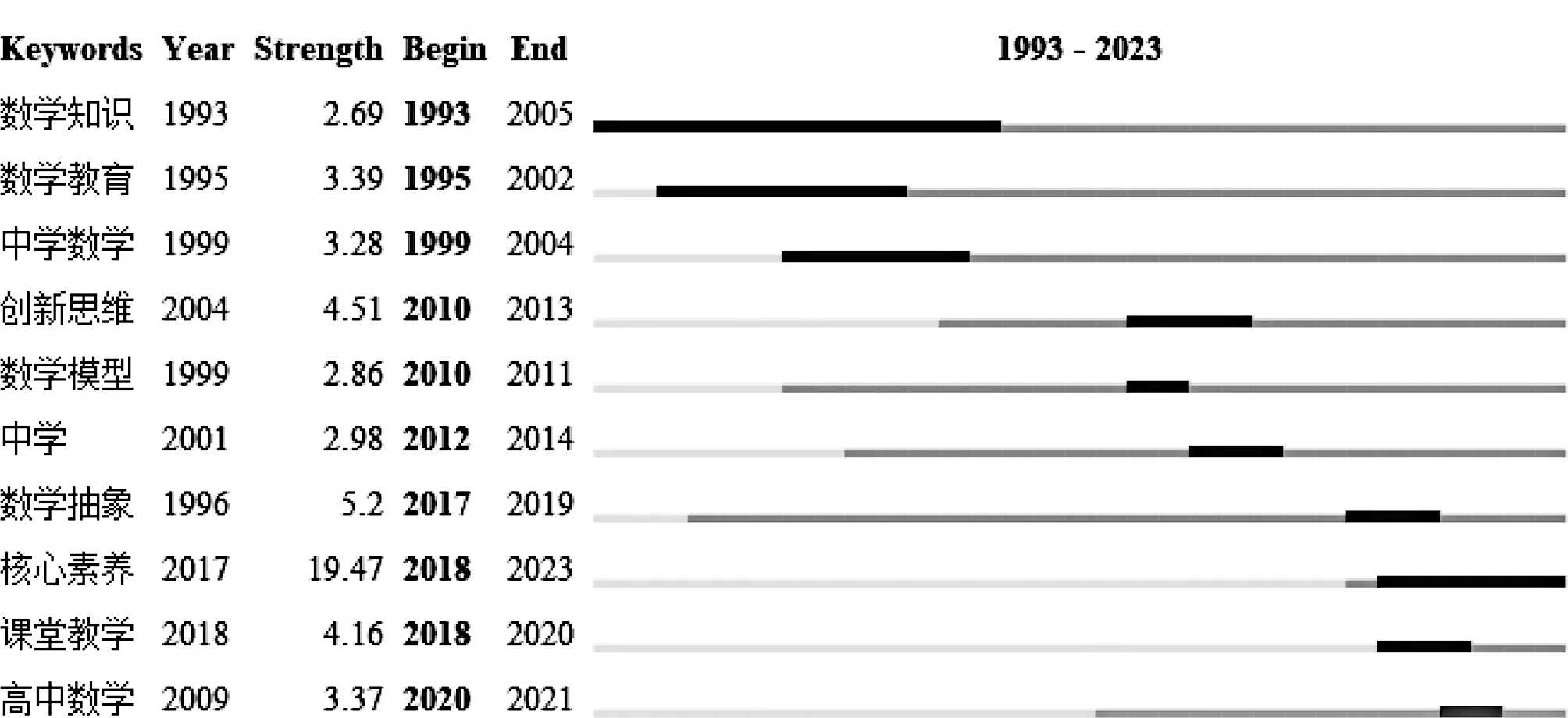
图3 关键词突现图谱

结合图2和图3的结果分析,我国中学数学建模研究大致可划分为三个阶段。

(一)基础发展阶段(1991—1999年)

该阶段的高频关键词主要有“数学建模”“数学知识”“数学应用”“数学教育”等,相关研究重点关注中学数学建模教学、中学数学建模课程及数学建模教材等方面。中学数学建模教学是重点中的重点,研究主要聚焦教学方法、教学意义、教学影响等。其中,从理论层面进行论述的较多,从实践上阐述的相对较少。对中学建模课程,研究主要关注如何在数学课程上融入数学建模的因素以培养学生数学建模素养,对数学建模进行设计和建设的研究占据多数。对数学建模教材,有研究分析了我国现有的中学数学教材并对数学建模思想的合理融入进行了探索;也有研究通过分析外国数学教材中数学建模相关内容设计的特点等,以对我国教材编写提供借鉴。关键词“数学知识”“数学教育”“中学数学”是该阶段出现的突现词,这三个突现词在一定程度上也说明了中学数学建模教育在该阶段相关研究中占据重要地位。“数学知识”的突现开始时间最早且跨度最长,说明该阶段也较为重视数学知识传授方面的研究。

(二)多样发展阶段(2000—2016年)

该阶段跨度较长,涌现出“创新思维”“建模思想”“应用能力”“素质教育”“教学策略”等大量的关键词,研究呈现多样化发展趋势。除继续关注中学数学建模教育教学外,该阶段研究也开始关注数学建模对学生思想和能力的促进作用,包括学生建模思想与能力、创新思维与能力、问题解决意识与能力、应用能力等。部分研究者研究了数学建模思维与能力的培养模式、方法等,也有研究者则调查和测评了学生思维和能力提升的效果。由图3可以看出,关键词“创新思维”从2010年开始突现,突现强度较高,说明对数学建模与创新思维的研究成为该阶段领域内研究者关注的重点。此外,该阶段早期的突现词还有“数学模型”“中学”,但突现时间不长。

(三)集中发展阶段(2017年至今)

《普通高中数学课程标准(2017年版)》将数学建模列为数学学科核心素养,这引发了研究者对数学建模的极大关注。由图3可知,“核心素养”以极高的突现强度于2018年开始突现,说明普通高中数学课程标准的颁布对中学数学建模的研究发展产生了极大的影响。“核心素养”的突现时间持续到数据采集之时,说明未来一段时间的中学数学建模研究仍会聚焦到数学建模这一核心素养的理论与实践研究。这一阶段的其他突现词如“数学抽象”“课堂教学”“高中数学”等,也都与普通高中数学课程标准的颁布密切相关。数学抽象也是数学学科核心素养之一,课堂教学则是贯彻落实学科核心素养育人要求的主要方式。因此,该阶段以数学学科核心素养为核心,是将数学建模聚焦于学科核心素养培养的集中发展阶段。

五、研究结论与展望

(一)研究结论

基于文献计量和内容分析的方法,本研究对我国中学数学建模领域的研究热点、演化路径及未来趋势进行了探究。研究结果如下:“数学建模”“高中数学”“核心素养”“数学模型”等是该研究领域出现频次较高的关键词;共形成#0数学建模、#1核心素养、#2数学抽象、#3中学数学等10个聚类关键词;大致分为发展起步阶段、多样发展阶段和集中发展阶段三个阶段。

(二)研究展望

突现词“核心素养”不仅在突现强度上遥遥领先其他突现词,而且突现时间一直持续到现在。此外,“核心素养”是关键词聚类生成的第二大聚类名称,基于核心素养实施数学建模教学是中学数学建模研究领域的热点主题。因此,未来中学数学建模研究应多聚焦此方面选题。除此之外,未来研究工作还应该注重以下三个方面。

一是加强全国性的交流与合作。未来研究应整合研究力量,发挥核心机构、核心作者的引领作用,带动中学数学建模研究的发展。加强全国性学者间的交流与合作,采取课题资助、学术交流、指导实践等多种方式加强不同地区、不同机构的协同研究,促进我国中学数学建模研究的发展。二是提倡研究范式的多样化。纵观我国中学数学建模研究,以定性研究为主,多从理论层面表达观点并提出建议,而实证研究相对较少。未来研究要多注重多种研究方法的结合运用,加强多元研究范式的融合贯通。三是提升中学数学建模研究的应用性。指导实践是研究的重要价值之一。中学数学建模研究大多围绕数学建模教学、学生数学建模思想和能力的培养等方面,提升中学数学建模研究的应用性,要注重将相关研究放在具体教育教学情境中。