明挖地铁车站围护结构变形分析
王龙

摘要:地铁车站施工过程中,其围护结构的变形情况会影响其稳定性。以郑州市至巩义市域铁路市政配套工程为研究对象,对其进行数值模拟,分析围护桩施工过程水平位移变化规律,得出以下结论:基坑施工过程中,围护结构上部受到现场施工条件、地下水、施工机械荷载等因素影响,而数值模拟为对地铁车站基坑施工理想状态下的计算,所以二者间得出的水平位移存在一定的差距,但其水平位移曲线变化趋势基本一致,且不同工况下的最大水平位移差值小于5mm。采用数值模拟对围护桩的水平位移进行计算,可行性较高。增大围护桩的桩径可有效降低其水平位移,提升结构的稳定性,但当其桩径较大时,其提升效果较不明显。
关键词:地铁车站;围护结构;水平位移;数值模拟
0 引言
围护结构的变形及稳定性对地铁车站施工的安全性至关重要,近年来,许多专家学者针对地铁车站围护结构的受力及变形特性开展相关研究。
张玉庭等人[1]以某地铁车站为研究对象,建立其三维数值模型,分析该车站围护结构的位移及内力变化情况,研究结果表明该车站的桩身最大位移为83.94mm。宁茂权等人[2]以某地铁车站基坑工程为研究对象,基于现场监测数据,分析该车站围护结构的变形规律,研究结果表明,该车站围护结构的最大位移出现在其结构中部。王正庆等人[3]建立地铁车站基坑工程有限元模型,分析各因素对其围护桩水平位移的影响规律,研究结果表明,基坑布置形式对其围护桩水平位移的影响较大。明成银等人[4]对某地铁车站深基坑工程进行现场监测,分析其围护结构的受力及变形规律,研究结果表明,围护方案对其结构的变形存在一定的影响。许树生等人[5]以某地铁车站为研究对象,采用FLAC3D软件,分析地铁车站施工工程下围护结构的变形特性,研究结果表明,开挖深度与其地表沉降呈正相关关系。
本文以郑州市至巩义市域铁路市政配套工程为研究对象,对其进行数值模拟,分析车站基坑施工过程中围护桩水平位移变化规律,研究桩径对其水平位移的影响。
1 工程概况
本研究以郑州市至巩义市域铁路市政配套工程地下二层岛式车站(双停车线)为研究对象。该车站主体长516.7m,标准段基坑宽20.1m,深16.59m,扩大端基坑宽24m,深18m。
中心里程为DK6+885.189,起点里程DK6+456.389,终点里程DK6+973.089。车站标准段底板埋深16.59m,盾构井段底板埋深22.21m。
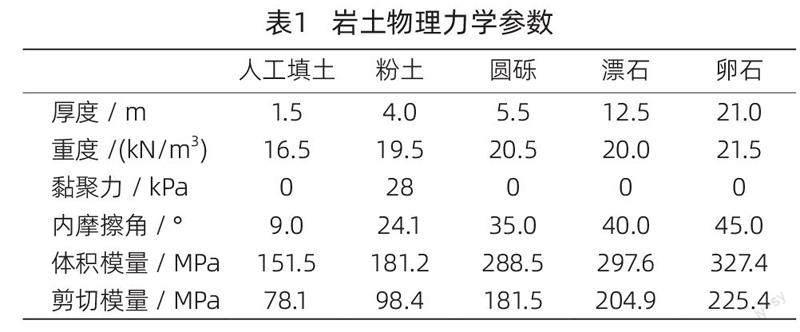
本车站为地下二层两跨箱形框架式结构(局部两层三跨),车站采用明挖法施工,基坑采用φ1000@1500围护桩(局部加密)+内支撑的支护型式,采用三道钢支撑(局部加一道钢支撑换撑)。车站两端区间均采用盾构法施工,小里程端盾构接收、大里程端盾构始发。车站附属采用明挖法施工。该地区的岩土物理力学参数如表1所示。
2 基坑围护结构数值模拟
为分析地铁车站施工过程中,其围护桩的位移变化规律,采用有限元软件对其水平位移进行计算。该地铁车站的施工工序主要分为四步,分别对应四种工况。
工况一(第一步):施工接地网、垫层、防水板、防水保护层、底板及部分侧墙。
工况二(第二步):待底板、侧墙混凝土强度达到设计强度的85%,分段拆除第三道撑,施工地下二层侧墙防水层及侧墙、中隔墙、结构柱、中楼板梁、中楼板。
工况三(第三步):待中板、侧墙混凝土强度达到设计强度的85%,分段拆除第二道撑,施工地下一层侧墙防水层、侧墙、结构柱、顶板梁、顶板及压顶梁,施工顶板防水层。
工况四(第四步):待顶板、侧墙混凝土强度达到设计强度的85%,分层回填至第一道钢支撑下后,拆除第一道钢支撑,分层回填顶板上覆土,施工内部结构,完成车站主体结构。
3 变形规律分析
为分析施工过程中围护桩的变形规律,采用有限元软件,对地铁车站的围护桩水平位移进行计算。
3.1 不同工况下水平位移-深度曲线
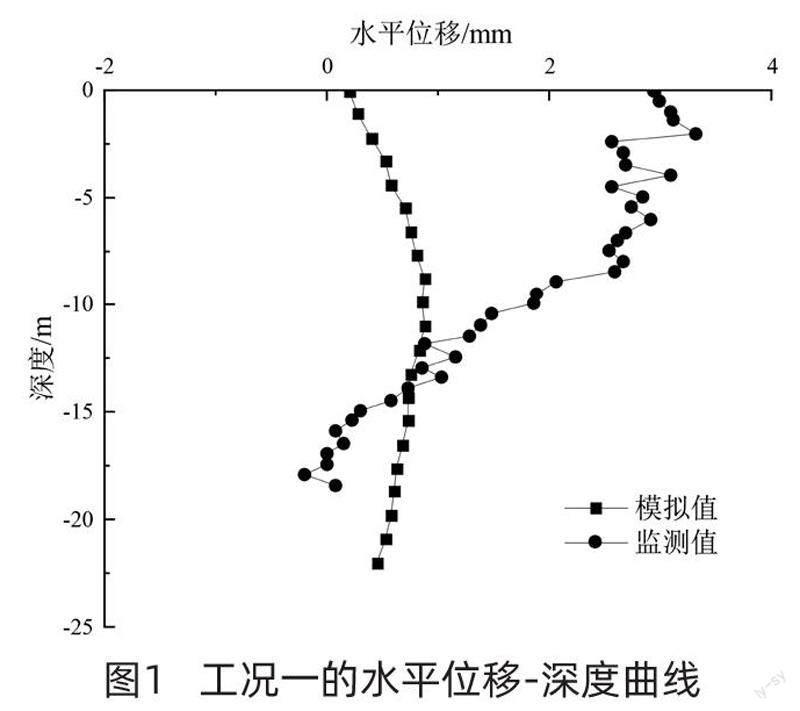
3.1.1 工况一的水平位移-深度曲线
工况一的水平位移-深度曲线如图1所示。由图1可知,随着深度的增大,围护桩的水平位移模拟值呈先增大后减小的趋势,但其曲线变化趋势较为平缓,围护桩水平位移监测值与模拟值的变化趋势具有一定的差异性。
随着深度的增大,其水平位移逐渐减小。当深度较小时,围护桩水平位移的模拟值与监测值差值较大,且其最大差值为2.86mm,随着深度的增大,二者间的差距逐渐减小。当深度小于12m时,围护桩水平位移监测值大于其模拟值,这是由于地铁车站施工过程存在不稳定因素,而数值模拟为对地铁车站施工理想状态下的计算,所以其位移较小。
3.1.2 工况二的水平位移-深度曲线
工况二的水平位移-深度曲线如图2所示。由图2可知,随着桩深的增大,围护桩的水平位移监测值与模拟值均呈减小趋势。当深度为0m时,其水平位移有最大值,模拟值与监测值分别为3.87mm、4.03mm,说明在工况2下,围护桩的变形主要发生于其桩顶。
当桩深较小时,水平位移模拟值的减小趋势较为明显。随着深度的增大,当深度大于12m时,其水平位移-深度曲线变化趋势较为平缓。而监测值的水平位移在深度较小时变化趋势较为平缓,当桩深大于8m时,其水平位移变化趋势较为显著。
對比工况一可得,工况二的最大水平位移为4.87mm,大于工况一的最大水平位移,说明随着施工过程的进行,地铁车站的围护结构发生的变形逐渐增大。
3.1.3 工况三的水平位移-深度曲线
工况三的水平位移-深度曲线如图3所示。由图3可知,随着深度的增大,围护桩的水平位移呈先增大后减小的趋势。当深度为8m时,围护桩的水平位移模拟值与监测值均存在最大值,其值分别为9.75mm、6.54mm。
对比工况一与工况二可得,工况三的水平位移-深度曲线的变化趋势与以上两种工况存在一定的差异性,工况一与工况二的最大水平位移集中于围护桩桩顶,而工况三的最大水平位移集中于其中部。由此说明,随着施工过程的进行,地铁车站围护桩的变形特性会发生一定的变化,其危险部位由围护桩桩顶转移至围护桩中部。
3.1.4 工况四的水平位移-深度曲线
工况四的水平位移-深度曲线如图4所示。由图4可知,工况四的水平位移变化规律与工况三具有一致性,其水平位移-深度曲线呈拱型变化。当深度为8m时,工况四的水平位移有最大值,其模拟值与监测值分别为10.68mm、8.73mm。
在工况四下,当深度小于12m时,围护桩的水平位移较大,说明围护桩的中上部发生的变形较大,此段的稳定性较差,易发生破坏。
3.1.5 各工况综合分析
综合以上分析可得,各工况的水平位移监测值与模拟值间存在一定的差距,且当深度小于12m时,二者间的差值尤为明显。
分析认为,由于基坑开挖过程中,圍护结构上部受到现场施工条件、地下水、施工机械荷载等因素的影响,而数值模拟为对地铁车站基坑施工理想状态下的计算,所以二者间得出的水平位移存在一定的差距。但二者间的水平位移曲线变化趋势基本一致,且不同工况下的最大水平位移差值小于5mm,为此采用数值模拟对围护桩的水平位移进行计算可行性较高。
3.2 不同桩径下水平位移-深度曲线
在实际工程中,围护桩的变形情况常受到许多因素的影响,为分析围护桩直径对其变形情况的影响,计算得出不同桩径下的围护桩水平位移-深度曲线,如图5所示。
由图5可知,不同围护桩直径的桩深水平位移变化规律具有一致性,其水平位移与其桩径呈正相关关系。当围护桩的桩径较小时,不同桩径间的最大水平位移差距较大。其中,桩径为0.6m与桩径为0.8m的围护桩最大水平位移差值为56mm。
随着桩径的增大,不同桩径间的水平位移差距较不明显。其中,桩径为1.2m与桩径为1.4m的围护桩最大水平位移差值不足1mm,说明增大围护桩的桩径可有效降低其水平位移,提升结构的稳定性,但当其桩径较大时,其提升效果较不明显。
4 结束语
本文以郑州市至巩义市域铁路市政配套工程为研究对象,对其进行数值模拟,分析车站基坑施工过程中围护桩水平位移变化规律,研究桩径对其水平位移的影响,得出以下结论:
工况一下,随着深度的增大,围护桩的水平位移模拟值呈先增大后减小的趋势,但其曲线变化趋势较为平缓,围护桩水平位移监测值与模拟值的变化趋势具有一定的差异性,随着深度的增大,其水平位移逐渐减小。
工况一与工况二的最大水平位移集中于围护桩桩顶,而工况三的最大水平位移集中于其中部,说明随着施工过程的进行,地铁车站围护桩的变形特性会发生一定的变化,其危险部位由围护桩桩顶转移至围护桩中部。
不同围护桩直径的桩深水平位移变化规律具有一致性,其水平位移与其桩径呈正相关关系。当围护桩的桩径较小时,不同桩径间的最大水平位移差距较大。增大围护桩的桩径可有效降低其水平位移,提升结构的稳定性,但当其桩径较大时,其提升效果较不明显。
参考文献
[1] 张玉庭,朱思儒.地铁车站深基坑围护结构稳定性研究[J].房地产世界,2021(19):20-22+34.
[2] 宁茂权,贺湘灵,王涛,等.沿江地铁车站围护结构变形规律现场实测分析[J].铁道建筑技术,2020(6):40-43.
[3] 王正庆,郭运华,石振宇,等.光谷五路地铁车站基坑围护桩顶水平位移的控制机制[J].土工基础,2020,34(1):17-20.
[4] 明成银,程荷兰,胥稳,等.地铁车站深基坑施工围护结构及周边环境监测与分析[J].山西建筑,2019,45(9):64-65.
[5] 许树生,侯艳娟,刘美麟.天津地铁6号线车站深基坑开挖下围护结构及墙后地表变形特性分析[J].北京交通大学学报,2018,42(1):25-33.

