离散选择实验潜类别logit模型在卫生服务领域的应用与Stata软件的实现*

张春丽 邱佳玲 陈 莎 刘仲琦 古羽舟 鲁永恒 邓瑜,6 郝春,6△ 郝元涛,6

【提 要】 目的 简要介绍离散选择实验的设计步骤和潜类别分析模型的基本原理,通过实例演示介绍潜类别logit模型在Stata中的实现过程,为该模型在离散选择实验中的实际应用提供方法学的参考。方法 基于广州市艾滋病高危人群选择HIV自检试剂偏好的离散选择实验数据,通过实例演示潜类别logit分析模型的构建过程,并提供相应的Stata命令。结果 最终确立了4个类别模型为最优分类,模型估计结果显示4个类别模型中类别1(偏好尿液试剂),类别2(偏好更便宜的血液试剂配套说明书讲解和自行判读结果),类别3(偏好更便宜的尿液试剂),类别4(偏好血液试剂配套视频讲解和专业人员判读结果)的差异具有统计学意义。结论 潜类别logit模型用于离散选择实验数据的分析具有简便性与灵活性,但也有其应用的局限性,因此需要进一步结合其他模型来优化分析。

离散选择实验(discrete choice experiment,DCE)是一种多因素变量的分析方法,目前已广泛用于市场研究、运输经济学、心理学以及卫生服务利用等领域,以了解个体偏好。而个体对于某一商品或者服务的偏好可分为基于现实场景的显示性偏好和基于假设场景的声明偏好,显示性偏好即在实际生活中对于已经确定属性特征的商品或者服务的偏好,例如出行时对交通工具的选择。而在声明偏好中,商品或者服务的属性特征组合是假定的,例如某运营商提前设置了假定的套餐A和套餐B来调查客户对话费的选择偏好。衡量显示性偏好常用的为传统问卷调查,而离散选择实验则是衡量声明偏好的典型方法,其可以提供影响决策者选择的各种商品或者服务特征相对重要性的定量信息[1]。

对于离散选择实验数据的分析,目前常用的有基础的多项logit模型(multinomial logit model,MNL)、混合logit模型(mixed logit model,MXL)和潜类别logit模型(latent class model,LCL)等。在应用研究中,传统的多项式logit模型需要遵循无关选择独立性(independence of irrelevant alternatives,IIA)假设,即删除或者添加因变量中的类别不会影响剩余类别的选择概率,然而在实际情景中,参与者做出的选择决策之间往往呈现出一定的相关性,会违背IIA假设,因此多项式logit模型已经不适用于现实情况的分析,也无法处理随机偏好差异[2]。但解释个体选择偏好的差异至关重要,即一些人比另一些人会更关心特定的产品属性[3]。并且了解目标群体对特定商品或者服务的偏好异质性有助于决策者调整和多样化他们的项目,以更好地匹配目标人群的需求[4],因此选择其他的logit模型才能使得分析更加精细化。混合logit模型和潜类别logit模型则能弥补该方面的不足,但混合logit模型需要事先假定参数的分布形式,从而导致在应用中受到限制。而潜类别logit模型则不需要对参数进行任何假设,其从群体层面解释异质性,尤其在关于人群细分的研究中成为主流方法[5]。

潜类别模型的基本原理

社会科学领域一些比如智力、人格、社会经济地位等概念往往不能直接测量,这些变量被称为潜变量,根据其分布形态可以分为连续型和离散型,当潜变量为连续型时,可根据外显变量是连续型和离散型分为因素分析和潜特质分析;当潜变量为离散型时,则根据外显变量是连续型和离散型分为潜剖面分析和潜类别分析。潜类别模型是通过构建潜变量估计外显指标间的关联,并对目标人群分类[6],进而解释研究对象群体的异质性对于外显指标的影响[7],其假设潜变量X有t(t=1,2,…,T)个类别,A、B、C是三个外显变量,且其水平数分别为I,J,K,可以表示为:

(1)

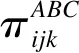
潜类别logit模型的原理

潜类别logit模型是基于潜类别模型的理论将人群细分后,结合多项式logit的似然函数进行偏好参数的估计,即基于偏好中未观察到的或“潜在的”异质性来识别参与者类别[10],考虑了每个对象做出的多种选择,并根据他们的选择模式随机分配其到有限的C类集合中(其中C是类别总数)。在同一类别内[11],参与者被假定偏好相同,而在类别及其亚组间有不同偏好,并且每个类别都有自己特定的偏好参数(效用函数),β=(β1,β2,…,βC)[12]。分析过程主要包括最优模型构建、模型拟合以及参数估计与解释。

1.最优模型构建

在经验应用中,通常通过检验信息准则(如贝叶斯信息准则(BIC)和一致性Akaike信息准则(CAIC))来选择最优的潜类别数,BIC=-2lnL+mlnN,CAIC=-2lnL+m(1+lnN),其中lnL是最大样本对数似然,m是拟合模型参数的总数,N是所研究数据集中的决策者数。BIC和CAIC通过使用随决策者数量N增加而增加的补偿函数,对具有额外参数的模型进行更严厉的补偿。BIC和CAIC均建立在似然比卡方检验基础之上,可用于比较对参数进行不同限制的模型,两者均以越小表明适配度越好[13-14]。

2.模型拟合

为了更好地解释潜类别logit模型,在这里先简单介绍传统多项式logit的建模,理论基础为随机效用理论,其效用函数Uij可以表示为:

Uij=Vij(β)+εij

(2)

Uij表示个体i选择备选方案j的效用,其中i=1,…,n;j=1,…,k。Vij(β)是解释变量的参数线性组合,β是一个参数向量,εij是误差项,是服从Gumbel分布的随机变量,则个体i选择方案j的概率为[15]:

(3)

最大似然法(maximum likelihood,ML)可估算得到方程(2)中的系数,来表示各因素对选择偏好的影响。

潜类别logit模型也主要采用最大似然法进行参数估计,其迭代过程常用的算法有EM(expectation-maximization)、NR(Newton Rapson)等算法,其中 EM 算法最为常用。潜类别logit模型构建如下:在类别C中,假设决策者n(n=1,2,3,…,N)在每个假设场景T中都面对J个备选。ynjt表示一个二元变量,如果决策者n在假设场景t中选择备选j,则该变量等于1,否则等于0。在场景t中可供决策者选择的备选j被具有K个属性的xnjt所描述。βC为K系数的列向量,可以解释为xnjt中相应条目的边际效用。则决策者n的T个选择的联合概率Pn为[14,16]:

(4)

3.参数估计与解释

使用潜类别logit模型对离散选择实验数据进行估计,会得出该类人群对所关注商品或服务某一特征属性的选择偏好参数β,β=(β1,β2,…,βC),数值为正,表示相对于参照水平,更偏好于选择当前水平;数值为负,则表示更倾向于选择参照水平,从而可了解每一类人群的选择偏好。

实例分析

1.HIV自检试剂盒的离散选择实验

离散选择实验的设计步骤主要有[18]:(1)确定商品或者服务的属性及其水平;(2)构建选择集及其选项方案,形成DCE问卷;(3)数据收集与整理;(4)统计分析与结果解释。本研究确定了HIV自检试剂盒的4个属性,3个2水平,1个4水平,分别为样本类型包括血液和尿液,操作说明方式包括说明书和视频讲解,结果判读方式包括自行判读和专业人员判读,价格包括0元、20元、50元和80元。通过部分因子设计创建了8个选择集(选择集的创建参考文献[18]),每个选择集含有两个选项方案。表1展示了经过以上设计而产生的一个选择集及其两个选项方案试剂盒A和试剂盒B的示例,其他7个选择集差别在于两个选项即试剂盒类型的不同,比如下一个选择集其两个选项可能为试剂盒C与D。调查在广州市岭南伙伴社区HIV检测咨询服务点开展,最终收集问卷200份。

表1 离散选择实验设计的选择集示例

2.数据整理格式

传统的数据即宽型数据,其排列格式为一行数据对应一个样本,如表2,在第一个样本中(PID),收入取值为2(5000～10000元),选择集1的选择为1(试剂盒A),选择集2选择为2(试剂盒D)。同理第二行对应第二个样本的相应各变量取值。而在离散选择实验中,宽型数据无法展示商品或者服务的属性变量,如HIV检测试剂盒的样本类型(血液或者尿液),并且因变量为8个选择集的选择结果,在宽型数据中只能横向排列,在一列中无法进行体现,因此需要整理成长型数据,以本研究为例(文件:DCE样本数据.dta),整理形式见表3,一个样本对应多行数据。前两行则表示PID为1的样本,在GID为1的选择集(包含两个选项1和2)中进行选择,两个选项为试剂盒A和试剂盒B,根据表2中两个试剂盒的配套情况,则可得试剂盒A对应第一行,其血液、说明书与自行判读几个变量的值为1,价格变量的值为0元,而第二行对应试剂盒B。在表3倒数第二列也即模型的因变量中,第一行的值是1,第二行是0,说明选择了试剂盒A,同样第三、四行对应选择集2中试剂盒C与D。一个体(PID)会在相同的8个选择集(GID)中选择,因此一个样本会产生8×1×2=16行数据,并且PID为9～16的选择集的各试剂盒属性是PID为1～8的重复,不随个体变化。其中HIV试剂盒属性中样本类型(血液和尿液)、操作说明方式(视频讲解和说明书)和结果判读方式(自行判读和专业人员判读),均是无序二分类变量,因此进行了虚拟变量设置(即血液的取值为1,尿液的取值则为0),并将其中一个分类作为参照,模型分析时仅代入非参照类别。价格是连续性变量可直接代入。个体属性收入会随PID变化。(附:本研究所用数据与代码链接:https://pan.baidu.com/s/1CycvmsY-wtKVw70o_uptlg,提取码:zsdx)

表2 传统宽型数据的形式

表3 离散选择实验长型数据排列格式示例

3.潜类别logit模型过程在Stata实现步骤

(1)最优模型的建立

该过程使用Stata的外部命令lclogit来实现,其返回列表中保存了信息标准BIC和CAIC。表4列出了6种分类模型的适配估计指标,Classes为类别数,若Classes为3,表示根据某种潜在特征将研究对象分为3个类别,Classes最小为2,可以看到当分类模型的类别数目越多,BIC与CAIC的值逐渐减少,到Classes为5时又开始上升,在Classes为4时CAIC与BIC均到达最小,分别为1276.306和1254.306。因此考虑可选择4个类别作为最优分类模型。

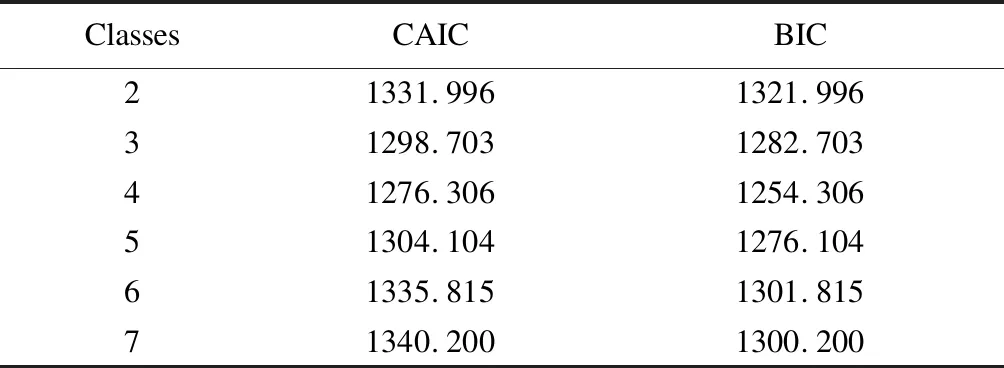
表4 Stata输出模型分类数目及其适配估计指标

确定了最优分类模型后,接下来调用Stata的另一个外部命令lclogit2[16]来估计最优分类模型即4个类别模型中类别1～4(Class 1～4)对应的模型估计系数和类别分布比例。模型估计系数为正,则说明该类别人群对于HIV自检试剂属性水平的偏好可能大于其参照;系数为负,则可能更偏向于参照;价格的系数为负,表明可能更倾向于便宜的试剂。以样本类型为例,Class 1的系数为1.611,说明相对于血液,该类人群可能更加偏向于尿液。价格的系数在4个分类中均为负,说明了Class 1～4都可能更愿意选择便宜的试剂。同时还可以知道200个参与者在Class 1,Class 2,Class 3和Class 4中的分布比例分别为0.222,0.602,0.124和0.052,详见表5。与潜类别logit模型每个解释变量对应每个类别都会有其参数估计值不同的是,多项式logit模型没有对研究群体进行类别区分,参数估计建立在整个人群上,每个解释变量只对应一个参数。

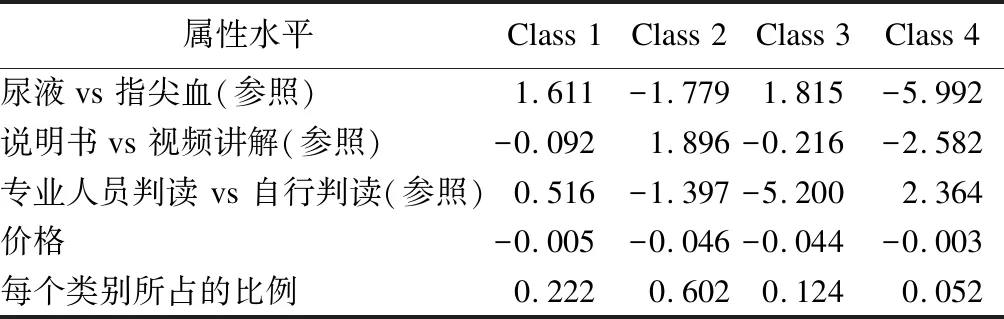
表5 4类别模型对HIV检测试剂各属性水平偏好的参数估计及类别分布比例

(2)参数估计及解释

前面初步得出了每一类别各属性特征的模型估计参数,同包括多项式logit在内的其他logit模型相同,选择偏好是否具有显著性差异还需要对值与参数的P置信区间进行估计,可通过Stata中的lclogit2ml命令来进行,结果如表6,可以得出对样本类型的偏好差异,Class 1(β=1.611,95%CI:1.108～2.113,P<0.001)和Class 3(β=1.830,95%CI:0.336～3.324,P=0.016)更愿意选择尿液,而Class 2(β=-1.772,95%CI:-2.490～-1.054,P<0.001)和Class 4(β=-5.993,95%CI:-9.190～-2.796,P<0.001)更倾向于血液;对于操作说明方式,Class 2更愿意选择说明书(β=1.893,95%CI:1.028～2.758,P<0.001),而Class 4则偏向于选择视频讲解(β=-2.582,95%CI:-4.866～-0.297,P=0.027);而在结果判读方式上,Class 2更愿意选择自行判读(β=-1.404,95%CI:-2.593～-0.214,P=0.021),而Class 4则偏好选择专业人员判读(β=2.364,95%CI:0.168～4.561,P=0.035);在价格方面,Class 2(β=-0.046,95%CI:-0.062～-0.030,P<0.001)和Class3(β=-0.044,95%CI:-0.088～-0.001,P=0.045)均更加倾向于便宜的试剂。

表6 HIV自检试剂各属性水平偏好的潜类别logit模型估计

而根据表5结果可知Class 1(22.2%)和Class 2(60.2%)人群占比较高,提示了这两类艾滋病高危人群尿液和血液自检试剂偏好提供配套的服务特征:Class 1偏好尿液自检试剂配套视频讲解并由专业人员判读的服务;Class 2偏好血液自检试剂配套说明书并由检测者自行判断的服务。

讨 论

基于以上说明和案例,可见潜类别logit模型能够基于潜在的变量将群体进行分类,并解释类别间偏好的异质性。按照个体“潜在”特征来进行分类,只假定个体被隐含地分在某个类别中,并且潜类别logit模型没有对这种潜在异质性的形式做出任何假设,参数的效应在同一类中相同而在不同类之间变化[2],这也使其在实际应用中更加灵活。但是其需要事先假定分类数,分类数目过多会导致模型不收敛,同时由于是在群体层面,故无法分析群体内个体的异质性。而分析偏好异质性的另一个常见模型混合logit模型则是从个体层面进行分析,允许解释变量的系数是随机的,但需要通过设定模型系数服从一定的分布,并估计出相应的分布参数[5],而且虚拟变量的设置会导致模型不收敛,该模型的详细方法可查阅McFadden[19]等的文章。总体而言,两个模型处理随机偏好的结果虽然比较相近,但多数研究表明潜类别logit模型在拟合性、理论基础、信息丰富度等方面还是略优于混合logit模型[5]

每个模型都有其自身的优缺点,因此国外有关离散选择实验的研究中分析异质性对于选择偏好的影响常为两个或多个模型的联合对比使用或者混合建模,以减少单用一个模型带来的限制。并且随着研究的深入,衍生更多复杂的模型如随机参数潜类别模型,马尔科夫转换模型等也会使分析更加优化。本文介绍了潜类别logit模型的基本理论,结合离散选择实验演示了该模型的建立与分析以及在Stata 中实现的过程,也为其他领域的相关研究提供借鉴。