常规岩土力学试验主应力组成分析与疲劳仿真验证

张苗苗，徐鑫磊，于宏波

（赤峰昊林工程勘察设计有限公司，内蒙古 赤峰）

1 常规岩土力学仿真中的主应力分布特点

为实现对岩土力学试验的仿真，开展研究前，引进 Mohr-Coulomb （莫尔 - 库伦强度理论）、Drucker-Prager（DP 准则），将其作为参照，进行岩土材料在力学性能试验中应力分布的研究[1]。

在此过程中，Mohr-Coulomb 理论提出，材料发生破坏行为，大多属于剪切破坏，在此种条件下，破坏面上存在剪应力，而对应的剪应力可以用法向应力函数表示，表达式如下：

式中：τf代表材料发生破坏时，破坏面上的剪应力；f（σ）代表法向应力函数。根据上述函数，可以确定岩土材料的莫尔破坏包络线，如图1 所示。

图1 岩土材料的莫尔破坏包络线

图1 中，A、B 代表破坏面的两个莫尔圆；O1、O2代表两个任意点莫尔圆半径；M、N 代表破坏面的垂直包络线[2]。设定一个参数为岩土材料的屈服系数，将其表示为Q，Q 的计算可以通过下述公式得到。

式中：Q 代表屈服系数；O1 代表任意点莫尔圆半径；O1M 代表圆心到包络线距离。根据实际情况，应明确Q 的取值在0～1 之间，当计算后发现Q 的值＞1 时，说明在此种条件下，岩土材料样件已在法向应力作用下，达到了屈服破坏程度。

在上述内容的基础上，参照DP 准则，进行岩土材料屈服应力的分析，在此过程中，可以将岩土材料的样件假设为一个三维模型，模型在三个方向的主应力构成三维应力空间[3]。在此种条件下，岩土材料样件中对应某一节点的主应力可以用（σ1, σ2,σ3）表示，在此种状态下，样件的应力状态可以用主应力空间中的随机一点P 表示[4]。将主应力空间划分为若干个平面，随机一个主应力平面上都应当存在正向应力分量，但无论分量如何发生变化，第一主应力都应当保持不变，此时，第一主应力可以用下述公式计算得到。

式中：I1代表第一主应力。

在此种条件下，主应力主要由平面上的剪应力构成，剪应力计算公式如下：

式中：τπ代表平面上的剪应力；J2代表第二偏应力不变量。

完成上述计算后，以岩土力学试验中的有限元仿真试验为例，进行主应力分布特点的具体分析[5]。在此过程中，采用数值计算的方式，进行力学试验中相关数值的模拟，计算过程中，可按照表1，设定岩土力学试验中岩土材料样件对应有限元模型的技术参数。

表1 岩土力学试验中岩土材料样件对应有限元模型的技术参数

研究过程中，进行建立带模板与不带模具的仿真结构模型，将两个模型标注为①、②，对样件的底部节点施加全约束，将其顶部与竖向垂直方向发生耦合，在顶部的中心节点位置，施加一个垂直向下的作用力，将其作为主应力，构件的主应力分布如图2 所示。

图2 主应力分布云图

2 疲劳仿真验证

2.1 建立疲劳仿真计算模型

通过上文试验获得主应力组成，将其大致分为三个部分，分别为：单轴贯入中的纯压分布、双轴贯入中的纯拉分布和纯剪中的拉压复合应力组成。结合上述得到的主应力组成方式下的疲劳荷载仿真算例，实现对研究试件在疲劳荷载方式下的主应力分布情况分析。该计算实例是一种以拉、剪、压为交变应力的弹塑性材料为研究对象，以有限元方法模拟其疲劳加载特性。具体如图3 所示。

图3 疲劳仿真计算模型

该模型是一种长方体，其长为101 mm，宽为50 mm，厚度为50 mm。该疲劳仿真计算模型的弹性模量设置为2.03×105MPa，泊松比设置为0.2。在进行疲劳仿真的过程中，将模型的边界条件设置为：左半边上、下表面的节点Y 向限制，左顶面X 向连接，右半边上、下表面的节点Y 向连接。在施加力时，设计对左部顶面一个恒定压力或拉力，即将模型X 轴正向或负向作为施压方向。在模型右部地面按照时间的变化重复施加沿Y 轴方向的推力，该力为剪切力。按照上述操作循环加载，实现对研究试件疲劳荷载的施加。图4为疲劳仿真计算模型加载方式示意。

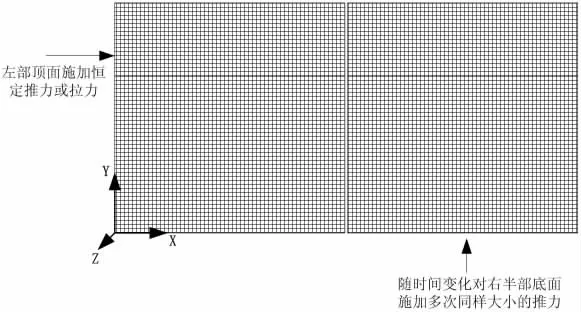
图4 疲劳仿真计算模型加载方式示意

图5 为对研究试件左部顶面时间恒定拉力或推力，施加的剪力循环荷载随时间的变化曲线。

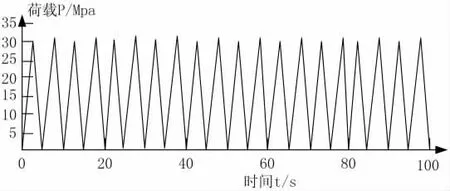
图5 疲劳仿真计算模型循环荷载大小变化

从图中可以看出，随着时间的不断增加，荷载呈现出明显的先增加后降低，且不断循环的变化规律。调节循环载荷中常压或常压的推动力或拉力的正负和值，并调节所受剪切力的值，通过比较分析，得出对应的2 D 应力莫尔圆，从而得出在拉剪、压剪等疲劳载荷作用下，各工况下的主应力构成模式。

2.2 仿真算例设置与结果分析

本研究设置多组拉力或压力与循环剪力之间的组合形式，最终选出如表2 所示的四组作为对比分析的研究对象。

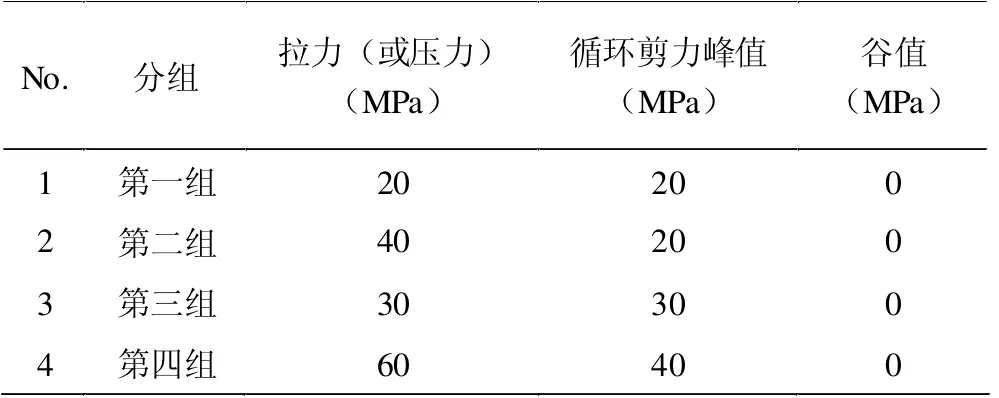
表2 对比分析算例参数设置

针对第四组算例，增加其循环次数，并进行计算。被研究试件受到恒定拉力和循环剪力的作用。结合其特点，为方便更直观对比，需要先将机组不同算例中某一循环内的剪力分别施加到峰值水平和谷值水平，对试件的最危险节点下剪应力和塑性剪应变进行对比。针对第一组算例，在仿真过程中发现，在恒定拉力的取值为20 MPa 时，此时在拉剪状态下，当循环剪力峰值和谷值不断变化时，最危险节点的最大剪应力为112.8 MPa，压剪状态下，最大剪应力为125 MPa。在恒定拉力设置为20 MPa 和恒定剪力设置为20 MPa条件下，最大塑性剪力应为2.5×10-4，而在第一个周期达到2.5 s 后，塑性应变不再增加。因此，可认为该周期内，试样仍处在塑性应变阶段。在仿真中，当恒定压力设定为20 MPa，剪力为20 MPa 时，相同的循环至剪力峰值时最大塑性应变为2.4×10-4，在第一个周期峰值时间为2.5 s 时塑性剪应变也不再增加，因此在这种状态下，试件也未达到塑性应变状态。在该组算例中，拉剪状态下最危险节点受剪应力较小，但塑性剪应变较大。

针对第二组算例，在仿真过程中发现，当一个恒定的张力被设定为40 MPa 时，剪切力被设定为20 MP。在拉伸- 剪切状态下，最大剪切应力是117 MPa，在对应的情况下，压力状态下，最大剪切应力是116 MPa。由此可以看出，在这一组实例中，最危险的结点所受剪切力的幅值相差不大。恒定压力设置为40 MPa，循环时间在2.5 s 时，此时塑性剪应变不再增加，说明在该组算例当中没有出现塑性应变。

针对第三组算例，若将不变的张力设定在30 MPa，则剪切力的峰值是30 MPa。在拉- 剪作用下，最危险的结点所承受的最大剪切力为142 MPa，剪切应力随循环数的增加而降低。在对应的情况下，最危险的节点在受压剪切状态下，其最大剪切应力为162 MPa。由此可以看出，在该组算例当中，压剪状态下所受的剪应力较大。在恒定拉力为30 MP，剪力为30 MPa 时，此时试件开始出现了塑性应变，塑性剪应变从0 逐渐增加到1.9×10-3。在相同条件下，压剪状态下最危险节点的最大塑性剪应变为1.75×10-3。由此可以看出，当剪力循环到谷值时，拉剪状态下最危险节点的剪应变与压剪状态下的最危险剪应变相比更大。

针对第四组算例，为获得更明显对比效果，将循环次数增加到100 倍。对仿真结果进行分析得出，当恒定的张力设定为60 MPa 时，剪切力的峰值为40 MPa，在拉- 剪切状态下，最危险的节点的最大剪切应力为170 MPa。剪切应力随循环数的增加而降低。在对应的情况下，最危险的节点在受压剪切状态下，其最大剪切应力为200 MPa。由此可以看出，该组算例中，在压力作用下，剪切应力是比较大的。

结束语

目前，国内外已经进行了大量的单轴和三轴的抗压、剪切和模型试验，并在阶段性的工作中，取得了丰富的实验资料与研究成果。为实现对此方面内容的优化，本研究从理论层面，对此方面工作进行深入分析。明确基于弹性理论下，应用力学中普遍存在的强度判据，找出试验中主要应力组成模式间的内在联系和规律。为落实此方面的研究，本研究开展了此次研究，完成研究后，初步明确了在岩土材料构件中主应力的分布规律，并掌握了材料的疲劳性能。本次研究经过大量的时间与查阅文献，初步取得了一些价值性成果，但研究得到的最终结果仍然受到试验中仪器设备、人员精力等相关因素的影响，导致试验与研究得到的部分结论仍有待进一步的完善、优化，因此，本研究将在此次研究中，结合相关工作的具体需求，选择更多形状的不同，设定不同的参数为变量，在多位置、多参数下，进行岩土材料样本构件在外部荷载条件下寿命的计算，希望通过此次的设计与研究，为后续技术人员的相关研究提供全面、进一步的技术指导与数值支撑。