面向探测效能增强的导弹路径规划方法*

张晓天，奚 勇，刘怡青，赵长春，孟海洋

(1. 上海航天控制技术研究所·上海·201109；2. 上海航天技术研究院·上海·201109；3. 陕西省肿瘤医院·西安·710061)

0 引 言

随着对空作战博弈对抗强度的增加，导弹飞行末段面临雷达、红外等多源复杂干扰情况下，如何提升导引头在干扰环境下的目标截获能力已成为国内外研究重点问题。以红外空空导弹为例，为提升导引头探测抗干扰能力，现有研究以提高导引头干扰识别算法性能较多，如引入智能算法提升抗干扰能力[1]。从文献[2]目标机动和干扰投放方式对红外空空导弹抗干扰效果分析可知，抛投诱饵需要在目标和导弹之间形成持续遮挡才能对导弹形成有效干扰。综上可见，导弹需要改变飞行路径以减少干扰对目标的遮挡时间，才能增强导引头目标探测效能，实现干扰环境下的目标捕获。

路径规划目的是得到一条满足多种约束条件的优化路径，国内外研究者已针对无人机[3-5]、无人车[4-6]、巡航导弹[7-9]等运动平台开展大量研究。在无人机路径规划研究中，张晶晶[3]等人采用排序蚁群算法实现障碍环境下的无人机路径规划，考虑飞行器转向角约束，避免了路径出现折返和尖角。ZHOU[4]等人采用改进蝙蝠算法实现复杂环境下无人机三维路径规划，通过与多种群优化算法对比展示了该方法的优越性，但该方法只适用于静态障碍环境。针对复杂动态威胁环境，YAN[5]等人采用深度强化学习规划无人机路径，通过在已知地图环境下训练深度神经网络得到动作Q值，可根据实际飞行情况使用训练好的网络预测动作Q值，结合ε-贪婪策略的启发式搜索规则实现动态路径规划，但该方法需提前已知环境信息，对未知环境适应性不强。在无人车路径规划研究中，针对采用多线段规划的路径可能导致的运动速度不连续或过动作等问题，SONG[6]等人采用改进粒子群优化算法与高阶B样条曲线联合方法规划得到曲率连续的无人车平滑路径。刘畅[7]等人采用改进蚁群算法和人工势场法融合，结合空间信息素划分方法，提高复杂地形环境下的月面机器人路径规划成功率和速度。考虑现有路径规划大多针对小区域、局部避障，以及缺少路径安全考虑的问题，于晓强[8]等人结合月面数字高程模型地图，采用改进A*算法提升月面大范围移动月球车全局路径规划能力，通过设计安全启发式函数，提高生成路径的安全性。在导弹路径规划研究中，针对巡航导弹三维航迹规划的复杂性及搜索空间大且效率低的问题，高守玮[9]等人提出一种基于改进蚁群算法的航迹规划方法，引入地形条件与航迹规划的约束条件减小搜索空间，提高三维空间航迹规划效率。针对巡航导弹超低空突防安全路径规划问题，LIU[10]等人基于网格地图方法提出一种新的斜距地图用于路径规划地图描述，采用粒子群优化方法实现多个巡航导弹在水平面内无碰撞路径规划，但该地图描述方法削弱了导弹大范围策略机动时的可用性。针对在Voronoi图规划空间采用传统蚁群算法容易陷入局部最优解的问题，谢春思[11]等人提出一种基于改进蚁群算法的对陆巡航导弹航迹规划方法，通过改进信息素更新方式提高航迹规划算法全局寻优性能。张友安[12]等人将导弹撞击时间和撞击角度控制问题转化为路径规划问题，采用多段相切圆弧连接的三圆弧(Three Circular Arcs，CCC)路径规划方法进行路径调节，可用于在线规划，但该方法无法考虑路径过程中的探测视场角约束。

本文主要研究实现导弹探测效能增强的路径规划方法，为导引头抗干扰探测创造空间优势条件。综上可知，现有路径规划研究主要考虑如何快速到达目标点，未能考虑路径终端进入角度约束问题，无法满足复杂人工诱饵干扰环境下通过路径规划方式提升导弹探测效能的需求，因此还需对导弹抗干扰探测路径规划技术开展进一步研究。

本文主要贡献有两点：1)为实现对目标干扰威胁区域的规避，在规划中运用了多步预测改进A*路径规划算法以提前规避干扰区，减少导弹机动量；2)为实现探测进入角约束下的规划，考虑导弹探测视场角范围约束，提出了动态虚拟目标点替代真实目标点的思路使导弹路径达到期望进入角。

1 A*路径规划方法描述

1.1 问题描述

通常飞机上装备导弹来袭告警系统[13-14]，可对来袭空空导弹进行预警以释放干扰和机动逃逸。这里以空空导弹末段打击敌方飞机目标为例，考虑敌方飞机具有人工诱饵干扰对抗能力，导弹需要在接近目标的过程中规划飞行路径减少干扰遮挡，以增强导引头抗干扰探测效能。由于飞机释放的干扰在空中持续时间有限且存在于特定区域，通常位于目标运动速度方向的后侧且距离目标较近的区域，本文将其描述为干扰威胁区域。当目标释放人工诱饵干扰形成干扰威胁区域时，导弹探测视场内将存在大量干扰目标，需要规划飞行路径避开该区域以更好地探测目标。如图1所示，由于A*路径规划方法具有规划速度快且容易在规划搜索中加入动力学约束以得到可飞行路径，因此本文基于改进A*路径规划方法实现导弹探测效能增强路径规划。

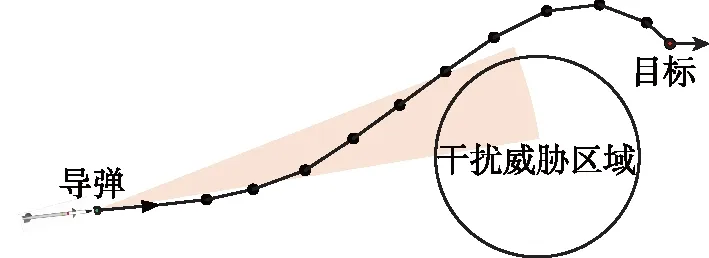
图1 A*路径规划避开干扰区域示意图Fig.1 Schematic diagram of A* path planning for avoiding threat

1.2 导弹质点运动状态描述

在路径规划研究中，通常将运动平台假设为匀速运动质点。定义惯性坐标系Oexeyeze，其中Oexe指向北方，Oeze指向地心，Oeye指向东方。定义运动平台体坐标系Obxbybzb，其中，Obxb轴在其纵向对称平面内指向飞行方向，Obzb轴在其纵向对称平面内指向机体正下方向，Obyb轴垂直于和并指向机体右侧方向。质点三维运动状态更新简化表示如下[15]

(1)

式中，[xPS(k)，yPS(k)，zPS(k)]表示第k时刻的位置；LS(k)表示单步规划距离步长；φ(k)和μ(k)分别表示运动速度的偏航角和倾角，Δφ(k)和Δμ(k)分别表示偏航角增量和倾角增量。

1.3 路径规划约束条件

(1)威胁避障约束

导弹飞行路径要远离目标释放诱饵形成的干扰威胁区域，以降低被干扰的概率。

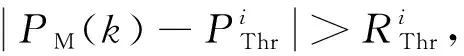
(2)

(2)转弯速率约束

相邻路径线段转向所需的转弯速率不能大于导弹允许最大转弯速率，以保证路径可以被跟踪。

|ωφ(k)|≤ωφmax,|ωμ(k)|≤ωμmax

(3)

式中，ωφmax和ωμmax分别表示允许最大偏航转弯速率和倾角转弯速率。

(3)视场角范围约束

导弹视场角范围θM需要覆盖目标所在位置，以保证可以探测目标。

(4)

式中，φM(k)和μM(k)分别为第k个路径点处导弹速度航向和倾角，φMT(k)和μMT(k)分别为第k个路径点处导弹和目标连线的航向和倾角。探测视场角约束如图2所示。

图2 探测视场角约束Fig.2 Field of view limit

1.4 路径点扩展方式

传统A*算法将路径规划节点扩展方向离散化为多个方向，根据规划步长与转向角度约束计算扩展节点位置[16-17]。图3表示从第k个路径点PM(k)向k+1个路径点PM(k+1)扩展时，以当前速度方向VM(k)为参考，在航向转弯平面和倾角转弯平面上分别有M和N个等间隔扩展方向可选择，其中M和N为奇数，且扩展方向受最大转弯角度αmax和βmax的约束。

图3 路径节点扩展示意图Fig.3 Schematic diagram of path point expansion

1.5 启发式代价函数设计

扩展路径搜索方向的选择通常采用启发式方法进行确定，从而使路径点趋于最优。启发式方法代价函数f(x)包括当前路径点到起始点的路径代价函数h(x)和当前路径点到目标路径点估计函数g(x)两部分，形式如下

f(x)=h(x)+g(x)

(5)

路径代价函数h(x)形式如下

h(x)=w1CT+w2CR+w3CV

(6)

式中，CT，CR，CV分别为威胁代价、转弯代价、探测覆盖代价，w1，w2，w3分别为代价权重系数，各代价函数表达形式如下

(7)

2 A*路径规划方法改进

2.1 基于多步预测的避障规划

在威胁环境下采用传统A*算法的单步扩展方式进行路径规划时，只有在扩展点与威胁区域有碰撞时才会进行转向避障，在无转向角度限制下可以通过增大转向角度来实现，但对于有转向角度限制时可能出现无法避障情况，如图4(a)所示。当采用多步扩展路径节点方式对路径扩展点进行多步预测，可以提前检测到与威胁区域的碰撞，从而可以通过方向选择提前避开威胁区域，如图4(b)所示，多步预测的步数用Ns表示。

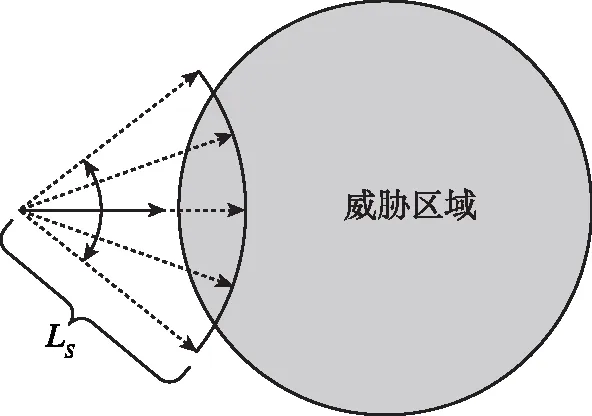
(a)单步扩展路径节点避障

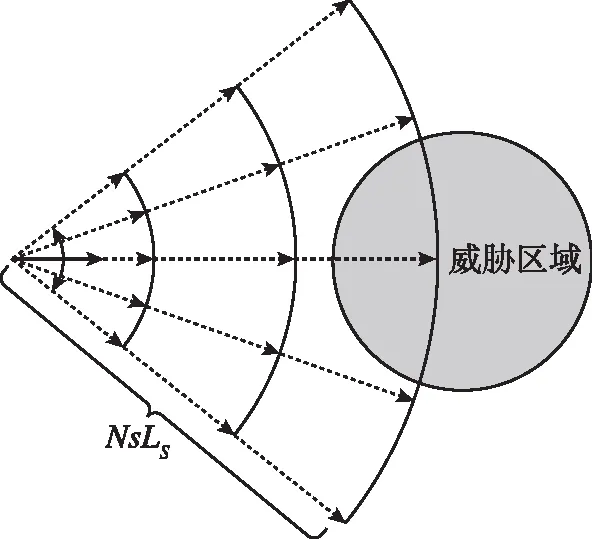
(b)多步扩展路径节点避障图4 单步扩展与多步扩展路径节点避障对比Fig.4 Comparison between one step and multi-step path point expansion

2.2 基于时间步长路径扩展

当前大多数路径规划研究中假定平台运动速度为匀速不变的过程，因此采用固定距离长度作为规划步长。由于空空导弹在不同阶段飞行速度是变化的，因此将路径规划步长改进为速度与时间的乘积，以替换固定距离长度的规划步长。设定好规划时间步长后，在不同速度下规划时只需代入对应速度即可。假定在单次规划周期内导弹速度为恒定值，则步长与转角表示如下

(8)

式中，VS(k)和a分别表示第k时刻的速度、加速度；ΔT表示单步规划时间步长；ωφ(k)和ωμ(k)分别表示偏航转弯速率和倾角转弯速率。假定导弹在规划周期内为恒定速度，其加速度a=0，转弯速率满足约束|ωφ(k)|≤ωφmax，|ωμ(k)|≤ωμmax。

由于路径规划节点扩展采用时间步长进行计算，因此可以将M和N个等间隔扩展方向用相应的转弯角速率来表示，转化关系如下

(9)

2.3 动态虚拟目标点启发方法

现有路径规划研究中较多采用到目标点的距离长度作为节点扩展代价计算依据，导致规划路径方向总是在当前点与目标点连线方向附近进行选择，从而无法调整到达目标点的路径进入角度。为此，本文提出动态虚拟目标点替代真实目标点的思路，使导弹规划路径逐步达到期望进入角度。基于真实目标点处导弹转弯速率约束设计一个与目标点相切的切入圆弧，采用参考点法求解切入圆弧上的动态虚拟目标点。将目标点处进入角方向投影至水平面得到偏航进入角约束，在水平面上求解切入圆弧和动态虚拟目标点，如图5所示。

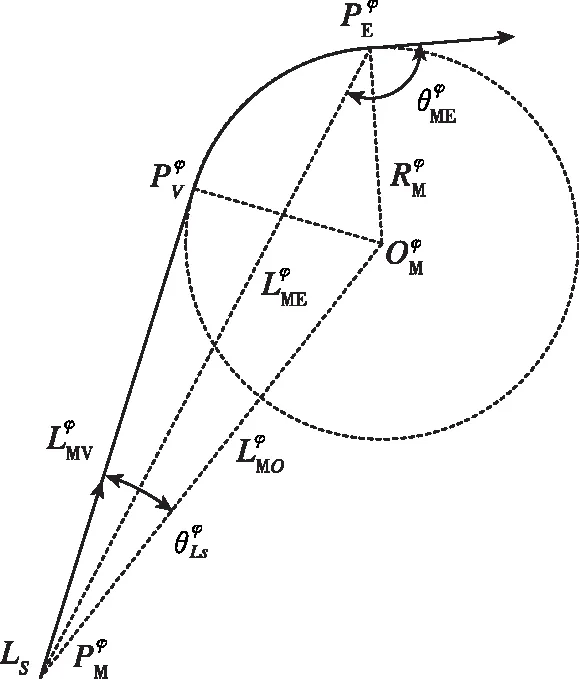
图5 动态虚拟目标点计算原理图Fig.5 The dynamic virtue target point compute method

(10)

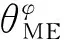
根据导弹当前规划路径点和切入圆弧圆心相对距离，结合参考点法，采用公式(11)～(14)计算动态虚拟目标点的位置PVx和PVy，公式如下

(11)

(12)

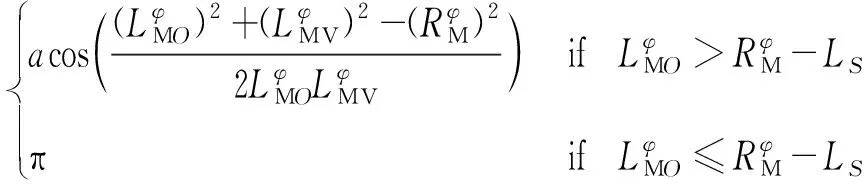
(13)

(14)

2.4 带进入角的路径规划算法流程

带进入角的路径规划算法流程如下。

步骤1：初始化参数，设定路径规划起点和终点参数、路径规划参数、路径规划约束条件、环境威胁参数。

步骤3：最优路径扩展点循环搜索。令最优代价值Cbest=1。

步骤3.1：采用公式(11)～(14)计算动态虚拟目标点PV。

步骤3.2：判断是否有扩展方向可选择。从M×N个扩展方向中依次选择一个扩展方向(m，n)，如果有方向可选，则进入下一步；如果所有方向已选择完，则进入步骤4。

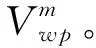
步骤4：判断结束规划的条件。

步骤4.1：判断是否达到最大航点数。判断当前已规划路径点个数kWP是否大于最大路径点数量NWP。如果满足条件，则转步骤4.2；如果不满足条件，则转步骤5。

3 仿真试验及结果分析

3.1 仿真参数设置

为验证本文提出的考虑路径终端进入角度约束的探测效能增强路径规划方法的规划效果，首先对比分析单步预测扩展路径与多步预测扩展路径两种方式的路径规划结果所实现的干扰威胁区规避效果，再对比分析无终点进入角度与不同终点进入角度的路径规划结果所实现的探测效能增强效果。

导弹及路径规划参数如表1所示。

表1 导弹及路径规划参数Tab.1 Missile and path planning parameters

目标释放的诱饵干扰可假设为以目标位置为顶点的锥形区域。为便于表示干扰区域，本文用位置和半径均不同的两个圆形区域来表示，参数如表2所示。

表2 目标及威胁区参数Tab.2 Target and threat area parameters

3.2 仿真结果及分析

如图6所示仿真结果表明，单步预测扩展方式路径规划存在无法避开干扰威胁区域的情况，多步预测扩展方式路径规划可以绕过干扰威胁区域，预测步数越多，得到的规划路径最大曲率越小且长度越短。由于单步预测扩展方式只向前检测一步扩展的规避干扰威胁区域情况，在规划路径到达干扰威胁区域附近时才能判断是否需要转向以避开干扰威胁区域，此时需要较大的转弯速率才能实现避开干扰威胁区域，超出了导弹最大转弯能力，因此停止继续路径规划。两步预测扩展方式得到的规划路径虽然避开了干扰威胁区域，但由于其在避开干扰威胁区域时路径方向偏转时间较晚且角度较大，导致后续以最大转弯能力也无法规划至目标点位置。三步、四步、五步预测扩展方式均得到了较好的规划路径并避开干扰威胁区域，预测扩展步数越多路径曲率变化越平缓。

图6 不同扩展步数的路径规划结果对比Fig.6 Path planning comparison of different steps of expansion

如表3所示不同扩展步数的路径规划结果统计，除单步预测扩展方式规划路径提前终止只得到13个路径点、4.8km路径长度、303ms耗时外，随着多步预测步数的增加，规划得到的路径点数量逐渐变少，路径长度变得更短，但消耗时间变得更长。

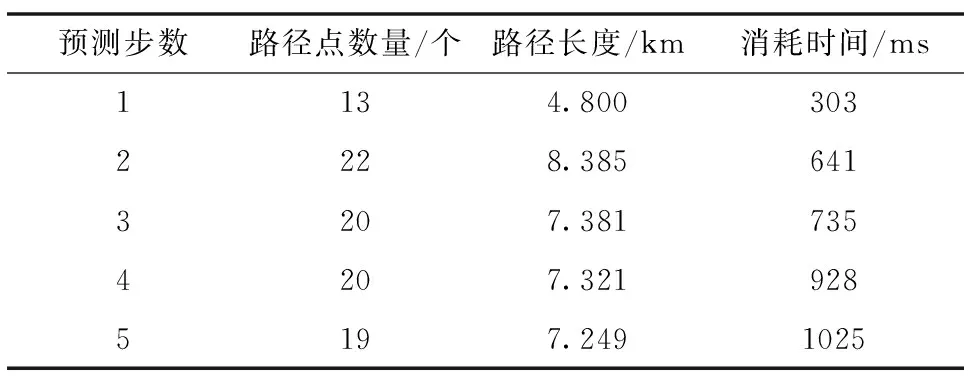
表3 不同扩展步数的路径规划结果统计Tab.3 Path planning result statistics of different steps of expansion

如图7所示不同进入角路径规划结果对比，图中以x轴方向为参考，给出150°，160°，170°，180°四种不同进入角度的规划路径以及无进入角的规划路径，均采用三步预测扩展方式进行路径规划。无进入角路径规划方法在导弹、目标、干扰威胁区域等参数固定的情况下得到的路径固定，与无进入角路径规划相比，带进入角路径规划可设置不同进入角度从而得到不同的路径规划结果，满足不同进入角度探测需求。在图7中所示弹目状态下，无进入角规划路径存在两次转弯机动，而有进入角规划路径只有一次转弯机动，随着进入角度的增加，规划路径曲率逐渐变得更平缓，即导弹飞行所需最大机动减小。

图7 不同进入角路径规划结果对比Fig.7 Path planning comparison of different entry angle

如表4所示，不同进入角度路径规划结果统计，随着进入角度的增加路径规划点数量和路径总长度均会变化，最大路径点数量21个、最长路径长度7.823km，最少路径点数量19个、最短路径长度7.228km；无进入角度规划的路径比较固定，路径点数量20个、路径长度7.381km；定义探测覆盖时长占比为可探测路径点数量与总路径点数量比值，其中可探测路径点采用规划的路径点与终点连线不经过干扰威胁区的方式选择；探测覆盖时长占比从0.4286变化为0.2105，而无进入角度规划的路径探测覆盖时长占比为0.2，表明有进入角度规划方法可以提高对目标的覆盖时长占比，有利于导引头持续捕获目标以增强探测效能。

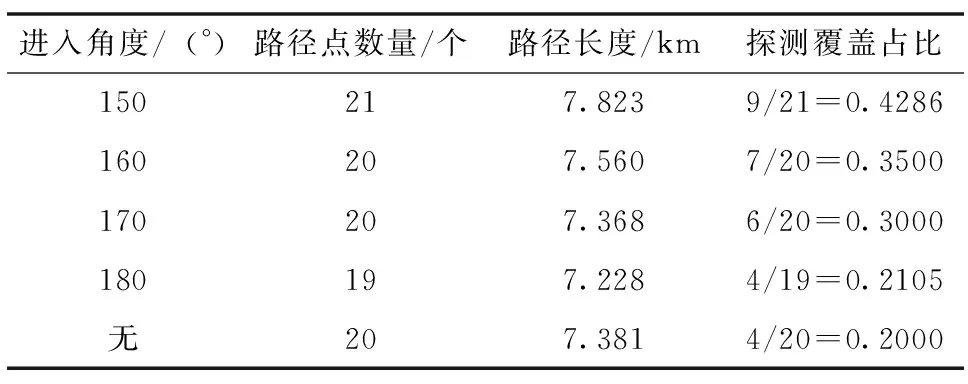
表4 不同进入角度路径规划结果统计Tab.4 Path planning result statistics of different entry angle

4 结 论

本文针对空空导弹在拦截飞机目标时规避人工诱饵干扰的探测路径规划需求，在传统A*路径规划方法的基础上进行了改进，实现了面向探测效能增强的导弹路径规划，主要贡献有：

1)采用单步预测扩展方式路径规划存在无法绕过干扰威胁区域的情况，而多步预测扩展方式路径规划可以绕过干扰威胁区域，且随着预测步数越多，得到的规划路径最大曲率越小且长度越短，但预测步数过多会带来规划耗时增加，因此实际使用中需要进行权衡选择；

2)采用有进入角度规划方法可以减少导弹机动次数并提高对目标的覆盖时长占比，能有效避开干扰威胁区域以增加持续探测时间，有利于导引头持续捕获目标以增强探测效能。