导弹球窝喷管电动伺服系统摩擦积分自适应补偿控制*
庞 博,潘卫东,王厚浩,唐德佳,周 道
(1. 海装上海局驻上海地区第六军事代表室·上海·201111;2. 上海航天控制技术研究所·上海·201109)
0 引 言
摆动喷管作为导弹推力矢量系统的重要执行部分,一般采用两路正交分布的伺服系统驱动实现摆角的作动,伺服系统将喷管摆角指令解算为伺服机构线位移量,并通过内部伺服算法驱动伺服机构工作,进而实现喷管摆角操纵[1-2]。摆动喷管按接头结构形式可分为球窝喷管及柔性喷管,其中球窝喷管以其摆心漂移量小、驱动力矩小等优点,正逐渐在导弹发动机推力矢量系统中得到广泛的应用[3]。
与以弹性力矩为主要负载成分的柔性喷管不同,球窝喷管由于接头为阴、阳球面配合,其负载特性主要表现为典型的非线性摩擦负载力矩以及少量弹性力矩[4]。球窝喷管电动伺服系统低速工作时由于受球窝喷管固有非线性摩擦力影响,在运动过程中易产生爬行、波形畸变等现象[5],大大降低了球窝喷管低速稳态跟踪性能,严重时会导致系统产生极限环振荡。针对摩擦非线性问题,主要有基于摩擦模型与不基于摩擦模型等解决方法,其中不基于模型主要有自抗扰控制(Active Disturbance Rejection Control,ADRC)、扰动观测器(Disturbance Observer,DOB)等策略[5-6],基于模型的摩擦抑制研究相对较多,Zhou[7]等人针对光电伺服平台中摩擦,建立了含Lugre摩擦模型的系统模型,并设计了一种新的有限时间鲁棒自适应非奇异快速终端滑模控制来保证系统在非线性干扰下的稳定性;李俊阳[8]等人为提高机器人关节稳态跟踪精度,引入改进Lugre摩擦模型,采用自适应算法实现摩擦补偿,并引入反步设计保证系统稳定性,通过仿真验证了算法的可行性;Wang[9]等人采用连续摩擦模型来描述伺服机构的摩擦动力学,通过自适应律对包括摩擦模型在内的未知系统参数进行在线估计,引入辅助滤波器来提取估计误差,并设计积分鲁棒控制器,保证系统严格稳定。文献[10-13]等采用改进Lugre摩擦模型设计伺服系统非线性摩擦自适应控制器,并通过了仿真及试验验证,均取得了较好的效果。
为提高导弹球窝喷管电动伺服系统低速跟踪精度,针对导弹球窝喷管电动伺服系统存在摩擦非线性问题,建立含稳态改进Lugre摩擦模型的系统非线性模型,并引入可变参数描述摩擦参数的变化;基于反步设计方法,通过递推Lyapunov函数完成摩擦积分自适应补偿控制器(Friction Integral Adaptive Compensation Controller,FIACC)设计并分析其稳定性;采用遗传算法实现球窝喷管稳态Lugre摩擦模型参数辨识;最终,通过仿真试验验证算法的可行性及有效性。
1 系统非线性模型
球窝喷管矢量系统简图如图1所示。球窝喷管一般采用两路正交分布的伺服系统驱动实现摆角的作动,进而控制导弹俯仰、偏航两方向姿态控制,伺服系统通过接收弹上计算机指令作动,为典型的位置伺服系统。
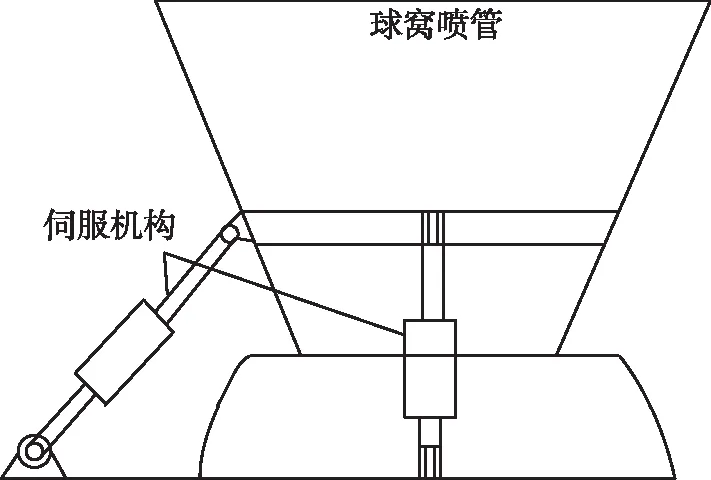
图1 球窝喷管系统简图Fig.1 Ball-socket nozzle system diagram
1.1 伺服系统模型
伺服系统采用表贴式永磁同步电机驱动,电机阻尼一般为极小值,建模时简化为0,给出永磁同步电机电气模型如下
(1)
式中,ud、uq、id、iq分别为直、交轴电压和电流分量,ψf、Ls、Rm分别为永磁同步电机磁链、电感及相电阻,P为电机极对数,ω为电机机械转速。采用id=0矢量控制策略,稳态工作时,有
uq=Rmiq+Pωψf
(2)
建立简化后电动伺服系统控制框图如图2所示。
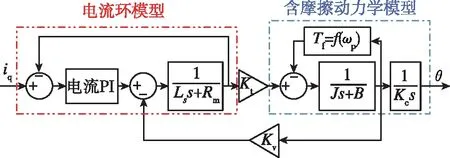
图2 电动伺服系统简化控制框图Fig.2 Simplified control block diagram of electric servo system
图2中,Kv为反电动势系数,f(ωp)为摩擦力函数,如图2所示,q轴电流环可等效为一阶惯性模型,可简化为常系数,则有稳态下含摩擦力伺服系统动力学方程(忽略惯性力矩)
(3)
式中,ωp为喷管操纵速度,Tf为摩擦力矩,J为折算至电机转动惯量,Kt为电机转矩系数,Kc为系统传动比。
1.2 摩擦模型表述
采用Lugre摩擦模型对摩擦力进行表述,该模型考虑了摩擦的静态特性(静摩擦、库仑摩擦、黏滞摩擦等),还体现了摩擦的动态特性,例如摩擦的突变、停止-滑动等现象[12]。Lugre摩擦模型表述如下所示
(4)
式中,Ts,Tc分别为静摩擦力矩、库仑摩擦力矩,ωp为物体表面相对运动速度,ωs为Stribeck切换速度,z为接触面鬃毛变形量,σ0为鬃毛刚度系数,σ1为鬃毛阻尼系数,σ2为黏性摩擦系数,g(ωp)严格正实数且有界。
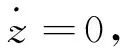
z=sgn(ωp)g(ωp)
(5)
综合式(4)、(5),简化后Lugre摩擦模型可表述为
Tf=Tcsgn(ωp)+(Ts-
(6)
2 摩擦积分自适应补偿控制器设计
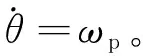
Tf=αTcsgn(ωp)+(βTs-
(7)
将式(7)代入式(3)可得
(8)
式中,θ为喷管摆角,其中α∈[0,1],β∈[0,1],γ∈[0,1]。
针对上式,采用非线性反步计算方法,设计含可变摩擦参数自适应补偿喷管角度跟踪控制器。
定义球窝喷管摆角位置跟踪误差量为
e1=θr-θ
(9)
式中,e1为喷管角度跟踪误差,θr为喷管期望摆角。误差微分为
(10)
选择如下Lyapunov函数
(11)
(12)
将式(10)代入式(12)可得
(13)
设计中间环节控制输入量θ1d如下
(14)
式中,k1,k2分别为可调节正实数。中间环节控制输入与喷管速度误差量如下
(15)
求导可得
(16)
将式(8)代入式(16)中可得
(17)
(18)
针对系统跟踪误差e2及参数估计误差,定义系统Lyapunov函数如下
(19)
式中,k3为可调节正实数,λ1、λ2、λ3为自适应增益,V2求导可得
(20)

(21)
则有
(22)
式中,由于α,β,γ为缓变量,因此将式(18)代入式(22),可含估计参数式得
(23)
(24)
式中,k4为正实数。
将式(24)代入式(23)可得
(25)
(26)
含摩擦积分自适应补偿控制器电动伺服控制系统框图如图3所示。
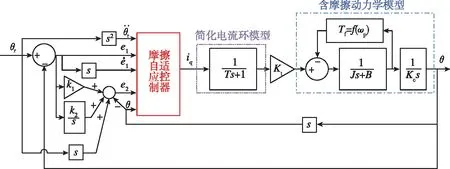
图3 摩擦自适应积分控制框图Fig.3 Block diagram of friction integral adaptive control
3 摩擦参数辨识
依据式(6)可知,需辨识参数有Ts,Tc,ωs及σ2等;试验时,可给定伺服系统多组恒速指令,并记录喷管稳定运行时力矩传感器数值。
为获取更精确试验统计参数,采用遗传算法对待辨识参数向量W=[Ts,Tc,ωs,σ2],定义辨识误差
e(W,ωi)=Ti-Tss(W,ωi)
(27)
式中,ωi为第i次试验时速度,Ti为第i次试验测试摩擦力,Tss(W,ωi)为预估摩擦力。设计误差目标函数为
(28)
辨识应使Δ→0,取个体自适应函数有
f(Xk)=Δ(Xk),k=1,2,…,N
(29)
式中,Xk为个体,N为种群大小。选择操作方式为随机采样,变异操作采用高斯算子,用均匀交叉算子进行交叉操作,种群大小N取200,迭代次数T取1000,变异概率取0.02,交叉概率取0.95。辨识参数如表1所示。

表1 摩擦辨识参数表Tab.1 Table of friction identification parameters
4 仿真试验
搭建含摩擦模型的永磁同步电机驱动电动伺服系统仿真模型,并完成控制器设计。电机仿真参数如表2所示。

表2 电机仿真参数Tab.2 Motor simulation parameters
电流环增益kp、积分参数ki、控制周期T分别为1.2,100,0.0001s。控制器参数设计如表3所示。

表3 控制器参数Tab.3 Controller parameters
4.1 慢正弦跟踪仿真
给定电动伺服系统幅值为1°,频率为0.1Hz慢正弦指令跟踪信号,观察电动伺服系统反馈角度曲线跟踪情况。为验证所设计控制算法有效性,设计两组对比试验如下。
1)方案一:传统PID控制;
2)方案二:摩擦积分自适应补偿控制(简称FIACC控制)。
慢正弦跟踪对比仿真试验结果如图4所示。

(a)对比跟踪曲线图
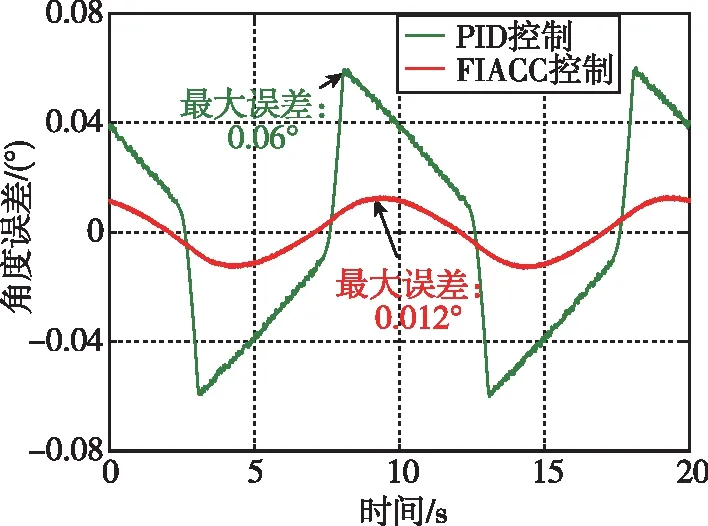
(b)跟踪误差对比图图4 慢正弦跟踪对比结果图Fig.4 Comparison results of slow sine tracking
从图4中可知,电动伺服系统跟踪幅值为1°,频率为0.1Hz慢正弦指令时,采用传统PID控制在正弦波峰处出现波形畸变(平顶)现象,且在低速换向起步时相位滞后明显,跟踪曲线最大误差达0.06°,而采用本文提出的摩擦积分自适应补偿控制时,波形畸变被明显抑制,且相位滞后减小,跟踪曲线最大误差为0.012°,精度提高了约80%。该控制器能够较好抑制摩擦对电动伺服系统影响,提高球窝喷管电动伺服系统跟踪精度。
4.2 斜坡跟踪仿真
给定电动伺服系统幅值从0°增加至7°,斜率为0.1(°)/s指令信号,仿真试验时,同样设计如4.1节所述两组对比试验。
斜坡跟踪仿真试验结果如图5所示。
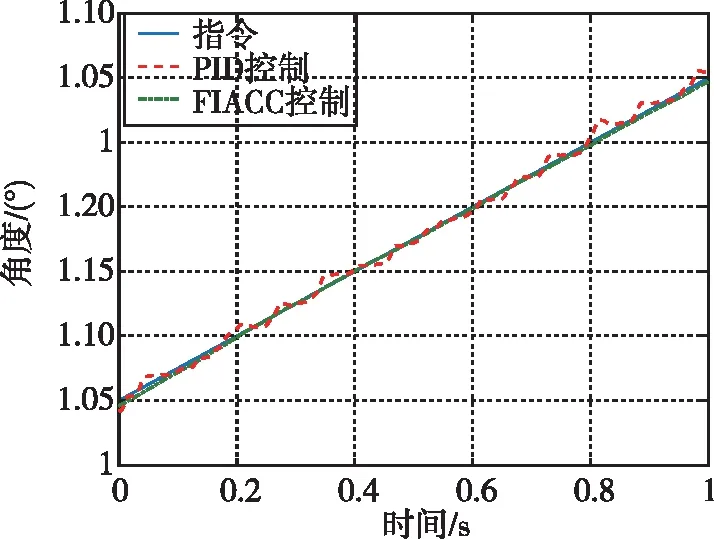
图5 斜坡跟踪对比结果图Fig.5 Comparison results of skew wave tracking
从图5中可知,给定电动伺服系统幅值从0°~7°,斜率为0.1(°)/s的指令信号时,采用PID控制出现跟踪曲线爬行现象,伺服系统在“停止-运动”状态间切换,跟踪误差最大为0.02°,而采用摩擦积分自适应补偿控制后,角度跟踪曲线趋于平稳,摩擦造成的爬行现象被抑制,此时最大误差为0.005°,跟踪精度明显提升。
5 结 论
针对球窝喷管电动伺服系统中存在摩擦非线性的问题,提出一种基于Lugre摩擦模型的摩擦积分自适应控制策略。考虑球窝喷管摩擦随发动机压力、温度变化等因素,建立了含可变参数稳态Lugre摩擦模型的电动伺服系统动力学方程,采用反步法设计摩擦积分补偿非线性控制器,并引入自适应参数进一步提高补偿精度。基于Lyapunov函数完成所设计控制器稳定性证明。采用遗传算法实现摩擦基本参数的辨识,并完成含摩擦非线性电动伺服系统建模,最终,通过仿真验证试验的结果表明,相比PID控制,本文所提出非线性控制器能较好抑制球窝喷管电动伺服系统低速运行时的波形畸变,提高了球窝喷管跟踪精度。

