和若铁路预制装配式桥墩优化设计研究

张 军，徐 镭，李一鸣，于 博

（1.兰州交通大学土木工程学院，甘肃 兰州 730070；2.中铁二十一局集团第一工程有限公司，新疆 乌鲁木齐 830063）

0 引言

在土木工程领域大发展的背景下，我国开始对预制装配式结构有了更高的重视，不仅应用于成熟的房屋建筑，还应用在较为成熟的桥梁上部结构和隧道中，同时向桥梁下部结构预拼装阶段发展，以改变现有桥梁施工方式。与传统桥梁设计施工方式相比，这种预拼装方式能减少对环境的污染、节省工期、减少不必要的浪费、改善施工过程且能保证工程质量。

基于预制装配式结构，国内外开展了相关研究。如美国新泽西州的胜利桥[1]，美国德克萨斯州183 高架桥，2002 年建成的SH 66 over Lake Ray Hubbard桥盖梁与墩身间采取了钢筋和波纹管连接技术，美国佐治亚州Interstate 85 interchange 桥整体采用预制拼装技术，美国华盛顿州I-5 Grand Mount to Maytown I/C 两跨径预制梁桥于2011 年完工，预制构件间通过金属波纹管连接构造形成整体。我国在20 世纪90 年代初期开始研究预制装配化墩柱，在2002 年修建的东海大桥，除岛墩为现场浇筑外，其余均为预制装配式桥墩[2]；杭州湾跨海大桥中的引桥大部分采取的是预制装配化墩柱[3]；上海长江大桥中部分跨径桥墩应用了预制装配构造技术[4]；浙江舟山金堂大桥中非通航孔跨间桥墩采用预制拼装式墩柱，从而提高了施工速度[5]。

随着预制构件在装配化设计与施工技术方面的大力推广，已开展大部分有关预应力钢束连接构造、墩型形式选择等的预制拼装桥墩[6-12]。

1 工程概况

新建一铁路，线路总长825.5 km。桥梁全长88.9 km，占线路总长的10.5%，全线墩柱均不高，墩高小于10 m 的桥墩占70%。路基全长736.6 km，占线路总长的89.5%。全线地质以粉砂、细砂、细圆砾土、粗圆砾土、卵石土为主。全线地震动峰值加速度值为0.05～0.15g，地震动反应谱特征周期为0.40～0.45 s。具体工程实际背景见图1，线路标准见表1。

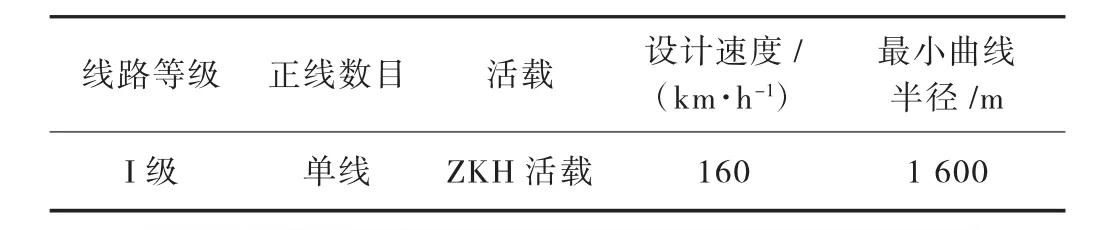
表1 线路标准

图1 新建铁路

2 总体概述

2.1 构件设计

本文以（24×24）m 等跨梁段直线预制拼装桥墩为设计依据，在此基础上进行相关项目优化，图2 为盖梁整体构造图，图3 为桥墩整体构造图。

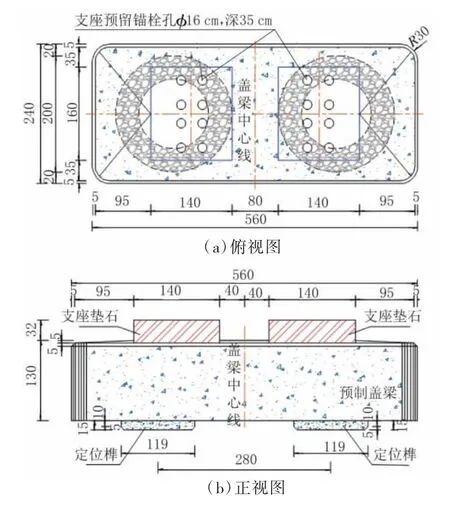
图2 盖梁整体构造图（单位：cm）

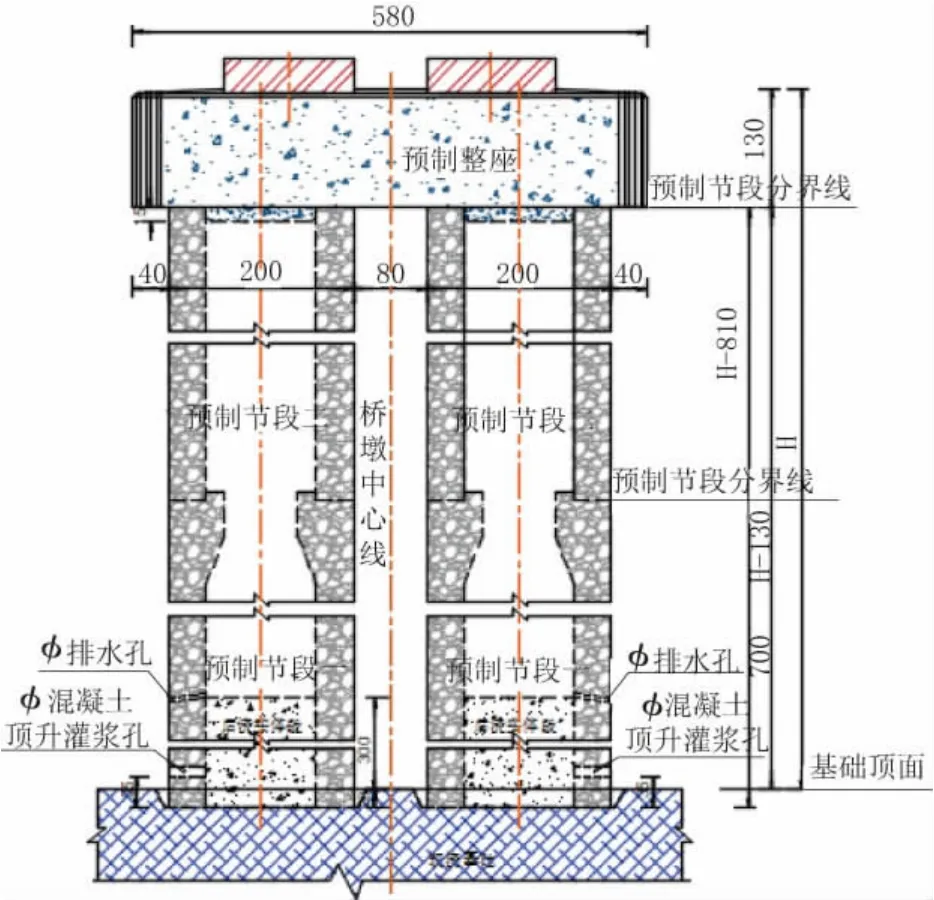
图3 桥墩整体构造图（单位：cm）

预制装配式墩身分为一至二，两个节段，墩身直径2 m，壁厚40 cm。现浇杯形基础、墩身节段、盖梁间通过采用预应力束连接为整体结构，在预制节段分界面处涂抹环氧树脂胶，进行密封性及可靠性连接处理。预应力锚固端应设置在现浇基础内，采用PM15-12 型锚具，张拉端设置在盖梁顶部，并预留左右各6 孔张拉槽口及支座锚栓孔，采用DSM15-12型锚具，基础预留深度160 cm 锚穴。盖梁底部与墩身对应位置处设置高15 cm，直径119 cm 的圆形锚固定位榫。

2.2 构件材料

盖梁、墩身均采用C50 混凝土，现浇杯形基础采用C40 混凝土；预应力束采用符合《预应力混凝土用钢绞线》（GB/T 5224—2014）标准的φs15.2 mm 高强低松弛钢绞线； 盖梁采用φ25、φ20、φ16、φ12 HRB400 级及10 HPB300 级钢筋，配筋率为6.9%，墩身采用φ12 HRB400 级及φ10 HPB300 级钢筋，配筋率为4.0%（按照一个桥墩计算）。

2.3 荷载计算

主梁自重为189.7 t，二期恒载为78.83 kN/m，则作用在单个桥墩上部结构恒载为3788.92 kN。列车活载采用ZKH 活载，动力系数采用最新《铁路桥涵设计规范》（TB 1002—2017）相关规定进行计算，得出列车制动力为304.51 kN。

3 固端边界干扰局部应力

通过空心墩构造看，墩身、盖梁及承台连接部位，相当于固端的边界条件，对墩壁变形起着约束作用，因而产生局部的纵向应力和环向应力，称为边界干扰局部应力[13]。假设将圆环空心墩视为受中心压力P 作用的圆柱壳，端部变形和约束情况见图4。

图4 中心受压下圆柱形空心墩端部变形约束情况

中心受压单位宽墩壁承受均匀轴向压力和压应力为：

式中：P 为墩柱中心压力；R 为固端转动半径；d 为墩柱壁厚。

在压应力作用下，如果顶帽墩壁变形无约束，则墩壁会产生向外的均匀自由扩张变形，其值为：

式中：ε0为墩壁环向应变；εy为墩壁纵向应变；ν 为混凝土的泊松系数，可取1/6；E 为混凝土弹性模量；Ny、σy含义同式（1）和（2）所述。

在实际中，盖梁和承台及墩身为固结，要约束墩壁向外变形，同时还需保持转角为零，应在墩身端部作用着均匀的径向附加剪力H0和M0弯矩，使端部产生相反的位移为：

从而使径向变位ω 和θ 角变位都为零。

基于圆柱形薄壳结构在边界均匀荷载H0和M0作用下壳体的变位和内力公式，根据转角为零的边界条件，可推导出H0与M0之间的关系式：

圆柱壳体在端部均匀荷载H0和M0作用下的径向变形和内力计算公式为：

式中：ω 为径向位移，向外为正；My为墩壁所受单位宽度上的弯矩，外侧受压为正；Mφ为墩壁所受单位宽度上的环向轴力，拉正压负；其他符号含义同式（1）、式（2）、式（3）及式（5）的解释一致。

再根据边界条件y=0，ω= Δ～=-Δ=-Pν Ny/（Ed），由式（6）可得

将式（9）带入到式（7）和式（8）中可得中心受压作用下，固端干扰产生的单位宽度附加纵向弯矩、环向弯矩和环向轴力为：

由此产生的纵向和环向局部应力，可按照高度d为d 的单位宽矩形板进行计算：

由式（13）和式（14）可以看出，纵向局部应力与纵向局部弯矩有关，My按负指数振动函数变化，衰减很快。Nφ和Mφ与环向局部应力有关，距离端部一定位置处会产生环向拉应力。

4 优化设计

4.1 墩柱壁厚优化设计

本文结合实际墩柱外径为2 m，墩高为12 m，外径、墩高始终保持不变，改变墩柱壁厚，选取b 为35 cm、40 cm、45 cm、50 cm 四种不同壁厚形式（见表2），利用MIDAS CIVIL 有限元进行上部结构重力、列车制动力等主要荷载工况的施加，根据各控制点处内力、位移数值对比分析其力学性能、结构安全性及稳定性影响。

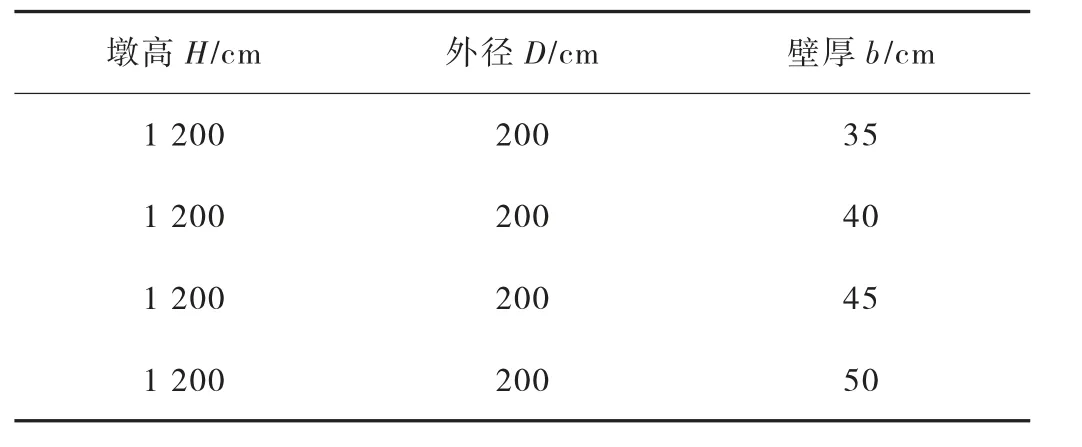
表2 墩柱壁厚设置

4.2 预应力束数优化设计

本文设置预应力束束数为n=10，12，14，16 束四种情况，基于MIDAS CIVIL 有限元分析软件，将上部结构自重、列车制动力等主要荷载工况施加到盖梁顶部，根据各控制点处内力、位移数值对比分析其力学性能、结构安全性及稳定性影响。预应力束的张拉力为1264.98 MPa，现已增减墩柱预应力束束数，保持张拉力不变，见表3。

表3 预应力束数设置

4.3 后浇段优化设计

本文结合实际墩柱外径为2 m，墩高为12 m，外径、墩高始终保持不变，仅改变墩柱后浇段高度，选取后浇段为h=2.0，3.0，3.2，4.0 m 四种不同高度（见表4），基于MIDAS CIVIL 有限元分析软件，将上部结构自重、列车制动力等主要荷载工况施加到盖梁顶部，根据各控制点处内力、位移数值对比分析其力学性能、结构安全性及稳定性影响。

表4 后浇段高度设置

5 结构分析

本文选取MIDAS CIVIL 有限元模拟软件作为桥墩结构建模工具，桥墩模型每10 cm 建立一个节点，重要位置对节点进行细分，整个双柱式空心墩共建立节点251 个，建立单元246 个。

桥墩承台顶设置了后浇实体段，采用C55 微膨胀混凝土浇筑，并预留后浇段连接钢筋，通过墩柱、承台与后浇段三者形成固结，达到整体受力作用，从而提高结构稳定性和耐久性。

5.1 墩柱壁厚优化分析

对墩柱壁厚分别为b 为35、40、45、50 cm 的桥墩进行MIDAS 有限元模拟分析，此时保持预应力束数为12、外径2 m、后浇段高度为3.2 m 三项参数不变，应得出整体桥墩模拟结果，见图5 所示。桥墩设置四种不同壁厚经MIDAS 有限元分析得出最大内力和位移运算结果汇总见表5。

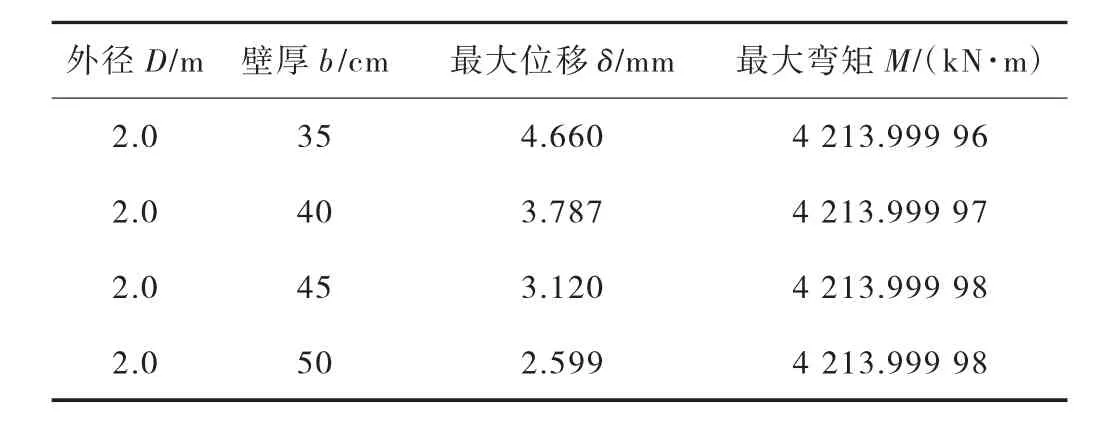
表5 桥墩不同壁厚指标运算结果汇总

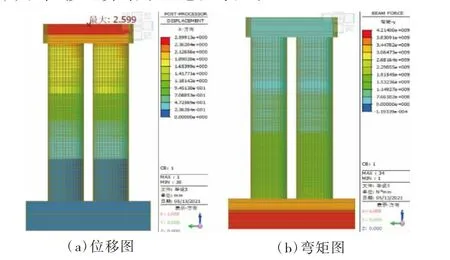
图5 桥墩50 cm 壁厚模拟结果

通过对表5 及图6 分析结果发现：将桥墩壁厚降低后，其承受上部荷载产生的墩顶位移有所增加，相比40 cm 原尺寸位移增加较快。桥墩壁厚设为50 cm 时，其承受上部荷载产生的墩顶位移降低明显，相比40 cm 原尺寸位移降低31.37%。桥墩产生的最大弯矩随壁厚增加而增大，但增加幅度不大对桥墩受力情况并没有较大影响。可见50 cm 壁厚设计的桥墩可以满足和若铁路实际工程项目的设计要求，较为合理。

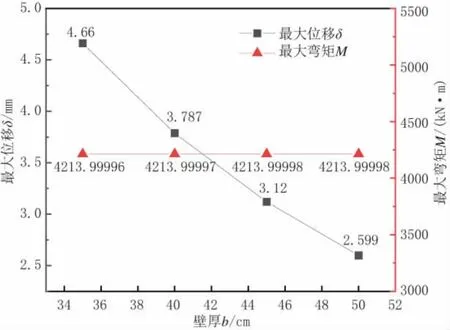
图6 壁厚变化对弯矩及位移影响结果对比

5.2 预应力束数优化分析

对墩柱预应力束数分别为n=10，12，14，16 束的桥墩进行MIDAS 有限元模拟分析，此时保持壁厚40 cm、外径2 m、后浇段高度为3.2 m，三项参数不变，得出整体桥墩模拟结果，见图7 所示。桥墩设置四种不同预应力束经MIDAS 有限元分析得出最大内力和位移运算结果汇总见表6。

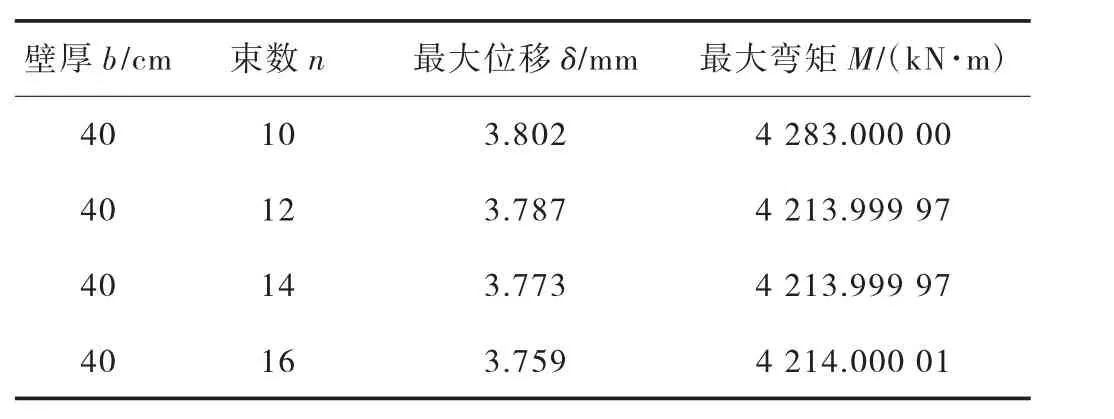
表6 桥墩不同预应力束数指标运算结果汇总

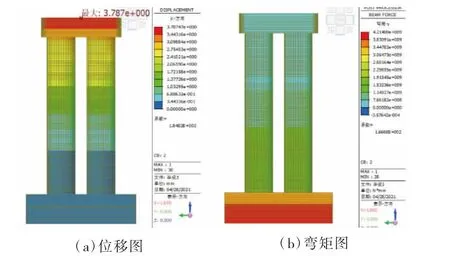
图7 12 束预应力筋模拟结果

通过对表6 及图8 分析结果发现：将桥墩预应力束数增加后，其承受上部荷载产生的墩顶位移有明显减小。当预应力束设为10 时，与12 束相比最大水平位移增加了0.39%，预应力束为14 时，其最大水平位移降低0.37%，足以满足和若铁路的设计要求。桥墩产生的最大弯矩随束数增加而减小，但减小幅度不明显，对桥墩并不造成任何影响。可见12 束预应力设计的桥墩可以满足和若铁路实际工程项目的设计需求，较为合理。

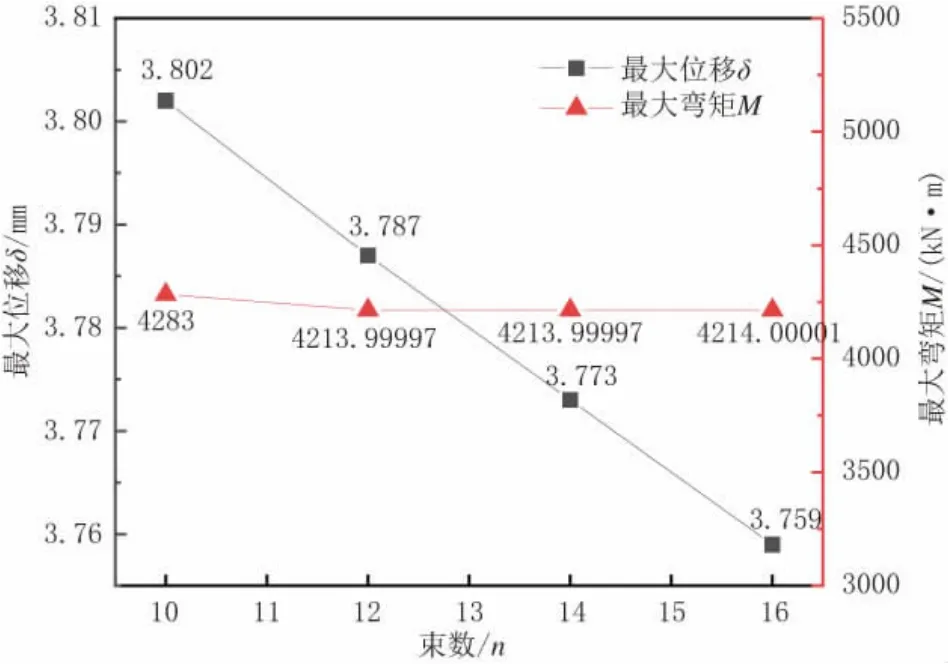
图8 预应力束数变化对弯矩及位移影响结果对比

5.3 后浇段高度优化分析

本文对墩柱后浇段高度分别为h=2，3，3.2，4 m的桥墩进行MIDAS 有限元模拟分析，此时保持壁厚40 cm、外径2 m 两项参数不变，得出整体桥墩模拟结果，见图9 所示。桥墩设置四种不同后浇段高度经MIDAS 有限元分析得出最大内力和位移运算结果汇总见表7。

表7 桥墩不同后浇段高度指标运算结果汇总

图9 4 m 后浇段高度模拟结果

通过对表7 及图10 分析结果发现：将桥墩后浇段高度增加后，其承受上部荷载产生的墩顶位移有所减小。当后浇段高设为2 m 时，较原结构高度3.2 m相比最大水平位移增加了2.03%；当后浇段高为4 m时，其最大水平位移降低1.61%，足以满足和若铁路的设计要求。桥墩产生的最大弯矩随后浇段高度增加而减小，但减小幅度较小，对桥墩并不造成任何影响。可见后浇段高度为4 m 的桥墩可以满足和若铁路实际工程项目的设计需求，较为合理。

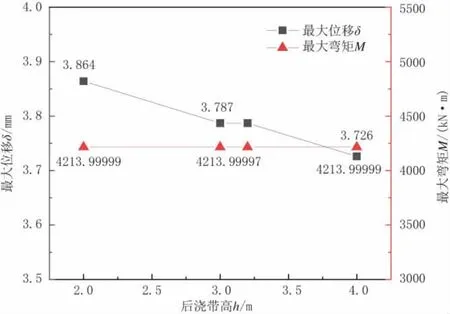
图10 后浇段高度变化对弯矩及位移影响结果对比

6 结语

通过对和若铁路预制装配式桥墩在墩柱壁厚、预应力束数及后浇段高度三者在单因素影响下的优化设计研究及固端边界干扰局部应力影响，基于MIDAS CIVIL 有限元模拟分析最终得出以下结论：

（1）桥墩壁厚发生改变时，能不同程度影响其力学性能，并且影响程度在设计允许范围内。设计壁厚为45 cm 时能够更好满足实际工程的设计需求，也能获得更大的安全性和稳定性。

（2）预应力束数变化时，对于桥墩力学性能并没有较大影响，预应力束数按12 根设计时能满足桥墩构造设计更经济合理。

（3）桥墩后浇段高度改变时，承受同一荷载后对整个桥墩的力学性能提升较低。后浇段高度为4m 时能更好满足实际工程的设计需求，保证了结构既经济合理又安全可靠。