三峡库区巴东水文站蒸发模型研究

王玉涛,付 鑫,吕超楠,伍 勇

(1.长江水利委员会水文局 长江三峡水文水资源勘测局,湖北 宜昌 443000; 2中国长江三峡集团有限公司,湖北 宜昌 443000)

0 引 言

水面蒸发是自然界水循环中最基本的因素之一,也是水库、湖泊等自然水体水量损失的主要原因。中国新疆北部平原区大型水库年蒸发损失可占水库总蓄水量的40%[1]。因此,水面蒸发的科学估算一直是水文学和气候学研究的重点之一[2]。

水面蒸发过程受各种条件(如气象、土壤、植被等)的影响,在自然条件下获得蒸发量的绝对数值较为不易。因此,基于气象要素的水体蒸发估算方法在实际应用中较广泛,利用气象要素计算蒸发的模型研究较多,目前常用的水面蒸发模型主要有彭曼模型、质量转移模型和道尔顿模型[3-5]。彭曼模型需要使用水面辐射平衡资料,而中国观测太阳辐射的站点很少,观测水面辐射平衡的站点更少,使彭曼模型的应用受到很大限制。质量转移模型的结构简单,在欧美许多国家普遍使用,但在中国的使用效果较差,主要原因在于该模型中E/Δe-W(E为蒸发量,Δe为饱和水汽压差,W为风速) 关系的模拟采用了最简单的正比例函数,不符合中国气候特点。道尔顿模型的结构也较简单,在中国各地应用广泛,但由于水面蒸发对微地形、微气象条件的影响非常敏感,加上近地面空气水平平流对蒸发器测蒸发量及其与气象因素关系的影响突出,造成水面蒸发经验公式具有很强的局地性特征。因此正确认识水面蒸发量与气象因子之间的关系,建立区域性的水面蒸发计算公式,对于水库水面蒸发的模型研究具有重要作用[6-7]。

本文分析三峡库区巴东水文站水面蒸发及气象数据,基于灰色关联度和偏相关系数分析蒸发与气象因子(气温、水汽压、蒸发池内水温、风速、日照等)的相关度,采用5种不同的蒸发模型(通用公式、李万义修正模型、回归模型、BP和ELM 神经网络)定量解析不同气象要素对蒸发趋势的贡献,分析了不同蒸发模型在率定期和检验期拟合精度及相关性。

1 研究区域概况

三峡水库位于四川盆地与长江中下游平原交界处,控制长江上游流域面积约100万km2,占长江流域总面积的55.6%。三峡水库蓄水后形成的库区长达663余km,属河道型水库,平均宽度1.63 km,水面面积达1 000余km2,总库容393亿m3。三峡水库除了具有防洪、发电和航运作用外,也是重要水源地,三峡库区人口稠密,工农业、生活用水直接关系到国计民生。水面蒸发水量损失占水库、湖泊等自然水体水量损失的比例大,为研究三峡库区水面蒸发变化规律和估算库区水面蒸发损失量,2013年8月1日设立巴东漂浮水面蒸发实验站(以下简称“巴东站”,110°22′E,31°03′N),2017年国家批准为水文站。巴东站位于长江三峡库区湖北省恩施州巴东县信陵镇沿江路38号右岸,距三峡大坝71 km,设有陆上蒸发观测场和漂浮蒸发观测场,陆上观测场场地高程183 m(吴淞资用),观测项目有降水量、蒸发量、气温、相对湿度、大气压、水汽压、风速风向、水温(蒸发池内)、日照,多年来为研究三峡库区水面蒸发量及其变化规律收集大量基本资料。本文根据巴东站2013年8月至2022年7月实测数据对蒸发模型进行分析,研究选取2013年8月至2020年7月共84个月资料作为模型率定期,以2020年8月至2022年7月共24个月作为模型检验期,采用SCE-UA[8]自动优化算法,以确定性系数最高和蒸发总量相对误差绝对值最小为目标,通过Matlab自编程序进行模型参数的优化率定。

2 研究方法

气温、风速、相对湿度等气象因子对水面蒸发都有很大的影响,在进行模型构建之前,需要通过相关性分析正确认识水面蒸发量与气象因子之间的关系,以获取相关性强的影响因子进行水面蒸发模型研究,进一步提高模型模拟精度。巴东站陆上观测收集的气象因子见表1。考虑资料的年系列情况,经分析计算后,采用以月尺度进行模型构建;首先基于日序列统计资料得到月序列资料,再分别采用灰色关联度、偏相关系数分析研究陆上月蒸发量与各气象因子的相关度。巴东站陆上水面蒸发与气象因子相关性计算结果如表2所示。

表1 巴东站蒸发气象因子Tab.1 Meteorological factors of evaporation at Badong Hydrological Station

表2 蒸发与气象因子相关性统计Tab.2 Correlation between land surface evaporation and meteorological factors

由表2可知,灰色关联度ζ、偏相关系数r的值有一定差异,但是灰色关联度与偏相关系数所体现的相关程度较一致,相关指数大于0.8的有:月平均水气温水汽压差、月日照小时数、月平均气温及蒸发池内月平均水温,说明这几项对蒸发的影响较大。

水面蒸发是一个非常复杂的过程,影响因素多。水面蒸发量模型的研究已有200多年的历史。自19世纪80年代以来得到许多研究成果,但绝大多数蒸发模型是利用局部地区单站观测资料,由经验公式分析取得的纯经验模型或半经验模型。本文结合巴东站测站特性、地理位置、气象因子相关性、资料序列等,采用灰色关联度、偏相关系数以及适用性综合分析后,选用经验公式、修正模型以及数学模型等方法,对巴东站陆上蒸发模型进行分析。

3 模型构建及计算结果分析

3.1 通用公式及其计算结果

由濮培民等提出的通用公式,分析了水面蒸发过程中水-气界面上质量、能量和动量传递过程以及水文、气象要素对水面蒸发的线性影响[9],用鲍文比和层结稳定度两个无量纲量,结合蒸发有效风速,建立水面蒸发量的计算模型。根据本站收集到的蒸发、气象资料,不仅包括气温还有蒸发池水温、水汽压、风速等数据,满足通用公式的计算,计算公式如下:

(es-ea)

(1)

式中:μ为水面以上风速,m/s;ΔT为水汽温差,℃;es为水面水汽压,hPa;ea为水面以上1.5 m处空气中的水汽压,hPa;当ΔT≥0时,c=0,当ΔT<0时,c=0.01;此模型不包含气压、相对湿度因子。

由通用公式精度评定(表3)和通用公式模拟与实测月水面蒸发量变化过程(图1)可以看出,通用公式模型率定期的确定性系数为0.939 3,蒸发总量相对误差为0.13%,模型模拟的蒸发过程与实测过程较一致,效果较好;检验期的确定性系数较小,效果较差。总体而言,蒸发量计算值与观测值的相关性较好,总体模拟结果比较理想,后续还需加强分析。

图1 通用公式模拟与实测月水面蒸发量变化过程Fig.1 Simulation and measurement of monthly water surface evaporation by general formula

表3 通用公式精度评定Tab.3 Accuracy evaluation of general formula

3.2 李万义修正模型及其计算结果

李万义公式对水面蒸发物理过程作了部分假设,适用于全国范围的水面蒸发量计算模型,此模型结构比较简单[10]。水面蒸发是在一定的热力学条件与动力学条件的共同作用下产生的,英国学者彭曼根据水面蒸发的形成机制,通过联解空气动力学方程和能量平衡方程,得出计算水面蒸发的组合型公式,该公式是依据英国特定的海洋性气候条件下取得的实验资料建立的,而中国绝大多数地区处在典型的季风气候区,因此原型彭曼公式不宜在中国应用[11]。结合本站收集的数据,依据李万义公式的框架和彭曼公式[12],进行模型构建,拟建立李万义修正公式(LWY)如下:

(2)

式中:a,b,c,d,f为待定参数;ez为饱和水汽压,hPa,由蒸发器内水温和气温综合求得;R为平均相对湿度,以小数计;el为实测平均水汽压,hPa;T为气温,℃;此模型未包含气压因子。

模型涉及的参数有5个。本研究选取2013年8月至2020年7月共84个月资料作为模型率定期,以2020年8月至2022年7月共24个月作为模型检验期,采用SCE-UA[8]自动优化算法,以确定性系数最高和蒸发总量相对误差绝对值最小为目标,通过Matlab自编程序进行模型参数的优化率定。经过模型率定后,得出LWY水面蒸发模型参数及精度评定结果见表4和图2。

图2 LWY模拟与实测月水面蒸发量变化过程Fig.2 LWY simulation and measured monthly water surface evaporation process

表4 LWY水面蒸发模型参数及精度评定Tab.4 Parameters and accuracy evaluation of LWY water surface evaporation model

由表4和图2可以看出,无论是检验期还是率定期,LWY模型的确定性系数均超过0.90,蒸发总量相对误差均在±7%以内。模型模拟的蒸发过程与实测过程较一致,检验期的蒸发相关散点在率定期范围内,蒸发量计算值与观测值的相关性较好,总体模拟结果比较理想,表明LWY水面蒸发模型构建准确,精度较高。

3.3 回归模型分析及其计算结果

由于气象因子与水面蒸发存在较为显著的线性相关性,故从多元线性回归[13]角度考虑构建水面蒸发线性回归模型,采用偏最小二乘法(PLS)回归模型进行参数率定,得到如下回归模型:

E=a1+a2R+a3U+a4e+a5S+

a6T+a7B+a8TS+a9P

(3)

式中:a1～a9为模型待定参数。

模型涉及的参数有9个。表5给出了PLS水面蒸发模型参数及精度评定结果。图3为回归模型与实测月水面蒸发量变化过程。

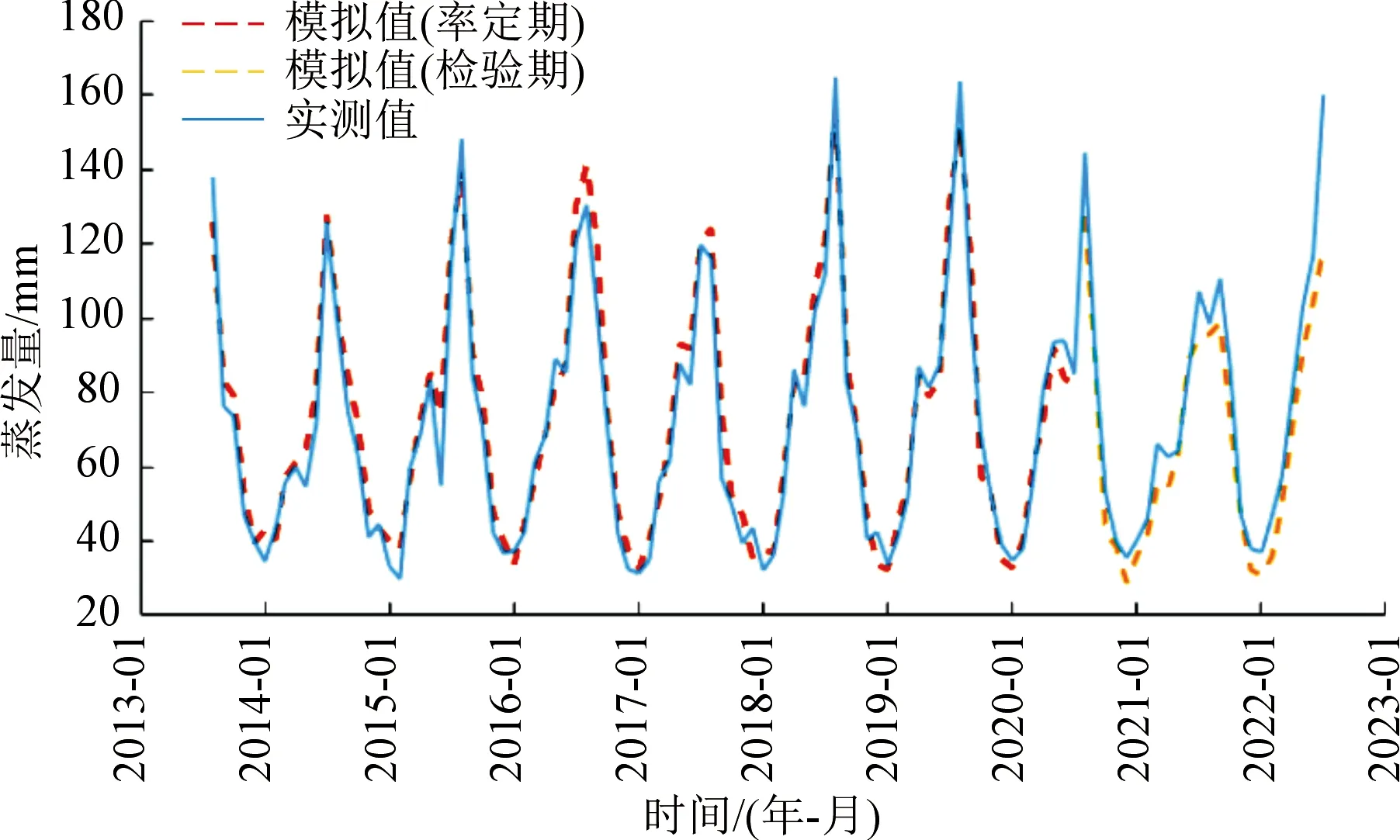
图3 回归模型与实测月水面蒸发量变化过程Fig.3 Regression model and measured monthly water surface evaporation process

表5 回归模型参数及精度评定Tab.5 Regression model parameters and accuracy evaluation

由图3和表5可以看出,采用回归模型进行月蒸发的模拟同样表现出较高的精度。无论是检验期还是率定期,模型确定性系数超过0.90,蒸发总量相对误差在率定期较小,检验期偏大,参数率定有较好的效果,能够较好地拟合水面蒸发变化过程。

3.4 复杂数学模型及其计算结果

随着计算机技术的不断提高,一些复杂数学蒸发模型[14-15]也被运用到相关指标的模拟。最为常见的有人工神经网络(BP、ELM)[16]。本文尝试采用BP和ELM人工神经网络进行水面蒸发模拟。经过模型率定后,得出人工神经网络(BP、ELM)水面蒸发模型参数及精度评定结果,见表6和图4～5。

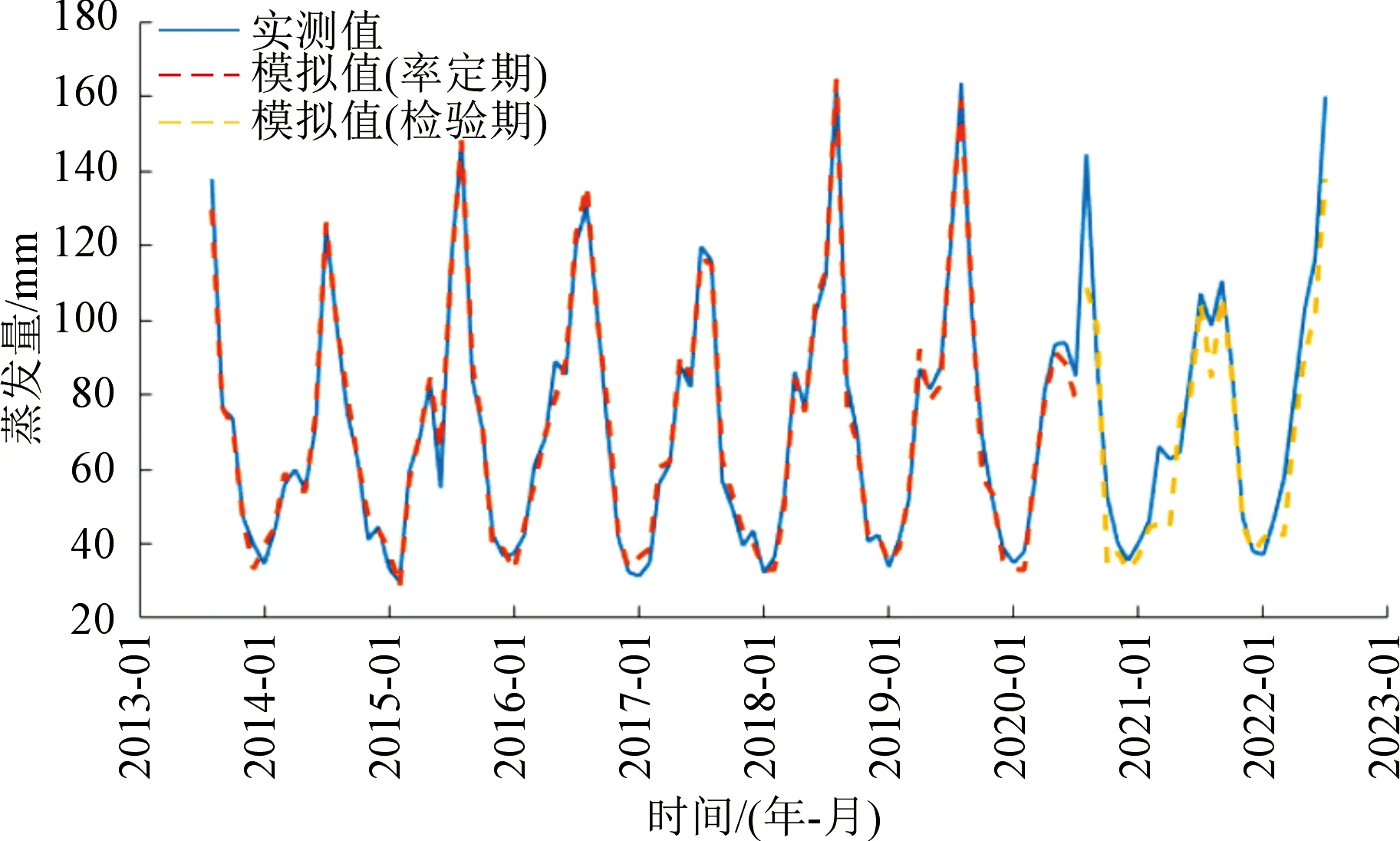
图4 ELM神经网络模型与实测月水面蒸发量变化过程Fig.4 ELM neural network model and measured monthly water surface evaporation process

图5 BP神经网络模型与实测月水面蒸发量散点图Fig.5 BP neural network model and scatter chart of measured monthly water surface evaporation

表6 神经网络模型参数及精度评定Tab.6 Neural network model parameters and accuracy evaluation

由图4～5和表6可以看出,采用人工神经网络(BP、ELM)进行月蒸发的模拟同样表现出较高的精度,率定期模型确定性系数均超过0.90,但BP模型在检验期表现相对较差;蒸发总量相对误差在率定期较小,检验期偏大。

4 水面蒸发模型分析

本次研究共采用5种方法构建水面蒸发模型,分别是回归模型(PLS)、李万义修正模型(LWY)、通用公式、BP神经网络、ELM神经网络。各模型的模拟精度存在差异,为更好地对模型的适用性进行比较分析,各种月模型在检验期、率定期的指标(确定性系数和总量相对误差)见图6～7。

图6 各模型确定性系数Fig.6 Deterministic coefficients of each model

图7 各模型蒸发总量相对误差Fig.7 Relative errors of total evaporation of each model

由图6～7可知,5种模型构建准确,各模型模拟精度均较高,率定期各模型确定性系数均高于0.90,总量误差控制在±10%之间,均适用于陆上月尺度蒸发量的模拟;在率定期,相比PLS、LWY、通用公式、BP神经网络这4种模型,ELM神经网络模拟精确相对较高,确定性系数最高0.992 3,且蒸发总量相对误差的绝对值也最小,模型适用性最强;在检验期,则是LWY相对效果较好。综合分析,LWY更优,更能适用巴东站陆上水面蒸发计算。

5 结 论

本文结合巴东站气象数据,对三峡库区巴东站陆上蒸发模型进行研究,选取2013年8月至2020年7月共84个月资料作为模型率定期,以2020年8月至2022年7月共24个月作为模型检验期。分别采用回归模型(PLS)、李万义修正模型(LWY)、通用公式、BP神经网络、ELM神经网络,共5种方法构建水面蒸发模型,5种模型构建准确,各模型模拟精度均较高,率定期各模型确定性系数均高于0.90,总量误差控制在±10%之间,均适用于陆上月尺度蒸发量的模拟。各模型的模拟精度存在差异,率定期ELM神经网络模拟精确相对较高,各统计指标更合理,但检验期LWY相对效果更好,各统计指标更合理。总体来说,LWY更适合作为巴东站陆上蒸发模型使用,PLS、通用公式、BP神经网络、ELM神经网络构建水面蒸发模型均可作为参考使用。