变化环境下基于回归分析的非一致性水文频率计算方法
许 斌,刘 宇,吴子怡,霍军军
(1.长江科学院 水资源综合利用研究所,湖北 武汉 430010; 2.流域水资源与生态环境科学湖北省重点实验室,湖北 武汉 430010; 3.广东省水利电力勘测设计研究院有限公司,广东 广州 510635;4.生态环境部珠江流域南海海域生态环境监督管理局 生态环境监测与科学研究中心,广东 广州 510610)
0 引 言
环境在一定时期内保持稳定时,影响水文序列的因素在一定时间内也会呈现出比较稳定的变化规律,此时水文序列是在比较一致的环境下形成的,即满足“一致性”要求[1]。然而,由于气候变化和人类活动的影响,环境往往处于一定的渐变或突变之中,常常造成水文序列的影响因素在一定时期内也发生缓慢的渐变或者剧烈的突变,对水文序列中的确定性成分[2]产生一定的影响,进而导致水文序列出现了“非一致性”,从统计学的角度来看,即水文序列的统计分布参数、形式在整个时间序列范围内发生了显著变化[3]。
有学者从水文模型的角度,通过模拟径流的变化,提出了针对非一致性水文序列的频率计算途径[4-6],但由于适用性、复杂性的影响,应用区域比较有限。在统计方法上,目前常用的水文序列“还原”或“还现”修正计算,即考虑河道外用水、蒸发等水量对水文序列进行“一致性”修正[7-10],可以对流域内人类活动造成的水量变化起到一定的作用,但是却不能反映气候变化和流域下垫面变化间接引起的径流量变化问题,也无法适应过去、现状和未来不同时期环境的变化趋势[11]。谢平等提出的非一致性水文频率计算原理[12],通过对水文序列确定性和随机性成分的分解和合成计算,发展出了基于跳跃分析[13]、趋势分析[14]、降雨径流关系[15]、希尔伯特-黄变换[16]、小波分析[17]等非一致性水文频率计算方法,并进行了水资源评价等方面的应用。上述非一致性水文频率计算方法,在线性和非线性确定性成分拟合函数形式和阶数选取方面仍存在较大的主观性,且无法反映水文序列影响要素的作用。
针对非一致性水文频率计算方法中仍然存在的问题,本文提出了一种基于回归分析的非一致性水文频率计算方法。该方法与以往的非一致性水文频率计算方法不同,并非仅仅考虑了时间序列自身在时间尺度上统计规律的变化,而是结合了物理成因的因素,在构建了分析序列与影响因素之间关联性的基础上,介于统计方法和水文模型之间的一种方法,具有资料收集便捷、能够反映物理成因变化的特色,同时减少了人为主观性影响的特点。
1 基于回归研究分析的非一致性水文频率计算方法
基于回归分析的非一致性水文频率计算方法仍然是在非一致性水文频率计算原理的基础上进行构建,如图1所示。非一致性水文频率计算方法之间最大的不同之处在于水文序列组成的分析环节,基于回归分析的水文序列组成分析具体计算过程如图2所示。

图2 基于回归分析的随机性与确定性成分提取流程Fig.2 Flowchart of random and deterministic component extraction based on the Regression Analysis
首先,利用水文变异诊断系统[18],分析研究水文要素(因变量Y)及其影响因素(自变量Xi)的时间序列变异情况,并对所有的变异点进行识别。其次,在变异点中选取时间最早的变异点作为时间节点,在此之前的所有序列均为满足一致性要求的随机序列。第三,利用回归分析方法(一元到多元回归均可)构架最早变异点之前因变量Y和自变量Xi的回归模型,并对模型的有效性进行检验。然后,由于自变量Xi相对独立,根据自变量Xi水文变异情况,分别推求其随机性成分,形成自变量Xi完整的随机序列,并将其带入回归模型,推求最早变异点之后,因变量Y的随机性成分。最后,根据非一致性水文频率的分解合成原理,在最早变异点之后,因变量Y的随机性成分和实测值之间差值取均值,即为因变量Y的确定性成分。
在提取出随机性成分和确定性成分之后,根据非一致性水文频率计算原理,对随机性成分,利用P-Ⅲ型曲线进行频率计算,从而获得随机性成分在频率域上的随机规律,并结合确定性成分的预测值进行合成计算,推求合成序列的频率分布,即可得出过去(纯随机)、现状(含确定性成分)水文序列的频率分布,为变化环境下的水文频率分析提供依据。
2 研究实例
2.1 研究区域数据概况
鄱阳湖是中国最大的淡水湖泊[19],它上游承接赣江、抚河、信江、饶河及修水等河流入流,同时保持着与长江的自然联通,湖泊水位影响因素较多。近年来,受环境变化的影响,鄱阳湖蓄水量减少、水位异常偏低的事件日益增多[20],说明鄱阳湖水位出现了较为明显的非一致性,已经造成周边取水困难、湿地萎缩等生态环境问题。鄱阳湖水文气象站点位置示意见图3。

图3 水文气象站点位置示意Fig.3 Schematic diagram of hydrological and meteorological stations location
在对鄱阳湖水位的已有研究中,对于水位序列非一致性的考虑仍较为欠缺,相关的研究成果较少。本文以鄱阳湖水位为研究对象,对准确把握鄱阳湖在变化环境下的水文变异特征、非一致性水位演变规律,具有一定的现实意义。根据水量平衡原理,鄱阳湖水位的主要影响因素包括河道入流、蒸发、降水、湖泊出流、长江干流水量等。其中河道入流采用鄱阳湖五河七口控制站外洲、梅港、李家渡、虎山、石镇街、渡峰坑、万家埠、虬津年的平均流量数据,序列为1960~2013年。降水序列为中国气象数据网提供的鄱阳湖流域赣州、遂川、井冈山等14个雨量站,采用泰森多边形法得出的流域年均降水数据,序列为1960~2018年。结合国际粮农组织(FAO)推荐的Penman-Monteith方法,计算得出流域年均潜在蒸发数据。湖泊出流、鄱阳湖水位采用湖口站1950~2016年的实测数据。长江干流水量则采用九江水文站1960~2018年(根据汉口站插补延长)的流量数据。鉴于水文变异分析,需要所有时间序列起止年份保持一致,因此,最终采用的时间序列为1960~2013年。
2.2 水文变异特征识别
水文变异诊断系统常被用来识别非一致性水文序列,耦合多种检验方法的诊断系统,具有水文变异诊断检验结果唯一、可靠等优点。
在第一信度水平α=0.05,第二信度水平β=0.01的条件下,利用水文变异诊断系统对鄱阳湖水位及其影响因素年均序列进行变异诊断,其诊断结果如表1所示。

表1 鄱阳湖水位序列及其影响因素变异诊断结果Tab.1 Diagnosis result of water level series and the influence factors of Poyang Lake
从表1中可以看出,除了鄱阳湖湖口水位于2003年发生了跳跃向下的变异之外,其余水文序列的分布参数并未发生明显变化,均处于无变异的状态,这种情况可能跟选取的时间序列为年均值有关系。
2.3 非一致性频率分析
2.3.1多元回归分析模型构建
根据鄱阳湖水位及其影响因素年均序列的变异诊断结果,最早变异点即唯一变异点为2003年,变异点之前的时间序列满足一致性的要求。以鄱阳湖水位为因变量Y,水位影响因素为自变量Xi,利用1960~1993年(共34 a)水文序列构建五元一次回归分析模型,如式(1)所示。
YSW=7.88+7.05×10-4Xhk+2.46×10-4Xjj-
1.94×10-3Xjs-1.93×10-2Xzf-
5.76×10-4Xrl
(1)
式中:YSW为湖口水位;Xhk为湖口流量;Xjs为湖区降水;Xzf为湖区蒸发;Xrl为五河入流;Xjj九江流量。
为了验证回归分析模型的拟合效果,利用1994~2003年(共10 a)水文序列进行验证,以相对误差[-10%,10%]作为模型评判标准,式(1)拟合的合格率为100%,拟合效果较好,可以用于鄱阳湖水位变异点之后随机性成分的提取,如表2所示。
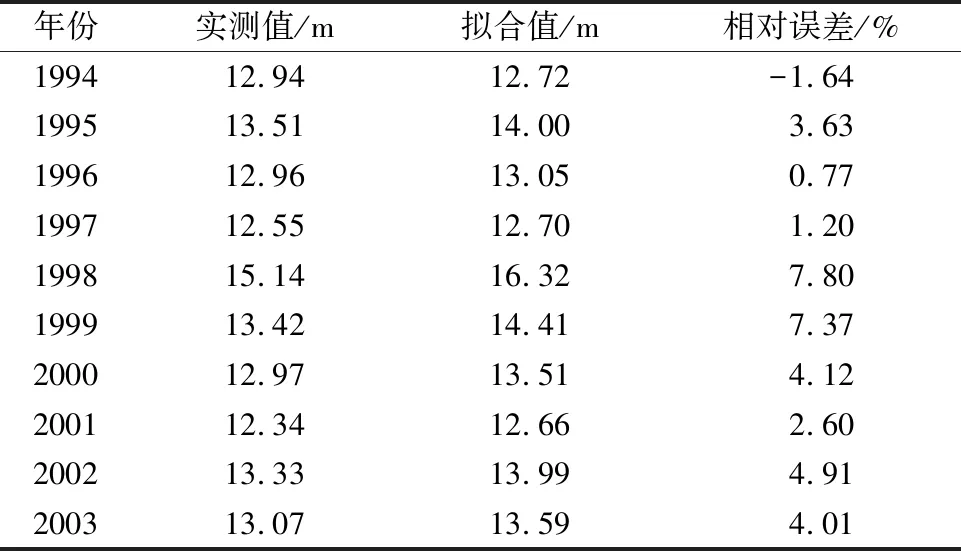
表2 回归分析模型拟合效果验证Tab.2 Fitting effect validation of Regression Analysis model
2.3.2随机性和确定性成分提取
依据式(1)以及变异点之后的鄱阳湖水位影响因素年均序列,计算2004~2013年鄱阳湖水位的随机性成分,并根据其与实测水位序列的差值,计算变异点之后鄱阳湖水位序列的确定性成分为-0.13 m,如表3所示。

表3 鄱阳湖水位确定性成分计算结果Tab.3 Deterministic component calculation results of water level of Poyang Lake
2.3.3随机性成分频率计算
由回归模型模拟得到的鄱阳湖年均水位序列随机性成分是具有一致性的稳定序列,对于满足一致性的随机性成分可以直接采用传统的频率计算方法推求其频率分布。对于年均水位序列的随机性成分,假设其服从P-Ⅲ型分布,采用有约束加权适线法计算频率曲线参数,得到均值X=12.78 m、变差系数Cv=0.07,偏态系数Cs=0.35,样本点据与频率曲线拟合的效率系数R2=97.10%。频率计算结果见表4,曲线变化如图4所示。
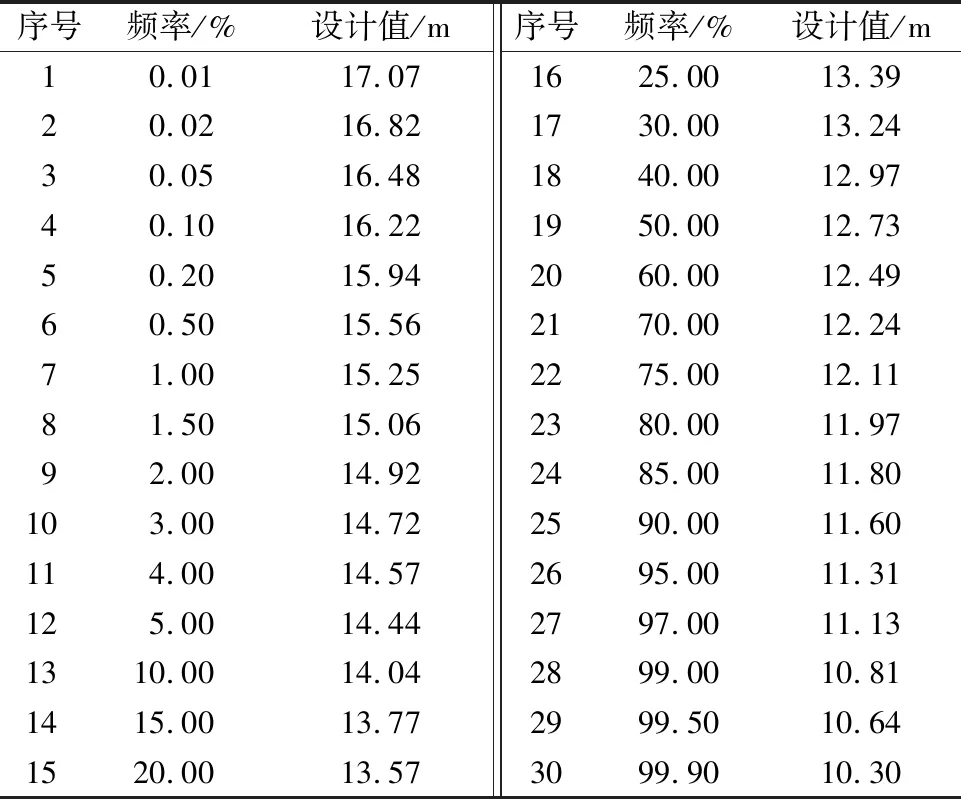
表4 年平均水位序列随机性成分频率计算结果Tab.4 Frequency calculation results of random component of water level series

图4 年平均水位随机性成分频率曲线Fig.4 Frequency curves of random component of water level series
2.3.4非一致性水位序列合成计算
采用分布合成方法进行非一致性年径流序列的合成计算。首先根据随机性成分的统计特征进行统计试验,结合鄱阳湖水位年均序列的确定性趋势成分,随机生成年均年径流合成样本点据(N=5 000),并统计不小于每一个样本点据的次数n,然后用期望值公式计算每个样本点据的经验频率。采用有约束加权适线法对合成样本序列进行P-Ⅲ型分布频率曲线计算,得出现状条件下合成序列的均值X=12.66 m,变差系数Cv=0.08,偏态系数Cs=0.35,理论频率曲线与样本点据的拟合效率系数R2=97.10%。其频率曲线如图5所示,频率计算结果见表5。

表5 年平均水位合成序列频率计算结果Tab.5 Frequency calculation results of synthesis component of water level series
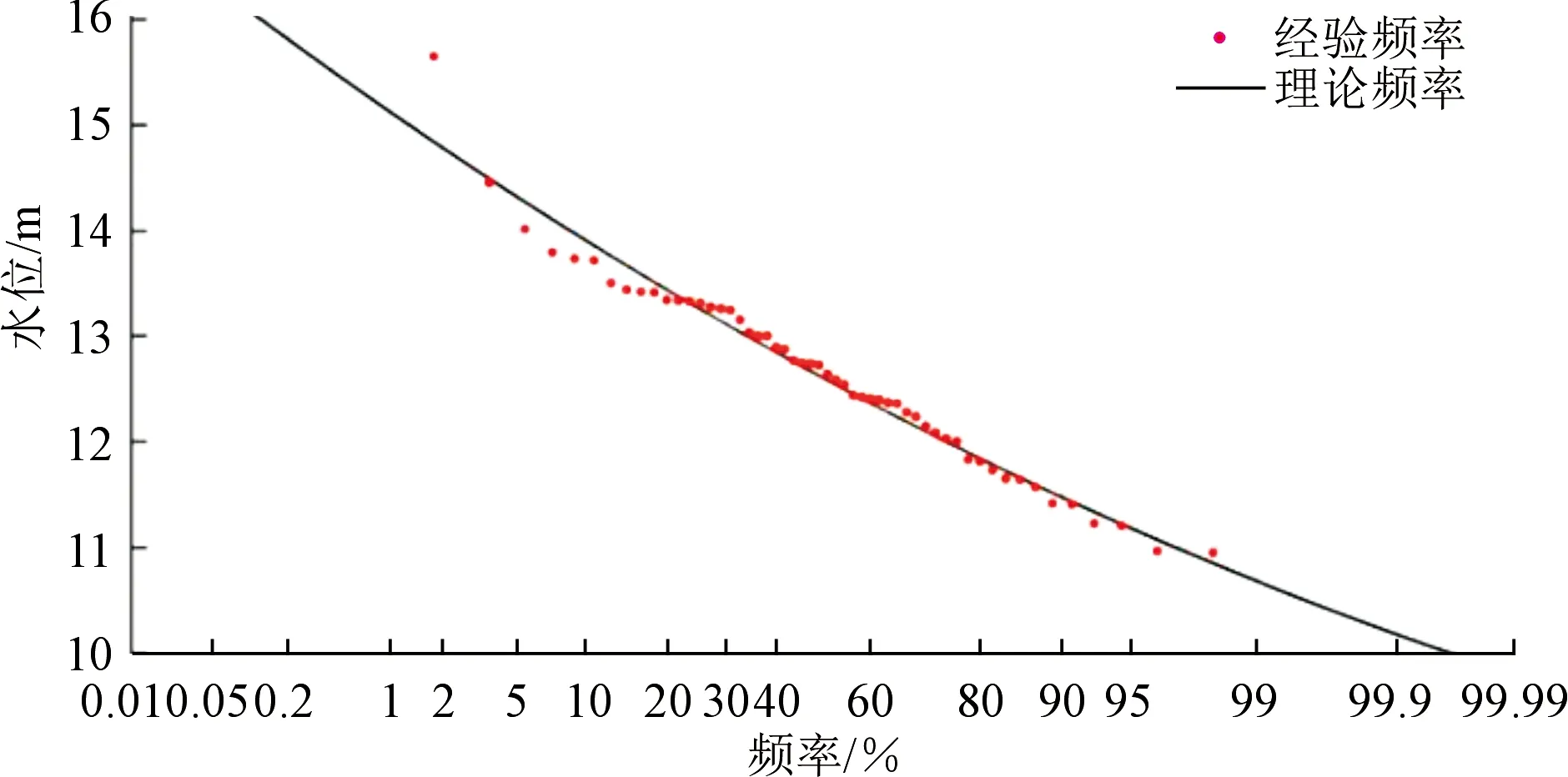
图5 年平均水位合成序列频率曲线Fig.5 Frequency curves of synthesis component of water level series
2.3.5不同时期的水位频率变化规律
随机性成分的频率计算结果可以反映过去近似天然条件下水位的形成条件,确定性成分与随机性成分的合成序列,可以反映现状(水文变异后)径流的形成条件。
对于鄱阳湖年均水位而言,其变化的总体趋势是减少的,过去、现状两个时期的鄱阳湖年平均水位均值的评价结果为12.78 m、12.65 m。现状与过去相比水位均值相比减少0.13 m,占过去水位均值的1.02%。现状与过去相比较,在丰水年(频率为0.01%~30%)、平水年(频率为30%~60%)、枯水年(频率为60%~ 99.9%),其水位较少的幅度分别为0.76%~0.98%,0.98%~1.04%及1.04%~ 1.26%。
3 结 论
针对非一致性水文频率计算方法中仍存在的参数选取主观性强、无法反映多影响要素的问题,本文提出了基于回归分析的非一致性水文频率计算方法。该方法借助回归分析的途径,考虑了物理成因的因素,减少了人为主观性影响,是一种介于统计方法和水文模型之间的一种方法。同时对鄱阳湖水位及其影响因素水文序列进行实例研究,表明该方法具有可行性。
本方法计算的结果显示,鄱阳湖年均水位序列呈现出下降的趋势,枯水期出现的频率有所提升,重现期缩短,分析结果与鄱阳湖实际的水位状况较一致,说明本方法具有可靠性。本方法所需资料收集便捷、能够反映物理成因变化,在变化环境下非一致性水文频率计算方面,将具有很好的应用前景。

