基于熵权的全局记忆LF蚁群聚类算法

熊伟超　蒋瑜

摘 要：针对LF蚁群聚类算法没有区分数据集属性重要度、算法效率低和聚类效果不稳定的问题，提出一种基于熵权的全局记忆LF算法（weighted global ant colony optimization，WGACO）。该算法首先通过熵权法计算各属性熵权，修改欧氏距离计算公式，以提升聚类精度；使用权重最大的属性值对数据对象进行初始化，增强聚类效果的稳定性；引入全局记忆矩阵减少蚂蚁的无效移动，提升算法效率；加入算法的收敛条件，提升算法实用性。选取UCI数据库中的7个真实数据集和3个人工生成的数据集进行数值实验，并与GMACO、SMACC、ILFACC三种改进LF的算法进行比较，实验结果表明，所提算法在精度、算法效率和稳定性上都有比较好的提升，在处理高维数据上也有较好的表现。最后，WGACO在商场会员用户细分上表现良好，体现了其实用价值。

关键词：LF蚁群聚类；信息熵；属性权重；全局记忆

中图分类号：TP18 文献标志码：A 文章编号：1001-3695（2023）10-026-3053-06

doi：10.19734/j.issn.1001-3695.2023.02.0046

Global memory LF ant colony clustering algorithm based on entropy weight

Xiong Weichao，Jiang Yu

（College of Software Engineering，Chengdu University of Information Technology，Chengdu 610200，China）

Abstract：Aiming at the problem that LF ant colony clustering algorithm does not distinguish the importance of data set attri-butes，the algorithm efficiency is low and the clustering effect is unstable，this paper proposed a weighted global memory ant colony optimization （WGACO） based on entropy weight.Firstly，it calculated the entropy weight of each attribute by entropy weight method，and modified the Euclidean distance calculation formula to improve the clustering accuracy.It initialized the data object with the value of the largest weight attribute to enhance the stability of the clustering effect，and introduced the glo-bal memory matrix to reduce the invalid movement of ants and improve the efficiency of the algorithm.It added the convergence conditions of the algorithm to improve the practicability of the algorithm.Selecting seven real data sets and three artificially generated data sets in UCI database for numerical experiments，and compared WGACO with GMACO，SMACC and ILFACC three improved LF algorithms.The experimental results show that WGACO has a relatively good improvement in accuracy，algorithm efficiency and stability，and also has a good performance in processing high-dimensional data.Finally，WGACO has performed well in the segmentation of mall member users，reflecting its practical value.

Key words：LF ant colony clustering;information entropy;attribute weight;global memory

0 引言

聚類技术能够根据数据本身发现其内在规律，经常作为数据挖掘中重要的预处理步骤。为了应对各种各样的数据，越来越多的聚类算法被提出。蚁群聚类算法通过模拟自然界中工蚁堆积蚂蚁尸体的行为实现聚类，相比于传统聚类LF算法无须指定聚类个数、算法鲁棒性更强、更易实现并发分布式计算，并具有抗噪声数据的特点。但是，蚁群聚类算法也存在算法效率较低和算法参数较多的缺点。Deneubourg等人［1］通过研究自然界蚂蚁堆积尸体的行为，提出了解释蚁群聚类现象的BM（basic model）模型。Lumer等人［2］在BM模型的基础上提出了LF算法。随后，众多学者的改进主要围绕着提升算法效率和降低算法参数影响。

在提升算法效率上，刘艳等人［3］加入了信息素来控制蚂蚁移动的随机性，并通过减少数据集属性维度有效地提高了算法聚类效率。牛永洁［4］利用全局记忆矩阵代替之前蚂蚁的局部记忆，蚂蚁在全局信息下向最优位置移动而不是直接跳转到该位置，减少了蚂蚁的无效移动并避免陷入局部最优。高阳［5］通过Spark平台实现了算法的并行处理，增加了算法对大量数据的处理能力。王昕宇等人［6］在文献［4］的基础上加入了首次找准原则和相异原则，加快了蚂蚁找到数据的速度，提升了算法效率。沈兴鑫等人［7］设计了相似度矩阵，将蚂蚁随机移动方式优化为按照相似度系数规则实施目的性的关联，加速了数据聚集。Chen等人［8］赋予蚂蚁更快的搬运速度，减少算法迭代时间。

在降低参数影响上，朱峰等人［9］通过蚂蚁放下数据对象失败的次数与迭代次数的比值设计了聚类精细程度参数alpha的数值变化公式，实现了alpha参数的自适应。刘阳阳等人［10］根据先粗分再细分的思想，阶段性地递减蚂蚁可视范围R，实现了R参数的自适应，并且设计了算法结束条件，使算法能够自主完成收敛，提高了算法的实用性。甘泉等人［11］利用区域数据的信息熵变化代替了蚂蚁“拾起”“放下”的判断条件，减少了算法参数个数。同时，不少学者对蚁群聚类算法的其他方面也进行了改进。徐晓华等人［12］在BM模型基础上提出AM（ant movement）模型，把数据对象本身当做蚂蚁，用睡眠态、激活态代替数据的捡起和放下，有效避免蚂蚁的无效移动，提高了聚类的速度和质量。Wei［13］加入数据组合机制，采用抽象的蚁群聚类算法对基准问题进行了聚类，能够有效地用于多变量聚类。此外，蚁群聚类算法还被应用在了复合物挖掘［14，15］、用户细分［16］等领域。通过对上述的算法改进和算法本身分析发现，LF的算法效率还可以进一步提升，独立重复运行时，算法效率和性能波动较大的问题没有被解决。

因此，本文提出一种基于熵权的全局LF蚁群聚类算法WGACO。该算法首先使用熵权法，通过信息熵计算数据集各属性权重，并修改欧氏距离的计算公式，使用权重最大的两个属性值对数据对象进行坐标初始化；同时，引入一个全局记忆矩阵和算法收敛条件。与其他改进的算法相比，本文算法聚类精度更高、聚类速度更快、算法稳定性更强。

1 LF蚁群聚类算法

LF算法将待处理的数据对象和蚂蚁都随机投影到一个指定大小的二维网格中，并限制一个网格中只能有一个数据对象。蚂蚁在网格中碰到一个数据对象Oi后，用式（1）计算Oi在当前区域中的局部密度f（Oi）。

其中：d2表示数据Oi领域的大小；d（i，j）表示Oi与其领域中其他数据对象之间的欧氏距离；α为聚类的精细度，α过大，不同类数据对象之间的区分不明显，聚类的效果变差，α过小，同类数据对象间差异被放大，聚类后簇的个数会多于实际的簇数，算法运行时间也会变长。

用式（2）将f（Oi）转换为蚂蚁捡起Oi的概率。

其中：Kp是蚂蚁捡起Oi的难度系数。如果Ppick大于一个随机数，蚂蚁捡起Oi，在自己的记忆中找到与Oi最匹配的位置后，蚂蚁携带Oi向该位置随机移动。携带Oi的蚂蚁移动到新位置后，如果该位置没有被占用，首先用式（1）计算f（Oi），之后用式（3）将f（Oi）转换为蚂蚁在该位置放下Oi的概率Pdrop。

其中：Kd是蚂蚁放下Oi的难度系数。如果Pdrop大于一个随机数，蚂蚁在该位置放下Oi，并在自己的记忆中记录该位置，之后重复之前的动作，蚁群经过若干次迭代后就能够实现对所有数据对象的聚类。

2 基于熵权的全局LF蚁群聚类算法

2.1 熵权法

在数据集中每个属性对聚类的贡献程度不同，区分不同属性的重要度能提高聚类的准确度、加速聚类。在统计学中，某个数据属性信息熵越小，數值离散程度越大，则认为该数据属性包含的信息越多，对应的权重越大。熵权法是一种通过各数据属性本身的信息熵计算对应权重的方法，并会对得到的结果进行一定的修正，使得到的属性权重较为客观。对第j个数据属性，用式（4）计算其信息熵。

2.2 稳定的数据初始化策略

在LF算法中，数据对象的初始位置是随机的。由于数据集中的数据对象S可以与多个类的数据对象聚集，算法独立重复运行时，每次随机得到的初始化结果不同，S周围数据对象的分布情况都不一样，导致S有时候先碰到同类对象被正确聚集，有时候先碰到异类对象被错误聚集，S对象数量越多，算法聚类效果波动越大，下文给出了数据对象S的定义。每次随机初始化后，同类对象之间的距离也不同，距离短算法迭代快，距离长算法迭代慢，算法运行时间也有较大波动。图1是LF在UCI数据集iris、wine、seed上独立重复运行10次的运行时间和ARI［17］数值，从图中可以观察到，LF算法的聚类效率和聚类精度波动较大，验证了上述分析，随机初始化的方式的确会影响LF的稳定性。

为了增强算法效率的稳定性，需要一个稳定的初始化结果，同一个对象初始化位置固定，为了解决算法精度不稳定的问题，使S能够被正确聚集，需要使S周围有更多的同类对象，增加其在被搬运过程中先碰到同类对象的概率。考虑数据对象本身的属性值是不变的，并且同类对象在同一属性上的值相近。因此，使用数据对象自身属性值对其进行坐标初始化可以得到稳定的初始化结果，并且同类对象在网格上的位置接近，S周围也会有更多的同类对象。由于同类对象在权重最大的属性上值最接近，异类对象在该属性上值最不同。所以，在数据集所有的属性中，使用权重最大属性值对数据对象进行初始化可以使同类对象在网格上的位置最接近，并且不同类别的对象所处的区域有明显的间隔，更容易执行聚类操作。具体定义如下：

定义1 数据对象S。与同类对象和异类对象在欧氏距离度量上区分不明显，容易被错误划分的对象。

定义2 权重最大属性。数据集中，在数据对象分类中贡献度最大的属性。

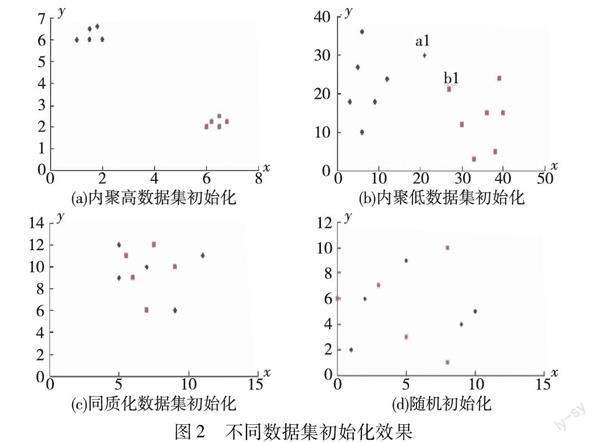
聚类数据集根据自身特点可以划分为数据内聚度较高数据集、数据内聚度较低数据集和高维数据集。图2是不同类型数据集的初始化效果，图（a）～（c）是使用权重最大属性值初始化的理想效果，图（d）是随机初始化效果。接下来结合图2分析使用权重最大属性值初始化在不同类型数据集上的普适性：

a）数据内聚度较高的数据集。该类数据集是比较理想的聚类数据集，图（a）是这类数据集使用权重最大属性值初始化的效果。因为数据内聚度高，所以，这类数据集一般没有S对象，初始化后不会提升聚类精度及其稳定性。但是从图中可以看出，同类对象初始位置非常接近，甚至能够达到初步聚类的效果，算法效率会得到显著的提升。

b）数据内聚度较低的数据集。大多数真实数据集属于该类。图（b）是这类数据集使用权重最大属性值初始化的结果，由于数据内聚度低，类之间的边界不明显，有可能出现S对象。在LF算法中，为了避免局部最优，蚂蚁搬运对象的方向有随机因素的影响。如果图中的a1、b1为数据对象S，从a1、b1周围对象的分布情况来看，其在被搬运的过程中先碰到同类对象的概率与先碰到异类对象的概率几乎相同。如果图中的其他对象为数据对象S，其先碰到同类对象的概率远大于先碰到异类对象的概率。因此，使用权重最大属性值对该类数据集初始化不仅能够提升算法效率，还能够提升算法聚类精度。

c）维度高，不同类别对象在权重最大属性上差异较大的数据集。其初始化效果类似图（b）。高维属性往往会使各对象在欧氏距离上难以区分，所有对象之间都能够相互聚集，算法的初始化策略不会对算法效率及其稳定性产生影响。在这类数据集中，S对象的个数较多，使用权重最大属性值初始化对聚类精度的提升比较明显。

d）维度高，不同类别对象在权重最大属性上差异较小的数据集。图（c）是这类数据集初始化的效果，所有对象混杂在一起，不能实现聚类操作，初始化策略的改变无法影响其聚类效率和精度。

式（8）为按照属性值的具体初始化公式。

其中：X为数据对象在网格上的坐标；N为网格长度；i为数据对象权重最大的属性值；max为当前数据集中该属性的最大值；min为当前数据集中该属性的最小值。

2.3 全局记忆矩阵

LF算法中各蚂蚁独立执行聚类动作，蚂蚁之间没有信息交流。当一只蚂蚁将数据对象搬运到目的数据对象附近时，该数据对象可能已经被其他蚂蚁搬走，导致蚂蚁无效移动。为了实现蚂蚁之间的信息共享，引入一个三列的全局记忆矩阵，分别记录数据对象索引、数据对象在当前位置的Pdrop以及数据对象失效标志，数据对象坐标信息通过索引从对象位置矩阵中获取。加入全局记忆矩阵后，蚂蚁拾起、移动、放下的处理步骤发生变化，具体如下：

a）蚂蚁成功拾起数据对象后，如果全局记忆中存在该对象，将该对象设为失效点。

b）蚂蚁在全局记忆中找到与当前数据对象最相似的数据对象后，向目标对象随机移动。

c）蚂蚁成功放下数据对象后，在全局记忆中用当前数据对象信息替换失效对象信息，如果没有失效对象，将当前数据对象的Pdrop与全局记忆中最小的Pdrop进行比较，如果当前数据对象的Pdrop大于该Pdrop，用当前数据对象信息替换对应数据对象信息，否则全局记忆保持不变。

全局记忆矩阵的加入能够实现蚁群中的信息共享，每只蚂蚁都能作出当前最合适的选择。移动的随机性是LF算法不易陷入局部最优的关键，而移动的有向性能够加速聚类，全局记忆中蚂蚁向目标对象随机移动兼顾了移动的随机性和有向性，避免陷入局部最优的同时提升算法效率。矩阵中的失效标志列能够快速找到替换项，减少更新矩阵时的时间。

2.4 算法自主收敛

LF中算法迭代次数是固定的，次数过低聚类效果不理想，次数过高会影响算法效率。从式（1）（2）可以发现，越是到聚类后期，数据对象周围同類数据的数量越多，该对象与其领域对象之间的欧氏距离d（i，j）变得越小，区域密度f（Oi）变得越大，该对象被拾起的概率Ppick变得越小，该对象很难被蚂蚁拾起，对应蚂蚁仍保持为空载状态。类似的对象越多，网格上处于空载状态的蚂蚁就越多。因此通过算法每次迭代结束后空载蚂蚁的数量可以判断算法的聚类进度，当算法中空载蚂蚁的数量连续多次超出预设范围后，可以认为聚类基本完成。具体的收敛条件为：当算法在连续20次迭代中空载蚂蚁的数量超过总数量的90%时，算法结束。真实的数据集中难免会存在异常对象，这类对象不能与其他对象发生聚集行为，导致拾起这些对象的蚂蚁一直处于负载状态，影响算法收敛。为了避免这些数据的影响，为每只蚂蚁增加一个计数器，记录蚂蚁连续放下数据对象失败的次数，当计数器数值达到指定的次数后将当前负载的数据对象强行放下，转而去处理其他数据对象。组合以上的改进，WGACO伪代码如下。

算法1 WGACO算法

输入：数据集D。

输出：聚类结果C。

a）初始化参数如网格大小GridNum，蚂蚁数量AntNum，数据数量N，聚类精细度α，邻域半径R，拾起难度K1，放下难度K2，全局记忆容量MemorySize。

b）计算数据集各属性权重。

c）将得到的权重按照式（7）加入到欧氏距离的计算当中。

d）通过式（8）完成数据对象在网格上的初始化。

e）随机选择蚂蚁，若蚂蚁为空载执行步骤f），为负载执行步骤g）。

f）蚂蚁随机跳转到一个数据对象上，通过式（1）（2）判断能否捡起该对象。

g）蚂蚁通过式（1）（3）判断能否在当前位置放下负载的数据对象，若不能，则根据全局记忆矩阵继续移动。

h）判断算法是否收敛，收敛执行步骤i），否则继续执行步骤e）。

i）输出聚类结果。

3 算法复杂度分析

LF作为迭代的算法，其时间复杂度为O（MNK），M为迭代次数，N为蚂蚁个数，K为每次迭代中每只蚂蚁的计算量。由于N为事先指定的常数，所以LF算法的时间复杂度属于O（n2）。使用新的欧氏距离，改变数据初始化策略只是使用了不同的计算公式，在时间复杂度上没有变化。因此，WGACO的整体时间复杂度为O（MNK+T），依旧属于O（n2），T为计算属性权重的时间开销。使用权重最大属性值对数据对象进行初始化后，蚂蚁搬运数据对象的距离变短，使用全局记忆矩阵后，减少了无效迭代的次数，WGACO中的M值会明显小于LF中的M值。因此，虽然WGACO的时间复杂度与LF相同，运行效率却会明显提升。LF的空间复杂度为O（1），每只蚂蚁都拥有常数个记忆空间。WGACO引入了全局记忆矩阵，并为每只蚂蚁增加了一个计数器，依然只使用了常数个存储空间，空间复杂度依然为O（1）。

4 仿真实验及分析

4.1 实验环境与实验数据集

对比实验在Anaconda4 jupyterlab中完成。实验所用操作系统为Windows 10，处理器为Intel Core i5-8250U@1.60 GHz四核，内存为8 GB。表1为7个UCI数据集的说明，表2为三个由sklearn内置的make_blobs函数生成的数据集，其中cluster_std参数表示生成的数据集中同一类数据的方差大小。设置与GMACO［6］、SMACC［7］和ILFACC［8］三种改进LF的算法对比。

4.2 实验参数

参数设置为：Kpick=0.1，Kdrop=0.15，邻域r=2，二维网格的大小是100×100，蚂蚁个数为30，全局记忆的长度为50［4］，蚂蚁计数器的阈值为20。

从式（1）发现，适合每个数据集的α值不相同。因此，在实验前需要先多次运行算法找到适合不同数据集的α值。合适的α值应该满足以下要求：在该α值下算法能够完成收敛；同时，为了充分验证改进后算法的有效性，每个数据集取三个不同的α值进行对比实验，三个α值依次增大。表3是各个数据集在实验中的α值，第一列为在多次调试中找到的能使该数据集完成收敛的最小α值。从式（7）发现，修改后的欧氏距离计算公式缩小了属性之间的差值，导致α的取值范围发生变化。为了维持对比实验的公平，其余三种对比算法也使用式（7）计算欧氏距离，将各属性权重全部设为1/n，n为数据的属性个数。

聚类结果的评价指标使用调整兰德系数ARI（adjustable Rand index）［17］和F指标（F1-measure）［18］，ARI为［-1，1］，F1为［0，1］，值越大代表聚类效果越好。同时，记录四种算法的运行时间来评估算法效率，运行时间包含数据预处理、属性权重计算、数据集初始化、算法迭代。实验结果中的数值都为每个算法独立重复运行20次后的均值。

4.3 实验结果与分析

图3为所有数据集使用权重最大属性值初始化的效果。初始化效果符合圖2中的预期，可以看出，data1、iris、seed属于内聚度较高的数据集，data2、wine、Wdbc、wave属于内聚度较低数据集，move、cover属于在个别属性值上有明显区别的高维数据集，data3属于不能聚类的数据集。图3的实验结果证实了使用权重最大属性值初始化策略的普适性。

表4为四种算法的对比实验结果。在算法效率上，WGACO在低维数据集iris、wine、seed、Wdbc、wave上表现最好，比GMACO平均快3.43倍，比SMACC平均快2.21倍，比ILFACC快1.76倍，一方面是因为WGACO在初始化后，数据集中同类对象就能基本处于网格上的同一区域，极大地缩短了算法迭代时间。初始化效果越好，WGACO的聚类效率提升效果越明显，WGACO在初始化效果好的iris、seed、Wdbc上比其余三种算法平均快3.4倍，而在初始化效果一般的wine和wave上平均只快了1倍。因此，在数据量较小的wine数据集中，SMACC和ILFACC算法的聚类效率与WGACO相近，甚至有时能够更快。另一方面是因为WGACO中引入了全局记忆矩阵，全局记忆相比于ILFACC中的局部记忆更具时效性，属性熵权的加入使全局记忆信息更准确，避免了算法因过时、错误信息而出现的无效迭代，能够有效地提升聚类效率。在高维数据集move、cover中，WGACO相比于其余三种算法没有明显优势，这是因为较高的维度使不同簇之间的对象在距离度量上出现同质现象，所有对象互相都能产生聚集行为，数据集被聚集的速度受算法的影响变小，表4中可以发现，在最高维度的cover数据集上四种算法的聚类效率几乎没有差别。表4中黑体数据为同组中的最优值。

在聚类精度上，WGACO和ILFACC在五个低维数据集上的聚类精度整体高于GMACO和SMACC，因为这两种算法都在计算欧氏距离中加入了属性权重的调节。其中，在iris、seed、Wdbc数据集上WGACO和ILFACC的F值和ARI几乎持平，在wine和wave数据集上，WGACO的F值和ARI高于ILFACC，平均高出9%，这是因为这两种数据集数据内聚程度较低，数据对象S的个数较多。而在高维数据集move和cover中，WGACO的聚类精度明显高于其他三种算法，F值和ARI平均比GMACO高18%和25%，比SMACC高17%和24%，比ILFACC高15%和23%，因为随着数据维度的增加，在距离度量计算中无效属性对有效属性的干扰越来越大，单纯地加入属性权重的影响变小，ILFACC在两个高维数据集上的聚类精度相比于GMACO和SMACC并没有明显提升，对象是否被正确聚类更多地取决于其周围对象的分布情况。WGACO单独使用权重最大的两个属性对数据集进行初始化，能够避免其他属性的干扰，相比于ILFACC算法，能够更有效地发挥属性权重的作用。同时，全局记忆矩阵能够使蚂蚁向当前全局最优位置随机移动，避免了陷入了局部最优，而SMACC通过寻找聚类对象领域中的相似对象来决定该对象被搬运的方向，缺乏全局信息的指导，虽然其聚类速度快，但容易陷入局部最优，聚类精度不高。

在表4中观察到，随着α值的增大，四种算法都出现了聚类精度下降、运行时间减小的趋势，从α的最小值到最大值，GMACO的F值和ARI分别下降14%和22%，SMACC分别下降11%和12%，ILFACC分别下降15%和12%，WGACO分别下降4%和6%。α为聚类的精细度系数，α变大代表所有对象在蚂蚁眼中开始变得相似，此时，低维数据集中不同类别的对象开始出现不可区分的现象，其被正确聚类的概率也开始受到周围对象分布情况的影响，与上述高维数据集的情况类似。因此，使用权重最大属性初始化策略后，WGACO对α有一定的容错能力，聚类精度的下降程度要比其余三种算法小。

上述分析可以得出结论，WGACO在数据内聚程度较高的低维数据集上主要为提升聚类速度，在数据内聚程度较低的低维数据集和高维数据集上主要为提升聚类精度，符合2.2节中的分析。

图4为GMACO、SMACC、ILFACC、WGACO在各数据集上独立运行20次后运行时间和ARI标准差的折线图表示。从折线图上可以直观地观察到，WGACO在低维数据集上运行时间的稳定性比其余三种算法强，在高维数据集上聚类精度的稳定性比其余三种算法强，符合2.2节中的分析。

4.4 算法统计测试

为了更直观地对比不同算法之间的性能，对GMACO、SMACC、ILFACC、WGACO的运行时间和ARI使用Friedman和Nemenyi后续检验，α设置为0.05。Friedman检验是利用秩实现对多个总体分布是否存在显著差异的非参数检验方法。图5为各算法用Friedman检验图表示的检测结果，图中横轴为算法排序值，纵轴为算法，横线的中点为算法平均序值，若两条横线有交叉，说明对应的算法之间没有明显性能差异。从测试结果可以直观地发现，WGACO的聚类效果和算法效率都明显优于GMACO，比SMACC、ILFACC表现更好。

4.5 算法应用

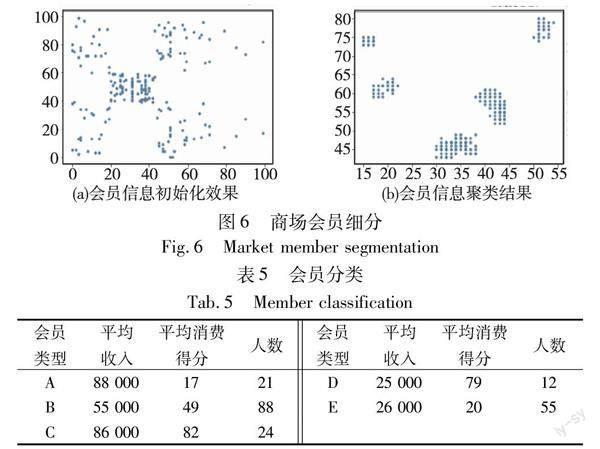
为了验证WGACO的实用性，将其用于商场用户细分，用于给营销团队的决策提供依据。mall customer segmentation data数据集是Kaggle中的商场会员信息，数据集中有200个会员信息，会员信息分别为顾客ID、性别、年龄、年收入和消费得分。由于真实的数据没有标签，所以用轮廓系数作为用户细分结果的评价指标，轮廓系数为［-1，1］，值越大代表聚类效果越好。轮廓系数通过同一簇内数据的内聚程度和不同簇内数据的离散程度对聚类结果进行评价。

图6分别是WGACO对该数据集的初始化效果和聚类结果，聚类结果的轮廓系数为0.62。表5中根据每一类会员的均值收入和消费水平将会员分为了五类，如表5所示。其中：A类会员为高收入低消费客户；B类会员为平均收入和平均消费的客户；C类会员为高收入高消费客户；D类会员为低收入高消费客户；E类会员为低收入低消费客户。不同类型的会员之间的平均收入和平均消费得分有明显的区别，聚类结果的轮廓系数较高，都体现了WGACO聚类结果的合理性，证明了WGACO的应用价值。

5 结束语

本文从LF算法运行时间过长、聚类效果不稳定的问题出发，提出了一种基于熵权的全局LF蚁群聚类算法（WGACO）。WGACO通过信息熵计算数据集各属性权重，并将其加入到欧氏距离的计算当中，随后使用两个权重最大的属性值作为数据对象的初始坐标，同时加入了全局记忆矩阵和算法结束条件。通过在七个UCI数据集和三个人工生成的数据集上的实验，验证了WGACO在聚类精度、算法效率、算法稳定性上都有较好的提升，面对高维数据也有较好的表现。通过在Kaggle用户数据集上的应用，证明了WGACO的应用价值。

但本文算法依赖属性权重，在实验中发现，单一的权重计算方式在面对某些数据集时得出的效果不理想，不过改进后算法的效率有较大的提升，在属性权重确定上多一些时间开销是值得的。因此，后续工作中可以结合多种权重计算方法来保证权重的正确。同时，蚁群算法由于算法参数过多导致实用性较低，减少算法参数也是下一步的研究内容。

参考文献：

［1］Deneubourg J L，Goss S，Franks N，et al.The dynamics of collective sorting robot-like ants and ant-like robots［C］//Proc of the 1st International Conference on Simulation of Adaptive Behavior.1991：356-365.

［2］Lumer E D，Faieta B.Diversity and adaptation in populations of clustering ants［C］//Proc of International Conference on Simulation of Adaptive Behavior.1994：501-508.

［3］刘艳，周斌.增量文本软聚类速度改善算法设计及仿真［J］.计算机仿真，2022，39（8）：524-528.（Liu Yan，Zhou Bin.Design and simulation of incremental text soft clustering speed improvement algorithm［J］.Computer Simulation，2022，39（8）：524-528.）

［4］牛永潔.具有全局指导的启发式蚁群聚类新算法［J］.计算机技术与发展，2013，23（9）：74-77.（Niu Yongjie.A new heuristic ant colony clustering algorithm with global guidance［J］.Computer Technology and Development，2013，23（9）：74-77.）

［5］高阳.一种改进的不平衡数据集过采样方法及其并行算法研究［D］.烟台：烟台大学，2021.（Gao Yang.Research on an improved oversampling method for unbalanced datasets and its parallel algorithm［D］.Yantai：Yantai University，2021.）

［6］王昕宇，罗可.具有全局记忆的LF蚁群聚类算法［J］.计算机工程与应用，2019，55（20）：52-57，113.（Wang Xinyu，Luo Ke.Ant colony clustering algorithm with global memory［J］.Computer Engineering and Application，2019，55（20）：52-57，113.）

［7］沈兴鑫，杨余旺，肖高权，等.基于相似度的蚁群聚类算法［J］.计算机与数字工程，2021，49（6）：1052-1057.（Shen Xingxin，Yang Yuwang，Xiao Gaoquan，et al.Ant colony clustering algorithm based on similarity［J］.Computer and Digital Engineering，2021，49（6）：1052-1057.）

［8］Chen Lianyong，Song Jinyu.Abnormal data detection method based on ant colony clustering［C］//Proc of the 6th International Conference on Electronic Information Technology and Computer Engineering.2022：66-72.

［9］朱峰，陈莉.一种改进的蚁群聚类算法［J］.计算机工程与应用，2010，46（6）：133-135.（Zhu Feng，Chen Li.An improved ant colony clustering algorithm［J］.Computer Engineering and Application，2010，46（6）：133-135.）

［10］刘阳阳，吕伟明，霍萌萌，等.基于LF算法改进的动态蚁群聚类算法［EB/OL］.（2012-04-06）［2023-04-06］.http：//www.paper.edu.cn/releasepaper/content/201204-60.（Liu Yangyang，Lyu Weiming，Huo Mengmeng，et al.Dynamic ant colony clusteralgorithm based on improved LF algorithm［EB/OL］.（2012-04-06）［2023-04-06］.http：//www.paper.edu.cn/releasepaper/content/201204-60.）

［11］甘泉，王慧.一种改进的蚁群聚类分析算法［J］.系统仿真技术，2015，11（3）：219-223，206.（Gan Quan，Wang Hui.An improved ant colony clustering analysis algorithm［J］.System Simulation Technology，2015，11（3）：219-223，206.）

［12］徐晓华，陈崚.一种自适应的蚂蚁聚类算法［J］.软件学报，2006，17（9）：1884-1889.（Xu Xiaohua，Chen Ling.An adaptive ant clustering algorithm［J］.Journal of Software，2006，17（9）：1884-1889.）

［13］Wei Gao.Improved ant colony clustering algorithm and its performance study［M］//Computational Intelligence and Neuroscience.2016：19.

［14］胡健，朱海湾，毛伊敏.基于蚁群聚类的动态加权PPI网络复合物挖掘［J］.计算机应用研究，2020，37（2）：390-397，420.（Hu Jian，Zhu Haiwan，Mao Yimin.Dynamic weighted PPI network complex mining based on ant colony clustering［J］.Application Research of Computers，2020，37（2）：390-397，420.）

［15］胡嘉伟，吴云志，乐毅，等.基于改进LF算法的PPI网络聚类方法［J］.湖南工程学院学报：自然科学版，2016，26（3）：56-59.（Hu Jiawei，Wu Yunzhi，Le Yi， et al. PPI network clustering method based on improved LF algorithm［J］.Journal of Hunan University of Engineering：Natural Science Edition，2016，26（3）：56-59.）

［16］Chniter M，Abid A，Kallel I，et al.Computational complexity analysis of ant colony clustering algorithms：application to students grouping problem［C］//Proc of IEEE International Conference on Systems，Man，and Cybernetics.Piscataway，NJ：IEEE Press，2022：736-741.

［17］Vinh N X，Epps J，Bailey J.Information theoretic measures for cluste-rings comparison：variants，properties，normalization and correction for chance［J］.The Journal of Machine Learning Research，2010，11：2837-2854.

［18］Powers D M W.Evaluation：from precision，recall and F-measure toROC，informed ness，marked ness and correlation［J］.Journal of Machine Learning Technologies，2020（2）：37-63.

收稿日期：2023-02-21；修回日期：2023-04-13

作者簡介：熊伟超（2002-），男，四川南充人，硕士研究生，主要研究方向为数据挖掘、智能计算；蒋瑜（1980-），男（通信作者），四川邻水人，副教授，硕士，主要研究方向为数据挖掘、粗糙集与智能计算（jiangyu@cuit.edu.cn）．