基于可分负载理论的多核密码处理器调度研究
郎俊豪,李伟,陈韬,南龙梅
(战略支援部队信息工程大学,郑州 450000)
0 概述
随着5G 技术、云计算、物联网等迅速发展,海量边缘设备的增加使网络数据量剧增,数据算力需求越来越高。边缘计算是缓解数据中心压力,满足算力需求的重要方式,但由于靠近用户端,其安全问题成为网络安全的关键。密码算法是网络安全的基石,由于边缘设备异构性、实时性等要求[1],以及密码算法的计算密集性,因此设计高能效且同时满足性能与能耗两方面需求的多核密码处理器越来越受到人们的关注。任务调度机制通过分配待处理数据给各个密码处理器核,进而挖掘处理器并行性能潜力,提升计算效能,是高能效多核密码处理器设计的关键。
可分负载理论(Divisible Load Theory,DLT)在过去几十年被广泛应用于并行计算领域[2],提升多核处理器平台的调度性能。DLT 指总任务数据(或称任务负载),可被划分成任意尺寸,且各划分部分数据无依赖关系,可被同时处理,其目标是最小化负载处理时间。视频编解码[3]、大数据科学计算[4]等并行应用中常会基于可分负载理论调度任务数据。对于多核密码处理器,单密码算法的数据相关性较强,为提升多核并行度,大多采用单核实现单算法及大数据量的密码任务处理模式,任务数据可以被任意划分(最小为密码算法单次处理长度)。因此,可分负载理论可应用于多核密码处理器的调度机制研究,基于DLT 分析,确定任务负载传输的时间、数据量大小,实现高能效调度目的。
本文根据多核密码处理器任务负载特征,在给定任务量下以设计高能效的调度机制为目标,利用可分负载理论的分析方法,建立多核密码处理器调度的数学模型。通过分析数学模型,提出多轮与单轮混合任务调度方式,得到优化的任务数据分配轮数、处理器分配任务量等影响多核密码处理器调度效率的关键参数,缩短多核密码处理器总任务调度运算时间,提升负载调度的能效。此外,通过板级测试,验证本文模型的有效性。
1 相关工作
多核处理器负载调度根据负载数据的特征,主要分为基于图的调度和基于可分负载理论的调度。基于图的调度针对任务负载有较强的数据依赖性,将任务表示成任务依赖图(Task Dependency Graphs,TDG)[5-6]以及有向无环图(Directed Acyclic Graph,DAG)[7-8]等图形式,通过分析图来研究多核处理器的调度。基于可分负载理论的调度针对任务数据可任意划分成小单元,划分后数据间无依赖关系,可任意分配到各处理器上。根据多核处理器间通信拓扑关系不同,有研究链式、总线式、单层树状、2D-mesh[9-10]等拓扑结构的调度。根据考虑因素不同,有考虑带前端处理、带结果反馈等因素的调度。
文献[11]以最小化任务处理时间为目标,首次提出可分负载的分析方法,同时考虑通信与计算,研究调度问题,并在形式上给出可分负载理论的最优条件,即所有处理器同时停止运算,但文献只考虑了线性网络拓扑结构,且仅针对传感器网络。文献[12]对可分负载单轮调度方式,在数学上严格证明所有处理器同时停止运算,是可分负载理论达最优处理时间的条件,并给出调度的数学最优解,但研究仍只考虑线性网络拓扑,且单轮调度存在负载不均衡问题。文献[13]基于可分负载理论分析单层树状拓扑结构的多处理器任务调度,并给出各处理器同构情况下的任务负载分配的数学解析解。不同于上述理论研究,文献[14]将可分负载理论应用到并行视频解码中,结果显示采用可分负载理论能有效缩短多核处理器上并行视频解码任务的完成时间。为优化可分负载理论的负载任务完成时间,文献[15]在处理器网络结构参数未知情况下,提出采用自适应负载分配方式,通过探测网络结构分配负载;文献[16]基于可分负载理论分析了当有两个根节点同时调度任务时,多核处理器任务完成时间的变化;文献[17]提出多轮周期调度任务方式,缩短了处理器等待任务传输的时间。文献[18-20]基于可分负载理论分别研究了异构多核处理器实时系统、负载非线性、异构星形拓扑结构上的图像处理任务、雷达图像数据并行处理等不同应用下的负载调度[21]。
针对可分负载理论在单轮调度上存在负载平衡不均、采用多轮调度优化后难以得到解析解、多核处理器研究多为线性拓扑或同构处理器结构、缺乏对异构处理器的分析以及缺乏应用于多核密码处理器调度方面的研究等问题,本文对多核密码处理器的负载调度进行研究,在调度方式上采用多轮与单轮混合方式,多核拓扑结构为单层树状结构,考虑同构、异构情况下的负载调度,建立基于可分负载理论的多核密码处理器调度数学模型,提出高能效的负载调度机制,从数学模型仿真、实际芯片测试两方面对提出的调度策略进行实验分析与评估。
2 多核密码处理器可分负载调度模型
本节基于可分负载理论对单层树状拓扑结构的多核密码处理器进行负载调度研究,建立了单轮调度方式的数学模型,提出多轮与单轮混合调度方式。
2.1 多核密码处理器拓扑结构
调度模型研究的多核密码处理器采用单层树状拓扑结构,如图1 所示。图中负载数据进入调度控制器H0,H0对数据进行调度,依次分配数据到各处理器P1至Pn中,待处理器完成运算后,将结果送到输出控制器H1中输出。在整个多核密码处理器系统中,H0是调度的核心。基于可分负载理论,调度的本质是确定什么时间,输送多少数据量,到哪个处理器Pi(1≤i≤n)。
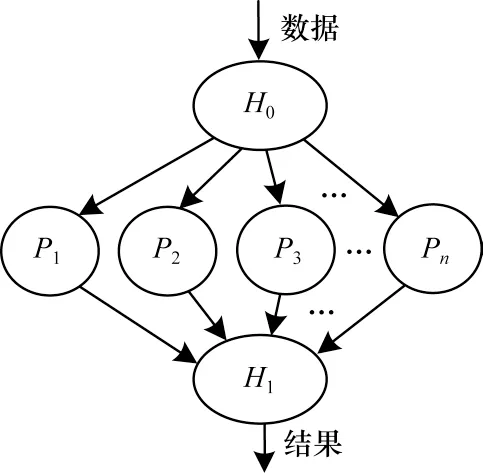
图1 多核密码处理器的单层树状拓扑结构Fig.1 Single layer tree topology structure of multi-core cryptographic processors
高能效的调度方式主要从功耗尽可能低、性能尽可能提高两方面考虑。功耗可以分成静态功耗与动态功耗。对于任务级密码数据处理,一方面,给定任务量条件下,无论采用何种调度方式,需要调度传输的数据量、处理器计算数据量是一定的,因此动态功耗是固定的,而静态功耗与整体数据处理完成时间成正比;另一方面,性能提高要求尽可能减少负载调度、处理完成时间。因此,高能效的调度机制意味着尽可能地减少整个数据的调度计算时间,这与可分负载理论的优化目标,即最小化完成时间是一致的。
2.2 多核密码处理器单轮调度模型
为便于说明,先建立最简单的单轮同构多核密码处理器调度模型。相关参数表示及模型假设如下:
1)处理器拓扑结构为单层树状结构,向量H=(H0,H1)表示输入调度控制器和输出控制器,向量P=(P1,P2,…,Pn)表示各密码处理器核;
2)多核处理器为同构结构,且每个处理器必须接收完全部数据后才开始计算;
3)s表示处理器核运算速度的倒数,c表示数据传输通信速度的倒数;
4)Ts表示单位数据量,是s=1 时的计算时间;Tc表示单位数据量,是c=1 时的通信时间,用于将模型中各变量参数量纲统一到完成时间上;
5)总任务数据量为V,对应占比为1,ai表示分配到处理器Pi的任务占比,有,且0≤ai≤1;
6)Ti表示第i个处理器完成任务负载时间,Tf表示最终任务负载时间。
根据可分负载理论最优条件,当所有密码处理器同时停止运算时,任务负载完成时间最短。若处理器不是在同一时间结束运算,则空闲处理器核可以处理任务,以减少时间,同时之前的研究也给出了最优条件严格的数学证明[12]。根据处理器同时停止的条件,整个调度过程可表示为图2 所示,图中a1×c×Tc表示任务负载a1传输给P1所消耗的时间,a1×s×Ts表示任务负载a1在P1中运算消耗的时间。调度控制器H0给P1传输完负载a1后,P1开始计算,同时H0开始给P2传输负载,依此类推,最终当所有处理器同时停止计算时,整个处理时间最短。

图2 单轮可分负载任务调度Fig.2 Single-round divisible load tasks scheduling
基于已有对可分负载理论分析[13]的研究,当处理器同时停止时达到最优调度,各处理器完成时间如式(1)所示:
又因为同时停止,所以有式(2):
由T1=T2可得a1与a2的关系如式(3)所示:
所以由式(5)及等比数列求和公式,可得式(6):
由式(4)、式(6)可以得到各个处理器调度分配的任务占比如式(7)所示:
其中:当多核处理器结构确定后,r为固定参数,由此可得调度控制器H0的任务调度分配方式,使得当前假设下整个负载处理的完成时间最短,最短时间Tf表达式如式(8)所示:
2.3 多核密码处理器多轮与单轮混合调度模型
第2.2 节基于可分负载理论,在H0的调度控制下得到了数学上的解析最优解,明确给每个密码处理器分配任务负载ai,并得到最优完成时间Tf。但由于假设简单,因此仍存在一些不足,主要有:一是对于处理器Pi来说,i越大(传输数据顺序越靠后),表示需要等待负载的时间越长,这期间存在较多空闲时间;二是单轮分配使得各处理器任务负载不均衡,越靠后的处理器分配到的任务越少;三是第2.2 节的模型是只针对同构情况下的多核处理器;四是未考虑实际情况数据输出的时间消耗。
为进一步优化基于可分负载理论的多核密码处理器调度机制,提升模型的适用性、准确性,减少调度处理时间,在第2 节的基础上优化模型,主要的优化措施有:一是采用多轮与单轮混合调度方式,即第1 阶段采用多轮等量分配方式,以减少处理器空闲等待时间,减少调度处理时间,第2 阶段采用单轮方式,保证所有处理器在相等时间内结束运行;二是考虑异构多核密码处理器情况,引入实际中结果输出耗时参数,精确模型。
为建立优化后的新模型,进一步补充假设如下:
1)总任务分成m轮次,前m-1轮,各不同轮次之间,同一轮调度各密码处理器之间,分配的任务占比相同,即等量,第m轮采用单轮调度分配方式;
2)aij(1≤i≤n,1≤j≤m)表示第j个轮次分配给处理器Pi的任务量
3)si、ci(1≤i≤n)分别表示Pi处理器计算速度、通信速度的倒数;Ts、Tc仍表示单位数据量,当si=1,ci=1时的计算时间、通信时间,为简化模型,Ts、Tc仍为固定值;
4)结果输出时间固定表示为aij×Tout(1≤i≤n,1≤j≤m);
5)处理器Pi输出结果的时间消耗为Toi(1≤i≤n),采用单轮调度的处理器Pi消耗的时间为Tim(1≤i≤n)。
对于多轮任务负载调度,不同轮次、同一轮次内不同处理器调度分配任务的等量或不等量,没有本质上的区别,目的都是为缩短各个处理器等待数据通信时间,尽快进入计算阶段,以得到最佳的传输、计算总时间。在理想情况下,对多核密码处理器,最优的情况是所有处理器能同时处于计算状态。但因运算数据需要传输时间,因此最佳情况变成每个处理器只需要等待自身任务数据传输时间,不受其他处理器影响,且应尽早开始进行运算。因此为便于模型分析,且不失一般性,本文采用不同轮次、同轮次内不同处理器等量任务数据调度方式,且最后一轮次采用单轮非等量调度方式,保证可分负载理论的最优条件,即各处理器同时结束运算。
多轮加单轮混合调度方式过程如图3 所示。整个调度分配分成多轮等量调度、单轮调度两个阶段。对于单轮调度,可用第2.2 节的模型进行分析,得到具体每个处理器需要的任务量。对于多轮等量调度,不失一般性地分析第1 轮次,由于各处理器任务量相等,关键在于分配任务量ai1(1≤i≤n),即最后一个处理器Pn何时开始计算。在图3中,Pn在P1刚好计算完成后开始计算,记该时刻为tp。若实际Pn在tp时刻后,则会增加传输通信消耗时间,Tf无法达到最优;若实际Pn在tp时刻前,则任务传输通信时间较短,但下一轮次仍要等P1运算结果后才能进行运算,对Tf无更多的增益。因此,在多轮等量调度阶段,使Pn在P1刚好计算完成后开始计算,即满足等式,这也便于模型的分析。由可分负载理论的处理器同时结束条件,多轮加单轮混合调度方式完成时间如式(9)所示:
其中:Tim和Toi(1≤i≤n)可表示如式(10)、式(11)所示,分析结果输出消耗时间Toi,从图3 中可以看到,在多轮等量调度阶段,只要结果输出时间小于任务数据调度时间,就可以不考虑,实际上对于密码处理器,结果输出时间不会超过任务数据调度时间,因此可以忽略,所以式(10)只计算了最后单轮阶段的结果输出时间。
根据可分负载的处理器同时停止运算时为最优条件,式(2)的递推等式对多轮等量加单轮混合调度方式依旧适用。等量分配m个轮次,类似的有这两个等式成立。对于异构多核处理器平台,由于si、ci不同,要想直接求解每个任务数据占比aij(1≤i≤n,1≤j≤m)已经被证明是一个NP 困难问题[22-24]。
为分析多轮等量加单轮混合调度的情况,首先考虑当多核密码处理器为同构平台,即计算速度与通信速度均相等时,可得到式(12)~式(14):
其中:式(12)表示考虑同构情况下各处理器核计算、通信速度相等;式(13)表示在多轮等量调度阶段,任务数据占比主要与分配轮次m和处理器数n相关;式(14)则表示第m轮采用单轮调度时,各处理器分配得到的任务量,与式(7)结果类似,只是此处不是对全体任务分配,而是对1/m的任务调度分配。
由式(2)和式(9)~式(14)可得到最终调度,计算完成总时间Tf如式(15)所示:
从式(15)中可以看到,总消耗时间Tf与电路固定参数、处理器核数n、多轮分轮数m有关,在一个固定多核密码处理器平台上,分轮数m是一个变化量,也是调度中的关键。因为r×s×Ts=c×Tc+s×Ts,对式(15)中的项,由于实际结果输出时间要远小于通信加运算时间,因此该项可近似为1,由此对式(15),固定n,对m求偏导数可得式(16):
易证,当n≥1、r≥1时恒成立,则小于0,即Tf对于m单调递减,分的轮次越大,消耗总时间Tf越小。而对于密码算法,由于单个核心处理数据量有最小限制,因此当多轮调度采用每轮次分配最小限制量时,m最大,此时Tf最小,调度方式对多核密码处理器平台为能效最优。
当多核密码处理器平台为异构时,假设通信速度相等,在不同轮次仍采用等量分配方式,在同一轮次中根据不同处理器的计算能力进行比例分配,即,由此可以进行与同构情况下相同的分析。对于第m轮次,即采用单轮方式阶段,代入不同计算速度si,通过解线性方程的方式可以得到相应的调度任务数据负载aim(1≤i≤n)的解。
3 实验结果与分析
为验证本文提出的多核密码处理器调度机制的可行性,分别进行MATLAB 软件仿真实验、多核密码处理器芯片板级任务调度测试并分析结果。
3.1 结果分析
3.1.1 单轮调度仿真分析
通过MATLAB 仿真,使r取不同值,得到如图4所示的多核密码处理器单轮调度时处理器核数与最终完成时间之间的关系。由图4 可以看到,以r=1.1时为例,整个曲线最开始快速下降,之后下降趋势逐渐缓慢,最终趋于不变。这是因为对于多核密码处理器,当任务量固定时,初始提升核心数能有效提升任务处理的并行性,从而完成时间迅速减小;但当处理器核数过多时,并行度提升达到极限,同时核心数增多导致任务传输通信时间增加,即处理器等待任务时间增加,因此完成时间Tf减小的斜率将逐渐放缓,直至趋于不变。
当变化r值时,从图4 中可以看到随着r的增大,各曲线达到极限Tf值时对应的n值越来越小,且趋于不变时的Tf值越来越大。这是因为即代表多核密码处理器通信时间与计算时间的占比,当r趋近于1时,表示计算时间占比更大,通信时间几乎可以忽略,因此随处理器核数n增大导致的通信时间消耗影响会更小,即完成时间Tf所能达到的极限值会更小;当r越大,即通信时间占比增加(如r=2时,表示完成任务需要的数据通信传输时间与计算时间各占总时间的50%),处理器核数n增大导致的通信时间消耗影响加剧,完成时间Tf能达到的最小值增大,即有更多时间浪费在数据传输通信上,需要更长的Tf完成时间。这说明对于单轮调度,处理密码任务的处理器核数、任务本身通信/计算比例两个因素会影响整个调度过程。
除分析调度完成时间Tf的变化趋势及指导调度方式设计外,基于可分负载理论模型还能给出具体的调度策略。以n=4,r=1.1 为例,这表明多核密码处理器有4 个核心,总任务负载的通信/计算占比r=1.1,可得调度方式如表1 所示,最佳调度为分别给处理器P1、P2、P3、P4按序分配如表1 所示比例的任务数据,能达到最优的总完成时间,即达到高能效的调度。

表1 基于可分负载理论的单轮调度示例Table 1 Example of single round scheduling based on divisible load theory %
3.1.2 多轮与单轮混合调度仿真分析
利用MATLAB 对建立的基于可分负载理论多轮与单轮混合调度的模型进行仿真。分别固定m,改变参数r、n;固定n,改变参数r、m;固定r,改变参数m、n;固定m、n、r,变化结果输出因子Tout4种不同情况仿真,从多个维度对多轮与单轮混合调度机制进行分析。
当固定混合调度的轮次m=4时,完成时间Tf随处理器核数增加的变化趋势如图5 所示。对比图4可知,图5 的5 种不同r取值下的完成时间Tf均要小于图4,这表明提出的多轮加单轮混合调度机制在理论上要优于单轮调度方式,即能使得整个任务完成时间更短。这是因为通过划分多轮,能让各个处理器更早地开始运算,减小了负载传输等待时间。从图5 中可以看到,相较于图4、图5 的5 条曲线,当Tf达到极限最小值且趋于平滑时,5 条曲线之间的差值要远小于图4 中该情况下5 条曲线的差值。这是因为采用混合调度方式,分轮次会使得单次传输的任务量减小,即使传输通信速度差异较大,但由于单次传输的任务量小,体现出来的时间差异也相应减小,相当于削弱了通信计算比例参数r的影响。这也侧面说明多轮与单轮混合调度能通过削弱任务传输通信时间消耗影响,提高整个调度的能效。
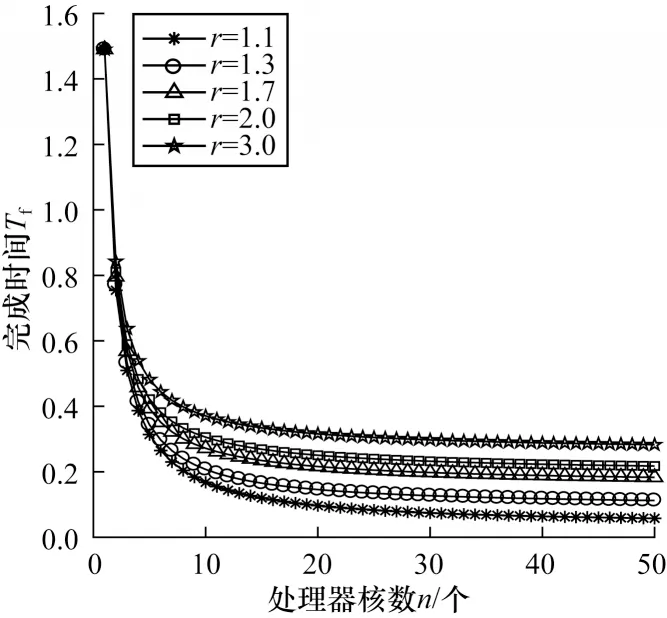
图5 固定轮次条件下混合调度完成时间的变化趋势Fig.5 Changing trend of completion time of mixed scheduling under fixed turns condition
除分析趋势外,建立的模型仍可以得到具体的调度分配方式,以n=4,m=4,r=1.1 为例,为达到最佳总完成时间,调度方式如表2 所示。

表2 基于可分负载理论的混合调度示例Table 2 Mixed scheduling example based on divisible load theory %
当固定混合调度的处理器数n=4时,完成时间Tf随处理器核数增加的变化趋势如图6 所示。由图6可知,当参数r取值不同时,Tf在m=1 处的值也不同,且r越大,Tf值越小。这是因为m=1 表示单轮调度,不划分轮次,因此任务总完成时间Tf值受r影响,这个结论也与图4 的结果相一致。同时可以看到,当m越大时,Tf值越小,且最终趋于相同。这是因为理论上,若m值无限增大,即任务负载可被无限分割小,此时任务传输通信时间就可以忽略,即表现为即使r值差距很大,但图6 中的Tf值最终也趋于相同。当然,在实际中,对于多核密码处理器,每个核有最小处理数据位宽(如AES 算法,其最小处理位宽为128 bit),因此m不可能无限增大,但模型仿真结果暗示了,当m达到单个核可以处理的最小位宽时,本文提出的多轮与单轮混合策略能达到最优的Tf值,这也验证了前述数学求导证明的正确性。

图6 固定处理器数条件下混合调度完成时间的变化趋势Fig.6 Changing trend of completion time of mixed scheduling under fixed number of processors condition
当固定混合调度的通信计算占比参数r=1.1时,完成时间Tf随处理器核数增加的变化趋势如图7 所示。图7 的变化趋势表明,当m、n同时变化时,其与Tf组成的二元函数Tf(m,n)的变化趋势是图5、图6变化趋势的线性结合,即使m、n同时变化,前述的变化规律也仍旧适应,即m越大,n越大,在一定范围内Tf值会迅速减小,但减小的速度会逐渐降低,直至趋于平缓。
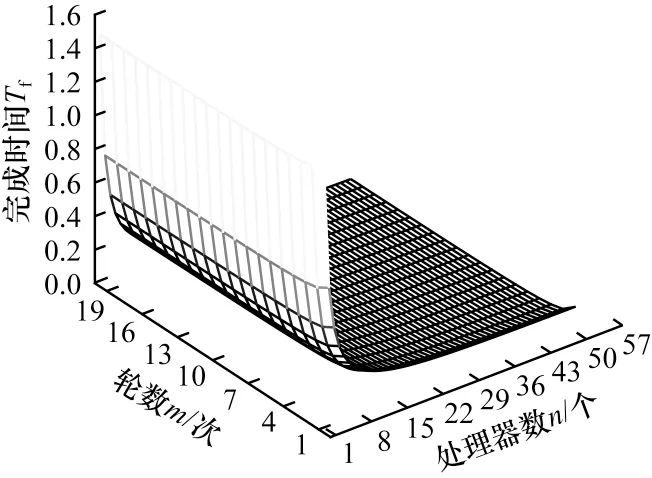
图7 固定参数r 条件下混合调度完成时间的变化趋势Fig.7 Changing trend of completion time of mixed scheduling under fixed parameter r condition
为研究本文模型中结果输出参数Tout对总完成时间Tf的影响,改变Tout的取值,通过MATLAB 仿真得到如图8 所示的变化趋势图。图8 为取处理器核数n=4,轮次m=4,通信计算占比r=1.1 情况下,对应不同Tout值的变化曲线。从图8 中可以看到,随着Tout值的增大,最终完成时间Tf也会增大,但增大的幅度较小。这表明输出Tout值会影响任务总完成时间,同时也说明,结果输出时间的影响占比不大,不是整个混合调度完成时间Tf的主要影响因素,通过调节通信计算占比及合理选择轮次m,可以有效减小结果输出消耗时间的影响。
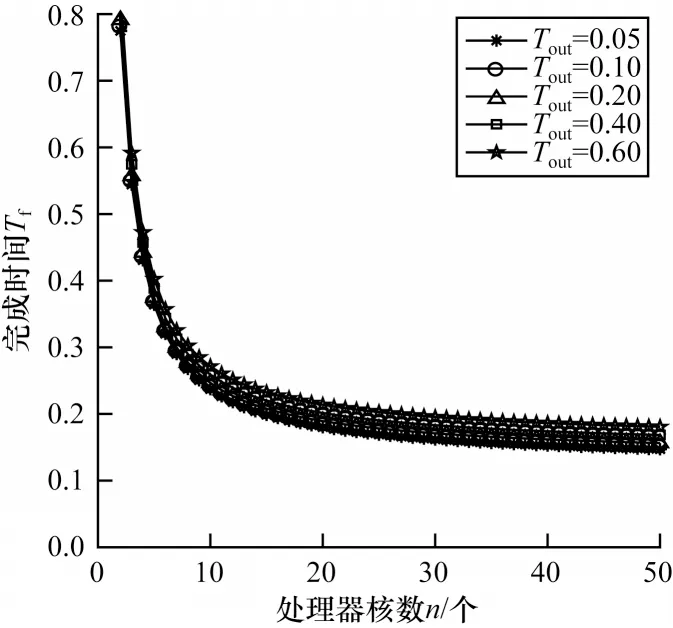
图8 处理器核数与混合调度完成时间的关系Fig.8 Relationshtp between the number of processor cores and completion time of mixed scheduling
3.2 板级测试结果与分析
在现有多核密码处理器芯片的基础上,通过控制输入微控制器采用提出的混合调度方式进行任务负载的调度,验证基于可分负载理论的多轮与单轮混合调度方式的实际有效性。
多核密码处理器芯片的示意结构如图9 所示,处理器由输入微控制器、输出微控制器及4 个密码处理器核组成,4 个密码处理器可以独立工作,也可相互通信。输入微控制器可以进行微代码编程,控制任务负载送到各个密码处理器核心的数量与顺序。多核密码处理器芯片板级测试平台如图10 所示,测试板与ZYNQ 系列FPGA 连接,负责发送数据给多核密码处理器芯片,多核密码处理器中的输入微控制器再进行接收数据的调度,本文考虑的调度是指进入多核密码处理器芯片内任务负载分配给各个核心的调度。

图9 多核密码处理器芯片的结构Fig.9 Structure of multi-core cryptoprocessor chip

图10 多核密码处理器芯片板级测试平台Fig.10 Chip board testing platform for multi-core cryptoprocessor chips
在多核密码处理器板级测试平台上,对密码算法1、算法2、算法3 分别采取任务负载均衡分配调度[25](简称平均调度)、单轮分配调度[10](简称单轮调度)、多轮与单轮混合分配调度(m=1,简称混合调度),3 种方式进行测试,得到任务完成时间Tf的实验结果如图11 所示。算法1、算法2、算法3 的负载任务量均为768×32 Byte,芯片工作频率为256 MHz。由图11 可知,在相同任务量下,算法1、算法2、算法3采用多轮与单轮混合调度方式对比平均调度方式完成时间分别缩短了10.1%、19.1%、48.2%,这说明本文所提出的混合调度方式的有效性。不同算法完成时间的缩短程度不同,与其算法的通信计算时间比有关。注意到平均调度与单轮调度方式差距不大,一方面是因为处理负载任务量不够大,另一方面是因为3 个算法整体来说通信时间占比较小,所以体现不出基于可分负载理论的单轮调度的优势。

图11 不同调度方式下完成时间的对比Fig.11 Comparison of completion time under different scheduling patterns
图12 为算法2 在板级测试时采用不同的轮次m得到的吞吐率变化趋势,当m分别为1、4、8、16时,得到的吞吐率分别为682、812、838、839 Mb/s。可以看到在数据量一定的条件下,随着m值的增大,完成时间Tf不断减少,进而吞吐率增大,但当m足够大时,曲线趋于平缓,这与图6 的仿真结果相一致。

图12 算法2 在不同轮次条件下的吞吐率Fig.12 Throughput rate of algorithm 2 under different turns condition
实际上,当处理数据量固定时,随着m变化,能耗不增加,性能提升,即能效值会相应增大。表3 为在多核密码处理器上使用不同调度方式时得到的板级测试能效值。从表3 可以看到,对于不同算法,对比平均调度和单轮调度方式,本文提出的混合调度方式在能效值上的提升分别为9.8%、18.7%、48.1%,由于不同算法在多核密码处理器上调度时的通信计算比不同,因此提升幅度也有差异。

表3 不同算法的能效值比较Table 3 Comparison for energy-efficiency of different algorithms 单位:(Mb·s-1·mW-1)
4 结束语
针对5G、物联网等背景下边缘设备面临的安全与资源受限等问题对高能效多核密码处理器设计提出的需求,本文提出基于可分负载理论的高能效调度机制。利用可分负载理论的分析方法,建立多核密码处理器上任务负载调度处理数学模型,并提出多轮与单轮混合调度方式。通过MATLAB 仿真分析得到处理器核数、多轮分配轮次、结果输出消耗等因素对多核密码处理器任务完成时间的影响。多核密码处理器芯片板级测试结果表明,本文提出的多轮与单轮混合调度方式能够有效缩短密码任务处理完成的时间,提升多核密码处理器的能效。下一步将继续利用可分负载理论,研究面向异构多核密码处理器平台的高能效负载调度机制,并将单层树状拓扑结构扩展到多层树状拓扑结构,实现更多处理器核数场景下的高能效异构多核密码处理器负载调度。

