基于联合熵的多视图集成聚类分析

赵晓杰，牛雪莹，张继福

（太原科技大学 计算机科学与技术学院，太原 030024）

0 概述

多视图聚类是将给定的多视图数据依据相似性划分为不同的簇，使得相同簇中的对象尽量相似，不同簇中的对象尽量不同［1］。多视图数据可以使得问题描述的角度更全面，提供比传统单视图数据更丰富的信息来揭示其内在结构，并已成功应用于社交网络［2-3］、多模态生物特征分析等领域［4-5］。多视图集成聚类作为一类典型多视图聚类分析方法，通过集成聚类的思想使多个视图较弱的基本分区集成为一个较强的一致分区，并利用多个独立的基聚类器分别对原始数据集进行聚类，然后使用某种集成策略获得最终的聚类结果，其关键在于从特征融合转移到分区融合，相较于特征融合更有利于单视图高层信息的保持。但如何充分利用多视图数据的一致性和互补性，是改善并提升多视图集成聚类效果的关键。

分区融合策略是多视图集成聚类的关键步骤之一，可分为视图加权和簇加权两种。视图加权［6-7］主要是根据每个视图的基聚类损失来确定每个视图的权重，并将每个视图视为一个整体，同一视图中的基聚类簇被赋予相同的权重，而簇加权是根据每个视图分区中基聚类簇的质量来确定权重的。簇加权可比视图加权获得更加详细和灵活的信息，更有利于融合多视图分区。目前，簇加权［8］主要采用基聚类簇内最小平均距离，更加紧密的、数据对象之间距离更小的簇被赋予高权重，稀疏的簇被赋予低权重。基聚类簇的疏密程度仅能体现数据本身分布特性，并不能反映簇质量优劣，即基于最小平均距离的簇评价标准并不能很好地表示聚类质量优劣。本文采用联合熵估计多视图聚类簇的不确定性，提出一种基于联合熵的多视图集成聚类算法。联合熵体现了多视图中所有基聚类簇的数据分布特征，保留了基聚类簇加权优势，体现了不同视图相似对象构成的对应类簇存在差异性，有效地提升了多视图集成聚类效果。本文设计基于联合熵的基聚类簇质量评估方法，构造基于基聚类簇质量评估的加权共协矩阵，提出基于联合熵的多视图集成聚类算法（Multi-View Ensemble Clustering algorithm based on Joint Entropy，MVECJE）。

1 相关工作

多视图聚类综合了数据的多个视图信息，获得了优于单视图聚类的性能，已成为一个研究热点［9-11］。多视图聚类按照视图的融合方式主要分为基于特征融合的多视图聚类［12-15］和基于集成的多视图聚类［16-19］两大类。

基于特征融合的多视图聚类分析的基本思想是将多视图数据的多种特征表示融合成为一个单一表示，并应用传统的聚类分析实现聚类分析任务，同时该类方法在聚类结果的解释方面具有一定优势。典型的研究工作主要包括：文献［20］利用正则相关分析的方法从多个视图的特征中选取相关度最高的视图，以此作为数据融合后的唯一表示；文献［21］利用谱聚类将数据在每种视图下都表示成一个图，并为每个图赋以权重，并用随机游走的方法进行融合形成数据的唯一表示；文献［22］提出一种多核K-means 算法来组合多视图数据，并将此组合作为数据的最终表示；文献［23］用一种核的方法给各视图自适应地赋予权重，之后将这些加权的视图融合为一个最终的表示。这类方法融合后的表示具有可解释性强的特点，但大多依赖于融合前图的初始化，而初始化图的质量通常难以得到保障。

基于集成的多视图聚类分析融合各个视图的聚类结果。与特征融合不同，它们会保持数据的原始表示［24］。但在多视图数据中，低质量视图可能会影响最终的聚类性能，所以，在融合过程中不能平等地对待所有视图的聚类结果。为了确定不同视图对于最终聚类结果的贡献，研究者提出了许多视图加权的多视图聚类方法：文献［17］给每个视图赋一个权重并给出一个超参数对权重进行约束；文献［25］通过一个自加权的方法来给视图自动赋权重，并且不需要额外的超参数。一般来说，大多数现有的视图加权方法根据每个视图的聚类损失来确定每个视图的权重，以使损失较低的视图具有较高的权重。但一个低损失的视图不能保证其内部的簇就一定具有高质量，因为视图加权是针对每个视图整体的加权，视图内部簇的质量好坏并不能在视图权重上得到体现。所以，通过将每个视图作为一个整体来粗略地分配权重，并不能反映一个视图中各个簇的重要性。针对视图加权的问题，一些研究者提出了基于距离对簇加权的多视图聚类方法。这类方法虽然改进了视图加权的方法，研究核心从视图层面转移到了簇层面，但以距离衡量簇内相似度的加权方式并不完善。因为视角的不同，簇的相似度是存在差异的，但不同视图中对应簇的点是一样的，在这种情况下，不同视图下同样点构成的簇由于相似度的不同，被赋予了不同的权重，不利于得到有效的相似度矩阵。

综上所述，基于特征融合的多视图聚类分析方法太过依赖初始图的质量，基于集成的多视图聚类分析方法则容易忽略视图内部基聚类簇的质量，从而影响视图内部基聚类簇局部特性的体现。

2 关键视图与联合熵

在多视图聚类中，如何处理少数关键视图是关键和核心，影响着多视图聚类性能。文献［6］通过折中稀疏权重与平均权重调整各视图权重，从而保证了少数关键视图信息，其基本概念描述如下：

假设一个多视图数据集由V个视图组成，每个视图有N个实例，由表示，其中，表示来自第v个视图的第i个实例，d(v)表示第v个视图的特征维数。视图中的实例在高维映射下可以表示为，这些实例将会被分成M个不相交的基聚类簇，其目标函数可表示为：

在式（1）中，当p→1时，仅选择一个最佳视图，而当p→∞时，每个视图上权重ωv趋于相等。为了评判关键视图，在聚类过程中嵌入一种核方法对多视图重要性自动排序；然后，根据视图排序对视图赋予权重，这样就在稀疏权重与平均权重之间进行了折中，从而避免了视图赋权中极端情况的产生。尽管视图权重体现了视图整体的重要性，但视图内部基聚类簇的重要性并未得到体现。

采用传统聚类算法，在给定的输入参数下，生成的若干类簇称之为基聚类，基聚类中的每一个类簇称之为基聚类簇，基聚类簇是由相似数据对象构成的一个数据子集［26］。为了使视图内部基聚类簇的重要性得以体现，首先按照选取的聚类算法，按不同参数运行M次，生成M个基聚类，且每个基聚类中包含了若干基聚类簇。在基聚类的生成过程中，尽管选用了同一聚类算法在不同参数下产生基聚类，但在选择聚类算法时，尽量选取输入参数少，且在不同输入参数下生成不同基聚类的算法，从而保证基聚类的多样性。

MVKKM 是一种多核K-means 聚类算法［6］，仅有聚类个数k和视图权重约束p两个输入参数，相比其他聚类算法，MVKKM 输入参数少，且在不同参数下生成的聚类簇也不尽相同，从而保证了基聚类的多样性。假定数据集O={o1，o2，…，oN}，其中，oi是第i个数据对象，N是数据集O中数据对象的个数。采用MVKKM 算法并选用M个不同参数对数据集O进行聚类，生成M个基聚类，每个基聚类由一定数量的基聚类簇组成。M个基聚类的集合表示如下：

其中：Π表示所有基聚类的集合；π（m）表示第m个基聚类中包含的n（m）个基聚类簇；表示π（m）中第n（m）个基聚类簇。

为了便于表示与计算，将所有基聚类中的基聚类簇表示为如下集合：

其中：Ci表示第i个基聚类簇；nc表示Π中所有基聚类簇的个数。

基聚类的形式化表示如下：

其中：π表示基聚类；p为参数，不同的p产生不同的基聚类π。

联合熵是信息熵的推广，用于对与一组随机变量相关的不确定性进行度量，并具有以下特性：1）非负性，即一组随机变量的联合熵是一个非负数；2）高值性，即一组变量的联合熵大于或等于该组变量的所有单个熵的最大值；3）低值性，即一组变量的联合熵小于或等于该组变量各个熵的总和。相关概念定义如下：

对于一对离散随机变量(X，Y)，联合熵H(X，Y)定义如下：

其中：x和y分别是X和Y的特定值；p(x，y)是这些值产生交集时的联合概率。

当且仅当随机变量X和Y相互独立时，则认为H(X，Y)=H(X)+H(Y)。因此，给定n个独立的随机变量X1，X2，…，Xn时，有：

3 多视图集成聚类

3.1 基聚类簇质量评估

视图权重主要针对分布稀疏性，只能体现视图整体的重要性，并不能体现视图内部基聚类簇的重要性，影响了多视图聚类效果。为了使视图内部基聚类簇的重要性得以体现，对由式（3）得到的基聚类簇集合中的每个簇进行不确定性分析。由式（5）可知，联合熵度量了一组随机变量的不确定性，而基聚类簇中的数据对象可看作一组随机变量，因而联合熵可有效刻画基聚类簇的不确定性［26］。

对于由式（2）得到的基聚类集合Π，参照式（5），式（3）中的基聚类簇Ci相对于基聚类π(m)∈Π的不确定性描述如下：

由式（8）可知，对于任意的i、j和m，都有p(Ci，∈[0，1]，因而H(m)(Ci)∈［0，+∞）。当基聚类簇Ci中的所有数据对象都属于π(m)中的同一基聚类簇时，Ci对π(m)的不确定性达到最小，即0；当基聚类簇Ci中的数据对象属于π（m）中更多不同的基聚类簇时，Ci相对于π(m)的不确定性就会变大，表明Ci中的数据对象相对于π(m)不会出现在同一基聚类簇中。

对于任意的基聚类簇Ci，参照式（6），基聚类簇Ci对于基聚类集合Π的不确定性描述如下：

其中：M表示集合Π中基聚类的个数。

由式（9）可知，任意的基聚类簇Ci在集合Π中的不确定性，都有H(Π)(Ci)∈[0，+∞)。

为了将基聚类簇不确定性取值范围控制在［0，1］之间，可采用指数函数对基聚类簇不确定性进行转换，并将其定义为基聚类簇不确定性指数（Cluster Uncertainty Index，CUI），描述如下：

其中：M表示集合Π中基聚类的个数。

由式（10）可知：当基聚类簇Ci的不确定性为最小值0时，其CUI 值将达到最大值，即1；当基聚类簇Ci的不确定性趋于无穷时，其CUI 值趋近于0。

3.2 加权共协矩阵

共协矩阵描述了在基聚类集合中每一对数据出现在同一基聚类簇的频率，可用来表征基聚类结构。虽然共协矩阵常应用于集成聚类分析中，但由于其平等地对待所有数据对象，因此未能有效地体现基聚类特性，影响了集成聚类性能。由式（10）可知，CUI 刻画了基聚类中基聚类簇的不确定性，并且不同基聚类簇的CUI 值是不同的，因此以CUI 值作为权值，可使基聚类簇重要性得到有效体现。对于给定基聚类集合Π，参照文献［27］共协矩阵的描述，加权共协矩阵定义如下：

在式（11）中，权值是由CUI 值来表征的，体现了基聚类簇重要性，CUI 值越大，基聚类簇越重要，反之亦然。

3.3 基聚类集成

依据式（11）定义的加权共协矩阵，可获得多视图集成聚类的一致划分，并采用自底向上策略实现聚合聚类。假设每个数据对象是一个单独的基聚类簇或区域，初始的N个数据对象视为N个初始区域，基本步骤如下：

2）根据基聚类簇间相似度S（t）将相似度最高的两个区域合并成一个新的区域，并更新区域集。第t步中的区域集合描述如下：

其中：表示R(t)集合中的第i个区域；|R(t)|表示R(t)中的区域个数。

在区域合并后，将根据新的区域集合更新相似度矩阵，为下一次迭代过程做准备，迭代到第t步的相似度矩阵S(t)中的第（i，j）项描述如下：

3）当区域集合中的个数|R(t′)|=k时迭代终止，并将最后的区域集R(t′)作为最终的结果输出。

在上述基聚类集成步骤中，采用联合熵来评估基聚类簇的不确定性，并以CUI 值作为加权共协矩阵中的权值，以此构建新的初始相似度矩阵，体现重要数据对象的地位与作用。

3.4 基于联合熵的多视图集成聚类算法

依据上文所述，利用联合熵，多视图集成聚类分析基本思想为：首先针对各视图数据，采用多核K-means 聚类MVKKM 算法生成基聚类集合；然后利用式（11）得到加权共协矩阵，并作为初始相似度矩阵；最后利用层次聚类思想，自底向上地聚合基聚类簇，进而得到最终的多视图集成聚类簇。算法描述如下：

算法MVECJE

输入多视图数据集，k

输出聚类结果R(t′)（|R(t′)|=k）

1.利用MVKKM 算法生成M个基聚类；

2.由式（9）计算基聚类集合中所有基聚类簇的不确定性；

3.由式（10）计算基聚类集合中所有基聚类簇的CUI 值；

4.由式（11）计算得到WWCA矩阵；

5.初始化相似度矩阵S(0)和区域集合R(0)，|R(0)|=N；

6.While |R(t)|＞k Do（t=1，2，…，N-1）

7.依据S(t-1)将R(t-1)中两个相似度最高区域进行合并；

8.由式（12）、式（13）得到新的R(t)和S(t)；

9.End While

时间复杂度分析如下：MVECJE 算法中的主要操作包括生成基聚类与迭代生成基聚类簇。生成基聚类主要是利用MVKKM 算法，参照文献［6］可知，时间复杂度为O(N2(V+τ)τ′)，其中，N为数据对象的个数，V为视图个数，τ为核K-means 算法的迭代 次数，τ′为整体的迭代次数。生成基聚类簇的过程需要迭代t次，每次迭代后需要更新并保存相似度矩阵，时间复杂度为O(tN2)。因此，MVECJE 算法时间复杂度为

4 实验分析

实验环境：Intel®CoreTMi7-7700HQ CPU@2.80 GHz，8 GB内存，Windows 10。为了验证MVECJE 算法的有效性，采 用NMI、ACC 和ARI 这3 个聚类性能指标［28］，对比算法为CoregSC［29］、AWGL［17］、MMSC［16］、DIMSC［13］、COMVSC［30］、MVKKM［6］和CWK2M［8］。选取4 个广泛使用的多视图数据集进行性能评估，即MSRC-v1、Caltech101-7和Handwritten numerals（HW）3 个图像数据集和1 个Reuters 文本数据集，详见表1，其中括号内的数字是特征维数。

表1 实验数据集Table 1 Experimental datasets

4.1 聚类簇权重

为了进一步验证簇权重在集成过程中的重要性，在MVECJE 算法中，删除簇权重处理步骤，即对基聚类直接进行集成处理，并标记为MVEC_1 算法。对比在4 个数据集上的实验结果，详见表2，其中加粗数据表示最优值，下同。

表2 聚类簇权重对聚类性能的影响Table 2 Effect of cluster weight on clustering performance

由表2 可知，聚类簇权重可以有效改善聚类性能，相对于MVECJE算法，MVEC_1 算法的3个聚类指标值都有不同程度的提高，其主要原因是利用联合熵赋予的聚类簇权重，体现了各多视图聚类簇的重要程度。

4.2 聚合迭代

为了验证MVECJE 算法中聚合迭代次数对聚类性能的影响，以3 个评价指标值作为y轴、以迭代次数作为x轴绘制曲线。在表1 所示的4 个数据集上MVECJE 算法的NMI、ACC、ARI 聚类指标如图1所示。

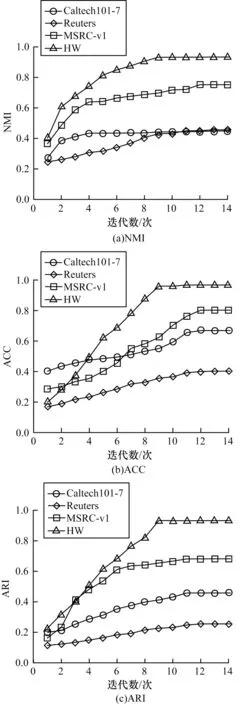
图1 迭代次数对聚类性能的影响Fig.1 Effect of the number of iterations on clustering performance

由图1 可知，随着迭代次数的增加，体现聚类性能的NMI、ACC、ARI 聚类指标值逐步提升，且多视图聚类性能也逐步趋于稳定，其主要原因是在每次聚合迭代集成过程中，根据更新后的相似度矩阵合并了相似度高的聚类簇，随着迭代次数的增加，聚类簇的变化也逐渐变小，并趋于稳定。

4.3 聚类性能

为了验证MVECJE 算法的聚类准确性，对同一数据集使用相同的内核：M=15。对MSRC-v1、Caltech101-7 和HW 数据集使用高斯核，并将标准差设置为每个视图中数据对象之间成对的欧氏距离的中位数，对Reuters 数据集使用线性核。对于MVKKM 和CWK2M，参数p以对数形式进行搜索（lgp从0.1 到2，步长为0.2），而初始中心的选择则通过全局核K-Means 算法来对每个视图进行选择。由于MVKKM 和CWK2M 的中心初始化是相对固定的，因此仅运行1次，其他对比算法则运行30次，并返回30 次结果的平均值。

由表3 可知，MVECJE 算法在4 个数据集上均表现出良好的聚类性能，尤其在Caltech101-7 和HW 数据集上优势最为明显，而在MSRC-v1 和Reuters 数据集上，仅ACC 指标值略逊于CWK2M 算法。具体分析如下：

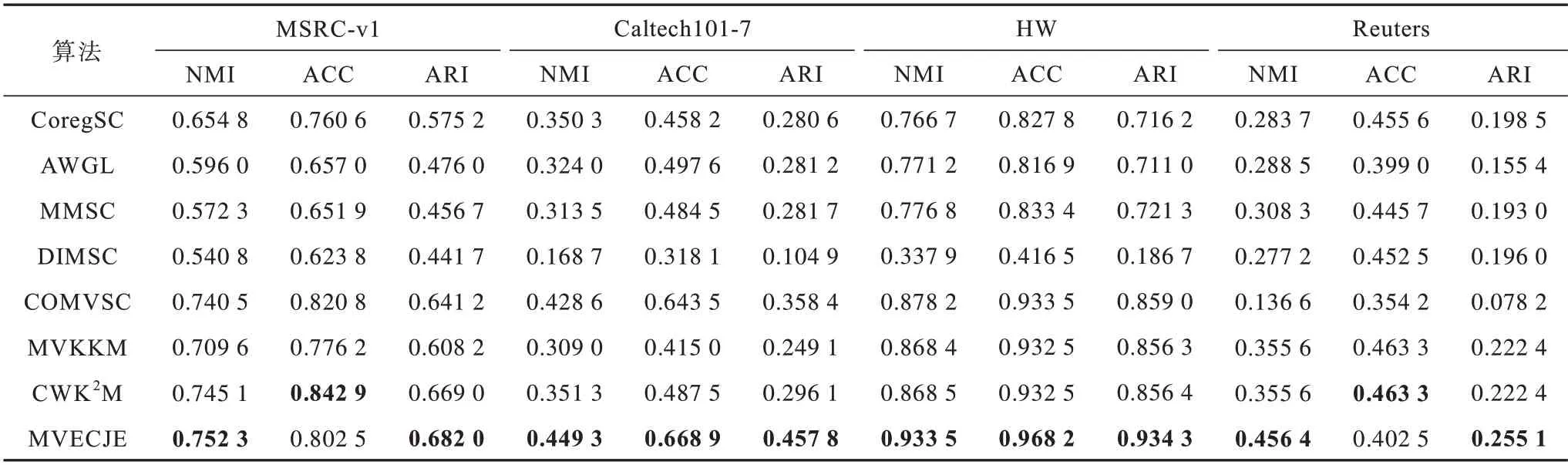
表3 多视图聚类性能对比Table 3 Comparison of multi-view clustering performance

1）MVECJE 是一种集成聚类方法，提高了聚类结果的质量和健壮性，且充分利用了基聚类，并采用了基于联合熵的簇评估方式，使得其具有良好的聚类性能。

2）CoregSC、AWGL 和MMSC 是基于谱聚类的多视图聚类分析方法，聚类性能大多依赖于关联矩阵的构造，但关联矩阵的质量通常是难以保障的，而MVECJE 则不需要构造关联矩阵这一过程，从而也体现了MVECJE 的优越性。

3）DIMSC 和COMVSC 是基于子空间的多视图聚类分析方法，且这两种多视图聚类分析方法都没有进行加权操作，都将每个视图同等对待。因此，视图与视图内部聚类簇的重要性将难以体现，而MVECJE 则是在聚类簇这一层面上进行的分析，从表3 中也可直观看出，MVECJE 相比于DIMSC 和COMVSC 的优势是非常明显的。

4）MVKKM 是一种视图加权的多视图聚类分析方法，而MVECJE 则是以联合熵为基础并对聚类簇加权的多视图集成聚类算法。由于MVECJE 考虑了比MVKKM 更细粒度的权重，因此获得了优于MVKKM 的聚类性能。

5）CWK2M 和MVECJE 都是基于簇加权的多视图聚类分析方法，但对簇加权的方式不同：CWK2M采用欧氏距离为簇加权，MVECJE 对簇联合熵加权。MVECJE 算法在MSRC-v1 和Reuters 数据集上，仅ACC 指标值略逊于CWK2M 算法，这可能是因为数据集对象个数较少，无法有效地体现联合熵加权的有效性。

为了验证MVECJE 算法的聚类效率，采用表1所示的数据集，对不同算法的聚类效率进行对比，如表4 所示。

表4 聚类效率对比Table 4 Comparison of clustering efficiency 单位：s

由表4可知，除CoregSC 效率较高、CWK2M 效率较低以外，包括MVECJE 在内的其他算法聚类效率基本相同，主要原因是：CoregSC 算法通过将各视图的特征向量矩阵正则化为一个共同一致的特征向量矩阵，使得每个视图的特征向量相似，因此无须像其他聚类算法一样将所有视图的特征向量矩阵进行组合；CWK2M 算法采用了一种基于距离的簇加权方法，其簇权重需要重复迭代计算。

5 结束语

本文采用联合熵评估基聚类簇质量，提出一种多视图集成聚类分析方法，有效地刻画了基聚类簇的重要程度与质量优劣，体现了基聚类簇在不同视图中存在差异化的特点，并改善了多视图集成聚类性能。下一步研究工作是针对聚类簇集成，优化其迭代步骤，降低时间复杂度。