双直喷型柴油JCCI 模式的参数优化数值模拟

王 健，礼 博，张 恒，姜龙龙，隆武强，田 华

(1.大连理工大学能源与动力学院，大连 116024；2.哈尔滨工程大学动力与能源工程学院，哈尔滨 150001)

能源安全与环境保护已经成为当今社会的热点话题，针对生态环境的日益恶化，国内外相继颁布了多部较为严苛的排放法规.而随着排放限值的不断降低，尾气后处理装置成本的逐步提高，优化缸内燃烧过程成为降低污染物排放的另一工作重点.

传统柴油机属于扩散燃烧模式，燃烧过程中会同时存在局部过浓区和局部高温区，从而导致大量的碳烟和氮氧化物的产生.为了解决这一问题，胡国栋教授[1-2]正式提出了“柴油机热预混合燃烧”的理念，指出“柴油机在混合气形成和放热规律方面汽油机化”，以此实现稀薄预混合气的多点压缩自燃，在减少污染物的同时提高热效率.

为了进一步提高柴油机预混合压燃模式(premixed charge compression ignition，PCCI)的整体性能，国内外研究者采用了多种技术手段，例如废气再循环技术(exhaust gas recirculation，EGR)[3]、可变气门正时技术(variable valve timing，VVT)[4]、可变压缩比技术(variable compression ratio，VCR)[5]、以及多次喷射[6-7]等.但是柴油的挥发性较差，黏度较高，很难制备高质量的预混合气，且柴油较高的十六烷值导致其面临严峻的早燃问题，燃烧速率过快，限制了PCCI 模式的运行范围.为此，Inagaki 等[8]提出使用进气道喷射异辛烷，结合缸内早喷柴油的双燃料分层PCCI 模式，通过调整两种燃料的比例，控制预混合气的燃烧速率.Kokjohn 等[9]将这种性质不同的双燃料缸内混合的燃烧模式称为活性控制压燃(reactivity controlled compression ignition，RCCI)模式.国内外学者也相继针对双燃料预混合压燃模式开展了大量的研究，并取得了一定的成果[10-11].但是，Wissink等[12]指出，这种进气道喷射制备预混合气的方式THC 和CO 排放较高，且在达到满负荷工况之前，缸内直喷柴油所占的比例已经降低至0，限制了负荷的进一步拓展.Dec 等[13]指出，缸内的分层作用对于控制放热速率、降低压力升高率起到关键作用.为了实现灵活可控的缸内分层，双燃料双直喷策略受到了更多研究者的关注.

Wissink 等[14]通过缸内早喷柴油，压缩上止点附近喷射汽油，实现DDFS(direct dual fuel stratification)燃烧模式，该模式结合了RCCI 模式的高效率和PPC(partially premixed combustion)模式宽负荷范围的优势，同时提高了燃烧稳定性，降低了对EGR 的依赖.Li 等[15]采用数值模拟结合优化算法，针对柴油-甲醇DDFS 模式开展了性能研究，结果表明，相比于RCCI 模式，在低负荷条件下DDFS 模式的热效率更高，THC 和CO 排放量更低.Long 等[16-17]提出了缸内早喷制备灵活可控的预混合气，在压缩上止点附近通过射流引燃预混合气的理念，即射流控制压缩着火(jet controlled compression ignition，JCCI)模式，并基于186FA 发动机平台实现了双直喷柴油JCCI 模式.台架试验结果表明，柴油射流正时可以有效控制预混合气的着火相位，且JCCI 模式具备的两阶段高温放热过程，在拓宽发动机运行范围方面，展现出了极大的潜力.

前期台架试验验证了双直喷型柴油JCCI 模式在燃烧和排放方面的优势，并且得到了主要关于喷射参数的单一影响规律，但是多参数对于双直喷柴油JCCI 模式的综合影响尚不明确，并且台架试验研究效率较低且成本较高，因此以双直喷柴油JCCI 模式为研究对象，通过三维数值模拟的方式，结合简化化学反应机理，以及多参数多目标优化算法，分析双直喷型柴油JCCI 模式的缸内工作特点，全面优化柴油JCCI 模式的性能.

1 计算方法

1.1 三维计算模型

本文计算模型的建立过程包括两部分，首先，建立与台架试验一致的全燃烧室模型并完成计算模型验证，根据双直喷型柴油JCCI 模式台架试验[16]，建立包含余隙在内的等比例扁平型燃烧室几何模型，发动机主要参数如表1 所示.

表1 发动机主要技术参数Tab.1 Main parameters of the engine

计算过程从进气门关闭时刻(-135.5°CA)开始，至排气门开启时刻(124.5°CA)结束，所以计算中的几何模型中不包括进、排气道.参考试验中双直喷喷油器的安装位置、喷雾角度及喷油器参数[16]，设置模型中喷射参数，具体喷射参数如表2 所示，缸内初始条件设置与试验测量结果保持一致.缸内构造及双直喷喷雾示意图如图1 所示，图中左侧所示为-60°CA ATDC 时预喷喷雾的剖面图，右侧所示为-17°CA ATDC 时射流喷喷雾的剖面图.

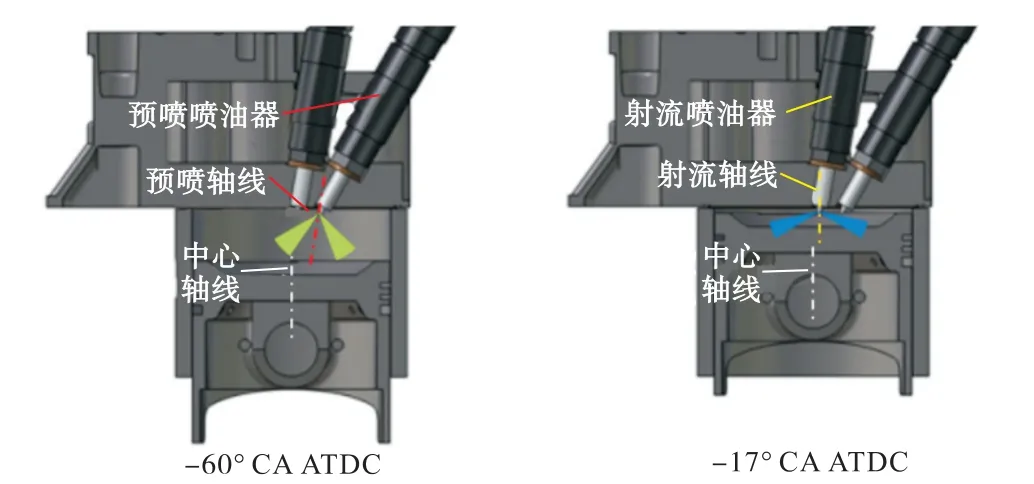
图1 缸内构造及双直喷喷雾示意Fig.1 Schematic diagram of dual-direct injectors

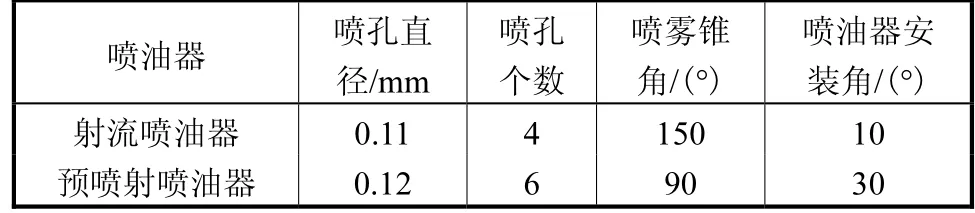
表2 试验用双直喷喷油器参数Tab.2 Parameters of dual-direct injectors

参考Park 等[18]在缸径为82 mm 发动机计算时的边界条件设置壁面初始温度设置如表3 所示.

表3 壁面温度Tab.3 Wall temperature

使用RNG k-ε 模型计算缸内湍流，使用KH-RT模型计算喷雾破碎过程，并以 Peng 等[19]在计算86 mm 发动机时所用参数为依据，对KH-RT 的模型进行设置，油滴蒸发模型使用Frossling 模型，油滴碰撞模型使用NTC collision 模型.考虑到台架试验用所用到的燃料包含柴油和汽油两种组分，因此使用Wang 等[20]的简化化学反应机理.在模拟燃烧时缸内的化学反应时，以正庚烷 nC7H16代表柴油，以异辛烷 iC8H18代表汽油.使用Extended Zeldovich 模型预测缸内 NOx的生成过程，使用Hiroyasu 模型预测发动机燃烧过程中的碳烟排放，以Kong 等[21]的研究结果为依据对模型中的经验常数进行设置.最后，本文以化学反应机理计算的结果确定缸内最终的THC 和CO 排放结果.

1.2 计算模型验证

为了保证模拟的计算精度，本研究利用CONVERGE 软件的自适应网格加密(adaptive mesh refinement，AMR)功能对计算过程进行自适应加密.并且为了节省计算时间，提高计算效率，本研究设置初始计算网格尺寸为2 mm.为了确定建立模型的准确性，分别选择了Lee[22]的PCCI 模式试验结果和前期的JCCI 模式试验结果对燃烧与排放模型进行验证.图2 所示分别为PCCI 模式与JCCI 模式的缸压、放热率以及排放性能等参数的计算结果与试验结果的对比，对比结果显示试验值与计算值的最高燃烧压力误差低于2%，说明所建立的计算模型可以有效地预测发动机缸内工作过程[23].

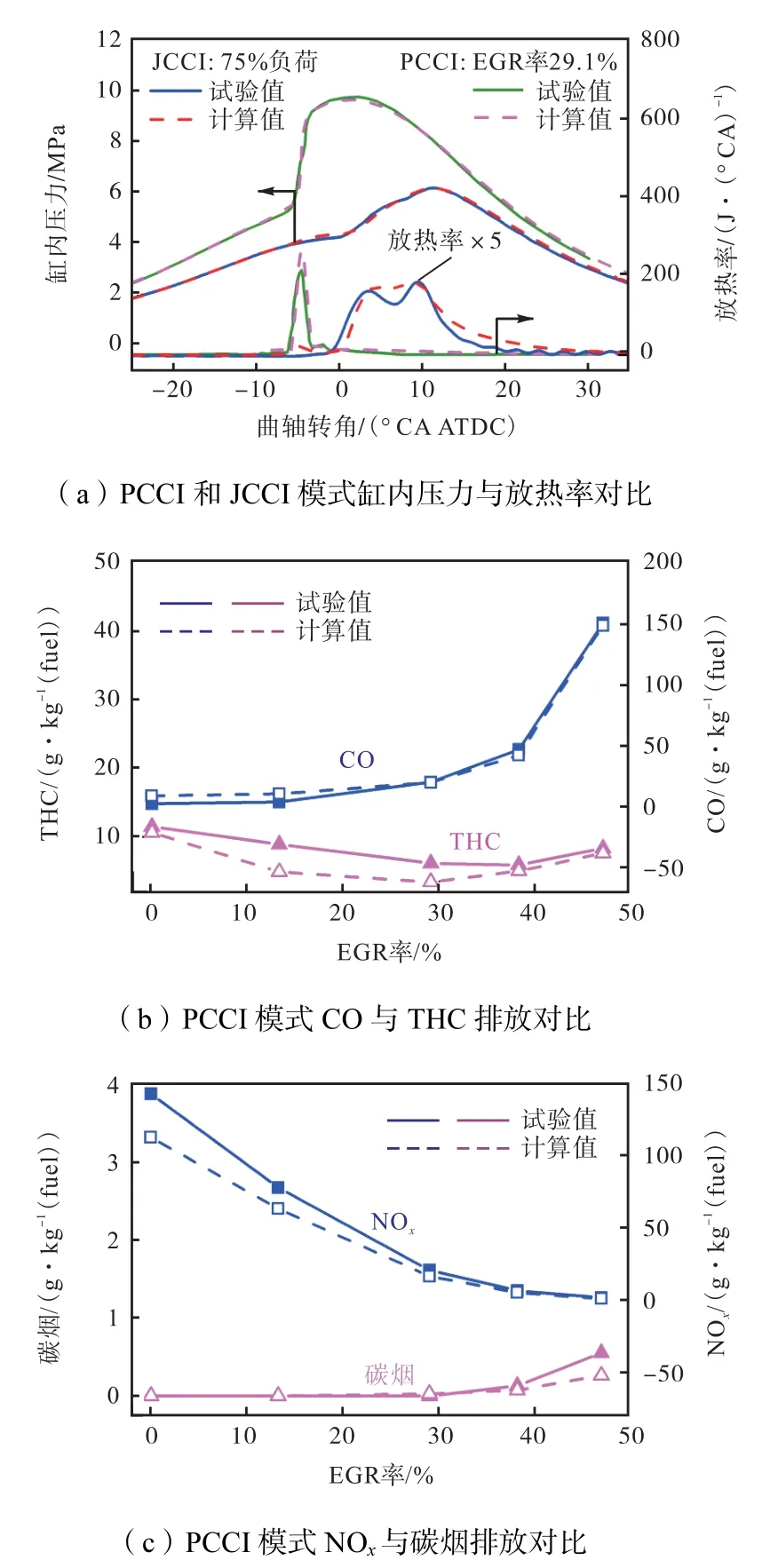
图2 计算结果与试验结果对比Fig.2 mpaison between simulation results and experimental results

为了提高计算效率，采用与Lim 等[24]相同的三维模型简化方法，即假设两个喷油器的喷孔数量相同，均为6 孔.两个喷油器都配置在气缸的中心，两种燃料(预喷射汽油和射流柴油)从相同位置的喷孔喷射，喷雾锥角分别与试验参数保持一致.最后采用六分之一燃烧室模型进行计算，图3 所示为曲轴转角处于-60°CA ATDC 时六分之一简化模型预喷射喷雾与射流喷雾的位置示意图.

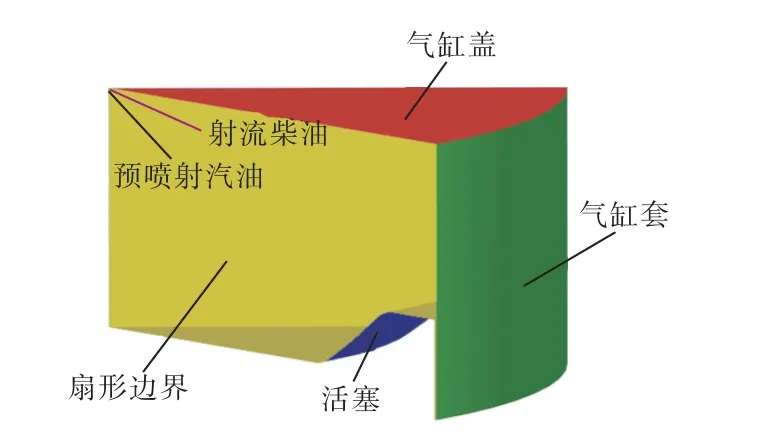
图3 六分之一简化计算模型Fig.3 The one-sixth simplified simulation model

1.3 计算参数定义

由于本文所述发动机使用柴油和汽油两种燃料，因此采用当量燃油消耗率REISFC(equivalent indicated specific fuel consumption)来评价燃油经济性，其计算公式如下：

式中：md和 mg分别为柴油和汽油的质量；QLHV,d和QLHV,g分别为柴油和汽油的低热值；Ef为燃料总能量.

利用声响强度 qRI(ringing intensity)量化压缩点火燃烧中发动机的噪声水平，其计算公式如下：

式中：γ为气体热容之比(cp/cv)；为基于时间的最大压力升高率；pmax为缸内最大压力；R 为气体常数；Tmax为循环过程中气体的最大温度.

文中出现的SOI(start of injection)表示燃油喷射正时，下标pre 和jet 分别表示汽油预喷射和柴油射流喷射，预喷射能量比表示整个循环汽油所含能量与总能量的比值.

定义达到总放热量的 10% 时的曲轴转角为CA 10，表征燃烧起始时刻，达到总放热量的50%时的曲轴转角为CA 50，表征燃烧相位，达到总放热量的90%时的曲轴转角为CA 90，表征燃烧结束时刻.

1.4 优化算法与计算条件

为了协调多参数对发动机性能的影响，全面提升发动机各方面的性能，本文引入CAESES 软件中的NSGA-Ⅱ优化算法，通过Python 脚本搭建三维数值计算和优化算法二者的数据接口，实现双向调用，建立基于多目标优化算法的三维数值模拟平台，并用于本文的计算工作.本文使用的NSGA-Ⅱ算法中，设计了30 代，每一代包含28 个，因此共包含840 个设计算例.

设计算例限制值的设定如下：为了避免发动机敲缸以及降低发动机噪声，缸内最高压力限制在12 MPa 以下，同时因此控制声响强度在5 MW/m2以下；为了避免失火，缸内最高温度的最低值限制在1 100 K 以上；为了模拟EGR，缸内初始O2质量分数设置为 18%；此外，等效燃油消耗率上限设置在230 g/(kW·h)以消除热效率过低的算例.在优化过程中，超过任何一个限制值的个体的都会被舍弃.本次优化中以NOx、EISFC 和碳烟为优化目标对设计算例进行优化，得出可以进一步分析的有效解.

2 计算结果与分析

2.1 设计算例初始参数对燃烧过程的影响

设计算例中所有个体的分布情况如图4 所示.从图中可以看出，随着种群的逐代进化，3 个目标值都逐渐得到了改善，直到最终取得符合限制条件的有效解，初步实现发动机的性能优化.尽管图4 中的A、B 两组解具有较低的当量燃油消耗率，但是不满足其他限制条件而被舍弃，A 组的4 个点均具有较小的预喷射能量比、较低的初始温度以及较高的初始压力，因为最高燃烧压力大于限制条件中的12 MPa而被舍弃；B 组则具有较大的预喷射能量比和较晚的预喷正时，但由于声响强度高于限制条件中的5 MW/m2而被舍弃.

图4 设计算例的所有个体Fig.4 All the calculation results in the optimization process

前期发动机台架试验研究结果表明，柴油射流正时与预喷正时对于双直喷型柴油JCCI 模式的燃烧相位具有显著影响，因此本节对二者与燃烧过程的具体关系进行分析.图5 所示为柴油射流正时对有效解CA 10、CA 50、CA 90 和燃烧持续期(CA 90-CA 10)的影响.可以看出，随着柴油射流正时的推迟，CA 10和CA 50 呈现增加的趋势，CA 90 无明显的趋势变化，进一步验证了柴油射流正时对JCCI 模式CA 10和CA 50 的有效控制作用.且随着柴油射流正时的推迟，燃烧持续期明显缩短，主要是因为推迟柴油射流正时，柴油与空气的混合时间缩短，缸内高活性柴油的局部当量比增加，因此燃烧速率加快，燃烧持续期缩短，这与于超等[25]的研究结论一致.

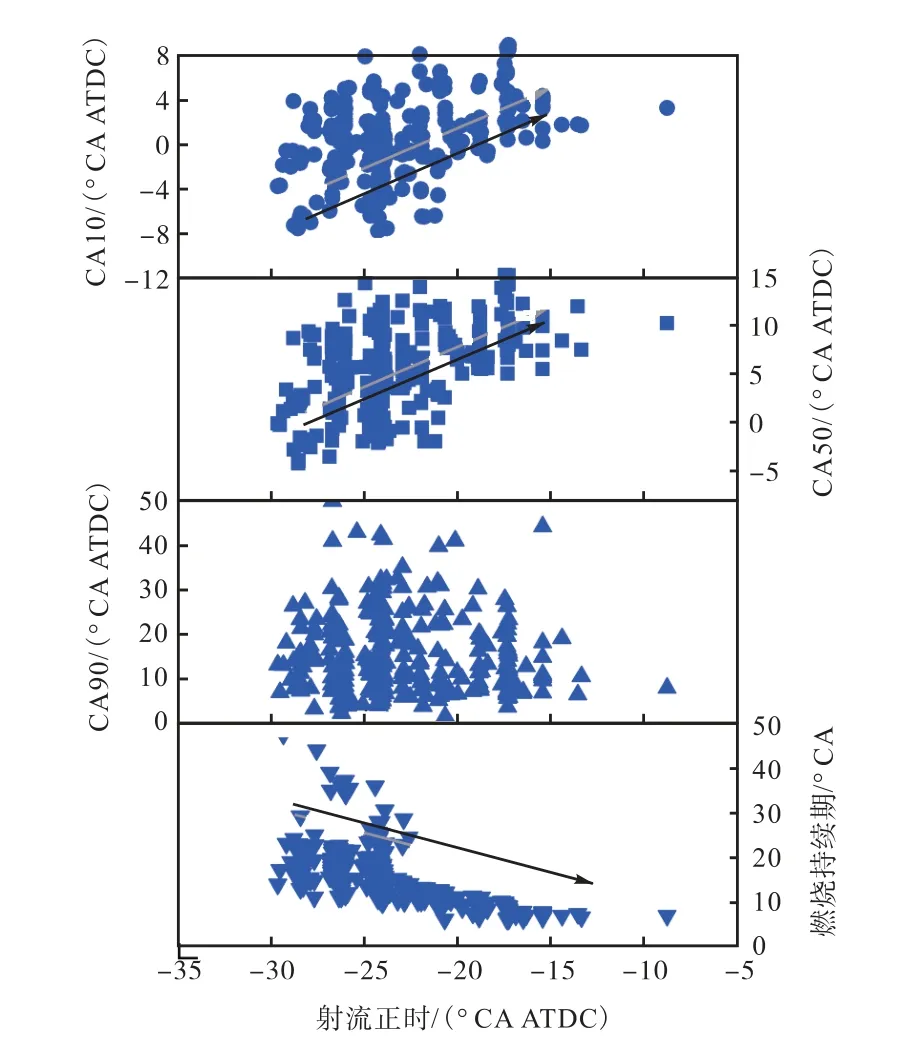
图5 有效解的射流正时对CA 10、CA 50、CA 90 和燃烧持续期的影响Fig.5 The effects of SOIjet on CA 10，CA 50，CA 90 and combustion duration for effective solutions

图6 所示为预喷正时与燃烧过程中CA 50-CA 10 和CA 90-CA 50 的关系，由图可知随预喷正时的变化，CA 50-CA 10 变化较小，这是由于柴油射流正时对于着火相位CA 10 和燃烧相位CA 50 起较强的控制作用.而CA 90-CA 50 则随预喷正时的变化有着明显的下降趋势，说明燃烧过程后期的燃烧速率加快，燃烧结束时刻提前.以上结果说明，预喷正时对于燃烧前期影响很小，而对于燃烧后期有着较大影响.

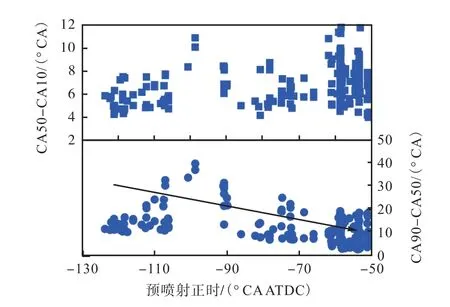
图6 有效解的预喷正时对燃烧过程CA 50-CA 10 和CA 90-CA 50的影响Fig.6 The effects of SOIpre on CA 50-CA 10 and CA 90-CA 50 for effective solutions

2.2 设计算例的演变过程

在图4 所示的有效解的基础上，根据国Ⅵ排放法规，对算例进行进一步的筛选，过滤掉不满足国Ⅵ排放标准的算例，剩余的算例则构成最终的优化解集合，用于后文的研究讨论，在经过国Ⅵ排放标准的二次筛选之后，有效解的大部分结果可以排除，剩余的部分称为第一优化解.

图7 所示为第一优化解的REISFC与THC＋CO的关系，该集合的REISFC主要与THC＋CO 的总体排放量成正相关，且表现为线性关系，这是由于柴油机运行过程中燃料的损失与热效率的降低主要来自未反应燃料THC 和燃料没有充分燃烧产生的CO，因此对THC＋CO 的约束可以近似转化为对燃油消耗率的限制.将REISFC小于210 g/(kW·h)的算例定义为经济性较好的算例，即第二优化解，并在图中用实心图标标识.得到的结果如图8 至图11 所示.

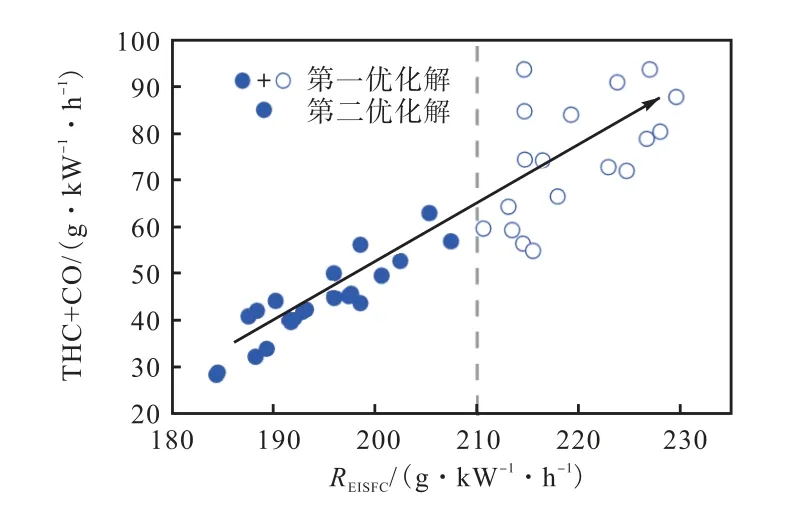
图7 第一优化解的REISFC 与THC＋CO的关系Fig.7 The relationship between REISFC and THC ＋CO for the first optimized solutions

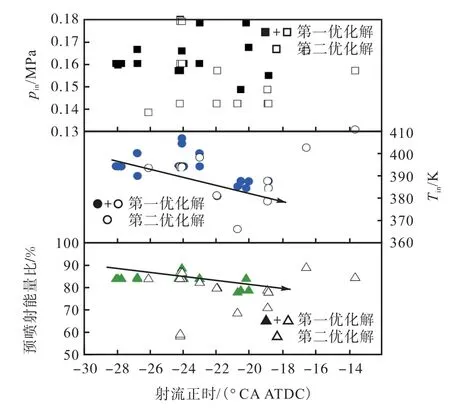
图8 第一优化解的初始参数分布情况Fig.8 The distribution of initial parameters for the first optimized solutions

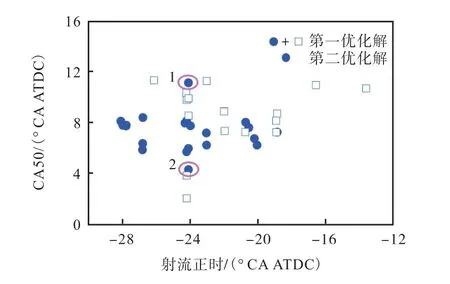
图10 第一优化解的CA 50与射流正时的关系Fig.10 The relationship between CA 50 and SOIjet for the first optimized solutions

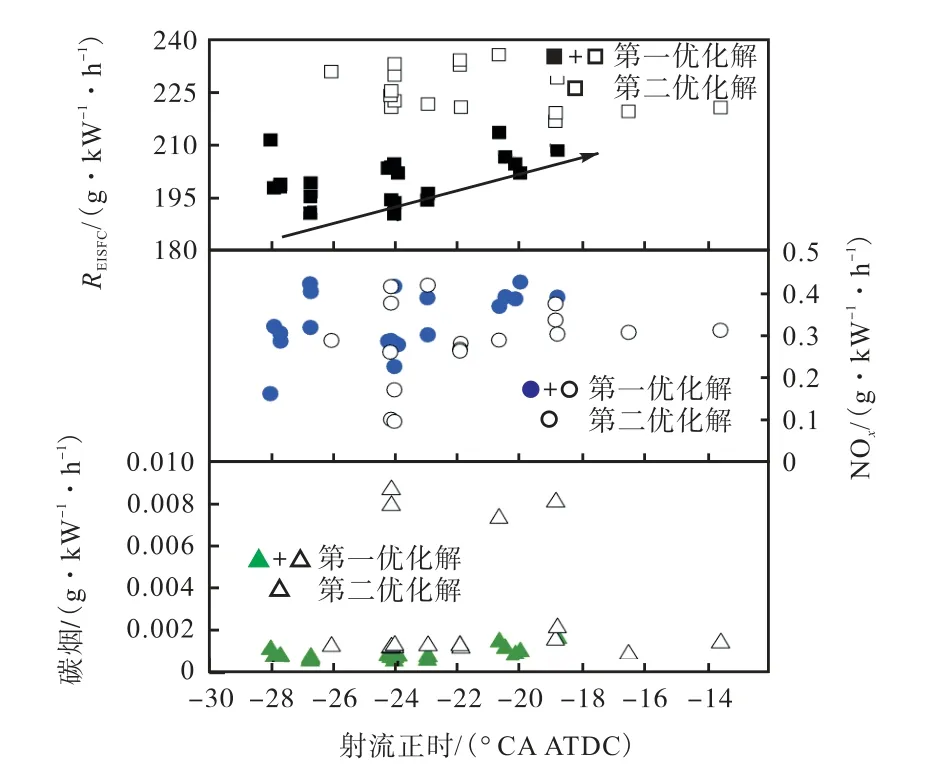
图11 第一优化解的射流正时与REISFC、NOx、碳烟的关系Fig.11 The relationship between REISFC，NOx，碳烟and SOIjet for the first optimized solutions

图8 所示为第一优化解的初始参数分布情况，可以看出在整个射流正时区间内，只有当射流正时早于18.9°CA ATDC 时，才能实现较高的燃油经济性，即图中开始出现第二优化解.这主要是因为一方面，射流正时过晚导致较为滞后的燃烧相位，活塞下行速度加快，因此燃烧过程的做功能力下降；另一方面，当射流正时过晚，充足的时间导致部分预混合气在缸内扩散至活塞与缸壁间的细小缝隙中，无法参与缸内燃烧过程，未燃燃油会随着废气排出发动机，从而导致燃油损失以及排放物中THC 的增加.

随着射流正时的推迟，初始压力的分布较为分散，即初始压力与射流正时在整体上没有显著关联，说明初始压力对于设计算例中燃油经济性的影响较小.此外，第二优化解的初始温度均在380～405 K之间，随着射流正时的推迟，初始温度整体表现出下降的趋势.图中的预喷射能量比和射流正时的关系与初始温度类似，预喷射能量比在图中分布更为紧凑，最优算例仅出现在预喷射能量比处于77%～88%之间，说明该温度范围和预喷射能量比区间是本文所述模式下的最佳选择.

由图8 可以看出，初始温度与预喷射能量比的整体趋势和分布情况类似，因此，将二者的关系进一步分析，得到如图9 所示的结果.第一优化解的初始温度与预喷射能量比成正比，即随预喷射能量比的增大，初始温度需求相应增加.这是由于汽油的活性低于柴油，当预喷射能量比增大，即燃料中的汽油占比增加时，需要提高初始温度来保证发动机运行在合适的燃烧相位时刻，以避免由于燃烧时刻推迟所导致的经济性损失.当预喷射能量比在84%附近时，第二优化解的初始温度在图中表现较为分散，这是由于这些点对应的初始压力、预喷正时以及射流正时存在差异，同样保证了合适的燃烧相位.

图10 所示为第一优化解的CA 50 与射流正时的关系，可以看出，随着射流正时的改变，CA 50 在图中的分布基本不变，近似处于5～9 °CA ATDC 之间，说明燃烧相位在该区间范围内，可以得到较优秀的发动机性能.图中的1、2 两点位于这一区间之外，且偏离较为严重.这是由于虽然1 点与2 点射流正时几乎一样，但是在包括初始压力、初始温度和预喷射能量比在内的其他初始参数影响下二者在CA 50上有了显著差异.不过，1 点EISFC 虽然有所增加，但是NOx远低于0.4 g/(kW·h)；2 点NOx虽然接近阈值，但是REISFC较为优秀，所以二者依旧属于第二优化解集合.过高的现象，进而导致缸内局部温度较高，因此NOx就无法达到更低的水平.

图12 所示为第一优化解的射流正时与预喷正时的关系，可以看出，射流正时与预喷正时的关系较为复杂，根据两个参数的数值分布情况，可以将所有的有效解分为多种类型.其中当射流正时与预喷正时分别为早早、早晚和晚晚时均存在较为优秀的有效解，仅在射流正时较晚而预喷正时较早时不存在有效解，这是因为相比较于前三者，此时射流与预喷射之间的间隔较长，燃料在缸内过于稀薄，大大降低了过程的热效率，导致此时的REISFC无法满足有效解要求.同时，根据上文分析及前期试验结论，射流正时以及预喷正时对JCCI 模式性能的影响最为显著，为了进行更进一步的对比研究，分别选择射流正时与预喷正时均为早期和均为晚期的两个算例作为典型算例，即图中所示的算例A、算例B 两点.

图12 第一优化解的射流正时与预喷正时的关系Fig.12 The relationship between SOIpre and SOIjet for the first optimized solutions

2.3 典型算例对比

根据上文分析选择图12 中的两个典型算例即算例A 和算例B，二者均可以满足国Ⅵ标准，并且具有较高的燃油经济性.为了研究两个典型算例的具体差别，本小节将对二者进行分析.两个算例的运行参数如表4 所示.

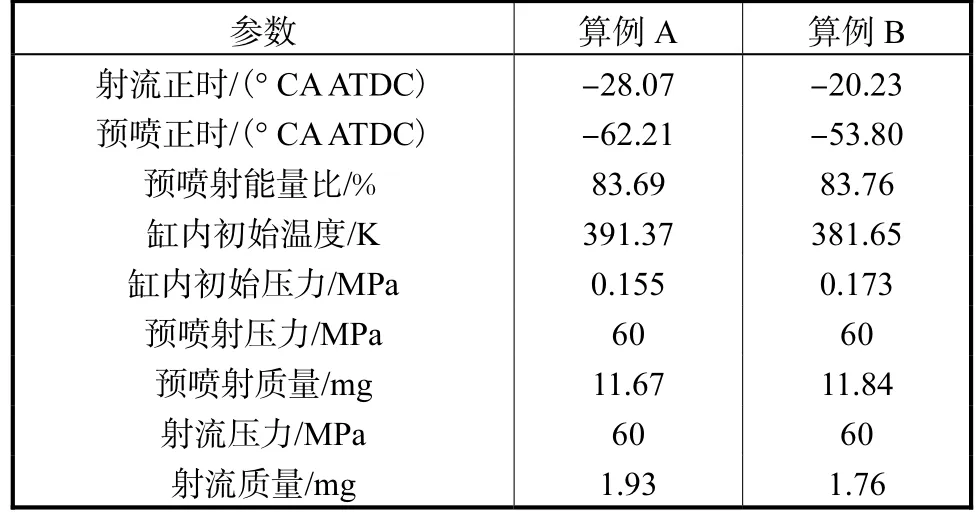
表4 典型算例的参数Tab.4 The operating parameters of typical cases

为了更加直观地展示两算例的运行参数和性能参数的区别，采用雷达图的方法进行分析.图13 展示的分别是两个典型算例的运行参数和性能参数目标值在雷达图中的分布.图中，每一个多边形都代表着一个典型算例.可以看出两个算例的燃烧相位接近，但是REISFC和NOx排放存在明显的“trade-off”关系.射流正时与预喷正时均较为提前的算例A 的NOx排放较低，但燃油经济性较差.因此，为了进一步分析两个算例在REISFC上所表现出的差异的原因，对算例A 与算例B 的气缸压力和放热率进行对比.

图13 两典型算例对比Fig.13 The comparison of two typical cases

图14 所示为两个算例的缸内压力与放热率曲线，由于算例B 的初始压力较高、初始温度较低，因此算例B 的初始缸内介质密度较大，并且具有更高的压缩终点压力和温度.且B 的射流正时较晚，局部较浓的高活性燃料在高温高压条件下更易发生自燃，因此导致即使算例B 的射流正时较晚，但是着火时刻CA 10 早于算例A.同时可以看出，预喷正时和射流正时均较早的算例A 具备单阶段高温放热特性，接近于较为均质的PCCI 模式，而预喷正时和射流正时均较晚的算例B 呈现两阶段高温放热特性，且初始放热速率和最高放热速率均高于算例A，即算例B的燃烧速度更快，其燃烧持续期相对算例A 缩短了3.96 °CA，做功能力增强，因此算例B 的REISFC比算例A 降低了6.80 g/(kW·h).

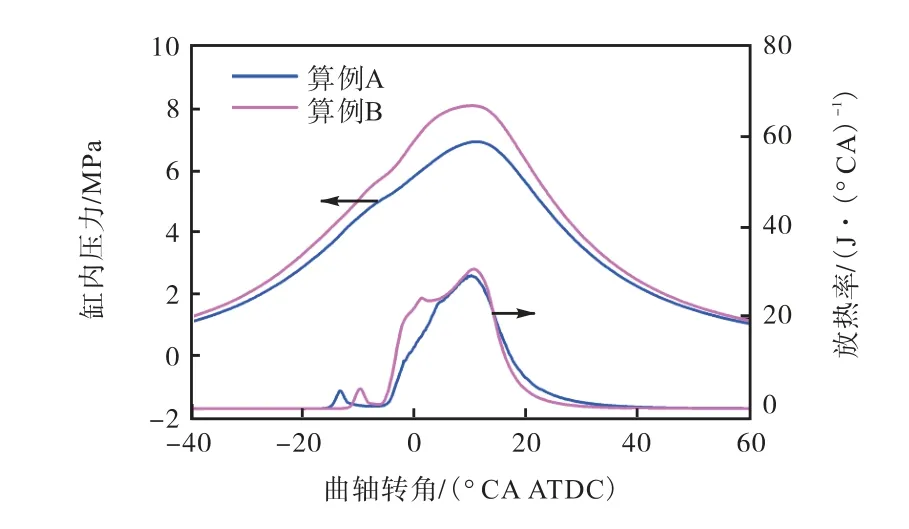
图14 两个典型算例的缸压与放热率曲线Fig.14 In-cylinder pressure and heat release rate of two typical cases

图15 为两个算例不同曲轴转角下的缸内温度分布，灰色部分为射流柴油喷雾.由于两个算例各自的喷射时刻不同，因此采用射流喷射后角度进行计时.可以看出，算例B 中的局部高温区域明显大于算例A，这主要是因为，一方面，算例B 的压缩终点温度和压力较高，导致其着火延迟缩短；另一方面，算例B 的预喷正时和射流正时相对较晚，因此算例B的气相燃油与空气的混合时间明显缩短，导致缸内存在局部浓区，浓区内的燃烧产生大面积高温区域，最终导致算例 B 的 NOx排放相较于算例A 增加0.22 g/(kW·h).

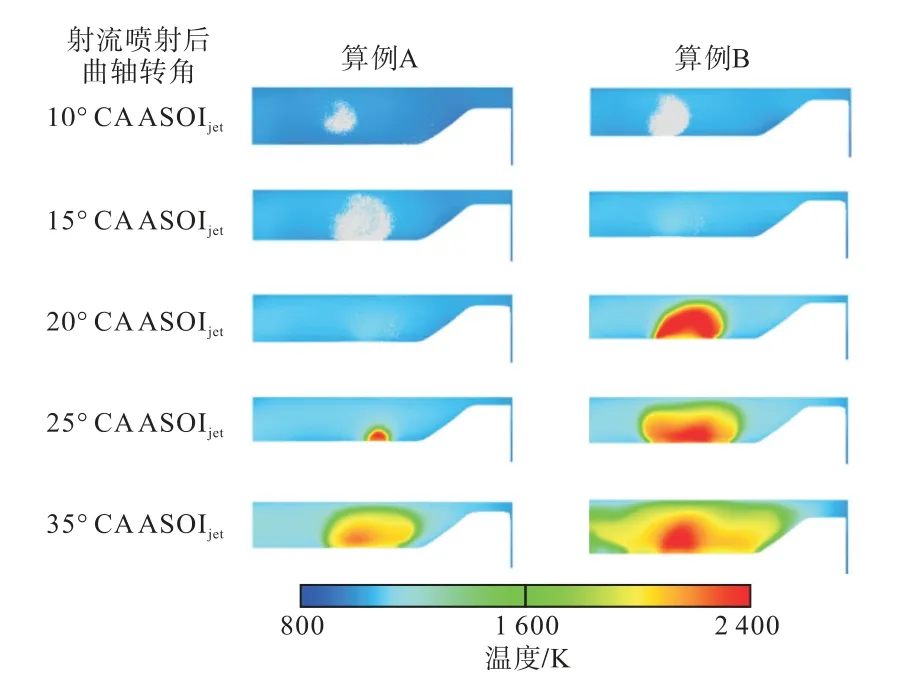
图15 两个典型算例不同曲轴转角下的缸内温度及喷雾分布Fig.15 The in-cylinder temperature and jet-injection diesel spray particles distribution of two typical cases under different crank angles

3 结论

本文以双直喷型柴油JCCI 模式为研究对象，利用三维数值模拟结合遗传优化算法，研究了预喷正时、射流正时、初始温度、初始压力和预喷射能量比等多种初始参数对发动机燃烧和排放性能的影响，得出以下结论：

(1) 双直喷柴油 JCCI 模式中，射流正时对CA 10 和CA 50 起到有效的控制作用，预喷正时的推迟可以明显缩短CA 90-CA 50.

(2) 燃烧相位CA 50 位于5～9°CA ATDC、预喷射能量比在77%～88%之间可以实现较高的发动机性能，且增加预喷射能量比的同时需提高初始温度.

(3) 预喷正时和射流正时均较早(算例A)时，燃烧呈现单阶段高温放热过程；相比于算例A，预喷正时和射流正时均较晚(算例B)时，燃烧呈现两阶段高温放热过程，整体燃耗速率加快，因此REISFC降低6.80 g/(kW·h)，但是局部浓区燃烧产生的高温区域导致NOx排放升高0.22 g/(kW·h).