重塑软土力学特性试验研究

温国胜

（广东省有色金属地质局九四〇队）

0 引言

软土具有典型的蠕变和流变特性，且高含水量、高灵敏性、高压缩性、低抗剪强度的工程力学特性使得其应力应变关系十分复杂，在工程应用中往往遇到不均匀沉降、大位移、大回淤等不良现象，给工程治理带来极大地难度[1]。为了更好地认识软土的力学特性，本文尝试结合实际工程，采用室内试验的方法，进行不同超固结比和应力作用下的三轴试验，进而认识其应力应变演变规律，并构建相关的本构关系模型[2-3]。

1 软土的基本特性

广东省某旅游度假区海景路护岸工程建设护岸长度1945.85m，其中直立式护岸324.49m，斜坡式护岸1621.36m。经现场调查表明，场区主要有5 大层，其工程地质特性分别如下：

①粉质黏土，流～软塑，局部相变为粉土，k7、k10、k11、k13～k16 钻孔（位于养虾池内）表层有厚度为0.2～0.7m 的淤泥，本层土物理力学性质较差，在钻孔揭露范围内分布连续，标贯击数0～3 击，平均标贯击数N＝1.7击，层厚0.20～2.60m。

②1-1层淤泥质黏土（Q42m），流～软塑。本层土物理力学性质较差，在k13～k19 号钻孔区域缺失，平均标贯击数N=2.6 击。层顶深度1.00～2.20m，层顶标高-0.97～0.39m。层厚2.00～8.90m。

②1-2层淤泥质黏土（Q42m），流塑。本层土物理力学性质差，仅在k13～k19 号钻孔区域揭露，平均标贯击数N＝2.3 击。层顶深度0.20～2.60m，层顶标高-1.15～0.42m，层厚2.90～13.40m。

②2层黏土（Q42m），灰色，软塑，本层土呈与粉质黏土互层状，在k4～k7号钻孔区域有厚度为1.2～5.3m的粉砂。本层土在k16～k19 号钻孔区域缺失，平均标贯击数N＝7.3 击，物理力学性质一般。层顶深度3.50～10.60m，层 顶 标 高-9.16～-2.05m。 层 厚1.00～10.40m。

②3层粉质黏土（Q42m），软塑，本层土在k6、k14～k18号钻孔区域呈粉土、粉质黏土互层状。本层土在钻孔揭露范围内分布连续平均标贯击数N=4.9 击，物理力学性质较差。层顶深度5.70～14.80m，层顶标高-13.05～-4.25m，层厚1.00～10.20m。其中k3、k5、k10～k12 钻孔区域层厚1.00～2.90m，其他区域层厚4.00～10.20m。

③粉土，浅灰色，湿，稍密，含云母，局部相变为粉质黏土。本层土在k13～k19 号钻孔区域缺失，平均标贯击数N＝6.6击，物理力学性质一般。层顶深度13.70～16.40m，层 顶 标 高-15.00～-12.25m。 层 厚1.00～2.90m。

该层主要以粉土、粉质黏土为主。自上而下为④1粉土、④2粉质黏土。层顶深度15.70～19.00m，层顶标高-18.13～-14.25m。层厚6.50～9.80m。

④1层粉土（Q41al），中密～密实，本层土在k2、k3、k1l，k14～k16、k18 号钻孔区域相变为粉秒，在k5、k17号钻孔区域夹大量粉质黏土薄层。本层土在k19 号钻孔区域缺失，标贯击数13～33 击，平均标贯击数N＝22.8 击。层顶深度15.70-19.00m，层顶标高-18.13～-14.25m。层厚1.00～5.30m，其中k15～k18 钻孔区域层厚1.00～2.10m，其他区城层厚2.90～5.30m。

④2层粉质黏土（Q41al），可塑，局部相变为黏土。本层土在钻孔揭露范围内分布连续，标贯击数6～13 击。层顶深度18.40～22.40m，层顶标高-21.16～-20.87m，层厚3.90～7.30m。

⑤1层粉质黏土（Q3dmc），软～可塑。本层土在钻孔揭露范围内分布连续，标贯击数5～12 击，物理力学性质一般。层顶深度25.00～27.50m，层顶标高-26.08～-23.63m。本次钻探深度有限，未能穿透该层，揭露厚度2.50～10.90m。

各层土的的力学指标参数如表1所示。

2 重塑软土的应力应变关系试验研究

为了研究重塑软土的应力应变关系，对场区内的软土进行取样，运输至试验室内后进行烘干、研磨筛分、制备泥浆、脱气、堆载预压等程序，制作标准的三轴试验，试验高度为76mm、直径为38mm[4]。试验仪器选用英国GDS 公司生产的GDS 应力路径三轴仪试验系统，具备应力控制、孔隙水压力和控制和银边控制功能。为了更好地对比重塑软土在不同的应力路径下的力学特性、应力应变变化关系，室内试验设置不同的平均固结压力和超固结比工况，在等压固结条件下三轴正常固结不排水剪切试验中，选取的平均固结压力工况分为4 种，分别是工况1：50kPa、工况2：100kPa、工况3：200kPa、工况4：400kPa；在等压固结条件下三轴超固结不排水剪切试验中，选取的超固结比工况也分为4种，分别为工况5：OCR=2、工况6：OCR=4、工况7：OCR=6、工况8：OCR=8，工况5和工况8实验室的平均固结为100kPa。

图1和表2为不同平均固结压力工况下重塑软土的三轴试验应力应变曲线关系。从图1 中可以看出，正常固结重塑软土在不同平均固结压力工况下，重塑软土剪切应力随着轴向应变的变化关系一致，均呈现较为明显的双曲线变化关系，在三轴试验加载初期，剪切应力随着应变的增加而增加，随后增加速率放缓，而在轴向应变达到18%后，剪切应力趋于稳定收敛，随着平均固结压力的增加，剪切应力区域稳定收敛值也不断增加。由此表明，平均固结压力的增加可以使得土体的抗剪切强度得到明显提升。

图1 不同平均固结压力下重塑软土的应力应变关系

表2 不同平均固结压力和超固结比下重塑软土的应力应变测试结果

图2和表2为不同超固结比工况下重塑软土的三轴试验应力应变曲线关系。从图2 中可以看出，不同超固结比工况下，重塑软土剪切应力随着重塑软土剪切应力随着轴线应变的变化关系一致，均呈现较为明显的双曲线变化关系，在三轴试验加载初期，剪切应力随着应变的增加而增加，随后剪切应力增加速率有所放缓，并在达到剪切应力峰值后有略微的降低（超固结比OCR=6 和超固结比OCR=8 时更为明显），达到剪切应力峰值对应的轴向应变随着超固结比的增加而增加。由此表明，超固结比的增加可以使得土体的抗剪强度得到明显提升，并且改善了土体抗剪强度峰值对应的轴向应变值，OCR越大重塑软土的应变软化现象越明显。

图2 不同超固结比下重塑软土的应力应变关系

对不同平均固结压力σ0和超固结比OCR下重塑软土的峰值剪切强度qf进行取值，分别建立qf与σ0、OCR之间的回归关系，得到结果如图3 所示。从图3 中可以看出，随着重塑软土的峰值剪切强度qf与平均固结压力σ0和超固结比OCR之间均具有显著的线性回归关系，其确定系数分别为0.9899 和0.9947，对应的回归关系如公式⑴和公式⑵所示。

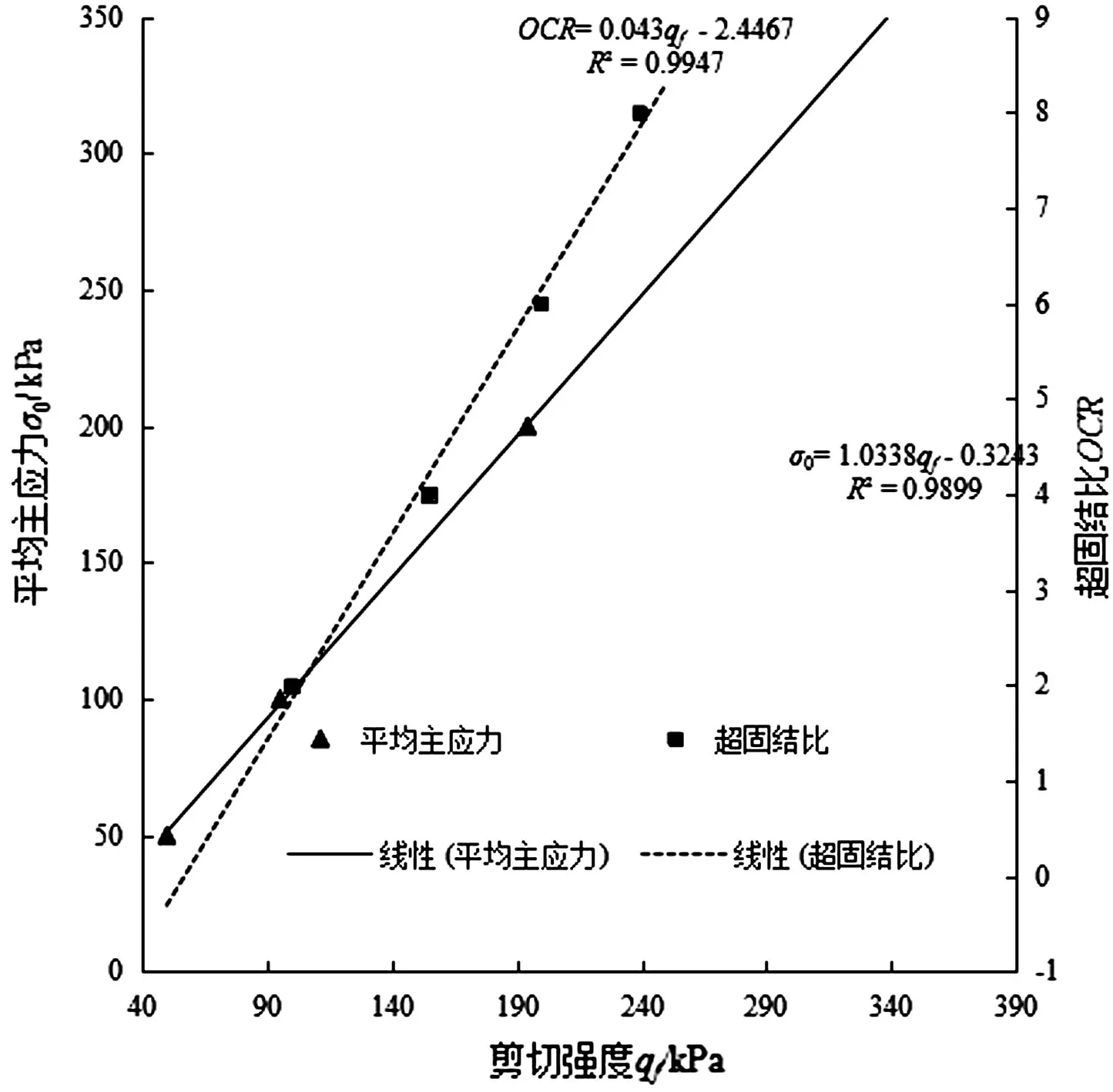
图3 平均固结压力σ0和超固结比OCR与重塑软土的峰值剪切强度qf的拟合关系曲线

3 重塑软土的邓肯-张模型参数

在现有工程设计中，针对软土的本构关系模型有Mohr-Coulomb 模型、Drucker-Prager 模型和邓肯-张模型，其中邓肯-张模型由于能够较好地反应软黏土的力学特性，且参数计算简单，仅有2 个待定常数，可操作性强，因此在工程实践中应用较为广泛。邓肯-张模型认为土体的应力应变关系为典型的双曲线，可以用公式⑶进行计算[5]。

式中，σ1为重塑软土剪切破坏时的主应力，MPa；σ3为重塑软土三轴试验围压，MPa；ε为重塑轴向应变，%；a和b为本构模型待定参数。

通过公式⑶进行求导，可以得到重塑软土的切线模量和泊松比如公式⑷、公式⑸所示[6-8]。

式中，Rf为重塑黏土的破坏比；c为重塑黏土的黏聚力，kPa；φ为重塑黏土的内摩擦角，°；K、n为无因次基数和无因次指数，是决定于土质的试验常数；pa为大气压强，kPa；G、F、A为材料常数。

通过图1 的参数坐标变换，得到ε1/(σ1-σ3)与轴向应变ε1的结果如图4 所示。从图4 中可以看出，在各级围压下，ε1/(σ1-σ3)与轴向应变ε1均呈现明显的线性变化。围压50kPa 时，拟合关系确定系数为0.9741，拟合关系如公式⑹所示；围压100kPa 时，拟合关系确定系数为0.9474，拟合关系如公式⑺所示；围压200kPa时，拟合关系确定系数为0.9835，拟合关系如公式⑻所示；围压400kPa 时，拟合关系确定系数为0.9573，拟合关系如公式⑼所示。

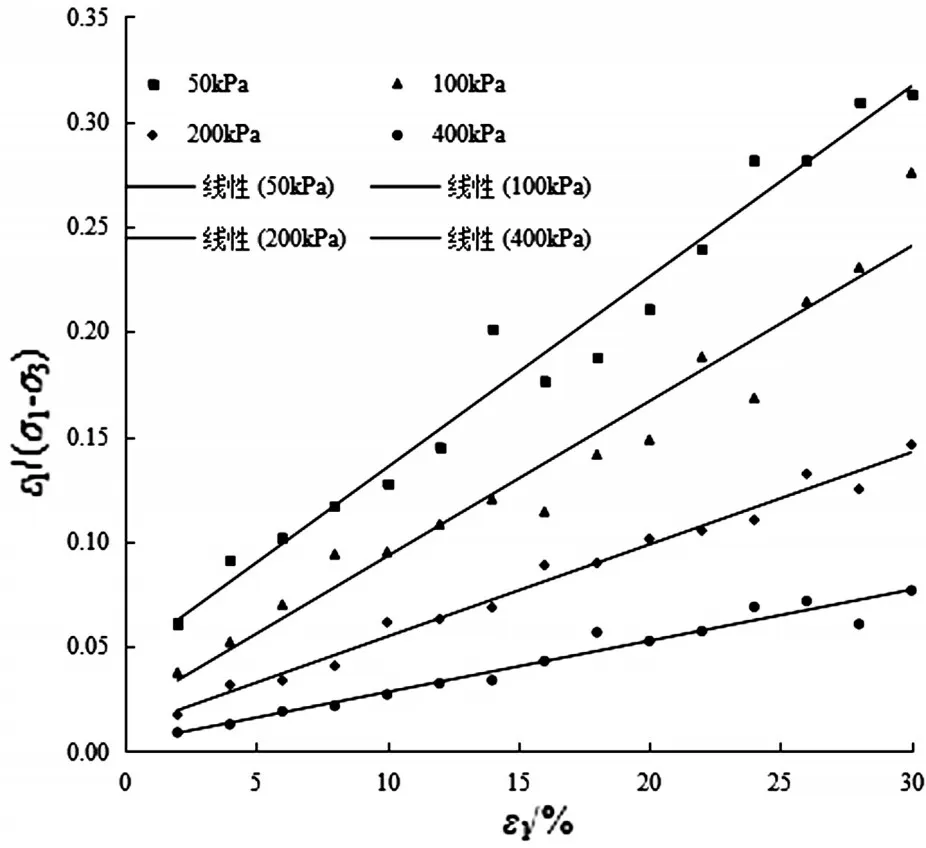
图4 ε1/(σ1 - σ3)与轴向应变ε1的相关关系

由公式⑹～公式⑼，可以计算得到各等级围压下，公式⑶中待定参数，如表3所示。

表3 不同围压下重塑软土的邓肯张模型待定参数确定

4 结论

以广东省某旅游度假区海景路护岸工程为研究对象，运用室内试验的方法，对重塑软土进行三轴固结不排水剪切试验，并求得其邓肯-张本构模型参数，得到以下几个结论：

⑴正常固结重塑软土在不同平均固结压力工况下，剪切应力均随着轴向应变呈现较为明显的双曲线变化关系，随着平均固结压力增加，峰值剪切应力不断增加，平均固结压力的增加可以使得土体的抗剪切强度得到明显提升。

⑵重塑软土在不同超固结比工况下，剪切应力均随着轴向应变呈现较为明显的双曲线变化关系，随着超固结比增加，峰值剪切应力不断增加，超固结比的增加可以使得土体的抗剪强度得到明显提升，OCR越大重塑软土的应变软化现象越明显。

⑶在各级围压下，ε1/(σ1-σ3)与轴向应变ε1均呈现明显的线性变化，确定系数均大于0.9，并确定了重塑软土的邓肯张本构模型待定参数。