弱膨胀土三轴膨胀模型及其应用

李从安,许晓彤,沈登乐,王 卫,胡 波

(1.长江科学院 水利部岩土力学与工程重点实验室,武汉 430010; 2.安徽省引江济淮集团有限公司,合肥 230000)

0 引 言

膨胀性岩土吸湿膨胀易造成边坡失稳,影响工程运行期安全。引江济淮工程是国家重大水利工程之一,其流域内膨胀土(岩)的渠道累计长约119.75 km,边坡加固处理不当不仅威胁工程运行期的安全,同时也会造成后期运维成本增加,上覆压重换填水泥改性土成为处理浅层失稳的常用手段。土膨胀性的不同决定了上覆压重厚度的不同[1],因地制宜,细化压重厚度,厘清膨胀变形机理是十分必要的。

厘清膨胀变形机理进而提出合理的防护方案关键前提是分析建立膨胀变形与各影响因素间的内在关系。传统膨胀模型的建立多基于K0(侧限压缩)应力状态,仅考虑一维膨胀变形,通过建立膨胀变形和膨胀力随初始含水率[2-4]、初始干密度[5]和上覆应力[6-7]等的内在联系,进而提出相应的膨胀模型[8-10]探究膨胀土边坡滑动机理[11]。但侧限条件下的膨胀变形表达式对某些工况如边坡、基坑工程,较难反应其真实应力状态;相比较而言,三轴膨胀模型应力状态清晰、精确度高,可更真实地反映土体的膨胀特性。但因其试验操作复杂,控制因素较多且周期长,使得研究相对较少。刘清秉等[12]基于K0及三轴膨胀模型提出两者间转换关系,并采用反演方法分析了平均侧压力系数的变化趋势,丁秀丽等[13]根据吸湿膨胀模型结合室内试验提出了膨胀性岩石的吸湿膨胀分析方法。膨胀变形受土体含水率变化的影响,既有膨胀模型多基于土体充分吸湿下建立的膨胀数学表达式,较少考虑不同含水率增量下土体的膨胀率,本文通过弱膨胀土的三轴膨胀试验建立考虑含水率变化的膨胀变形表达式,探讨膨胀模型的工程应用,分析弱膨胀土渠坡运行期的稳定性及处理措施,以期为膨胀土的优化设计提供理论依据。

1 低河堤段弱膨胀土特性试验

1.1 基本参数

选取某一均质弱膨胀土断面,边坡最大开挖深度为8.7 m,渠坡坡比1∶3,一级马道高6 m,平台宽2 m,运行期最低输水水位为4.1 m,模型断面如图1所示。地层参数如表1所示,强度准则选择Mohr-Coulomb准则。

表1 弱膨胀土强度参数Table 1 Strength parameters of weak expansive soil

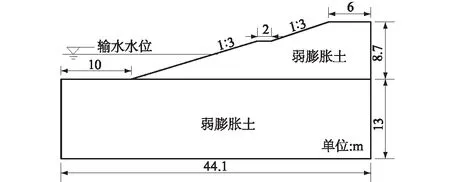
图1 计算断面示意图Fig.1 Schematic diagram of calculated section

1.2 膨胀特性试验

依据《土工试验方法标准》(GB/T 50123—2019),开展弱膨胀土重塑样的无荷、有荷膨胀率试验。不同初始含水率、荷载下的膨胀率试验成果如图2所示。从图2中可以看出,随着初始含水率增大,有荷膨胀率减小;膨胀土的有荷膨胀率随上覆压力增大而减小,同时在较小的上覆压力范围内,膨胀率随荷载增大而急剧降低,说明较小的上覆荷载即可对膨胀土的吸水膨胀产生明显的抑制作用,但随着荷载的继续增大,这种抑制作用则明显减弱。对于天然含水率>20%的弱膨胀土,当上覆压力为6.25 kPa时土体的膨胀变形可忽略不计。

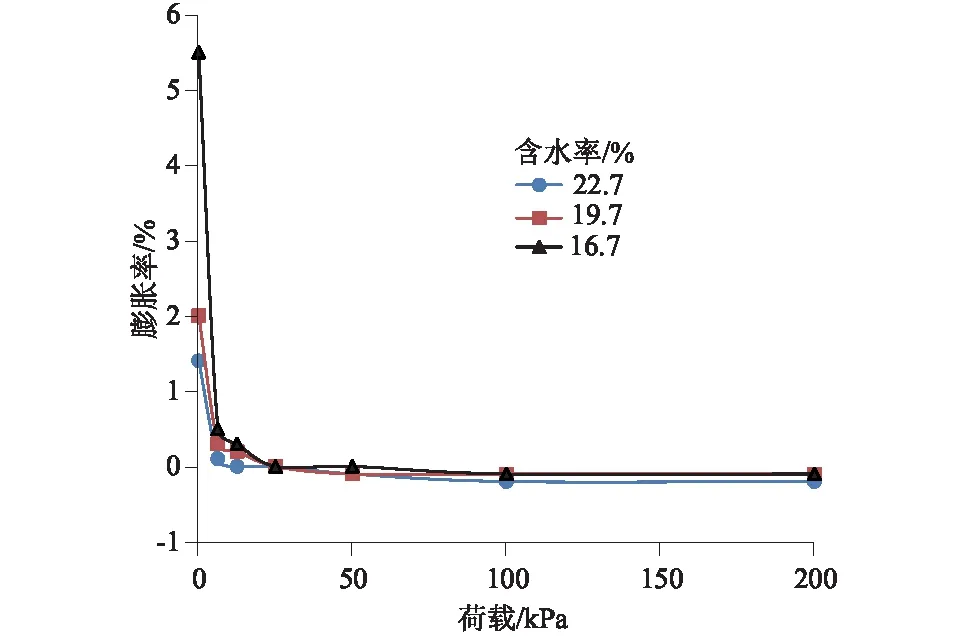
图2 不同含水率下膨胀率随荷载关系的变化曲线Fig.2 Variation curves of expansion rate with load under varied moisture content

1.3 GDS三轴吸湿膨胀试验

膨胀土的三轴吸湿试验在GDS三轴仪上完成,试样选取初始含水率ω0为20.0%,压实度Rc为96%的引江济淮工程弱膨胀土。试验过程同文献[12],整个试验过程中,通过GDSLAB模块软件自动测记压力室内水量变化,得到试样的体积应力(外体变),试验后通过对土样烘干称重,计算其充分吸湿后的终了含水率。通过分析发现体积应变(εv)与平均主应力(σm)近似呈对数变化关系,由于ln(σm)在荷载为0时无数学意义,将σm去单位化,令基准荷载P0=1 kPa,分别建立体积应变(εv)和终了含水率(ωult)随ln(1+σm/P0)的关系如图3。至此,初始含水率ω0为20.0%,压实度Rc为96%的弱膨胀土模型得以建立。

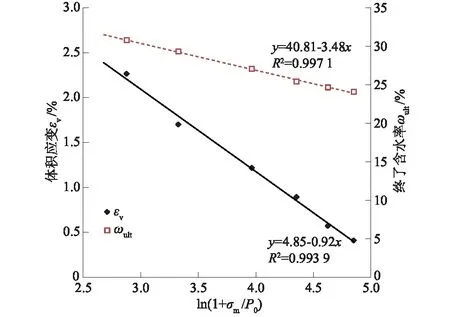
图3 εv和ωult与ln(1+σm/P0)关系曲线Fig.3 Variations of εv and ωult with ln(1+σm/P0)

2 膨胀模型的数值实现与应用

2.1 膨胀模型的数值实现

由图3可见,在三轴应力条件下,体积应变和终了含水率与平均主应力呈现出良好的线性关系,结合文献[14],基于以往大量膨胀土的试验研究[1-2,7],得到如下关系式,即对于某一初始含水率为ω0、压实度Rc的膨胀土,存在体积应变εv、终了含水率ωult与平均主应力ln(1+σm/P0)的数学关系式为:

εv=A-Bln(1+σm/P0) ;

(1)

ωult=C-Dln(1+σm/P0) 。

(2)

式中A、B、C、D均为系数。

在进行膨胀土边坡填筑层变形和稳定性分析的计算中,当考虑含水率由初始含水率ω0增加至某一含水率ωi,含水率增量Δωi引起的体积变形εvi可表示为

对于初始含水率ω0=20.0%,Rc=96%的引江济淮弱膨胀土样,因节点单元应力、含水率变化而引起的体应变可表示为

基于式(4),根据湿度场理论[15]和膨胀应变为各向同性的假定,得到

εvi/3=εx=βΔt。

(5)

式中:εx为节点线性应变;β为膨胀系数,可根据K0膨胀试验反演求得;Δt为湿度变化量。数值计算中通过将εvi换算成等效节点湿度荷载,再施加到计算模型中,即可推求不同含水率增量下边坡的膨胀变形。

2.2 膨胀模型的应用

2.2.1 三轴膨胀模型与K0膨胀模型的关联性

基于Einstein体积膨胀假说:起始条件相同的同一种膨胀土,其体积膨胀应变的单因素表达式不随偏差应力的变化而变化,即体积应力相同时,无论三轴试验还是侧限条件,其膨胀体积应变理论上是不变的,即

δef=δv。

(6)

式中δv为体积膨胀率。

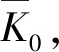
(7)

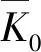
(8)

式中k1、k2为常数,可通过K0与三轴膨胀试验反演计算求得。文献[12]给出某一中膨胀土参数k1=0.128 6,k2=1.365 8。将式(6)、式(8)代入式(3)得到

(9)

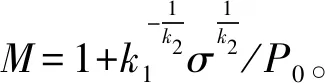
由此将三轴应力状态下膨胀模型转变为K0状态下膨胀模型,得到不同含水率增量下土体的膨胀率,当土体充分吸湿后,其膨胀率可表示为

(10)

2.2.2 膨胀土压重厚度估算

对于一个倾角为α的均质膨胀土渠坡,当采用压重处理渠坡临空面膨胀变形时,假设控制坡面膨胀应变<ε(ε为定值),根据式(9),得到垂直于坡面的上覆荷载为

(11)

设衬砌的重度为γ衬砌,厚度为hx,则垂直于坡面方向荷载分量为γ衬砌hxcosα,代入上式得到衬砌厚度为

(12)

式(12)为土层平均含水率增加Δω时所需衬砌厚度的理论公式,在实际工程中,还需考虑大气影响深度、基质吸力等因素对膨胀性的影响,从而综合分析确定一个合理值。

3 渠坡膨胀变形分析

3.1 初始状态

数值模型主要考虑膨胀土渠坡浅层2 m深度范围内的吸湿变形,地下水位取渠道运行期最低输水水位4.1 m,不考虑渠道水位变动对渠坡的变形影响,研究边坡2 m深度内含水率由初始状态变化到充分吸湿状态的膨胀变形,边坡初始饱和度分布场如图4所示。

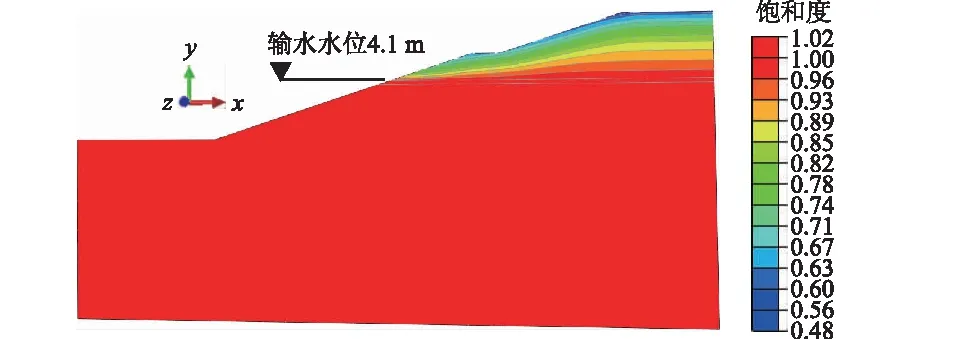
图4 初始状态饱和度分布云图Fig.4 Contours of saturation at initial state

3.2 膨胀变形数值分析

考虑吸湿膨胀的弱膨胀土渠坡应力场分布如图5所示,图中应力符号拉为正,压为负。

图5 顺坡向正应力和剪应力等值线Fig.5 Contours of normal stress and shear stress along the slope

从图5可以看出:

(1)膨胀变形引起渠坡应力发生变化,各应力分量分布形式略有不同,在边坡坡脚及吸湿与非吸湿界面处应力相对集中。

(2)边坡吸湿后吸湿区沿顺坡向膨胀伸展,但受到非吸湿区的约束作用,使得吸湿区顺坡向正应力明显增加,非吸湿区应力减小。

(3)由于吸湿区与非吸湿区间的约束与被约束关系,使得两区之间产生顺坡向的剪应力,两者沿着某一中性点逐步自平衡并在水位交界和二级坡脚薄弱点产生应力集中。

3.3 压重处理效果分析

为了反映不同压重厚度对膨胀变形的抑制效果,分析了无处理层与0.3 m(5.4 kPa)、0.5 m(9.0 kPa)压重下边坡的塑性区分布,如图6所示,无压重处理时充分吸湿下边坡塑性区深度达0.6 m,采用0.3 m压重下,仅坡脚处存在局部塑性区,采用0.5m压重时无塑性区分布。由于该分析成果未考虑上覆压重层对下卧膨胀土层保湿降燥的有利影响,综合分析,可采用0.3 m(5.4 kPa)的压重厚度对该膨胀土进行处理,这与1.2节有荷膨胀试验所述上覆压力基本一致。

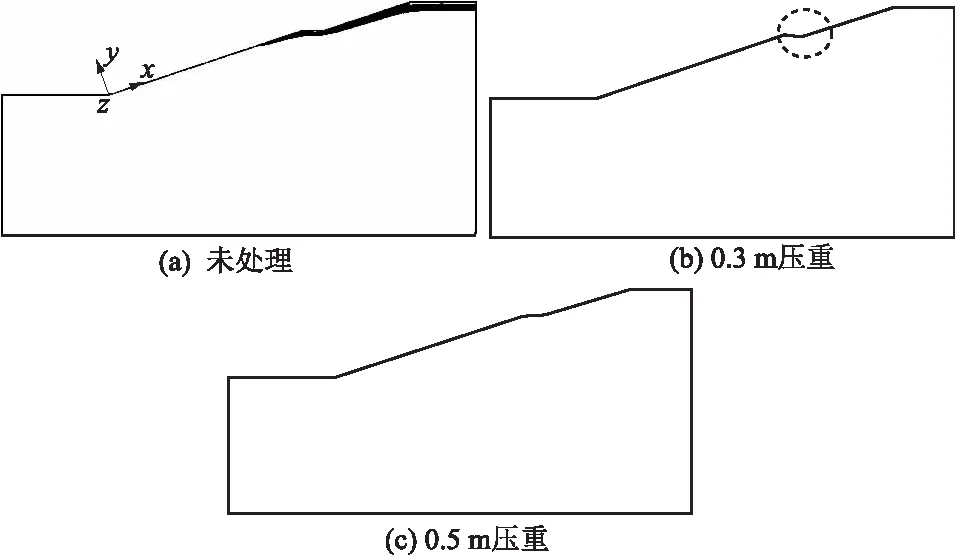
图6 不同压重厚度下等效塑性应变分布Fig.6 Distribution of equivalent plastic strain with different compressive thicknesses

4 结 论

(1)基于三轴吸湿膨胀试验建立了体应变、终了含水率与平均主应力关系的数学表达式,提出了不同含水率增量下的三轴吸湿膨胀模型,以及K0和三轴膨胀模型的转化关系,探讨了膨胀模型的工程应用。

(2)基于已建立的三轴膨胀模型,分析了引江济淮弱膨胀土段渠坡应力分布特征,得到顺坡向剪切应力集中是引起渠坡失稳的关键因素。

(3)分析了不同压重厚度下弱膨胀土的膨胀变形,结果表明,采用5.4～6.25 kPa左右的压重荷载即可抑制渠坡运行期的膨胀变形,研究成果为类似膨胀土渠坡处理提供参考。