基于优化BP神经网络的连续管疲劳寿命预测*

窦益华 张佳强 李国亮 韦 亮 曹银萍

(1.西安石油大学机械工程学院 2.中国石油西部钻探公司试油公司)

0 引 言

与传统作业方式和设备相比，连续管作业具有作业安全、操作方便、节约成本等优点。目前，连续管已广泛应用于测井、完井及修井等作业中。然而，连续管在作业中容易发生变形和失效，主要原因是内压与反复的塑性弯曲[1]。缠绕在滚筒上的连续管在1个完整的起下过程中需要经过6次塑性变形，反复的塑性变形将对连续管的疲劳寿命产生不利影响，因此预测连续管的疲劳寿命非常必要。

目前仅有少数学者通过人工神经网络开展连续管研究。李继红等[2]通过BP神经网络预测连续管TIG焊接头薄弱区的力学性能。彭嵩等[3]基于LMBP神经网络预测连续管疲劳寿命。于桂杰等[4]建立了RBF与SOFM混合神经网络的连续管疲劳寿命预测模型。

为了避免标准BP神经网络预测连续管疲劳寿命时容易陷入局部极小值和训练时间过长的问题，本文通过MATLAB编写程序，利用有动量的梯度下降法、拟牛顿算法和一步正割算法分别优化标准BP神经网络[5-8]，选择优化后网络性能最佳的网络模型以预测连续管疲劳寿命，并提出了连续管区间寿命预测方法。所得结果可为连续管的寿命预测提供参考。

1 BP神经网络原理与优化

1.1 BP神经网络模型构建步骤

人工神经网络通过模拟生物神经网络结构对外界输入信息进行处理并得出结果。BP神经网络作为一种多层向前型神经网络，在输入向前传播的同时也能使输出误差不断向后反向传播以提高预测精度，是目前应用非常广泛的神经网络模型[9-11]。BP神经网络主要由输入层、隐含层和输出层构成。图1为BP神经网络结构示意图。其中X、Xi和Xn代表学习样本，Q1、Qi和Qm代表预测目标，W、i和j代表神经网络的阈值与权值。

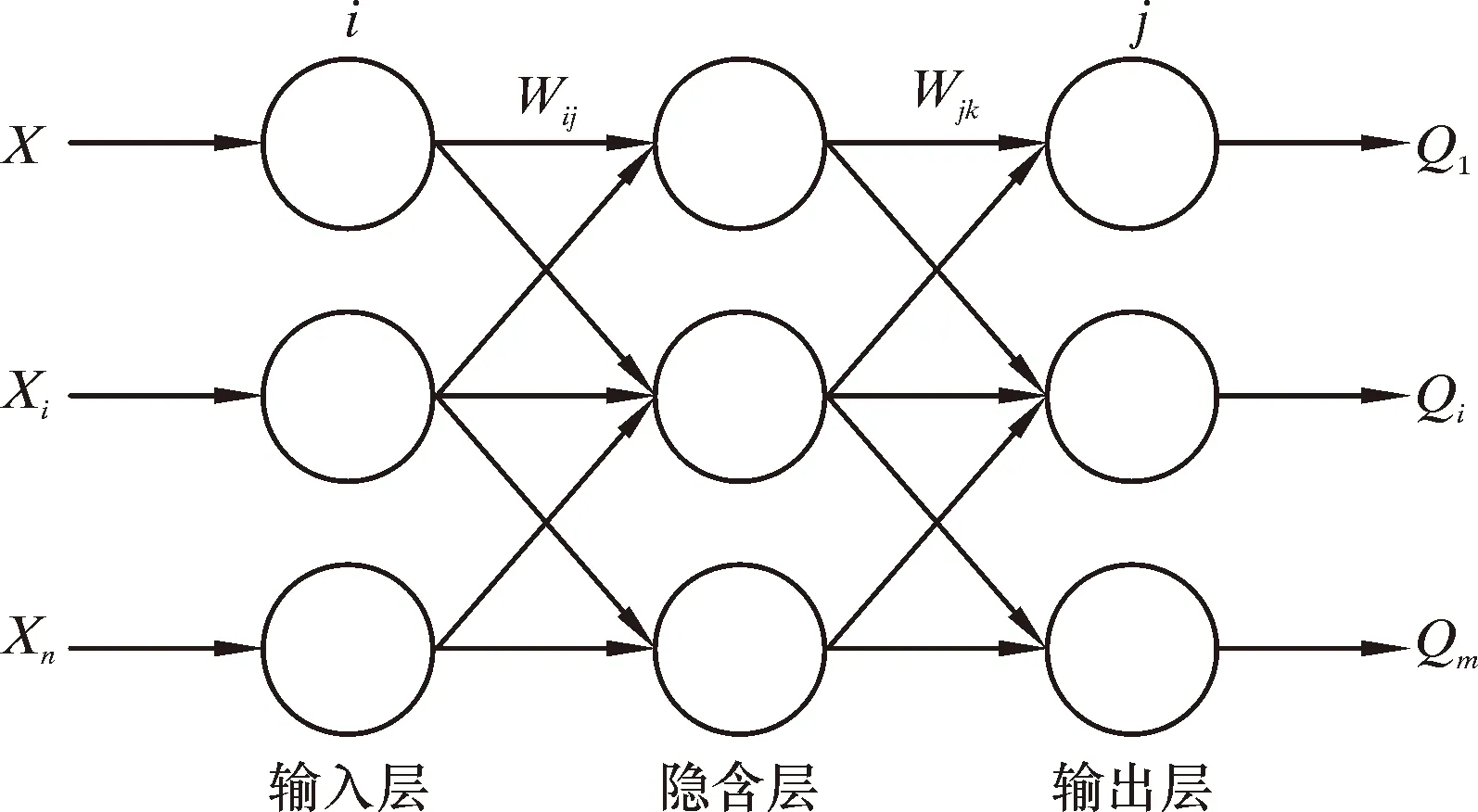
图1 BP神经网络结构示意图Fig.1 Schematic structure of BP neural network

BP神经网络构建步骤如下。

(1)数据集划分。将疲劳试验装置获得的连续管疲劳寿命数据作为样本合集，划分样本训练集与测试集。

(2)训练样本归一化。连续管疲劳寿命的各项参数指标之间存在较大差异，为加快网络学习速率需要对数据进行归一化处理，通过MATLAB中的Mapminmax函数将数据集归一化，依据激活函数值域，将其归一化至[-1，1]之间。

(3)构建BP神经网络。确定网络层数与各层节点数[12-14]，初始化各层权值与阈值。构建3层BP神经网络，其中输入层节点数为4，分别代表连续管外径、壁厚、弯曲半径以及内压。

(4)网络参数配置。确定网络学习训练次数、学习速率以及训练目标最小误差。

(5)计算网络各层输出向量与网络误差。网络第k层神经元j具有下式输入输出关系[3]：

NPj=∑(WjiQPi-bj)

(1)

Qpi=fj(NPj)

(2)

式中：P为输入样本；Wji为k-1层的第i个神经元到神经元j的连接权值；bj为初始的阈值；fj为传递函数，采用purelin函数，选取梯度下降法训练。

(3)

式中：x为连续管因素归一化后的列向量与阈值整合后的结果。

(6)样本实际输出与期望值误差Ei计算。Ei计算式为：

(4)

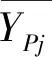
(7)误差反向传递与权值、阈值修正。对比期望值与网络实际输出值误差，BP神经网络通过损失函数LOSS将误差反向传播到网络中，对各层连接权值与阈值进行调整。权值与阈值更新公式为：

(5)

(6)

式中：W1和b1分别为更新后权值和阈值；η为学习率，取η=0.01。

(8)循环步骤(7)与步骤(3)进行更新反馈，直至达到训练要求。

1.2 BP神经网络优化

标准BP神经网络容易陷入局部极小值且训练时间过长[15-16]。优化BP神经网络训练方法可避免此类问题。BP神经网络训练优化方法与对应训练函数如下：有动量的梯度下降法(Traingdm)、自适应lr梯度下降法(Traingda)、弹性梯度下降法(Trainrp)、拟牛顿算法(Trainbfg)、一步正割算法(Trainoss)及Levenberg-Marquardt(Trainlm)法。本文选用有动量的梯度下降法、拟牛顿算法与一步正割算法作为BP神经网络优化方法。

2 优化BP神经网络模型构建

2.1 连续管疲劳寿命预测学习样本选取

通过文献调研，将文献[4]与文献[6]学习样本中部分标准试验机获得的连续管疲劳试验数据进行汇总，汇总后的20组数据如表1所示。将样本编号为3、8、9和15的数据组作为预测样本，其余数据组作为学习样本。

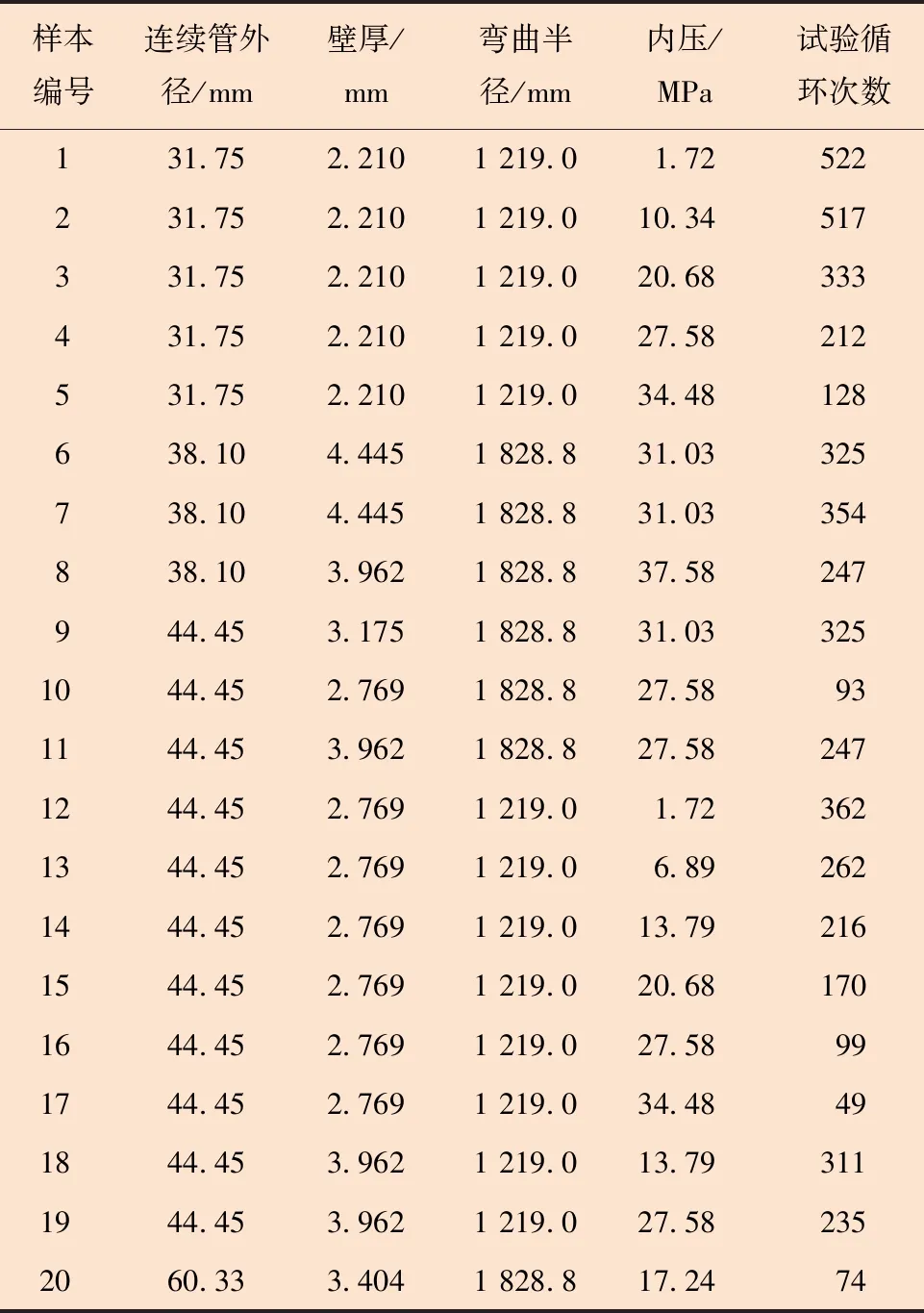
表1 连续管疲劳数据汇总Table 1 Fatigue data collection of coiled tubing

2.2 连续管疲劳寿命预测网络结构确定

连续管外径、壁厚、弯曲半径[17]以及内压是影响其疲劳寿命的主要因素，构建3层BP神经网络，其中输入层节点数为4，分别代表连续管外径、壁厚、弯曲半径以及内压。输出层节点数为1，代表连续管疲劳寿命。隐含层节点数应在保证精度的前提下尽量使网络结构紧凑。先用经验公式确定隐含层的节点数，具体如下：

(7)

式中：n1为隐含层节点数；n为输入层节点数；m为输出层节点数；c为常数，取值范围[1，10]。

在经验确定隐含层节点数的基础上，通过实际训练再次确定。通过实际训练确定隐含层节点数时，先预设一个较小隐含层节点数，依次递增节点数直至满足训练要求，此时对应节点数为隐含层最佳节点数。

本文对BP神经网络结构中隐含层节点数确定时，依据式(7)求得对应节点数理论区间为[3，12]，预设隐含层节点数为3，依次增加节点数开始训练网络，直至满足训练要求。当网络结构中隐含层节点数为4时，BP神经网络在训练第10轮获得最佳验证性能(第4轮均方误差为0.001 352 9)，且测试集预测值与实际值误差较小，满足预测精度要求。训练结果如图2所示。

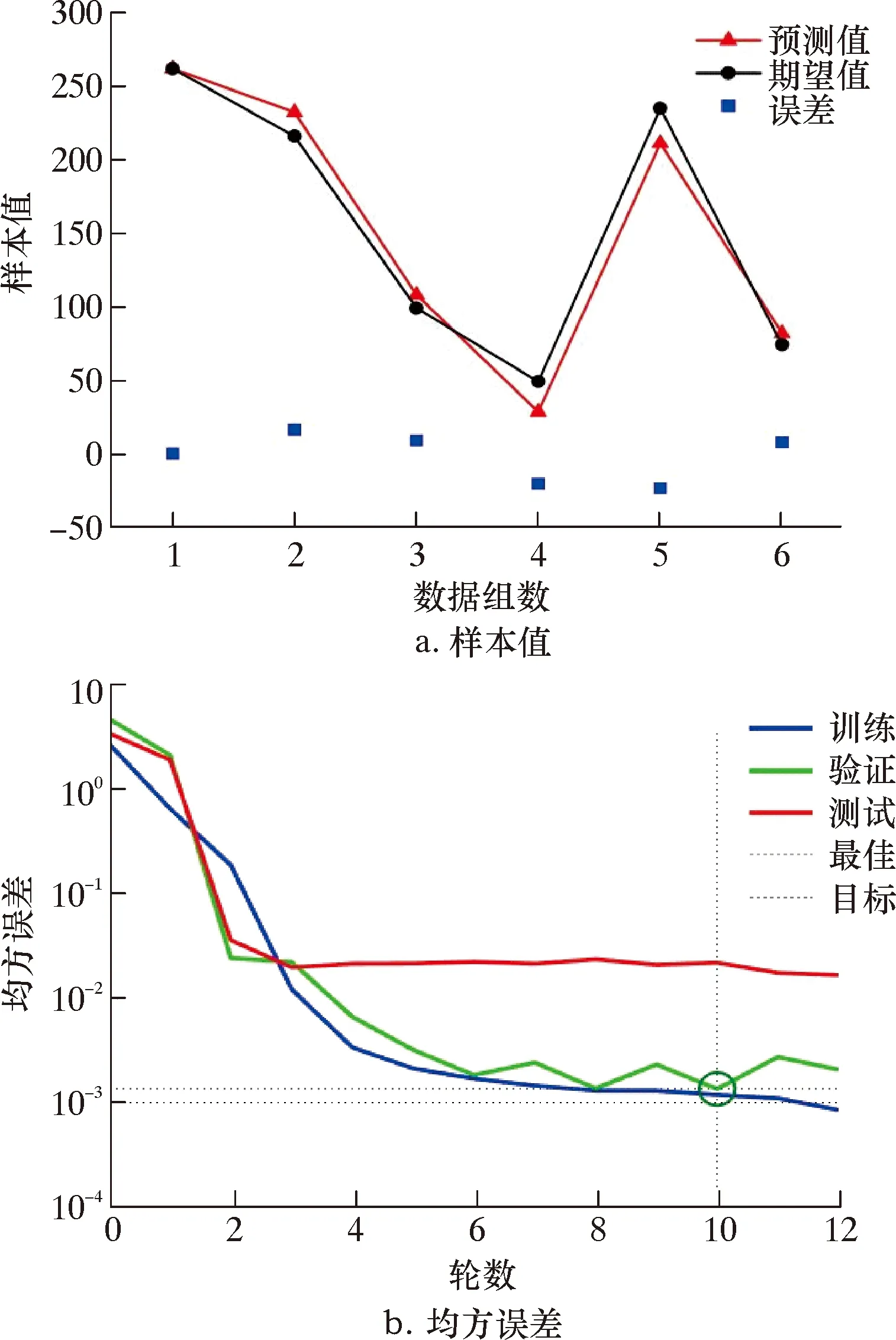
图2 隐含层节点数为4时的网络训练结果Fig.2 Network training results when the number of hidden layer nodes is 4

确定优化后的BP神经网络模型结构为4-4-1。优化后网络参数为：隐含层节点数4，传递函数为Tansig函数与Purelin函数；训练方法为：有动量的梯度下降法、拟牛顿算法与一步正割算法。设置网络最大训练次数为2 000次，学习速率为0.01，训练精度为0.001。

3 连续管疲劳寿命预测

3.1 单层寿命预测

按照BP神经网络参数构建BP神经网络模型，利用有动量的梯度下降法、拟牛顿算法和一步正割算法[18]优化BP神经网络，考虑连续管外径、壁厚、弯曲半径以及内压为连续管疲劳寿命主要影响因素，得到如图3所示的BP神经网络测试集的预测值与实际值对比图。图3中红色线条代表BP神经网络的连续管疲劳寿命预测曲线，黑色线条为试验得到的连续管疲劳寿命曲线，蓝色点对应样本值代表连续管疲劳寿命预测值与试验结果的误差。

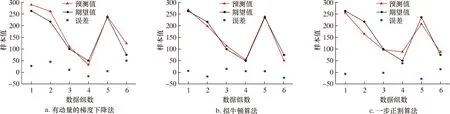
图3 不同优化方法下网络训练结果对比图Fig.3 Comparison of network training results under different optimization methods

对比图3中有动量的梯度下降法、拟牛顿算法和一步正割算法优化后BP神经网络训练结果，计算不同优化方法下BP神经网络测试集的预测值与实际值误差，并计算6组样本数据中的预测平均误差，结果如表2所示。6组样本数据中，利用有动

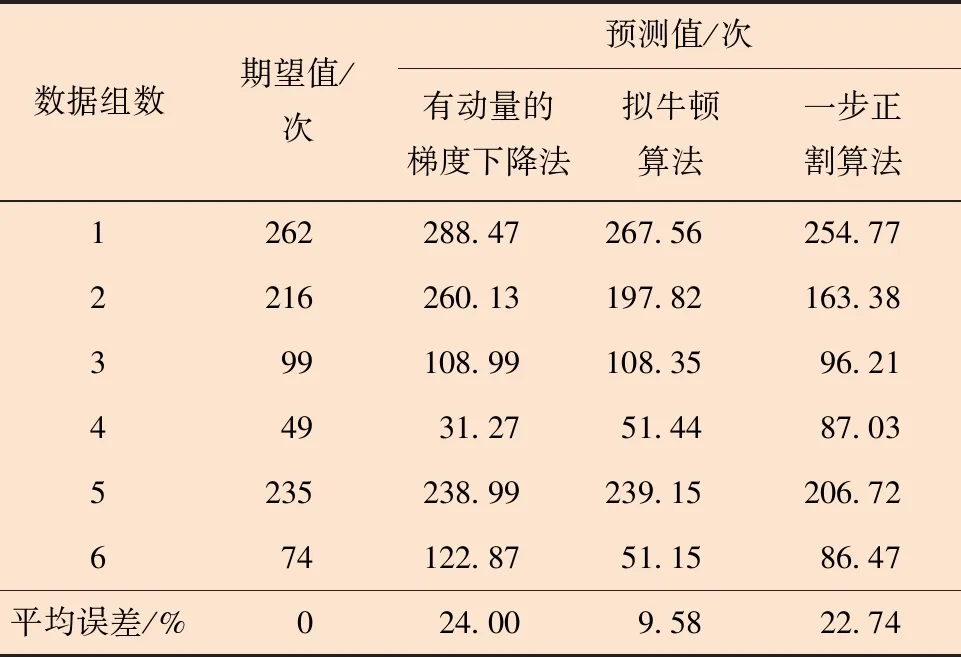
表2 不同优化方法下网络训练结果误差Table 2 Error in network training results under different optimization methods

量的梯度下降法、拟牛顿算法和一步正割算法优化后的BP神经网络预测连续管疲劳寿命平均误差分别为24.00%、9.58%和22.74%。据此，得出3种优化方法的性能为：拟牛顿算法最优，一步正割算法其次，有动量的梯度下降法最差。

分析结果表明，拟牛顿算法优化后的BP神经网络具有最佳性能，确定通过拟牛顿算法优化后的BP神经网络预测连续管疲劳寿命，预测结果如表3所示。由表3可知，预测最大相对误差率为3.6%，满足工程精度要求，此误差也小于文献[3]中4.84%的最大相对误差，证明了通过拟牛顿算法优化后的BP神经网络预测连续管疲劳寿命的优越性。

表3 连续管单层疲劳寿命预测结果Table 3 Single layer fatigue life prediction results of coiled tubing

3.2 寿命区间预测

前文通过优化后BP神经网络对连续管疲劳寿命进行了预测。为丰富连续管疲劳寿命研究，本节开展了连续管疲劳寿命区间预测。连续管疲劳寿命区间预测可实现连续管疲劳寿命范围性预测，预测出连续管疲劳寿命的上、下限。

基于前文已有拟牛顿算法优化后BP神经网络预测连续管疲劳寿命结果，提出优化后BP神经网络预测连续管疲劳寿命区间。预测前，先依据已有数据获得连续管疲劳寿命区间预测样本数据，其函数表达如下：

(8)

式中：α和β分别为连续管疲劳寿命区间上限与下限；randi是均匀分布的随机整数函数。

依据式(8)生成连续管疲劳寿命区间训练样本，如表4所示。

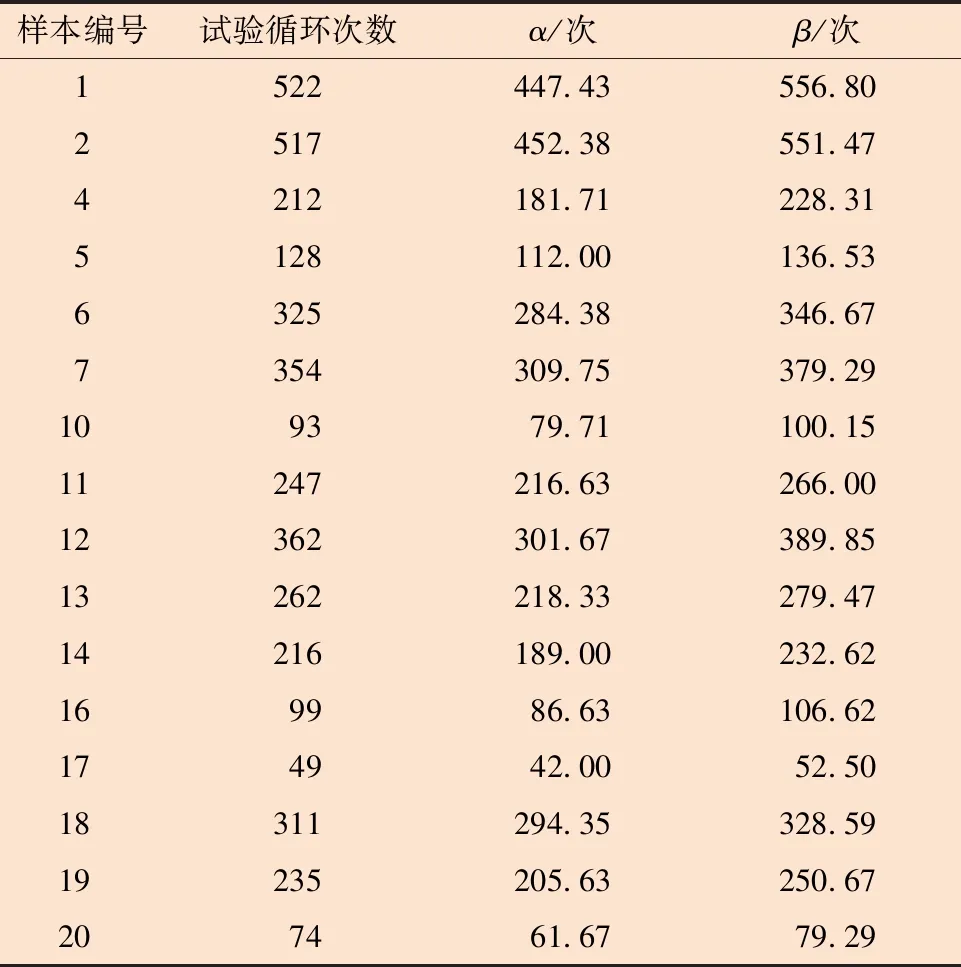
表4 连续管疲劳寿命区间训练样本Table 4 Fatigue life interval training samples of coiled tubing

预测连续管疲劳寿命区间时依据式(7)重新调整网络结构。确定BP神经网络模型结构为4-8-2。通过拟牛顿算法优化后的BP神经网络预测表4中的预测样本寿命区间，预测结果如表5所示。预测结果表明，所有预测样本都落在合理预测范围之内。

4 结 论

(1)拟牛顿算法优化后的BP神经网络预测连续管疲劳寿命时，预测最小相对误差率为1.7%，最大相对误差率为3.6%，满足工程精度要求。

(2)基于拟牛顿算法优化改进后BP神经网络，提出连续管疲劳寿命区间预测，预测结果满足工程精度要求，丰富了连续管疲劳寿命预测方法。

(3)与标准BP神经网络相比，拟牛顿算法优化后BP神经网络预测连续管疲劳寿命时，训练高效且预测精准，避免了容易陷入局部极小值和训练时间过长的问题。