过驱动电动汽车底盘稳定性协调控制

万正宇 李泽彬 赵月 孙国正 丁宗阳

（1.东风汽车集团有限公司技术中心，武汉 442021；2.东风商用车技术中心，武汉 442021）

1 前言

轮毂电机驱动技术因其更快的响应速度、更好的控制性能及更高的控制精度等优点，更具电控的潜力和智能化的优势，更易实现先进底盘动力学协调控制[1-2]。

李胜琴等[3]提出整车横摆稳定性控制和轮毂电机转矩分配控制策略，通过对轮毂电机输出转矩的控制实现了车辆横摆稳定性控制。褚文博等[4]从驱动系统多动作耦合及制约问题入手，提出了2 种多轮驱动转矩协调控制策略。张志勇等[5]基于鲁棒控制理论，设计了基于状态观测的H∞车辆稳定性控制器，将差动制动与差动驱动相结合，提出了基于横摆力矩的转矩分配控制策略。

在车辆实际运行过程中，不同的控制策略切换可能会引起控制输出的剧烈变化，无法保证平稳过渡，且由于电动汽车底盘执行器电子元件较多，容易出现失效故障。现有的研究大多集中在单控制器稳定性控制方面，而没有考虑底盘独立控制器的协调控制，本文基于某前轴单电机集中驱动+后轴轮毂电机驱动底盘，利用分布式驱动电动汽车电机力矩响应迅速及力矩独立可控的特点，通过电子稳定性控制（Electronic Stability Controller，ESC）系统与整车控制单元（Vehicle Control Unit，VCU）及扭矩矢量控制单元（Torque Vector Vontrol Unit，TVCU）的协调控制，保证各类工况下车辆的动态性能及稳定性，并基于实车进行验证。

2 系统仿真模型

2.1 联合仿真模型

基于CarSim 软件构建车身及车辆部分子系统的联合仿真模型，如图1 所示。使用Simulink 轮毂电机模型取代原有动力传动系统，并在后续研究中将轮毂电机视为整体，采用直接转矩控制方式对理想电机模型进行建模。最后通过S函数将CarSim中所建立的四轮独立线控电动汽车模型导入Simulink，组成完整的动力学控制模型，用于验证所提出的稳定性协调控制策略的有效性。

图1 联合仿真模型结构

2.2 电机特性模型

基于某现有前轴单电机集中驱动+后轴轮毂电机分布式驱动底盘所搭载轮毂电机的实测结果，得到电机特性模型，如图2所示。

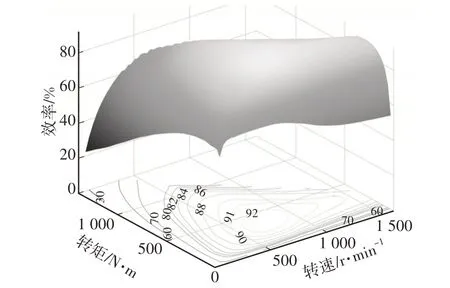
图2 轮毂电机特性MAP图

3 基于PID的底盘稳定性协调控制

根据系统结构，搭建了如图3 所示的基于PID的控制系统模型。其中：二自由度参考模型通过转向盘转角δ及实际车速Vx可以识别出整车的期望质心侧偏角βd及期望横摆角速度γd；质心侧偏角观测器通过实车状态计算出车辆实际质心侧偏角β；失稳程度参数计算模块通过实车质心侧偏角和横摆角速度计算出整车的失稳程度参数η并根据标定阈值θ进入稳定性协调控制模块，计算出车辆所需轮缸压力及四轮期望转矩。

图3 控制系统结构

3.1 二自由度车辆参考模型

车辆的质心侧偏角和横摆角速度对汽车操纵稳定性影响较为明显，因此在车辆行驶过程中需要严格控制两者的大小以防止车辆失稳。以二自由度车辆模型为基础，可计算出期望质心侧偏角及期望横摆角速度：

式中，kf、kr分别为前、后轮侧偏刚度；δf为前轮转角；lf、lr分别为质心到前、后轴的距离；Iz为横摆转动惯量；m为整车质量；ΔMz为附加横摆力矩。

3.2 质心侧偏角观测器

当前，车辆质心侧偏角估计方法包括直接积分法[6]、动力学方法[7]等，考虑到成本及车辆控制的实时性，基于运动学方法设计质心侧偏角观测器：

式中，ax为车辆纵向加速度；ay为车辆侧向加速度；γ为车辆实际横摆角速度。

该方法主要利用ESC 内置的三轴向传感器及车速估计模块，对车辆参数、路面附着系数及驾驶操作带来的整车动力学响应具有较好的鲁棒性。在传感器信号精确的情况下，对处于线性区和非线性区的质心侧偏角都具有较高的估计精度。

3.3 失稳程度参数计算

通过失稳程度参数计算模块判断整车进入何种控制模式。在车辆的稳定性控制中，质心侧偏角与横摆角速度存在耦合影响，所以在计算失稳程度参数η时需要对两者进行加权联合控制：

其中：

式中，Δβ为观测质心侧偏角与期望质心侧偏角的误差；Δγ为实际横摆角速度与期望横摆角速度的误差；Δβ1、Δβ2分别为根据实际运行工况选取的质心侧偏角误差下边界和上边界。

权重系数q与|Δβ|的关系如图4所示。

图4 权重系数取值

失稳程度参数计算过程中，质心侧偏角误差较小时，横摆角速度误差为主要计算量，质心侧偏角误差较大时，质心侧偏角误差为主要计算量，且根据质心侧偏角误差实时计算权重系数。

3.4 车辆状态判断模块

通过失稳程度参数η及失稳程度参数阈值θ将车辆状态分为稳定区、过渡区及失稳区。θ为与车速Vx相关的标定量，车速越大，θ越小，如图5所示。

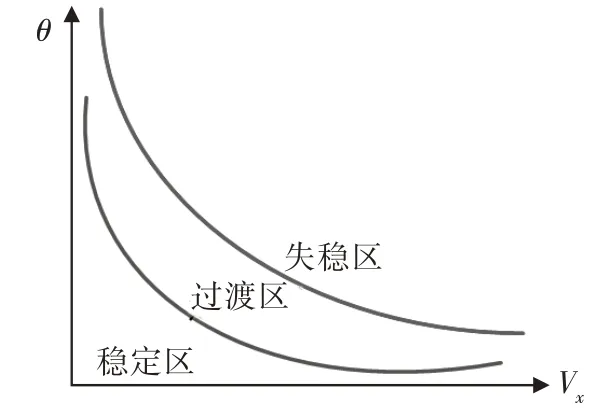
图5 失稳程度参数阈值示意

车辆处于稳定区时，VCU、TVCU 进入1+2 分配（扭矩按比例分配给前、后轴）模式，后轴轮毂电机执行VCU 请求转矩并分配到左、右轮；车辆进入过渡区时，TVCU 进行后轴转矩独立控制，在线性区域改善车辆稳定性；车辆进入失稳区后，ESC系统接管前轴单电机和后轴轮毂电机，VCU 及TVCU 作为执行器执行ESC系统请求转矩。

3.5 稳定性控制模块

横摆力矩控制（Active Yaw Control，AYC）作为ESC 系统的重要组成部分，对保持车辆在极限工况下的稳定性具有重要作用。本文采用分层控制，上层为决策层，根据车辆实际状态计算所需直接横摆力矩ΔMz，下层为转矩分配层，将得到的总力矩合理分配到4个车轮。上层考虑实车控制的鲁棒性及稳定性控制所需实时性，采用PID 闭环控制进行期望横摆力矩的计算；下层根据期望横摆力矩ΔMz、驾驶员期望驱动转矩Td及实际后轮转速，通过建立的轮毂电机查表模型求解最优四轮输出转矩及四轮轮缸压力P。

上层PID控制器决策出的期望横摆力矩ΔMz为：

式中，kp为比例系数；ki为积分系数；kd为微分系数；e(t)为失稳程度参数与阈值的误差绝对值。

下层力矩分配控制以轮毂电机效率为优化目标，可表示为：

式中，J为优化问题函数；c为后轴轮毂电机效率；ωi、Tti分别为轮毂电机实际转速及分配扭矩；d为轮距；r为轮胎半径；Tpi为各轮轮缸压力产生的制动转矩；Tmmax为驱动系统所能提供的最大驱动转矩；Ti为各轮总的驱动/制动转矩；i=1,2,3,4 分别表示车辆左前、右前、左后、右后轮。

式（6）中的约束条件用于满足期望横摆力矩及驾驶员期望转矩。对式（6）所示的有约束非线性规划问题，采用MATLAB自带工具箱函数中的fmincon命令求解。

4 仿真分析

为验证所提出的稳定性协调控制算法在各类工况下的有效性，通过CarSim 与Simulink 联合仿真，选择低附着系数单移线工况进行验证。设定初始车速为80 km/h，路面为雪面，路面附着系数为0.4，在第2 s 时驾驶员输入幅值为60°的转向盘正弦转角，仿真结果如图6所示。

图6 单移线工况车辆动力学响应

从图6b～图6f 中可看出：无稳定性协调控制时车辆在短时间内即冲出车道，无法跟随期望路径，且动力学响应较为剧烈；增加稳定性协调控制后，在过渡区通过后轴扭矩控制可以保证车辆的稳定性，在失稳区ESC 系统介入，扭矩控制和液压控制共同作用，维持车辆的稳定行驶。

5 实车验证

选择均一低附着系数（雪面）双移线工况进行实车验证，初始车速为60 km/h，验证结果如图7所示。

图7 双移线工况实车动力学响应

从图7b～图7d 中可看出，在稳定性协调控制介入后，车辆在激烈工况下的动力学响应较为稳定，且转矩控制和液压控制的衔接较为平稳。

6 结束语

本文提出一种电动汽车底盘稳定性协调控制方法，仿真测试与实车验证结果表明，二者车辆动力学表现一致，表明该策略能够较好地保证车辆在稳定区和过渡区的通过性及失稳情况下的稳定性，并可较好地平衡不同控制策略切换带来的剧烈变化，充分发挥轮毂电机驱动底盘的先进性。