重尾噪声环境下的扫描雷达稳健角超分辨方法

张 寅 张永超2， 晏家楠 刘帅迪 杨建宇

（1.电子科技大学信息与通信工程学院，四川成都 611731；2.电子科技大学长三角研究院（衢州），浙江衢州 324000）

1 引言

扫描雷达具有快速重访和广域成像能力，且能适应任意成像构型，在飞行器复杂地形回避、自主着陆、地物信息侦察感知、海面搜索与救援等领域有着重要的应用价值［1-4］。在距离向上，扫描雷达可通过发射宽带信号并通过匹配滤波技术实现距离向高分辨。在方位向上，由于平台天线孔径的限制，其方位角度分辨率远低于距离分辨率［5-6］。如何突破天线物理孔径的限制，提升扫描雷达角分辨能力，已成为实际应用中亟待解决的难点问题。

扫描雷达波束掠过目标的过程可以建模为雷达波束天线方向图与目标散射系数间的卷积关系。因此，反卷积方法可以用于扫描雷达以提升角分辨率。文献［7］中提出了一种广义逆滤波反卷积方法，可用于提升扫描雷达角分辨率。文献［8］中提出了改进维纳滤波反卷积方法，并实测数据处理结果验证了方法的有效性。文献［9-11］中将经典的Lucy-Richardson 方法拓展于雷达扫描波束超分辨成像应用中，有效提升了扫描雷达角分辨能力。文献［12］基于不同最优化准则，分别研究了高斯分布下的基于贝叶斯准则的统计优化方法，以及基于最大熵的统计优化方法，并采用实测数据验证了有效性。然而，上述反卷积方法均依赖较高的信噪比，在低信噪比时易出现虚假目标。

近些年来，阵列信号处理方法被广泛应用于扫描雷达成像。文献［13］通过假设天线方向图与阵列信号空间导引矢量之间的映射关系，采用正则化Capon 算法，实现了机载扫描雷达角超分辨成像。该方法在高信噪比条件下，能够实现较好的超分辨成像性能。文献［14］通过构建传感器阵列，在雷达前视成像中引入阵列信号处理技术，提出一种改进的正则化多重信号分类（MUSIC）算法，仿真结果验证了该算法能够有效提高雷达图像在前视方向上的方位角分辨率。但是，Capon和MUSIC依赖于大量快拍数据，这种条件在扫描雷达成像过程中难以满足。文献［15］提出一种迭代自适应方法（IAA），该方法能够适用于少量甚至单次快拍数据。文献［16-17］将IAA应用于扫描雷达超分辨领域，并提出了一种频域快速IAA，将矩阵求逆运算转化为循环矩阵-向量快速乘积运算，解决了IAA的高效计算难题，实现了机载扫描雷达前视超分辨快速成像。文献［18］建立了基于辐射-天线方向图的扫描雷达相干信号模型，并提出了基于相干信号模型的IAA 超分辨方法，其角分辨性能相比非相干信号模型有明显提升。

天线方向图与目标散射系数间的卷积过程也可以用线形观测方程模型描述，其中观测矩阵为天线方向图构成的循环矩阵。因此，扫描雷达角超分辨可以采用逆方法实现。然而，由天线方向图构成的循环矩阵为一病态矩阵。正则化方法通过在目标信号重建模型中引入惩罚项，使用一个近似良态问题代替原始的病态问题。相比上述两类超分辨算法，正则化算法具有正则化约束可灵活调节的优点，可根据目标场景的分布特性，灵活地选取目标项约束，例如平滑约束（l2-l2）、稀疏约束（l2-l1）、边缘约束（l2-TV）等。文献［19］中提出了基于Tikhonov正则化的角超分辨方法，它通过引入l2范数正则化项，在提高分辨率的同时显著抑制了噪声的放大。然而，该方法存在过平滑问题，导致其对分辨率的改善极为有限。文献［20］中提出一种基于梯度直方图维持的超分辨成像方法，在Tikhonov 正则化的基础上引入了待复原场景的梯度分布。该方法在抑制噪声放大的同时进一步提高了分辨率。文献［21］中提出一种全变差（Total Variation，TV）正则化的角超分辨方法，该方法通过在正则化框架下引入TV 范数约束实现目标轮廓重建，但对于孤立目标无法实现分辨能力提升。实际应用中，场景内目标的分布通常具有稀疏特性。文献［22］中提出一种联合TSVD与l1范数正则化约束的超分辨成像方法，将截断奇异值分解（TSVD）与l1范数约束相结合，进一步提升了角分辨能力。文献［23］中为了解决噪声抑制与角分辨率之间的矛盾，改进了传统l1正则化方法，提出一种混合l1-l2正则化超分辨率方法。与现有反卷积和阵列信号处理方法相比，基于稀疏先验的正则化方法能够获得更高的角分辨能力。

然而，现有的基于稀疏先验的正则化方法中，通常假定扫描雷达成像面临的噪声服从高斯分布，然而在实际应用中，扫描雷达在现实环境中遇到的噪声通常会存在大幅度尖峰异常值，在时域表现出较为明显的脉冲特性［24］，例如低频大气噪声、自然界中闪电雷暴产生的电磁干扰、来自敌方电子干扰机的脉冲干扰等［25］。这些噪声出现的方式几乎都是瞬时的并且持续时间非常短暂，它们的特点是幅值大、无规律、不连续。这类干扰噪声在概率分布上会表现出比较严重的拖尾现象，即概率分布曲线的尾部趋向于零的速度相较于高斯分布来说更加地缓慢，通常将这种重尾分布的脉冲噪声称为重尾干扰［26］。

针对这一问题，本文提出一种重尾噪声条件下的扫描雷达角超分辨成像方法。该方法首先引入一种最小绝对偏差（LAD）-LASSO 约束准则以抑制重尾分布噪声；更进一步的，针对模型中存在的正则化参数自适应选取难题，本文基于稀疏自相关迭代准则导出正则化参数的最优表达。最后，针对LAD-LASSO 非平滑代价函数最优化求解难题，提出一种基于迭代重加权最小二乘（IRLS）算法的求解方法，通过将l1范数替换为重加权的l2范数，并在每次迭代中进行权值更新实现最优求解。仿真和实测数据结果表明，本文提出的方法能够在提升扫描雷达角分辨率的同时有效抑制重尾分布噪声。

2 扫描雷达回波模型

扫描雷达通过发射线性调频信号并采用波束扫描方式对目标区域进行成像，成像的几何模型如图1所示。

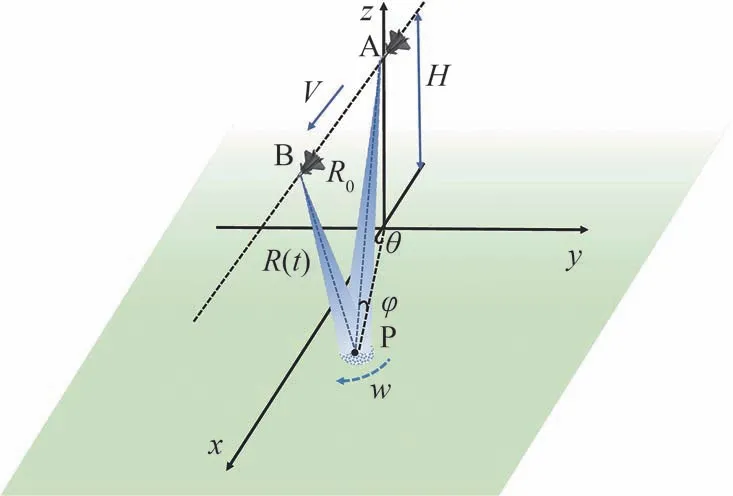
图1 机载扫描雷达的几何模型Fig.1 Geometric structure of airborne scanning radar

图2 重尾噪声和高斯白噪声概率分布曲线对比图Fig.2 Comparison of heavy-tailed noise and Gaussian white noise probability distribution curves

以机载平台为例，假设飞机初始位于点A，以速度V沿某一方向飞行，飞行高度为H，天线的扫描角速度为w。扫描场景中有一点目标P，其相对于雷达的初始斜距为R0，方位角为θ0，俯仰角为φ0。在经过时间t后，飞机到达B点，此时飞机与点目标的斜距为

其中a0为点目标与雷达的初始前视角。通过泰勒展开以及忽略二次项后，（1）可以近似简化为：

假设发射的线性调频信号可以表示为：

其中rect(·)为矩形窗，Tp为脉冲宽度，τ为距离向时间，fc为载频，K为调频率。点目标P 的回波经过下变频后表示为：

其中，σP表示目标后向散射系数，h(·)为天线调制函数，τd=2R(t)/c为双程回波时延，c为光速。

在对接收的回波信号进行脉冲压缩和距离徙动校正处理后，回波信号可以表示为：

其中B为线性调频信号的带宽，sinc(·)为脉冲压缩之后的信号包络。将（5）转换到距离-角度域，并考虑整个扫描区域的回波信号，可以得到

其中M与N分别为扫描区域中距离向与方位向的采样点数，λ为信号的波长，为多普勒频移，通常可以被忽略。因此回波信号可以建模一个卷积的形式：

式（7）中y(R，θ)为接收信号，h(R，θ)为天线方向图函数，σ(R，θ)为目标散射系数，n(R，θ)为加性噪声，⊗为一维卷积运算符号。

式（7）在离散化后可以写为矩阵的形式：

其中y∈CN*1与s∈CK*1分别表示为第m个距离单元的接收信号与目标散射系数，K为原始场景中同一距离单元方位向的采样点数，n∈CN*1为加性噪声向量，A∈CN*K为天线方向图调制矩阵，其可以表示为

其中[h(θL)，h(θL-1)，…，h(θ1)]为方位向天线方向图的采样点。L为天线方向图的采样点数。

重尾噪声可以用各向同性独立同分布的高斯混合模型来描述：

3 基于LAD-LASSO的稀疏角超分辨方法

3.1 LAD-LASSO准则

实际应用中受关注的目标，如地面装甲集群、海面上的舰船编队、空中的战机编队等，在雷达图像中仅体现为若干强点，且在整个场景中只占很小一部分，因此成像场景呈现典型的稀疏特性，即s∈CK*1是稀疏的。最小绝对收缩和选择算子（LASSO）回归方法在正则化框架中引入稀疏范数，即采用l1范数来表征目标的稀疏特性，将扫描雷达角超分辨问题转换为如下约束优化问题［27］：

其中λ为正则化参数，‖·‖1为l1范数。上式中的第一项，即残余项主要通过l2范数约束。在高斯白噪声假设下，该约束能够有效抑制噪声。然而，这一约束对重尾噪声比较敏感。在重尾噪声条件下，最小绝对偏差（LAD）能够获得比最小二乘更稳健的参数求解结果。将LAD 与LASSO 相结合，即在LAD损失函数的基础上添加l1范数稀疏约束，能够在对稀疏目标高分辨率重建的同时，有效抵抗重尾噪声的效果［28］，即

3.2 最优正则化参数选取

上述模型中引入了人工参数λ，实际中参数的选择会影响参数估计的效果并且很难调节。针对这一问题，定义目标函数为［29］：

（19）中的惩罚项是加权的l1范数，这种惩罚往往使其解稀疏，然而惩罚并不能区分信号项和噪声项。因此，最小化解（19）也将导致噪声方差的解趋于稀疏。在这种情况下，协方差矩阵R不是满秩的，这将导致模型阶数的估计增加等问题［30］。为了解决这些问题，基于（19）中的约束项的改进，提出了一种广义SPICE算法，即qSPICE算法：

我们首先给出以下引理［31］，这将有助于之后的推导。

引理1：对

其中，最小值解出现在

使用引理1，可以将（22）表示为

对（31）求解得到

对（31）关于σk微分并将其设置为零，我们有

将（34）插入（33）得到

最后，将（32）和（35）插入（31）得到

从（36）中可以注意到，令r=1，q=1，我们有

可以看出，式（14）等效成为一种自适应参数的加权LAD-LASSO形式模型，不需要任何用户参数。

3.3 迭代重加权最小二乘求解

式（37）所示的优化问题中，l1范数存在不可导点，无法直接通过求导得到。因此，基于迭代加权最小二乘（IRLS）的思想，本论文将l1范数的求解问题转化为l2范数的求解。对（37）所示的问题。令。定义如下加权矩阵［32］

那么式（37）可以表示为

由式（40）容易得到加权最小二乘解为

算法流程如表1所示。

表1 本文提出的基于迭代重加权最小二乘的LAD-LASSO求解算法流程Tab.1 The flow chart of LAD-LASSO algorithm based on iterative weighted least squares proposed in this paper

4 仿真结果

4.1 点目标仿真

在本小节中，通过设置一维点目标来验证提出方法在重尾噪声干扰下的成像性能。仿真所使用的参数如表2所示。一维的点目标场景如图3（a）所示，其中在相同的距离单元分别在-1.5°、1.5°的角度位置设置了幅度分别为1，0.5的两个点目标。仿真中使用由各向同性独立同分布高斯混合模型描述的重尾噪声，仿真实验中设置的信噪比为20 dB，受到重尾噪声污染的回波如图3（b）所示。可以看出，在实波束回波无法对目标进行区分，且出现明显的毛刺，这符合重尾噪声特点。图3（c）～（f）分别给出了基于LASSO 的角超分辨方法、IAA 方法、Lucy-Richardson（L-R）方法以及本文提出方法的成像结果。其中在每张图中显示了10 次Monte-Carlo试验的结果。可以看出，受到重尾噪声影响，传统的超分辨方法均无法有效的分辨目标，而本文提出的方法能够很好的分辨出两个点目标，证明了提出算法的有效性。

表2 仿真参数Tab.2 Simulation parameters

图3 重尾噪声下的仿真结果Fig.3 Simulation results under heavy-tailed noise

为了量化和比较重尾噪声下的不同方法成像性能，本节中使用了方位角度位置平均偏差作为指标，表示为：

其中，N为估计的目标个数，与θ1分别表示估计的目标方位角度与目标真实方位角度，试验重复10次，即M=10，对全部试验的角度偏差取均值作为结果。在同一信噪比下，AE 越小则说明方法在重尾噪声下的分辨性能就越好。不同信噪比的重尾噪声下的传统方法与提出方法的方位角度位置平均偏差如图4 所示，从中可以看出在不同信噪比的重尾噪声下提出方法的超分辨成像性能均优于传统方法。

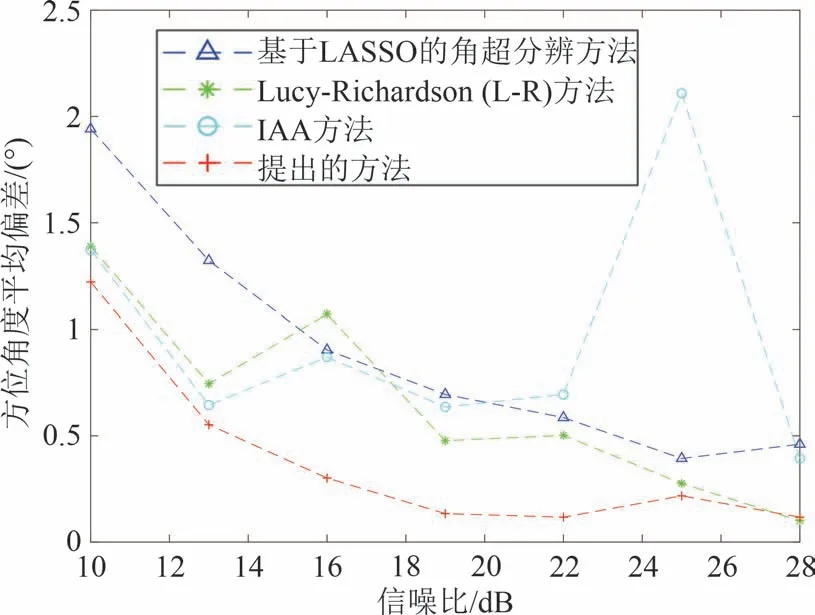
图4 不同信噪比下不同方法估计方位角度的平均偏差对比Fig.4 Comparison of the average deviation of the estimated azimuth by different methods with different signal-to-noise ratios

4.2 实验数据

本小节使用在固定雷达平台上获得的真实数据集进一步证明所提出的方法在受到干扰影响下的成像性能。雷达真实数据集来自于岸基雷达对重庆江面船只的观测，如图5（a）所示。在我们的实验中，受害雷达是连续波雷达。受害雷达的系统参数列于表3 中。干扰雷达为非合作雷达，工作于河流及周边地区，系统参数为非合作且未知。

表3 系统参数Tab.3 System parameters

图5 实测数据处理结果Fig.5 Processing results of real-data

在实验中，雷达系统受到了来自未知辐射源的随机干扰信号的脉冲干扰，可以视作雷达回波受到由加性高斯白噪声及嵌入其中的脉冲噪声组成的重尾噪声干扰。对重尾噪声干扰下的此数据集进行超分辨会造成多种影响，例如重建图像中会产生虚假目标，分辨率降低或者目标位置存在偏差等。图5（b）为原始回波数据经脉冲压缩处理之后的结果，从图中可以很明显的看出实波束回波中出现了无意的干扰。这里重点关注用红色圆圈标记的两艘船的分辨，这两艘船的位置相隔很近，从图中可以看出在通过脉冲压缩处理后无法从实波束回波中分辨目标。图5（c）～（e）分别给出了使用基于LASSO的角超分辨方法、IAA方法、Lucy-Richardson（L-R）方法处理之后的结果，可以从图中看出，干扰依然存在且无法分辨目标。图5（f）为使用提出的超分辨成像方法处理之后的结果，从图中可以看出干扰极大的衰减，且分辨率得到了明显的提高，两只船可以容易的被分辨出来，证明了提出算法的有效性。

为了进一步对比方法性能，图6 展示了图5 中标有红圈的相邻船只的方位角切面图。如图6 所示，可以明显看出，实波束回波与使用基于LASSO的角超分辨方法、IAA 方法、Lucy-Richardson（L-R）方法处理后均无法分辨相邻目标，而使用本文提出的方法处理后可以看出分辨率得到了明显的提高，这证明了提出算法的有效性。

图6 图5所示结果中的方位剖面对比结果Fig.6 Results of azimuth profile comparison in the results shown in Fig.5

5 结论

本文提出一种重尾噪声条件下的扫描雷达抗角超分辨成像方法。为抑制重尾分布噪声，该方法首先引入了LAD-LASSO约束准则，并导出了正则化参数的最优表达；同时，本文提出一种基于IRLS 算法对LAD-LASSO非平滑代价函数进行最优化求解。仿真和实测数据结果表明，本文提出的方法能够有效抑制重尾分布噪声，并有效提升扫描雷达角分辨率。