单频涡旋电磁波雷达旋转目标微动参数提取方法
罗 迎 袁 航 袁延鑫
(1.空军工程大学信息与导航学院,陕西西安 710077;2.复旦大学电磁波信息科学教育部重点实验室,上海 200433)
1 引言
近年来,涡旋电磁波在通信领域和雷达领域受到了广泛关注,针对涡旋电磁波的产生、传输和应用的研究也取得了大量的进展[1-3]。与传统电磁波[4]不同,涡旋电磁波携带轨道角动量(OAM,Orbital Angular Momentum),其波前相位结构呈螺旋形[5],且不同OAM 模态的涡旋电磁波相互正交[6]。对于传统电磁波,雷达和目标之间的径向相对速度会引起线多普勒效应[7],利用该效应可获得目标径向微动信息,已广泛应用于目标识别与微动参数提取领域[8-10]。但线多普勒效应仅含有目标沿雷达视线(LOS,Line of Sight)的运动信息,基于线多普勒效应的微动参数估计方法仅能获得目标径向微动参数。当利用涡旋电磁波照射目标,回波中不仅含有径向相对速度引起的线多普勒效应,还含有垂直径向相对速度引起的角多普勒效应[11]。若将涡旋电磁波应用于旋转目标微动参数提取领域,则可提取目标的真实旋转半径和倾斜角等特征[12]。
迄今为止,涡旋电磁波已被应用于诸多领域中,如二维高分辨率成像[13]和低信噪比(SNR,Signal to Noise Ratio)成像[14],然而基于涡旋电磁波雷达的微动参数提取仍处于发展阶段。文献[12]率先研究了涡旋电磁波雷达旋转目标多普勒效应和微多普勒效应,并推导了旋转目标的角多普勒频移公式,给出了特殊情况(倾斜角为0或旋转中心位于Z轴上)下的微动参数提取方法,但未讨论线多普勒和角多普勒的分离问题和任意情况下的微动参数提取问题。
文献[15]基于传统平面波雷达回波和涡旋电磁波雷达回波间的多普勒频移差异,利用时频工具提取两者的多普勒频移曲线,通过曲线差值提取目标角多普勒频移,最后利用Hough 变换估计目标二维微动参数(旋转半径、倾斜角)。但此类方法对线多普勒和角多普勒的分离是基于不同模态多普勒频移曲线的相减,对线多普勒和“线+角”多普勒的频移曲线的估计会使实际多普勒曲线被量化,两个量化后的曲线相减会导致误差进一步扩大。同时,当目标由多个散射点组成时,估计角多普勒前需分离多条时频曲线,散射点越多时曲线分离越为困难。且在角多普勒的影响下,线多普勒时频图与“线+角”多普勒时频图的能量分布不同,难以直接将线多普勒时频图的曲线分离结果套用到“线+角”多普勒时频图中。因此该场景下的时频曲线匹配是此类方法需要解决的一个问题。文献[16]重点研究了雷达前视条件下的锥体目标参数估计利用锥体微动对回波瞬时频率的周期性调制特性,反演出锥体目标的微动参数和几何特征,但该文献的研究场景为雷达前视成像,与本文场景不同,难以直接应用。
为解决上述问题,提出了一种能够适用于角多普勒较小、目标旋转中心未知场景下的单频涡旋电磁波雷达旋转目标微动参数提取方法。首先,基于线多普勒时频图获得目标径向微动参数;在此基础上构建补偿函数补偿涡旋电磁回波,并利用滤波方法去除补偿后的信号中的干扰项,获得较为纯净的角多普勒信号;随后,利用径向微动参数和角多普勒极值点间隔等信息构建多个微动参数间的关系式,使对四维参数空间的搜索变为一维向量上的搜索,在获得目标微动参数的基础上降低了计算量。
2 单频涡旋电磁波雷达旋转目标回波模型
单发多收的涡旋电磁波产生模型如图1 所示。K个阵元等间距排列在半径为a的圆环上,第k个阵元与X轴正半轴的夹角为φk。
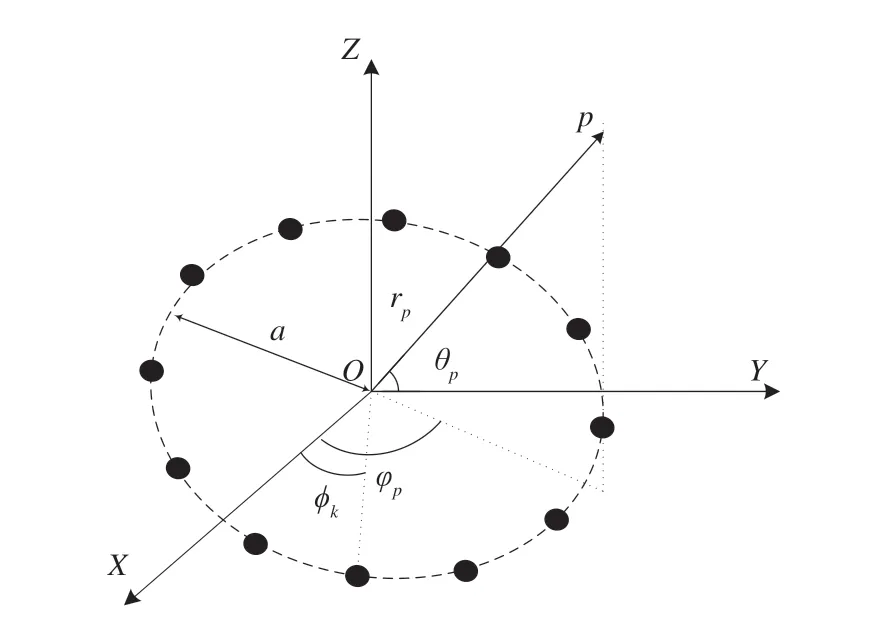
图1 雷达与目标的几何关系Fig.1 The geometry of radar and target
发射天线位于空间直角坐标系OXYZ的原点O,发射单频信号
式中:t为时间,fc为载波频率。信号照射球坐标为(rp(t),θp(t),φp(t))的第p个散射点,第k个阵元接收的回波为sp(t,k)
式中:σp为散射系数,时延τp,k(t)=(2rp(t)-asinθp(t)cos(φk-φp(t)))/c,c为光速。设模态数为α,对每个阵元添加相移exp(iαφk)并求和,获得涡旋电磁回波
式中:“·”为乘法符号,Jα()为第一类α阶贝塞尔函数,kc=2πfc/c,τp(t)=2rp(t)/c。去除载频和常数项后,回波重写为
与传统平面波相比,涡旋电磁回波的相位项exp(iαφp(t))中蕴含目标方位角信息,通过分析该相位项,可获得目标垂直于径向上的微动分量信息。但相位项exp(iαφp(t))的引入也增加了回波模型的复杂度,需要针对不同类型目标推导新的回波模型。下面针对旋转目标进行分析,给出旋转目标回波模型。假设旋转半径为rb,倾斜角(旋转平面与XOY平面的夹角)为θb,旋转频率为fb,旋转中心为(xb,yb,zb),θc为雷达视线方向。为便于分析,将一平行于XOY平面的旋转目标,经三维旋转后变为所需分析的目标。目标三维旋转会改变距离变化的幅度和初相。但在不考虑初相改变的前提下,三维旋转结果可由一个特定的一维旋转表示,即目标经一维旋转特定的角度后可获得与三维旋转相同的距离变化幅度。只需考虑倾斜角对三维旋转矩阵Rinit的影响,可将Rinit写为
第p个散射点随时间t的直角坐标变化可表示为
将上式展开得到
转换到球坐标系后,可写为
式 中:φb=arctan((ybcosθb+zbsinθb)/xb),φp为第p个散射点的初相,,arctan()为反正切函数。旋转会导致散射点与雷达平台间的距离以余弦函数的规律变化,其幅度即为径向半径rbsin(θb+θc)。将式(8)代入式(4),即可获得单频涡旋电磁波雷达中旋转目标的回波模型。由式(8)中rp(t)变化引起的多普勒频移为线多普勒,载频越高线多普勒越大,但与涡旋电磁波模态数无关。同理可得由式(8)中φp(t)变化引起的多普勒频移为角多普勒,模态数越高角多普勒越大,与载频无关。
3 角多普勒提取方法
针对线多普勒和角多普勒分离问题,现有方法大多使用时频分析方法,基于同一散射点回波的角多普勒瞬时频率在不同模态下存在差异的原理,通过图像处理方法分离线多普勒和角多普勒,但受限于时频分析方法的频率分辨率,时频分析方法难以适用频率差较小的场景。如图2所示的理想旋转点目标时频图,(b)中的角多普勒与(a)中的线多普勒叠加,导致(c)中的总的“线+角”多普勒时频曲线发生轻微变化,但即使在角多普勒较大的情形下,总多普勒的时频图像仍与线多普勒较为相近,当角多普勒较小时,基于时频图像的角多普勒曲线提取方法精确度难以保证。同时还需考虑旋转目标由多个散射点组成时,多条时频曲线的叠加干扰使时频图像难以辨认,曲线分离更为困难。且在角多普勒的影响下,线多普勒时频图与“线+角”多普勒时频图的能量分布不同,难以直接将线多普勒时频图的曲线分离结果套用到“线+角”多普勒时频图中。
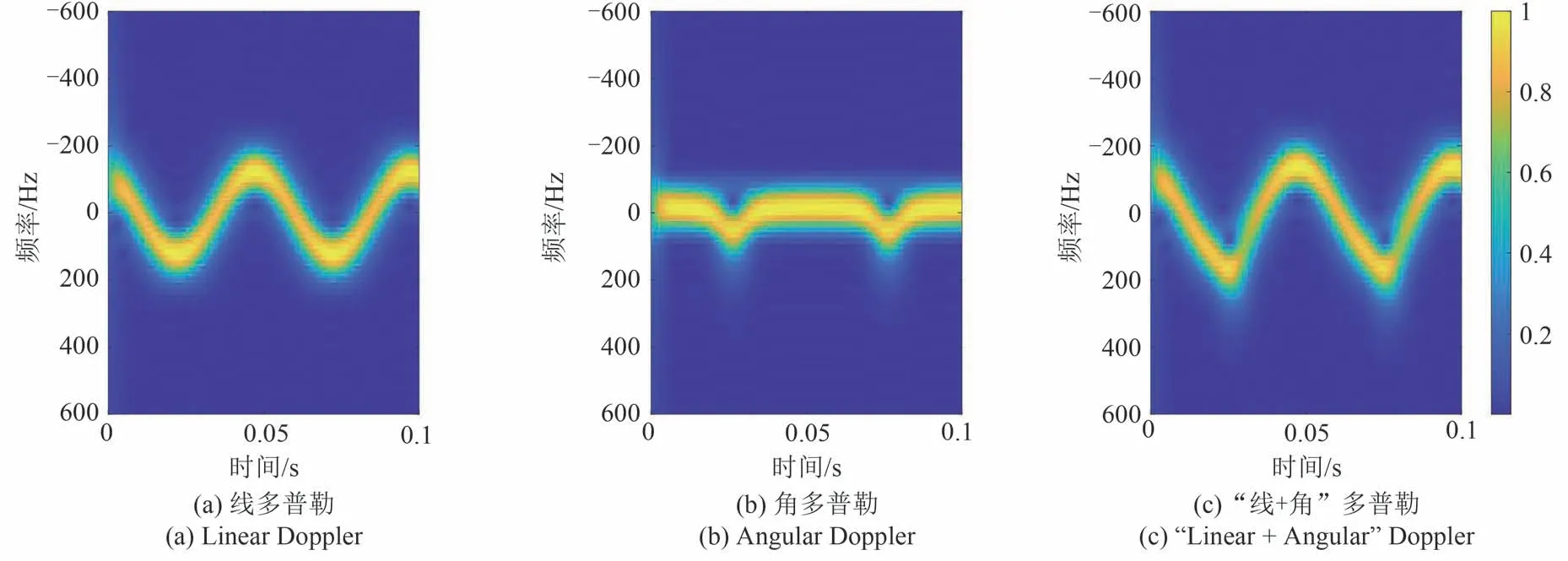
图2 多普勒时频图Fig.2 Doppler time frequency diagram
理论分析可知,线多普勒是由目标距离变化所引起的,与模态数无关;角多普勒由目标方位角变化引起,且与模态数之间存在线性关系。由于线多普勒和角多普勒的时变特性,需对每个时刻的线多普勒进行补偿,从而获得纯净的角多普勒信号。单个时刻的双模态涡旋电磁回波信号中目标距离为固定值,目标方位角与模态数耦合,多普勒信号的实部表现为多个初相不同的余弦函数(在频域混叠时则表现为混叠余弦函数)叠加的形式,若线多普勒已知,此时角多普勒将导致线多普勒信号相位的变化,线多普勒和角多普勒分离问题可被抽象为余弦函数的初相估计问题。
当拥有多个独立维度的信息时,可利用求解矩阵乘法的方式获得余弦函数初相(即角多普勒信号)。但针对单频回波,难以联立多维度回波矩阵分离角多普勒信号,所以利用滤波的方法近似消除较大的线多普勒信号,获得较为纯净的角多普勒信号。由于误差对相位估计的影响较大,所以先将相位中的角多普勒信号变换到幅度中,其过程可描述为
此时,角多普勒信号的实部和虚部调制在幅度中。由于目标尺寸通常远小于目标距离,可近似认为目标的俯仰角等于雷达视线方向,此时贝塞尔函数项为一固定的值。补偿贝塞尔函数后,式(9)可重写为
考虑到多散射点的影响,假设旋转目标由P个散射组成,式(10)可重写为
提取角多普勒信号需利用到线多普勒信息。可针对单个阵元接收的回波进行分析,通过时频变换获得线多普勒时频图像,并利用图像处理方法(如Hough变换)估计目标微动参数。基于线多普勒的微动参数估计方法已较为成熟,在本文中不过多赘述。由线多普勒信号可估计目标旋转频率和径向半径。同时,可利用相关法估计线多普勒信号中的时延φb,获得估计值。由此可生成参考信号
将参考信号与scos(t,α)相乘,获得scos2(t,α)
若各项的估计精度较高,第q个散射点的线多普勒项被消去,可将scos2(t,α)写为
为从scos2(t,α)中分析线多普勒项对线-角多普勒分离的影响,将相位项中的展开,当径向半径和旋转频率估计精度较高时可获得
由于三角函数的独特性质,两个频率相同、初相不同的三角函数相减,其结果的频率不变,幅度受相位差调制。角多普勒调制在幅度不一的线多普勒信号上,scos2(t,α)的时频图如图3所示。图3中在零频处有一条随时间变化的曲线,该曲线即为散射点q的角多普勒信号。同时时频图中存在多个幅度不同的正弦曲线,这些曲线为补偿操作引入的干扰项。若能消除这些项,则可获得旋转目标上散射点q的角多普勒信号。
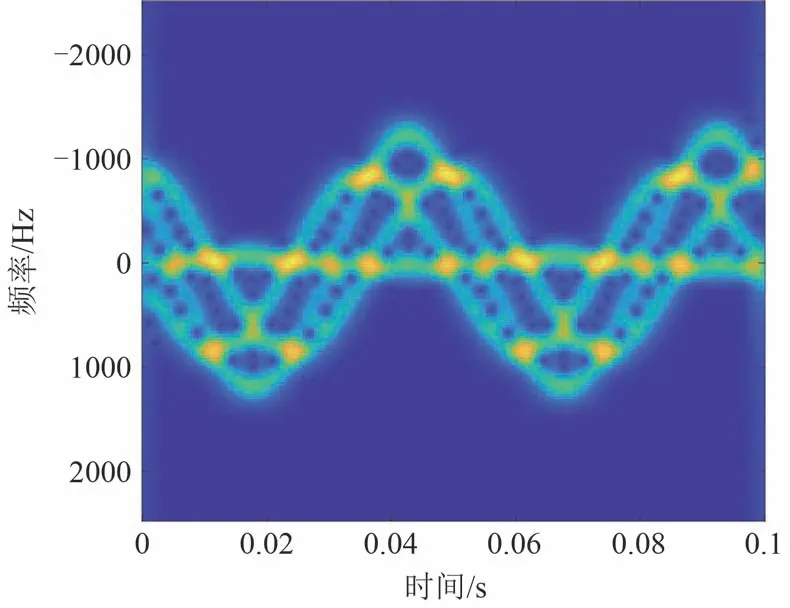
图3 补偿后的时频图Fig.3 Time frequency diagram after compensation
由于干扰项与散射点q的角多普勒信号频率差较大,即干扰项能量集中于高频处,可以通过滤波的方法滤除干扰项。由于均值滤波可有效滤除高频信号,保留低频信号,所以本文中使用均值滤波对scos2(t,α)进行处理,获得scos3(t,α)。至此我们获得了散射点q的角多普勒信号的实部。同理,重复上述步骤后可获得含有散射点q的角多普勒信号的虚部,将两者组合可获得散射点q的角多普勒。
4 微动参数提取
在获得角多普勒信号的基础上,需要对信号进行分析,并将获得的信息与径向半径、旋转频率等微动参数联立,获得目标旋转半径、倾斜角信息,从而获得目标全面的微动参数。
散射点p的角多普勒频移为
由于可通过时频图估计Δt,将式(17)变形后获得
由于目标旋转中心未知,难以利用式(18)估计目标旋转半径和倾斜角。若直接利用压缩感知算法对目标微动参数进行匹配,需在旋转半径、倾斜角、旋转中心坐标xb和yb组成的四维空间中搜索局部最大值,算法运算量较大。此时需要利用先验信息降低搜索维度数目,降低计算量。利用线多普勒估计的目标径向半径rbsin(θb+θc),结合已知的雷达视线方向,可构建径向半径和倾斜角之间的关系式
由式(21)可获得φ与倾斜角θb之间的关系,从而利用φ表示θb。至此,利用先验知识和已获得的信息,将四维空间的搜索变为一维向量上的搜索,其过程可概述为:首先根据线多普勒和角多普勒时频图,估计径向半径、极值点间隔Δt和旋转频率;其次,构建遍历φ的字典Dφ,利用式(21)获得与字典对应的倾斜角,利用式(20)获得与字典对应的旋转中心坐标,利用式(19)和(21)获得与字典对应的旋转半径;最后根据上述信息构建角多普勒回波矩阵D,利用压缩感知算法进行匹配,获得准确、全面的微动参数。由于将四维空间的搜索变为一维向量上的搜索,极大的降低了计算量,其搜索过程较快。本文中使用正交匹配追踪[18](OMP,Orthogonal Matching Pursuit)算法进行搜索。
由于本文中利用正交匹配追踪算法对目标参数进行搜索,所以主要讨论参数空间维度增长对正交匹配追踪算法计算量的影响。对于该算法,其计算量主要集中在矩阵乘法中。设该算法的字典大小为m1×m2,则待搜索范围的大小为m1× 1,信号大小为m2×1,此时矩阵和向量的乘法的计算量为O(m1m2)。文献[15]利用旋转坐标作为先验信息,结合从线多普勒中提取的旋转频率和径向半径,对目标旋转半径和倾斜角进行估计。为便于比较,假设文献[15]同样利用正交匹配追踪算法搜索目标参数。在实际场景中,通常可利用测距和测角技术获得目标与雷达间的距离c和俯仰角θc,目标的旋转坐标往往是未知的。在旋转坐标未知的情况下,文献[15]方法需要针对四维参数(旋转中心坐标xb和yb、rb、θb)进行搜索。设定各维度的搜索长度均为K,则四维参数搜索的长度为K4。计算量为O(K4m2)。若利用先验信息(目标与雷达间的距离和俯仰角)对四维参数空间降维,即利用c和θc表征旋转中心坐标xb和yb。则文献[1]中方法需在三维参数空间(φ、rb、θb)中搜索,其计算量为O(K3m2)。而所提算法利用角多普勒获得φ、rb和θb间的关系,将四维参数空间中的搜索变为一维向量上的搜索,其计算量为O(Km2)。
至此实现了在角多普勒较小、旋转中心未知场景下的角多普勒信号的提取与微动参数的估计,其算法框图如图4所示。
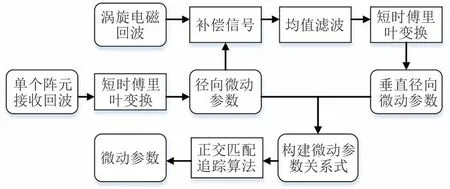
图4 算法框图Fig.4 Algorithmic flowchart
5 仿真与分析
为验证算法有效性,在本节中设置了多个仿真,从多个角度对算法进行分析。雷达参数如表1所示。涡旋电磁波雷达发射频率为3 GHz、持续时间为0.1 s 的单频信号照射目标,回波采样率为5 kHz。多个阵元接收回波后,利用单发多收装置的特性获得模态数为5的涡旋电磁回波。

表1 雷达参数Tab.1 Radar parameters
目标微动参数如表2 所示,旋转目标的旋转频率为20 Hz、旋转半径为0.3 m、旋转中心为(0.4,0.4,200)m、倾斜角为0.9 rad。旋转目标由均匀分布在同一圆环上的4个等散射系数的散射点组成。
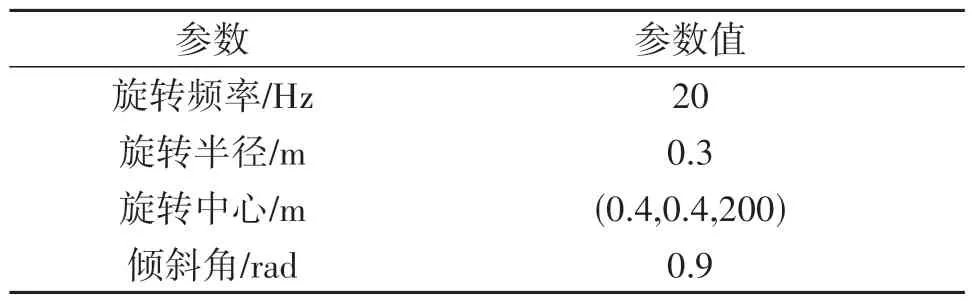
表2 目标参数Tab.2 Target parameters
分别基于单个阵元获得的平面电磁回波和多个阵元累加获得的涡旋电磁回波,利用短时傅里叶变换获得目标线多普勒时频图和“线+角”多普勒时频图,如图5 所示。图5(a)为旋转目标线多普勒时频图,由于多个散射点的存在,目标时频图出现了多条时频曲线,不同曲线的相互叠加为分析增添了难度。图5(b)为旋转目标“线+角”多普勒时频图。

图5 目标时频图Fig.5 Target time-frequency diagram
与图5(a)相比,(b)中时频曲线和能量分布发生变化,其原因在于角多普勒使不同时频曲线叠加后的能量分布发生变化,导致“线+角”多普勒时频图与线多普勒时频图存在一定差异。该差异会导致(a)和(b)的时频图像骨架提取结果存在较大差异,且难以将多个散射点在两者时频图中的曲线一一对应。图5中旋转目标时频图的骨架提取结果如图6所示。图6(a)为线多普勒时频图骨架提取结果,由于散射点较多,不同时频曲线相互干扰使骨架提取结果不理想。图6(b)中的时频曲线较为规律,曲线在零频附近较为光滑,但在频率极值处波动较大。由于角多普勒引起的时频图能量分布变化,两者的时频图骨架提取结果不同,多个散射点的时频曲线分离难度较大,线多普勒时频图曲线与“线+角”多普勒时频图曲线的对应较为困难。因此文献[15]中基于时频图像相减获得角多普勒信号的方法难以适用于该场景,需要利用信号处理手段对回波进行补偿,从而获得较为纯净的角多普勒信号。
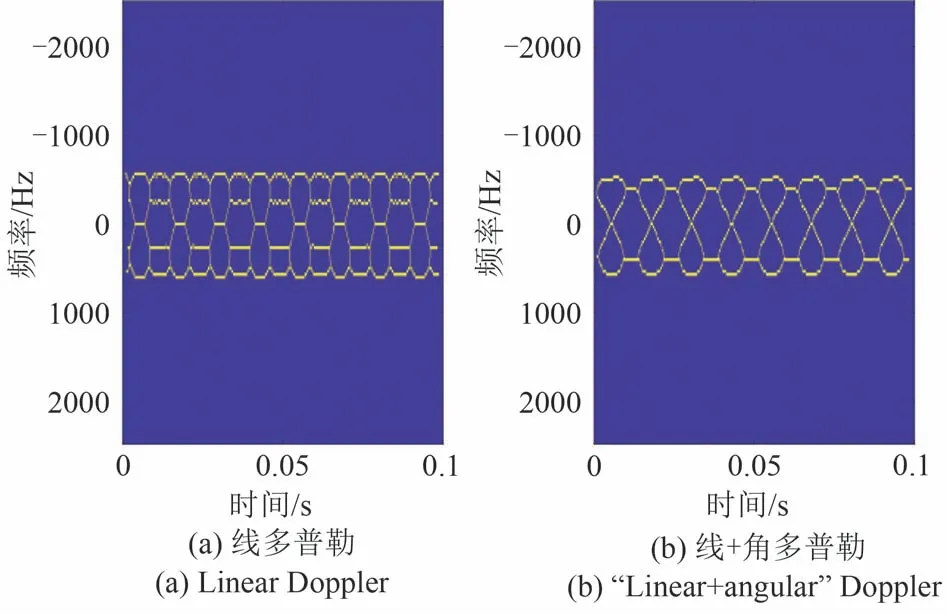
图6 骨架提取结果Fig.6 Skeleton extraction results
为克服图像域处理存在的问题,本文在信号域对回波进行处理,避免了复杂的曲线分离问题,角多普勒信号提取结果如图7所示。图7(a)为提取的角多普勒信号时频图,零频附近的时频曲线即为单个散射点的角多普勒。得益于补偿操作和滤波操作,时频图能量集中于所需的角多普勒上。图中存在类似于正弦曲线的干扰项,但该项能量较小,可通过设立全局阈值来消除该项。角多普勒时频图的骨架提取结果如图7(b)所示,由于角多普勒较小和时频分辨率的不足,骨架提取结果不够平滑,但仍能分辨其极值与极值点的位置。
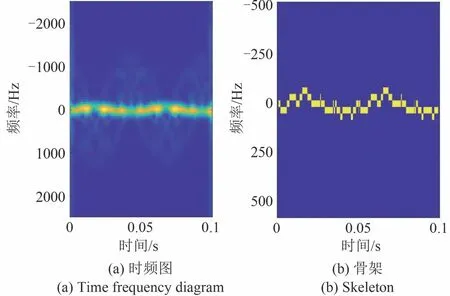
图7 角多普勒信号分离结果Fig.7 Angular Doppler signal separation results
在获得角多普勒时频图骨架后将其与对应的时频域坐标组成序列,获得如图8(a)所示的角多普勒频移。图8(a)中最大值为33.33 Hz、最大值点为0.0485 s,最小值为-66.67 Hz、最小值点为0.01643 s。图8(b)为理想的角多普勒频移曲线,角多普勒频移最小值为-70.5 Hz、最小值点为0.01663 s,最大值为22.55 Hz、最大值点为0.03587 s,曲线在最小值处变化剧烈,在最大值处变化缓慢。与图8(b)相比,(a)受限于时频分辨率,最小值和最大值均存在误差。由于最小值的变化较为剧烈,最小值点的估计精度较高;最大值处变化较为平缓,所以最大值点的估计误差较大。
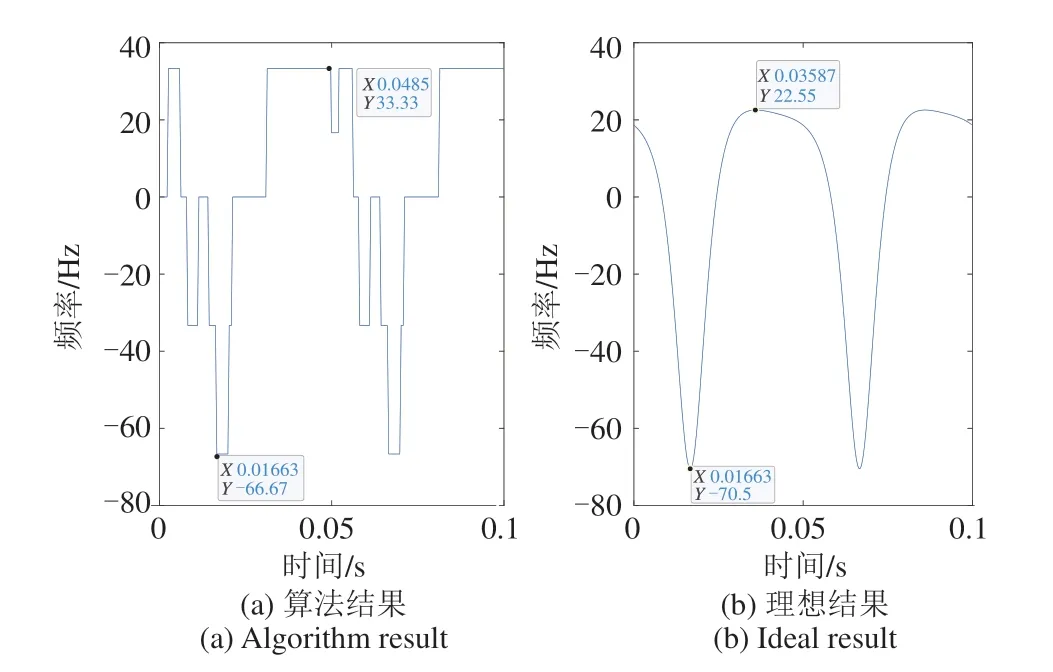
图8 角多普勒频移Fig.8 Angular Doppler shift
同时,为讨论算法在不同信噪比下的角多普勒提取能力,展示了信噪比为5 dB 时的角多普勒时频图和角多普勒频移曲线。如图9(a)所示,噪声的引入使曲线的能量分布发生一定变化,在边缘处出现毛刺,导致角多普勒曲线的极值估计误差较大。提取的角多普勒频移如图9(b)所示,曲线的最大值为66.67 Hz,远远大于实际值,最小值的估计误差较小。其原因在于单频信号受噪声影响较大,基于单频信号的角多普勒信号提取亦遭受较大影响。

图9 信噪比为5 dB时的角多普勒提取结果Fig.9 Extraction results of angular Doppler when SNR is 5 dB
图10展示了在不同信噪比下的估计误差。由于仅利用了单频涡旋电磁波,算法在5 dB 时已产生较大的估计误差,当信噪比小于5 dB时算法难以适用。同时由于算法利用角多普勒的极值的近似值,在信噪比较高的条件下仍存在一定的估计误差。为更直观的展示算法的微动参数提取能力,表3中给出了不同信噪比下算法的微动参数估计结果。旋转频率的估计精度较高,在各个信噪比下均实现了准确估计。在高信噪比下,对旋转中心坐标、倾斜角和旋转半径的估计精度较高。随着信噪比的降低,旋转中心坐标的估计误差增大,估计精度降低。倾斜角和旋转半径的估计精度高于旋转中心的估计精度。但在信噪比为5 dB时,平均估计误差达到了28.37%,算法难以准确的估计目标微动参数。其原因与上文分析的一致,基于单频信号的角多普勒信号提取受噪声影响较大,导致最终的微动参数估计结果误差较大。
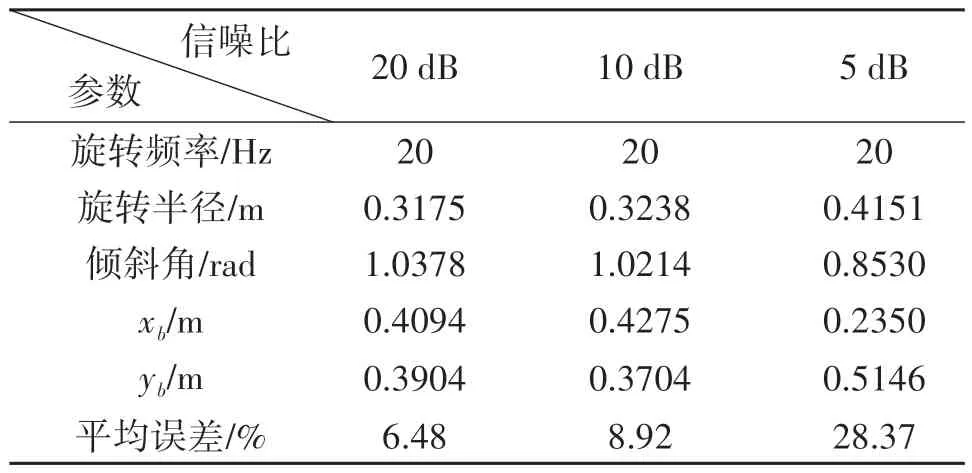
表3 微动参数估计结果Tab.3 The estimated results of micro-motion parameters
设定K=50,m2=500。在处理器为i7-1260P(2.10 GHz)的个人PC 机上,所提算法的运行时间为0.03 s,而在三维参数空间搜索所需的时间约为84.3 s,所提算法的运算速度显著提高。
6 结论
本文提出了一种无需时频曲线分离,可应用于角多普勒较小、旋转中心未知场景下的角多普勒信号分离方法。与现有方法相比避免了复杂的时频曲线分离与匹配问题,无需知道目标的旋转中心坐标。并利用微动参数关系式将微动参数估计中的四维空间的搜索变为一维向量搜索,降低了搜索维度。但由于单频信号的抗噪性能较低,因此该方法在较低信噪比条件下获得的估计结果存在一定误差,后续可进一步对本文所提方法进行拓展应用,研究基于线性调频信号等其他信号形式下的涡旋电磁波雷达微动参数提取方法。

