广义纳什均衡问题的精确指数—对数罚函数算法
杨 迪 何家文
1.南宁师范大学师园学院 广西南宁 530226;2.南宁学院通识教育学院 广西南宁 530200
纳什均衡问题是博弈论中一种非常重要的研究类型。广义纳什均衡问题(Generalized Nash Equilibrium Problem,GNEP)是纳什均衡问题的一种拓展形式,其中涉及的局中人决策影响其他局中人决策的情况,更能体现博弈问题中局中人之间普遍联系的实际情况。近年来,全球范围内经济的发展和市场竞争日趋激烈,已经不再是单个局中人选择策略就能达到最优策略的效果。单纯的纳什均衡问题已经不能满足实际需求,越来越多的学者通过研究广义纳什均衡博弈相关问题,以求能更好地推动社会和经济的发展。
本文在对指数精确罚函数和对数罚函数相关内容的基础上,利用这两个互为反函数的函数特征,提出一个指数—对数精确罚函数方法,用以求得广义纳什均衡(缩写为GNE),从而解决GNEP。
常用的约束最小值问题为:
minf(x)
s.t.gi(x)≤0.i=1,…,m,
(1)
其中f(x),gi(x):Rn→R是连续可微函数。
针对问题(1),文献[1]提出了一个联合指数罚函数法。这个方法在运行初始是不需要内点初始点,在选择初始点时有很大的选择空间,这样也能得到一个解,这是这个算法的优势,可惜效果跟内点法相似,不一定得到精确解。在文献[2]中,针对凸规划,利用精确指数乘子函数,也得到一个最优解。在前文基础型上,文献[3]则提出了一个精确的对数—指数乘子罚函数,得到一个较好的结果,这对提出新的罚函数算法给出了一个很好的示范。文献[4]利用指数型惩罚函数,对部分耦合约束进行惩罚,将广义纳什均衡问题的求解转化为求解一系列光滑的惩罚纳什均衡,进而得到想要的结果。文献[5-6]在研究串联机械臂系统轨迹规划问题、复杂的大规模极大极小值问题中,提出联合指数或对数罚函数法进行操作,给出相关算法的实际应用价值。这些学者在利用指数或对数罚函数来求解相关问题都做了有益的尝试,有利于我们进一步对广义纳什均衡问题进行探讨。
1 预备知识
假设博弈中有N个局中人,每一个局中人v∈{1,…,N}都有自己的策略集Xv,从自己的策略集Xv中选取一个策略xv。将每个局中人给出的策略形成一个组合,由此得到博弈中N个局中人的一个策略组合x=(x1,…,xN)。为突出我们所研究的某个局中人v的策略xv,记x=(xv,x-v),其中x-v=(x1,…,xv-1,xv+1,…,xN)表示除了局中人v之外,其他局中人所选择的策略形成的组合。我们以策略组合x为元素,构成局中人策略的集合,记为局中人策略集的笛卡尔积X,即x∈X:=X1×…×XN,并称X为局中人的策略组合集。令θv:Rn→R为博弈中每个局中人v的目标函数,为了更好地分析,假设θv(xv,x-v)对xv为凸。如果x*,v满足对v=1,…,N,(NEP)θv(x*,v,x*,-v)≤θv(xv,x*,-v),∀xv∈Xv。则向量x*=(x*,v,x*,-v)∈X称为一个纳什均衡(Nash Equilibrium,NE)。上述问题就是纳什均衡问题(Nash Equilibrium Problem,NEP)。
对现实当中的很多情况,博弈中的每个局中人在选择的策略的过程中,不仅要考虑自身情况,还要考虑其他局中人所选择的策略,由此来得到自身最大的收益或者付出最小的代价。为表示局中人在策略选择过程中策略之间的相关性,将每个局中人v的策略集表示为Xv(x-v):={xv|(xv,x-v)∈X},由此特别定义策略集组合集为Ω(x):=X1(x-1)×…×XN(x-N)。如果x*,v满足对v=1,…,N,(GNEP)θv(x*,v,x*.-v)≤θv(xv,x*,-v),∀xv∈Xv(x-v)。称向量x*∈Ω为一个广义纳什均衡(GNE),此问题就是本文重点要研究的广义纳什均衡问题(GNEP)。
在GNEP中,每一个局中人选择的策略与竞争对手所选择的策略是有相关性的。这更体现出在一些实际博弈中,局中人在进行策略选择时的相互影响。
针对GNEP,本文考虑了约束是不等式组的情况。在约束中,其中一部分是局中人v=1,…,N选择的策略依赖于其他局中人所选策略的约束,简称为依赖约束;另一种就是独立约束,即每个局中人的策略不依赖其他局中人的策略选择的约束。
针对局中人v,本文考虑的GNEP,只有依赖约束的最小值问题:
minxvθv(xv,x-v)
s.t.gv(xv,x-v)≤0,
(2)

Xv(x-v):={xv|gv(xv,x-v)≤0}
对所有v=1,…,N,针对原问题(2)需要一个全局假设:(1)目标函数θv:Rn→R是连续可微的,并且对所给xv为凸;(2)约束条件gv:Rn→R对所有i=1,…,m是连续可微的,并且对xv为凸。
2 精确指数—对数罚函数算法及其收敛性证明
针对广义纳什均衡问题(2),本文设计一个新的精确指数—对数罚函数:
由此得到一个精确指数—对数罚问题:
minxvMv(x,ρv)
(3)
经过分析计算,可得目标函数的梯度为:

如果出现这样的情况,就可以通过增大罚参数来强迫可行性,直至找到合适的解。
根据以上分析,给出精确指数—对数罚函数算法1。
算法1
步骤1 若xk是GNEP的解。停止。
步骤2 若xk不可行,且对任意v,若
(4)
则对所有v,使罚参数ρv加倍,令k←k+1,转步骤1。
下面证明原问题(2)与罚问题(3)是等价的。
定理1 如果算法1是有限步终止迭代,则原问题(2)的解与问题(3)的解等价。

反过来,要证问题(3)的解x*为(2)的解,我们只需证明x*为可行点。假设x*是不可行点,M(x,ρ*)在x*的邻域上连续可微,有:
0=∇xvM(x*,ρ*)
血管淋巴管瘤合并血管瘤属于特殊类型之一,就目前而言,临床报道较少,多以个案报道为主。影像学检查发现,以淋巴管和血管构成比不同而表不一为主,其中淋巴管患者的表现类似于淋巴瘤患者,血管瘤患者的表现类似于血管瘤。王小岩[10]在相关报道中发现,脾脏血管淋巴管瘤3例患者中,CT检查显示血管瘤样强化特征共计2例。瘤体内有出血表现时则清晰可见“液-液”平面现象。
故有:
算法1要求cv∈(0,1),那么对某些v和充分大的k,必定都会满足(4),根据算法1要求,更新罚参数,与题设条件产生矛盾。由此可得x*是可行点,而x*是可行点,就有问题(3)的解x*为(2)的解,本定理得证。
根据文献[3-4],我们新定义一些约束规格CQγ:
定义1 定义


定理2 假设由算法1产生的序列{xk}有界,对以下3个结论:(a)在xk的极限处,MFCQ成立,则CQ0条件成立;(b)在xk的极限处,CQ0条件成立,则罚参数只更新有限次。
对其中适当的子列,有下面的结论:
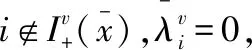
由于满足EMFCQ条件,当等式两边同时乘以dv时,就可以给出:
显然这是矛盾的。因此(a)成立。

3 数值结果
接下来的数值例子来说明算法1的可行性和有效性。
例1 考虑N=2的博弈:
其中局中人v=1决策变量为x1,局中人v=2的决策变量为x2,他们所受的共享约束是g(x1,x2)=x1+x2-1≤0。可得此博弈的最优解集为:
由此可以看出对α∈[1/2,1],本例是有无穷多个解(α,1-α)。根据文献[7],例1有唯一的变分均衡点(3/4,1/4)。
表1中p和pel分别表示经典罚函数算法和算法1,初始罚参数设置为ρ0=2。表1的数据表明,本文所提出的算法与经典罚函数相比,在迭代步数和时间上法不相上下,对任取初始点,都能得到有效数据。这说明提出的新算法是可行且稳定有效的。表1的数据也表明,在同样的误差内,算法1得到的解要比经典算法更为精确,这是新算法的优势所在。即在比较大的误差范围内(如ε=1.0e-3),算法1仍能保证最终迭代点与最优点的基本一致,比经典算法更加精确且迭代时间更短。

表1算法1和经典的罚函数算法得出的实验结果1
例2 考虑N=2的博弈:
局中人v=1的决策变量为x1,局中人v=2的决策变量为x2。他们有共同的约束g(x1,x2)=x1+x2-1≤0。分析可知例2唯一的最优点为x=(0,1),由此得到最优值-3。数值实验如下面的表2所示。
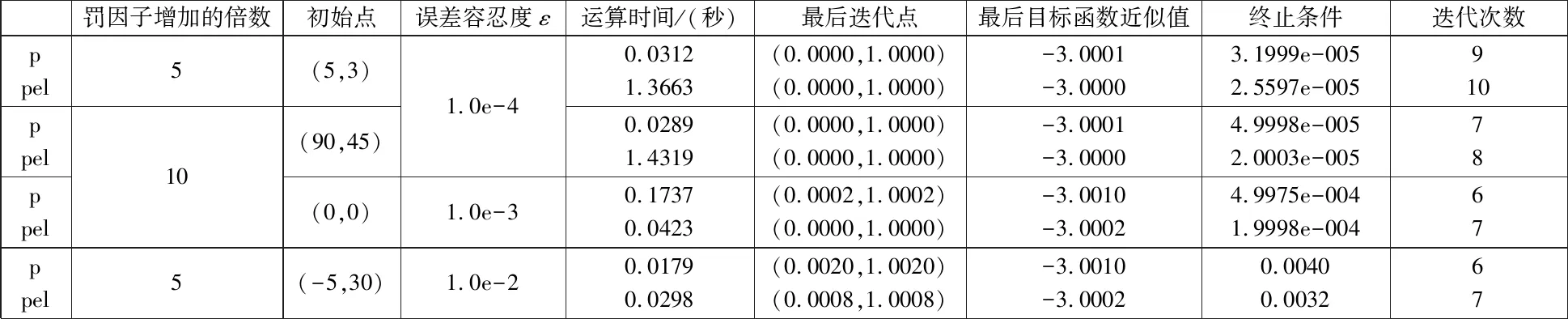
表2 算法1和经典的罚函数算法得出的实验结果1
从表2数据中可看出,在比较大的误差范围内,本文提出的新算法得到的解要比经典算法更为精确。通过综合表1与表2的数据,也可以看出在比较大的误差范围内,新算法得到的解要比经典算法更为精确,在多数情况下,迭代时间也要更短。这就意味着,在实际情况中,算法1满足在较低的要求下,仍然可以得到经典罚函数算法在高要求下才得到的解。这样就更能贴近现实生活的需求,显然是本文罚函数算法的优势所在。
结语
本文主要是利用精确罚函数方法来求解广义纳什均衡问题,针对不等式约束,提出了一个精确的指数—对数罚函数算法,并通过讨论算法的全局收敛性,给出数值结果来说明算法的有效性与可行性。
随着社会的发展,广义纳什均衡问题在现实世界中各个领域的应用越来越多,意味着我们需要解决具有各式各样要求的问题,并且这些问题内部联系越来越紧密。现有求解GNEP的罚函数算法都具有一定的局限性,与实际应用还存在一定的距离。往后,我们的研究方向仍有很多,比如,对更一般目标问题,像目标函数不为凸函数或约束函数不是凸函数的情况,还可提出对不是凸规划的算法等。

