基于半监督学习的端到端砂石细粒度检测方法

秦宋林,吕鹏,陈嘉浩,吴锐

(1.哈尔滨工业大学 计算学部, 黑龙江 哈尔滨 150001;2.中电建河南万山绿色建材有限公司, 河南 洛阳市 471900)

0 引言

骨料是构成混凝土最主要的材料,约占混凝土的60%～80%,因此,骨料质量的好坏直接决定了混凝土建筑强度和质量,关系着建筑物的安全。据报道,建成于1984年的北京内蒙古宾馆在1998年拆除装修中发现,1～11层有34根柱子出现纵向裂纹,裂缝长度由数十厘米至1.5 m 不等,裂缝宽度多为0.5～2 mm,大部分裂缝深度在20～40 mm,最深者达58 mm,超过混凝土保护层厚度,经检验证实是骨料质量问题造成的损坏。水电工程中非常重视料源母料的稳定性和骨料的综合性能,包括骨料的强度、坚固性和吸水率、骨料级配、粒形等,其中骨料的级配,即骨料中不同尺寸颗粒的粒度分布,是砂石骨料的重要质量参数,在骨料加工中需要对颗粒级配质量进行控制。根据中国砂石协会的数据,近5年中国砂石产量均维持在190亿t左右,2021年全国砂石产量为197亿t,其中70%以上为人工骨料。因此,研究一种快速的基于图像处理的砂石粒度检测方法,对砂石骨料破碎工艺的优化、对人工骨料产品质量控制具有重要的意义,属于人工骨料矿山智慧化生产的重要监测手段[1]。

基于图像处理的砂石粒度检测方法可以分为两种:基于传统图像的分割方法、基于神经网络的图像分割方法。传统视觉分割主要包括分水岭[2]、Canny算子[3]和Graph cut算法[4]等。Beucher等提出了分水岭算法,根据分水岭的构成来考虑图像的分割,分水岭算法在诸多分割任务中验证了操作的可行性。Canny开发出多级边缘检测算法Canny算子,创造了边缘检测计算理论并且应用于图像分割领域。Canny算子通过降噪、寻找图像中的亮度梯度、在图像中跟踪边缘等步骤完成图像的边缘检测,并且这种方法可以适用于不同的场合。Boykov等则将Graph cut用于分割任务当中。此类方法把图像分割看作像素标记问题,目标区域和背景区域标记为不同的值。通过最小化能量函数来得到目标区域和背景区域的边界即可得到分割结果。由于砂石图像对比度低,砂石互相遮挡,堆叠严重,分布密集,传统分割算法很难取得较好的效果。

基于深度神经网络的方法凭借其优异的特征提取和非线性映射能力,能够实现砂石图像更好的分割结果。通过将图像特征向量回归为一组输出向量来表示每个粒径范围的分布,可以对砂石粒度分布直接进行估计。LONG Jonathan 等提出了Fully Convolutional Networks(FCN)使用全卷积网络完成了像素级别的分割[5]。HE Kaiming 等提出了Mask-RCNN 网络结构同时解决了语义分割和目标检测问题,并且提出了ROI Align来解决传统的检测算法如Faster-RCNN 使用的ROI Pooling特征图不对齐的问题[6]。

不足的是,神经网络的训练严重依赖标注数据,实践中发现,对砂石图像进行正确的标注是极为耗时的。为此,本文提出了一种基于半监督学习的砂石细粒度检测方法。此方法可以简单描述为:第一阶段使用带标签的数据进行有监督的学习,获得一个预训练模型;第二阶段使用预训练模型对无标签数据打伪标签,然后使用伪标签数据和有标签数据进行联合训练。

1 算法描述

1.1 数据标注

砂石的分布信息无法从图像中直接获取,必须借助于统计图像中砂石的个数并且依靠每个砂石的粒径大小计算整体的粒度分布。对于一个砂石标注信息定义为(x1,y1,x2,y2),其中坐标系原点为图像左上方。标注如图1所示。

图1 砂石图像的粒径标注

设计离散型随机变量X,K个特定大小的粒径{t0,t1,…,tk}且满足t0≤t1≤…≤tk。标注的图像为一张图像所有砂石的粒径信息,因此需要完成粒径信息到粒度信息的转换。对于粒度分布P,有:

式中,P(tm≤X＜tn)为一张图像中粒径范围在[tm,tn)中砂石数目占总体砂石数目的比例;n为图像中砂石的总数目;A为图像中粒径的集合;另外随着数值K的增大,粒度分布P可以更好地对真实的粒度分布进行表达,设定K=6,即粒度分布曲线由6种指定的粒径进行划分。

1.2 模型训练

预训练过程如图2所示,采用反向传播方法训练模型,训练过程中采用KL[7]散度作为损失函数。骨架网络采用DenseNet-121[8]结构,如图3 所示。头部网络采用线性层。模型接受砂石图像输出粒度分布曲线,和真实分布曲线比较计算损失驱动模型进行学习。

图2 预训练过程

图3 DenseNet基本架构

1.3 砂石粒度检测伪标签生成

半监督算法面临的最主要问题是如何使用未标注数据来提升模型的性能。目前应用最广泛的半监督算法是基于伪标签的算法,即通过模型对未标注数据进行自动打标签。基于伪标签的半监督算法可以简单视作两个阶段的算法:第一阶段使用带标签的数据进行有监督的学习,获得一个预训练模型;第二阶段使用预训练模型对无标签数据打伪标签并且使用伪标签数据和有标签数据进行联合训练。训练流程如图4所示。

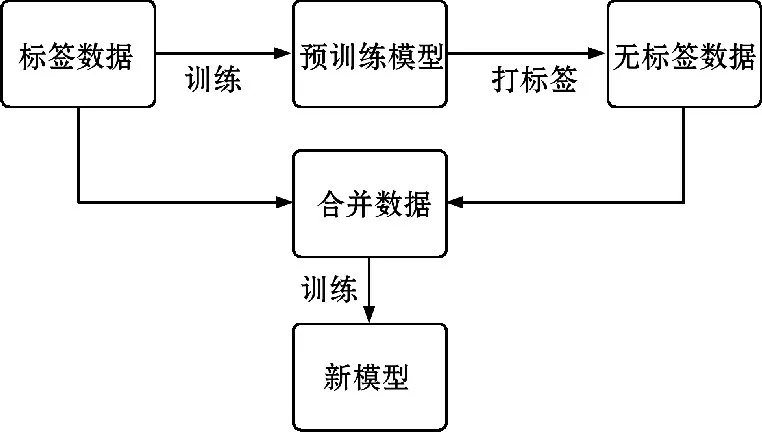
图4 基于伪标签的半监督训练

砂石粒度检测问题则不同于图像分类问题,需要的伪标签是砂石粒度的分布。伪标签需要从模型中获取。形式上对于粒度检测模型输出z,经过概率归一化后(softmax)y表达为图像砂石的粒度分布的预测值。表示为图像砂石粒度的真实分布,对于有标签数据是可以获取到的,对于无标签数据则无法获取。

最简单的伪标签策略为将z当作砂石粒度的真实分布,但这种方法无法对模型进行优化。此时,,当直接把模型输出当作伪标签处理则该样本的损失函数为零,损失函数为零则无法正常地产生梯度,进而无法对模型进行优化。

通过上述分析,输入和输出不可以完全一致,因此,需要对输出进行一定程度有意义的变换,使得输出和输入不再完全等价,进而产生分布的差异性,完成梯度反传和模型参数的更新。

具体地引入一个噪声分布ε～N(0,α),其中N代表高斯分布,α代表高斯分布的方差。对于输出y={y1,y2,y3,y4,y5,y6},其中zi表示为粒径范围[yi,yi+1)的砂石占全部砂石的比例。对每一种粒径范围,本文引入的伪标签为,即每一种粒径范围独立引入一个高斯噪声的扰动。引入高斯分布噪声可以在一定程度上反应工业相机无法拍摄的底层砂石分布对真实分布带来的影响。如图5所示,整体砂石粒度分布和表层砂石粒度分布存在一定程度上的差别,使用伪标签策略可以对这种差异性进行较好的建模。

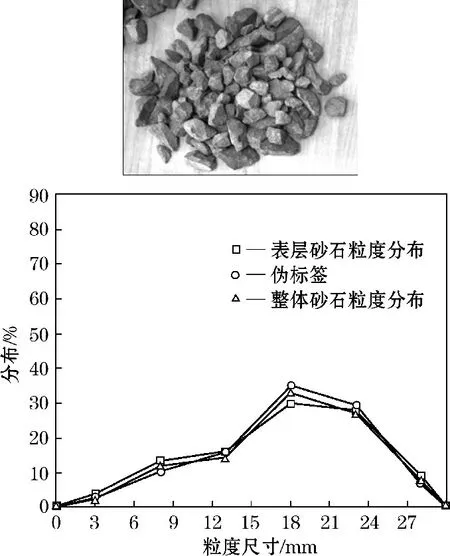
图5 底层砂石对整体分布带来的影响

引入噪声之后用来监督的真实分布发生改变,KL散度不再为零,模型可以通过无标签数据得到持续的优化。生成的伪标签如图6所示,模型预测结果和真实标签具有一定的差异性,生成的伪标签在一定程度上可以缓解这种差异性。

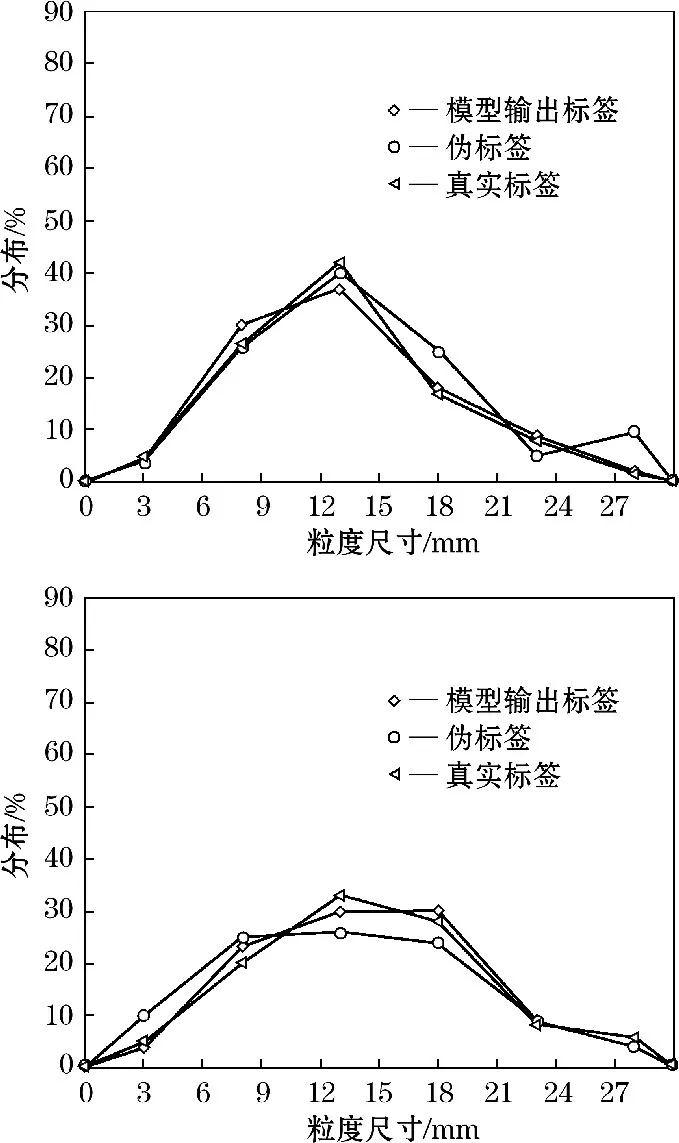
图6 伪标签生成示例

1.4 基于伪标签的半监督砂石粒度检测算法

损失函数如式(2)所示。

通过加入一个零均值的高斯分布N(0,α)的不确定性来完成伪标签的生成,对于超参数α,过高的超参数会导致模型难以收敛;但是较低的超参数无法提供有效的训练。因此,采用渐进式训练,即逐步增大超参数α的数值,让模型不断进行学习更新来达到收敛的目的。

式中,t代表训练期间的轮数,t0和t1代表预先设定的轮数。

公式(3)的含义代表在初始训练阶段,添加的噪声为零方差的高斯分布,这时候无标签不参与训练,模型并不会收到无标签数据的影响。在充分使用标签数据训练之后,逐渐增大高斯分布的方差,模型开始对不确定性进行建模。对于超参数进行线性的稳定增长策略,这样可以避免模型不确定性过高带来的难以收敛问题。设置最大方差为0.05,即最大的不确定性,在训练后期超参数α不会再进行增高。

提出的适用于砂石粒度检测的半监督算法有效果的原因除了之前分析的伪标签可以建模到砂石图像下面掩盖的砂石的分布情况,再者就是对模型提供了一种正则化的手段,通过对伪标签加入一定程度的不确定性使得样本能够持续不断地提供损失让模型进行学习。

2 结果分析

为了能更好地进行比较,采用了两种评价指标分别是均方误差和正确率。

均方误差计算方法如式(4)所示:

式中,Ek为6种指定粒度中第k个粒度的误差,N为测试集的大小,zi为预测粒度分布,为真实的粒度分布。

上述指标是针对6个粒度范围设计的各自评价指标,对于整体粒度分布的均方误差如式(5)所示所有粒度误差的平均值。

均方误差指标能够较好地反应模型对整体数据集预测结果和真实值之间的误差,但是无法较好地衡量单个样本的粒度检测结果。因此提出正确率指标衡量分割结果:

不同算法的均方误差对比结果见表1,正确率比较见表2。

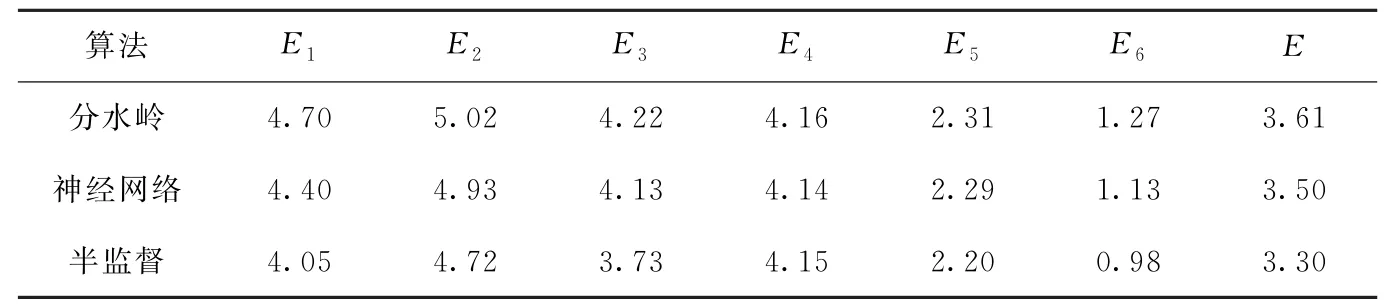
表1 不同算法均方误差对比结果 %

表2 不同算法正确率对比结果 %

由表1可知,相对于基于神经网络的方法,提出的半监督算法能有效降低各个粒径的均方误差。

在正确率评价指标上可以看到,半监督算法相比于神经网络而言有不同程度的提高。可越宽松的边界对于算法性能的提升越小,边界效应的存在导致提升困难。

3 结论

基于神经网络的方法需要大规模数据进行驱动训练,对于数据集的标注耗费大量的时间。因此,使用半监督算法来对粒度检测任务进行优化。半监督算法往往应用在图像分类任务中,在粒度检测任务中属于空白,将现有半监督算法扩展至粒度检测中。提出了一种基于伪标签的半监督算法。并且最终的试验结果证明了提出方法的有效性。该方法可以完成端到端砂石细粒度检测,并且展现了非常好的效果。在伪标签的半监督算法中,由于伪标签的随机性的存在将会带来难以收敛的问题,在未来工作中将会使用基于学生老师的半监督算法解决这个问题。