柱状透镜阵列对物体隐形现象的探究
苏诣博,王 拴,曹 峰,陈书湄,邓柏昌
(哈尔滨工业大学(深圳) a.电子与信息工程学院;b.实验与创新实践教育中心;c.理学院,广东 深圳 518055)
柱状透镜阵列对物体的隐形现象是2022年中国大学生物理学术竞赛的题目之一,柱状透镜阵列(Lenticular lenses)会对光线传播产生扭曲从而使“物体隐形”. 柱状透镜阵列被广泛应用于印刷显示、显示屏等领域,透镜阵列与交错的打印图像共同作用可以实现3D、动画、翻转、变形、缩放或各种组合等视觉效果[1-7]. 目前揭示柱状透镜阵列对物体隐形现象的物理原理和隐形效果[8-9]衡量方法的相关研究工作较少. 本研究工作综合运用几何光学和光度学理论,较好地解释了利用柱状透镜阵列实现对物体隐形现象的物理机制,通过类比高斯光束的能量分布[10],借鉴瑞利判据思想[11],提出了临界隐形物距的概念,可作为衡量柱状透镜阵列隐形效果的关键参量,对设计制造具备较好光学隐形特性的柱状透镜阵列具有参考意义. 同时,本文也通过光学物理场仿真和实验探究了透镜单元间距、曲率半径、折射率以及物体几何形状等因素对隐形现象的影响. 本研究所涉及的实验对器材及场地要求较少,可在实验室或居家完成,可作为大学物理实验教学创新设计型项目,也可作为高校物理及光电信息相关专业课程内容的拓展.
1 理论分析与物理场仿真
1.1 柱状透镜阵列单元的放大率
柱状透镜阵列是一系列圆柱状微小透镜排列组成的阵列,柱状透镜阵列单元为单个的柱状透镜,其厚度等于其焦距f,只有一面有曲率,另一面为平面,且有曲率的面只在1个维度上有曲率,这与普通凸透镜(球状面)在各个方向都有曲率不同.以O为原点建立空间笛卡尔坐标系,如图1(a)所示,由于柱状透镜阵列只在平行于x轴的方向上有曲率,故只讨论物体沿x轴方向的宽度d,如图1(b)所示.

(a)柱状透镜阵列示意图
由于柱状透镜阵列成像的大部分光强能量处于物体中心轴线位置,对于隐形现象的观测也主要位于中心轴线处,因此采用了傍轴条件对理论模型进行简化.在傍轴光线条件[12]下,物体第1次成像(以O1为顶点)为平面折射成像[见图1(c)],由单球面折射的物像公式可得
(1)
其中,n0为柱状透镜阵列单元的折射率,空气折射率近似等于1,p1为物体第1次成像的物距,p1′为第1次成像的像距,r为曲率半径.对于平面有r→∞,易得第1次成像的放大率为k1=1,即平面不对物体产生放缩.第2次成像(以O2为顶点)为单凹球面折射成像,由单球面折射的物像公式可得
(2)
其中,p2和为p2′分别是第2次成像的物距和像距.由图1(c)可知,p2=p1′+f=n0p1+f,代入式(2)得第2次成像的像距为
(3)
进而得到第2次成像的放大率为
(4)
故柱状透镜单元对物体2次成像的总放大率为
(5)
由几何光学的符号法则和透镜的几何尺寸(一般r≪p1)可知:k<0,|k|≪1.故整个成像系统始终成倒立、缩小的实像.
1.2 光度学理论引进及光学仿真
由于物体的不同物点相距很近,单个物点发出的光强近似服从余弦分布[13],且柱状透镜阵列存在像差,即第n个透镜单元与相邻2个透镜单元(第n-1和第n+1个透镜单元)成像时的光强会发生重叠从而导致图像串扰,如图2(a)所示.串扰效应解释了柱状透镜阵列对物体成像边缘会有模糊延伸现象[14],图2(b)为串扰成像示意图,其中左侧为成像物体,右侧为经过柱状透镜阵列后的成像.由于柱状透镜阵列的串扰效应,在讨论其成像时必须引入光度学的概念来界定其隐形的临界条件.
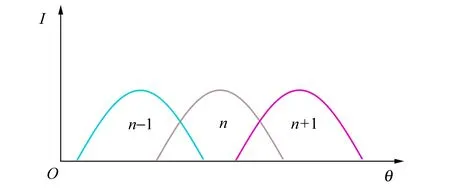
(a)光强重叠导致图像串扰示意图
1.2.1 物体空间光强分布
实际物体一般为不发光物体,其表面一般为漫反射表面,光强I具有近似余弦辐射的特性[图3(a)].物体可近似看作余弦辐射体,其在空间内的光亮度为定值L,设物体表面的光照度为M,则M与L有如下关系:
(6)
其中,θ和φ是立体角的2个辅助平面角.由式(6)可推导得到物体表面的光照度M为定值.
1.2.2 隐形条件的探究
首先,房地产开发企业的经营产品具有着非标准性特点。具体一些解释,由于各个楼盘的所处地理位置与开发核心都有所不同,因此导致楼盘的整体风格也有着很大差异。房地产开发项目前需要展开综合考量,其中包括开发区域的经济发展水平、人文环境、居住需求等,有针对性的完成设计方案。
根据瑞利判据[15],考虑到可见光波长平均值(λ≈550 nm)和瞳孔直径(φ≈3 mm),人眼在明视距离(u≈25 cm)处能分辨的最佳特征[16]是d′=1.22usinθ=1.22uλ/φ≈0.056 mm.
借鉴瑞利判据思想[图3(b)],柱状透镜阵列对物点成像,当物距较小时,放大率的绝对值较大,成像宽度较大,成像会有重合;物距增大,像缩小,由重合变为不重合,即像分离,如图3(c)所示.其中,Δx是相邻2个透镜单元成像的距离,由图3(c)可知
Δx=(k+1)l,
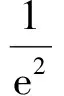
考虑人眼对极小物体的分辨情况,柱状透镜阵列使物体隐形需同时满足以下2个条件:
2)上述光斑的宽度小于人眼的分辨率(d′=0.056 mm) .
写出上述条件的表达式为
kd>d′,kD<(k+1)l,
(7)
(8)
式(8)即为物体的临界隐形物距表达式,即当物体物距p1大于临界隐形物距p0时,可以观察到物体的隐形现象.柱状透镜阵列物体的隐形效果会随物距渐变,因此可以用临界隐形物距p0的大小来衡量柱状透镜阵列对物体的隐形效果.p0越大,说明需要物体距离透镜更远才能隐形,物体的隐形效果相对更差;反之亦然.
1.2.3 光学仿真
使用VirtualLab Funsion高速物理光学软件进行光学物理场仿真并测量光斑宽度D值. 选择非序列模式,设置被观测物体为平面矩形物体光源,并绘制三维柱状透镜阵列实体模型,进行光线追迹并使用探测器进行光照度探测,得到光照度分布. 仿真的被观测物体的光照度呈均匀分布,如图4(a)~(b)所示. 经柱状透镜阵列后的透射光光照度分布如图4(c)~(d)所示,其中x轴光照度从中心向两侧递减,且其形状与高斯光束类似.根据这一特点,可类比高斯光束的能量分布特点研究透射光光照度的分布情况.根据以上光学仿真,可以得到经过柱状透镜阵列后透射光光照度分布图4(d),其中Mmax为被观测物体宽度d位置处的光照度(近似等于最大光照度),光照度降低至Mmax/e2时,可以求得光斑宽度D(该光斑范围内包含约86.5%的光能).结合式(8)可求出该实验条件下柱状透镜阵列的临界隐形物距p0.改变柱状透镜阵列成像的条件(如曲率半径r、透镜间距l、被观测物体宽度d等)进行光学仿真,即可获得其他参量条件下的临界隐形物距p0.
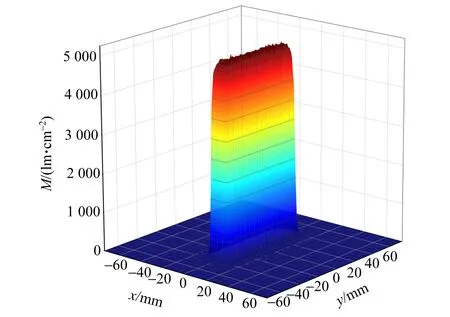
(a)被观测物体光照度空间分布
2 实验验证
2.1 实验器材
采用不同参量的柱状透镜阵列(材质为PET)、不同颜色的卡纸、白板、刻度尺、光具座、高清摄像机等器材进行实验,实验装置示意图如图5所示.
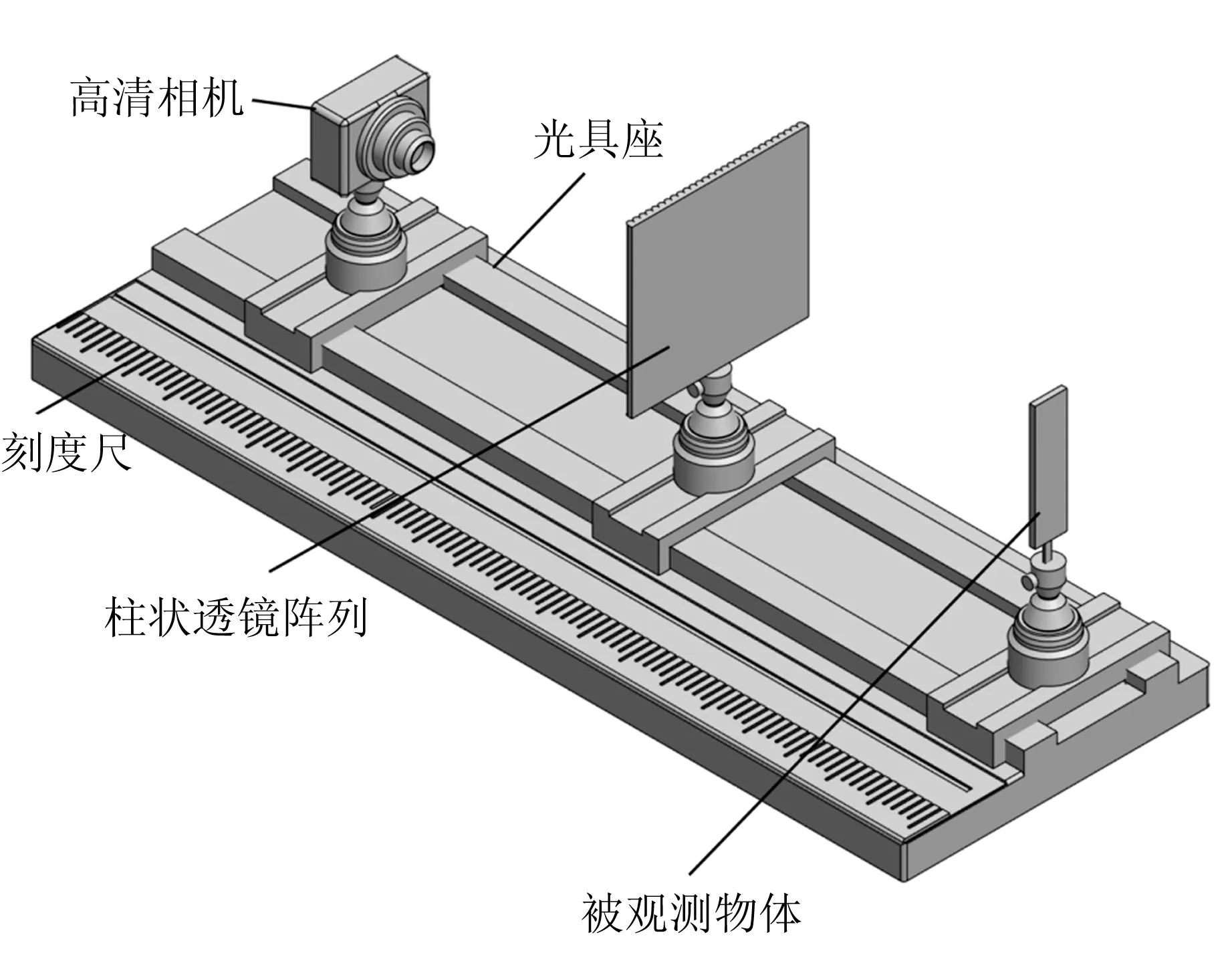
图5 实验装置示意图
利用式(8)计算柱状透镜阵列的临界隐形物距理论值p0,取不同的物距观察隐形现象,并用摄像机记录物体的隐形情况,对比不同情况下的隐形效果,实验条件如表1~2所示.
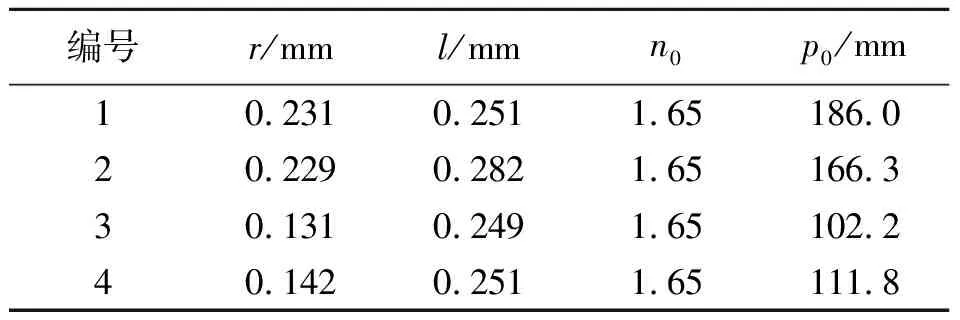
表1 柱状透镜阵列参量及临界隐形物距理论计算数据 (物体宽度d=20.00 mm)

表2 不同物体宽度对应的临界隐形物距理论计算数据 (透镜1)
在实验中需要注意:
1)柱状透镜阵列只在1个方向有曲率,故只在1个维度(平行于柱状透镜阵列排列方向)上对物体有隐形作用;
2)被观测物体需保证在垂直于柱状透镜阵列排列方向上的长度不能过大,否则不能实现较为理想的隐形效果.
2.2 实验结果与讨论
2.2.1 物距对成像的影响
通过柱状透镜阵列观测物体隐形情况如图6所示,其中图6(a)和图6(b)的实验过程为:保持柱状透镜阵列参量(曲率半径r、透镜间距l)、被观测物体宽度d不变,只改变物距p1,探究p1对隐形的影响.可以发现随着p1不断增大,物体成像逐渐模糊,隐形效果逐渐增强;当p1增加到临界隐形物距p0时,开始出现隐形现象,继续增大物距时可实现完全隐形效果.同时也可以发现,在相同物距p1和相同物体宽度d的实验条件下,柱状透镜阵列的临界隐形物距越小,隐形效果越好,如图6(c)所示.

p1=145.0 mm p1=p0=186.0 mm p1=225.0 mm(a)物距对成像的影响(透镜1,r=0.231 mm,l=0.251 mm,d=20.00mm)
2.2.2 柱状透镜阵列属性对成像的影响
由理论和仿真可知,柱状透镜阵列单元间距l和曲率半径r对临界隐形物距p0具有重要影响.当柱状透镜阵列的折射率相同时,对于同一宽度d的物体成像,分别计算不同l和r值下的p0,增大l或者减小r,均可使p0减小,即柱状透镜阵列的隐形效果越好.图6(c)的实验过程为:保持柱状透镜阵列部分参量(透镜间距l)、物距p1和被观测物体的宽度d不变,只改变柱状透镜阵列曲率半径r,探究柱状透镜阵列曲率半径r对隐形效果的影响.在实验中发现,在相同物距条件下,r=0.142 mm的柱状透镜阵列隐形效果优于r=0.231 mm的柱状透镜阵列,即曲率半径越小,隐形效果越好;透镜间距l较大的柱状透镜阵列的隐形效果更优[对比图6(a)和图6(b)].
2.2.3 物体几何形状对成像的影响
图6(d)的实验过程为:保持柱状透镜阵列参量(曲率半径r、透镜间距l)、物体物距p1不变,只改变被观测物体的宽度d,探究了被观测物体宽度d对隐形的影响.实验现象表明:物体宽度d越大,实验观测图像与被观测物体原图像的相似程度越高,隐形效果越差;物体宽度d越小,图像实验观测图像与被观测物体原图像的相似程度越低,隐形效果越好.
2.3 临界隐形物距的适用性
本研究适用于傍轴光线条件,可以较好地解释柱状透镜阵列属性、物体几何形状对柱状透镜阵列隐形现象的影响及其物理机制,同时证明利用临界隐形物距评估柱状透镜阵列的隐形特性具有较强的可行性和准确性.对于其他构型的透镜阵列也具有推广性,可通过几何光学和光度学理论求得放大率表达式,并依据本文方法求得相应的临界隐形物距,从而确定其隐形特性.
非傍轴光线条件下,当柱状透镜阵列透镜单元曲率半径较大、焦距较大、空间频率较小时,物体成像的不均匀重影现象以及柱状透镜阵列的广义衍射现象(傅里叶光学)[17]仍值得进一步探究.
3 结束语
以几何光学为基础,引进光度学理论,通过类比高斯光束的能量分布,借鉴瑞利判据的思想,提出了临界隐形物距的概念,借助该参量可以很好地衡量柱状透镜阵列隐形的效果,并利用光学物理场仿真模拟得到了柱状透镜阵列透射光的光照度分布,对柱状透镜阵列实现物体隐形现象的影响因素进行了探究.本研究不仅丰富了光学隐形技术理论,同时对于设计和评估具备较好光学隐形特性的柱状透镜阵列具有参考意义.

