弗兰克-赫兹实验集电极电流微分测量分析
李潮锐
(中山大学 物理学院,广东 广州,510275)
弗兰克-赫兹(Frank-Hertz,F-H)实验利用热电子在外电场加速过程中与原子交换能量,通过测量集电极电流变化推断原子激发电位. 常规方法可观测到的实验现象普遍包括:
1)随集电极电位VP增大,集电极电流IP的起始第二栅极电压VG2升高;
2)随VP增大,IP-VG2曲线整体下移;
3)随VP增大,IP-VG2曲线中的IP谷电位或峰电位向VG2高电压端移动;
4)即使VP高于原子激发电位,仍可清晰地观测到IP-VG2的变化规律;
5)在VP恒定的条件下,IP-VG2曲线随VG2增大呈现类周期振荡上扬;
6)原子激发电位随VG2升高而逐渐增大(激发电位递增).
文献[1]指出:不管在发生能量交换之前还是之后,管中热电子电流都具有能量分布规律.常规实验方法中,IP来自所有能量高于VP的热电子的贡献,或者说,IP是对所有可到达集电极热电子(流)的累加(积分)测量结果.本文采用集电极电流微分测量方法,通过集电极微分电流iP(V)的能量(电位)分布讨论分析F-H实验的普遍现象.根据iP(V)能量分布峰形特点及变化规律,从IP微分测量角度理解实验测得的原子激发电位递增现象的物理本质.
1 实验技术方法
实验主体装置是复旦天欣弗兰克-赫兹实验仪(I型),包括灯丝电源、第一栅极电源、第二栅极电源、集电极电源和集电极电流放大测量等功能模块.常规接法是以集电极P为接地端,这有利于集电极电流放大测量电路设计,实验所用的运算放大器由+12 V和-12 V双电源供电. 关于常规方法的F-H实验参量优化及其结果评估参见文献[2].
使用实验仪内部灯丝电源VF=1.70 V,以使实验中最大集电极电流IPmax不超量程;不施加第一栅极电位,即VG1=0 V. 改用艾德克斯(iTech)IT6874B直流电源和普源(Rigol)DP831A直流电源分别提供第二栅极电压VG2和集电极电位VP,外部电源也将VG2和VP分别扩大至0~100 V和0~30 V(甚至更高)范围;二者均采用约0.20 V的步进实施测量. 用吉时利(Keithley)DMM7510多用表测量集电极电流IP(实际测量的是由运算放大器输出电压来表征IP),2台普源(Rigol)DM3068多用表则分别用于测量VG2和VP.泰克(Tektronix)AFG3252信号源为集电极提供频率为27.8 Hz且其峰-峰值为0.200 V的交流调制电压,并与集电极直流电源输出(串联)叠加,由中大科仪OE1022I数字锁相放大器测量IP交流分量(实际测量的是运算放大器输出电压交流分量);以AFG3252信号源TTL同步输出为OE1022I锁相放大器外参考信号. 通过RS232,USB和GPIB接口对实验系统实施计算机测控操作和数据采集分析.
实验过程可能会遇到2个问题:
1)在VP接近或高于原子激发电位,即IP较微弱时,IP出现负值.特别是灯丝电流较小情况,IP负值更为明显.
2)改变VP对VG2存在的弱影响.
图1所示为实验测量电路等效示意图.无论是从阴极发射出来随之进入加速区,还是从加速区经过第二栅极进入减速区,热电子都具有初速度(初动能或初能量),这等效于有电源驱动.因此,在加速区和减速区的回路中,除了电路中的实体电源外,还应该考虑附加等效电源的作用.

图1 F-H实验等效电路示意图
图1中,EG2和EP分别为第二栅极和集电极可调等效电源,VG2和VP则分别为第二栅极和集电极所施加的(可测)电位,RG2和RP分别表示F-H管加速区和减速区的等效电阻,R为第二栅极等效电阻,IG和IP分别为加速区和减速区回路电流.根据基尔霍夫电压定律可得
EG2=VG2+VR,
(1)
-EP=VP-VR,
(2)
其中,
VG2=RG2IG,
(3)
VP=RPIP,
(4)
VR=(IG-IP)R.
(5)
由式(2)、式(4)和式(5)可得
(6)
由式(5)和式(6)可知,当EP增大时,IP减小,VR增大.可以认为,此时绝大多数热电子已穿过第二栅极进入减速区,或者栅极等效电阻比RG2和RP都小得多.因此,随EP增大,将可能出现IP为负值的情况.
由式(1)~(6)可知,在任一设定EG2的情形下,当EP增大时,IP减小,VR随之变化,从而使VG2发生改变.实验事实也表明:VG2随EP发生微弱变化.因此,在测量iP(V)-V的能量(电压)分布过程中,每次改变EP都需要对EG2输出进行及时修正,以确保VG2恒定.
上述分析表明:IP负值和VP与VG2相关联.首先,确认(调节)IP测量电路的静态工作零点.为解决集电极电流微分测量中VP变化对VG2的弱影响,每当改变VP时,同步调节IT6874B直流电源输出以使VG2恒压.在VG2<70 V时,恒压精度优于10 mV,而高电位端恒压精度则优于16 mV,由此保证实验测量的准确性.
2 实验结果与分析
2.1 常规方法的实验结果
图2所示为IP-VG2的实验结果.由图2可见,IP随VG2的增加呈现类周期振荡上扬.不同VP下的IP-VG2曲线清晰地显示了上述6种普遍实验现象.表1记录了不同VP情形下IP峰处的VG2,可以看出:IP峰处对应的VG2随VP的变化而变化,经计算还可以发现由两相邻峰的VG2差值所得的原子激发电位也随着VG2的增加而逐渐增大(激发电位递增).
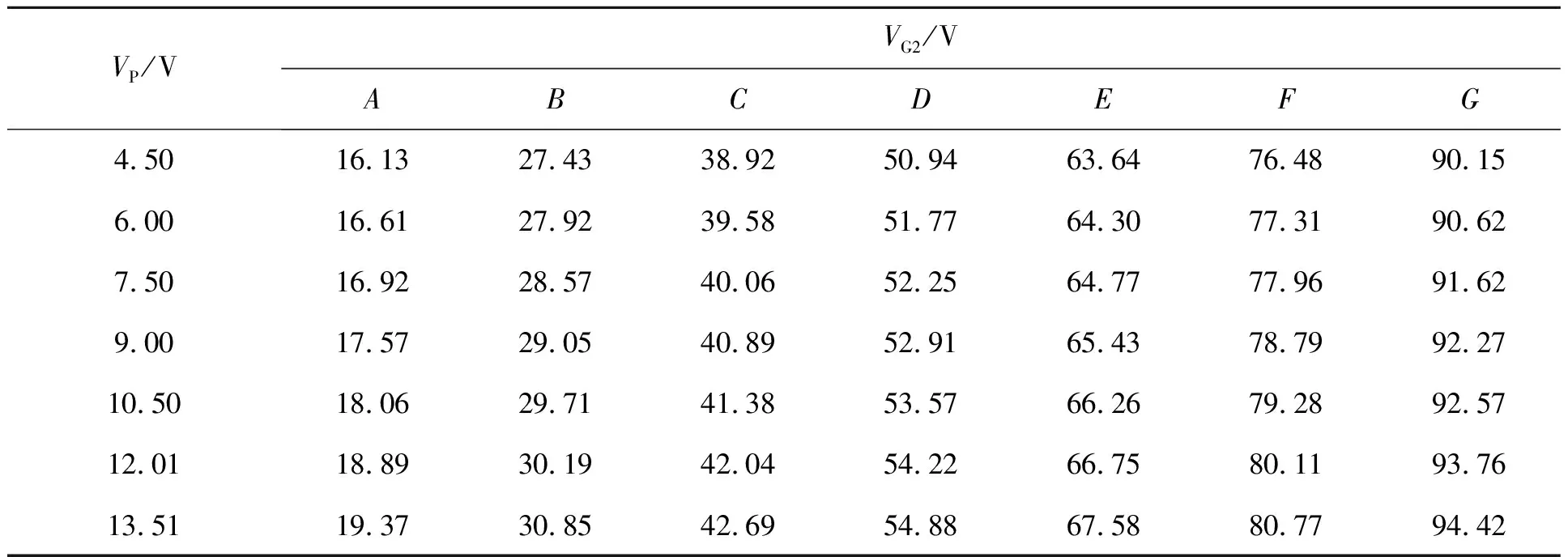
表1 不同VP情形IP峰处的VG2

图2 不同VP情形下IP-VG2实验结果
2.2 集电极电流IP微分测量原理
关于F-H实验的普遍现象,已有文献进行了广泛观测和描述[3-8]. 在确定的VG2条件下,栅极热电子将具有不同能量,且呈现粒子数的能量分布规律. 若忽略由第二栅极到集电极之间原子对热电子运动的影响,那么图2中的IP表示处于第二栅极所有电位V高于VP的热电子的集体贡献.在确定的VG2和VP条件下,假设电位为V的热电子对集电极电流的贡献为iP(V),那么IP可表示为(等效于并联电路)
(7)
将式(7)改写成离散化积分形式
(8)
如果不考虑减速区中原子的影响,那么到达集电极的热电子与处于第二栅极的热电子的能量分布规律相同.因而,在确定的VP处,施加微小调制ΔVP,测量对应的IP变化量ΔIP,即实施V=VP时的IP微分测量,且由此得到具有电位VP的热电子的贡献iP(VP).一系列不同的VP所构成的iP(VP)-VP关系可以表示到达第二栅极时热电子电流的电位分布规律iP(V)-V.
当VP=0时,增大VG2直至可以观测到IP和iP(V),以此为实验起点.具体步骤为:
1)同步采集VG2,IP,VP和iP(VP);
2)步进增大VP,并重复步骤1),直至VP达到最大值,完成在VG2不变条件下iP(VP)-VP的测量;
3)将VP调回最小值,并重复步骤1);
4)适量增大VG2,按步骤1)~3)重复完成实验测量,可得到一系列不同VG2条件下的iP(V)-V结果.
图3显示了VG2=17.68 V,IP与iP(VP)随VP的变化关系.在任一确定的VP处,常规方法的集电极电流IP(蓝色线上的数据点)为V≥VP条件下所有iP(VP)(红色线自VP起在高能端的所有iP数据点)的累加结果,由式(7)表示;或者说,是由iP(VP)-V能量分布(红色线)在V≥VP范围内与iP(VP)=0基线所围面积,由式(8)描述.注意:IP与iP(VP)累加或积分结果可能相差(积分)常量.

图3 IP与iP(VP)随VP的变化
由图3可知,对于任一确定的VP,IP为电位V≥VP情形下所有(可能)iP(V)的累加(积分).若对每个确定(恒定)的VG2逐一完成所有V≥VP情形下iP(V)的累加也可得到图2中IP-VG2的结果.或者,在V≥VP情形下,逐一测量每个确定VP的iP(V)-VG2数据,进而将所有数据在不变的情形下叠加,也可得到图2中VP条件下IP-VG2的结果.
综上所述,在VG2确定的情况下,IP来自V≥VP情形下所有(可能)iP(V)的集体贡献,而每个iP(V)在IP中具有不同占比.图4显示了不同VP情况下iP(V)-VG2的实验结果.曲线均呈现出与IP-VG2相似的类周期振荡趋势,还直观地显示了不同VP下iP(V)-VG2在IP-VG2中的占比差异,同时不同VP之间的相对占比也随VG2发生变化.由此可知,当VP确定时,iP(V)-VG2在IP-VG2中的占比随VG2的变化而变化.值得一提的是,即使在VP=13.51 V的情形下,依然可以清晰地观测到iP(V)随VG2的类周期振荡趋势.
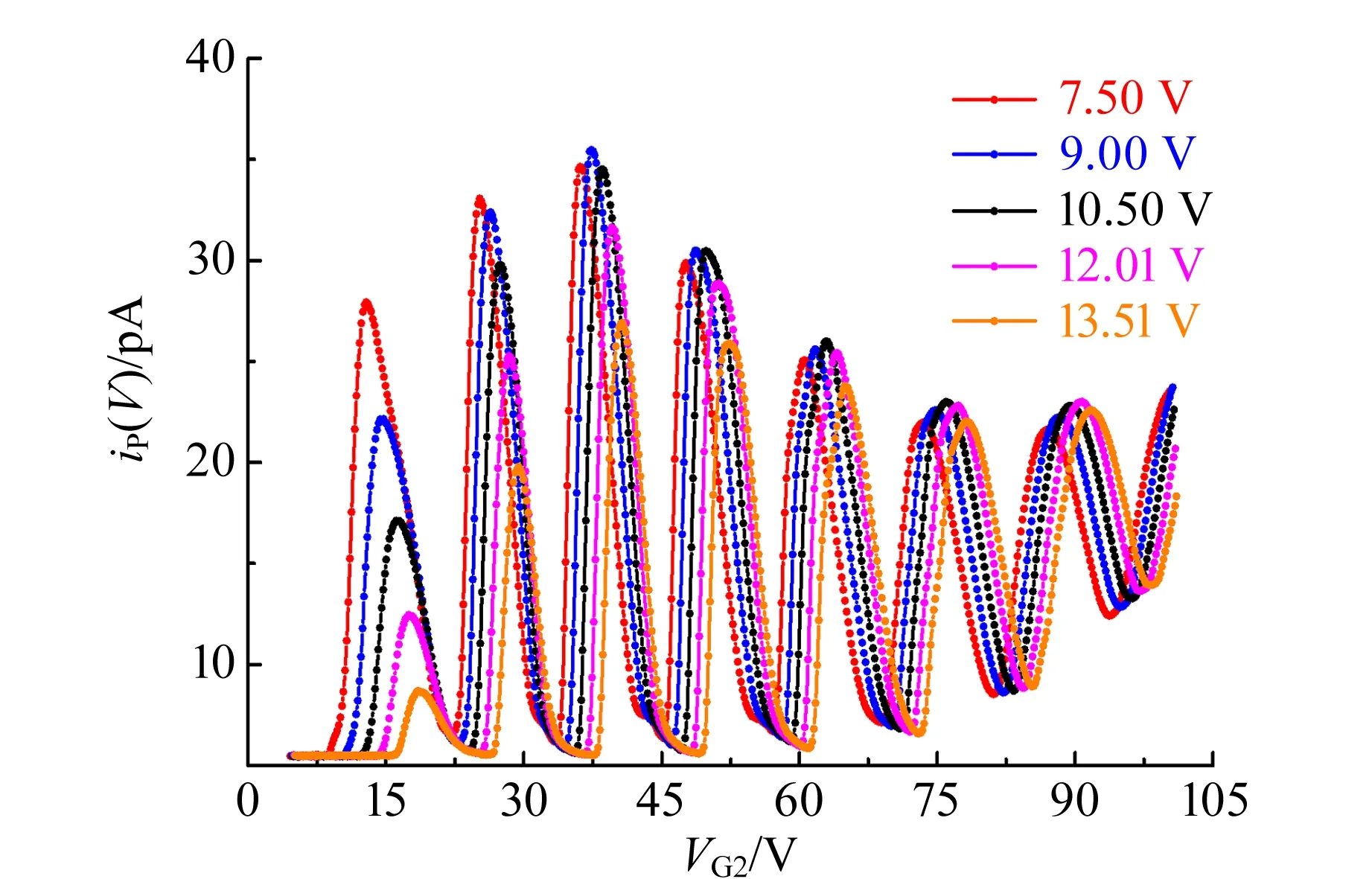
图4 不同VP情形下iP(V)随VG2的变化情况
2.3 集电极微分电流iP电位分布
从阴极发射出来的热电子,在逸出阴极表面时遵从狄拉克-费米分布,这也正是真空管情形测量金属电极电子逸出功(函数)的物理依据.F-H管不是真空管,管里充有原子气体.热电子自阴极发射出来后,在VG2的加速作用下,伴随着向集电极方向热运动的同时,还与管中原子不断发生碰撞(甚至发生原子激发交换能量).此过程中,在确定的VG2作用下,管中热电子都必将达到具有能量分布的动态平衡.
图5显示了不同VG2情形下,微分电流iP(V)随VP的分布情况.事实上,在VG2略小于3.50 V时已有少量热电子到达第二栅极,且当VP=0时可观测到微弱的IP和iP(V).逐步增大VG2,当VG2≥5.71 V,iP(V)能量峰形分布逐渐清晰.同时,随着VG2的增大,热电子可获得更多(平均)能量,从而使iP(V)峰位向VP高能端移动,且iP(V)峰宽同步增大.假设单位时间从阴极发射出来的热电子数量基本稳定,那么相应的能量峰高必将下降,能量分布整体向下压缩.图5所示实验结果与上述热电子能量峰形分布随VG2变化的分析结果一致.可以得出:iP(V)呈现的峰形能量分布并非VP的δ函数,这增加了准确分析IP-VG2物理过程的难度.文献[9]也通过实验观测了抵达集电极热电子的能量分布规律.
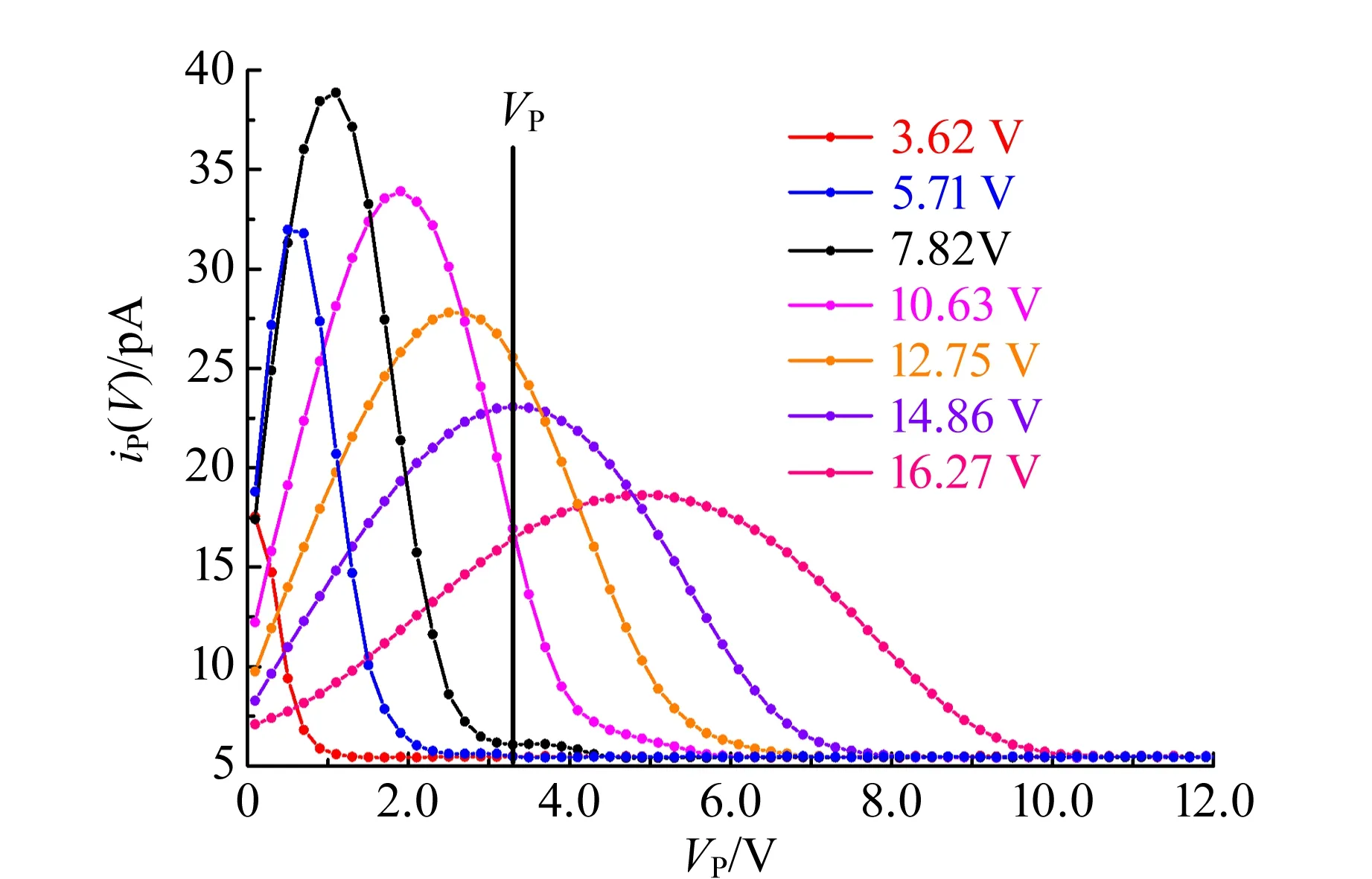
图5 不同VG2情形下iP(V)随VP的分布
2.4 集电极电流随集电极电位的变化分析
VP也被称为阈值电位(能量),对于任意VP,只有V≥VP时,热电子才可被测量.图5中,当VG2≤7.82 V时,无法观测到IP起始信号.随着VP的增大或减小,IP起始信号对应的VG2也相应地上升或下降.图5实验结果解释了普遍现象1):随VP增大,IP的起始第二栅极电压VG2升高.
对任一恒定的VG2,在VP处的IP均为V≥VP情形下iP(V)的积分结果.当VP增大时,不同VG2情形下对iP(V)的积分随之减小,即对应的IP下降.或者说,当VP增大,可到达集电极热电子的数量减少,IP下降.图6所示的iP(VP)-VP能量分布结果展示了不同VG2下,IP随VP的变化情况,直观地解释了普遍现象2):随VP增大,IP-VG2曲线整体下移.

图6 不同VG2情形下iP(VP)-VP的能量分布
2.5 集电极电流IP峰(谷)随VP的变化分析
以图2中VP=4.50 V,分析IP-VG2曲线C峰所处范围iP(VP)-VP能量分布变化过程为例.图7显示了当VG2∈[33.91 V,36.74 V]时,iP(VP)-VP的实验结果,结果表明:在此范围内,iP(VP)-VP分布随VG2增大向VP高电位端移动且峰高逐渐上升.由此可见,由VP=4.50 V直线与iP(VP)-VP曲线在高电位端所围面积(即IP)随VG2的增大而增大,从而解释了图2中当VG2∈[33.91 V,36.74 V]时,IP随VG2逐渐上升的现象.

图7 IP上升侧iP(VP)-VP分布随VG2的变化情况
图8显示了当VG2∈[40.98 V,43.81 V]时,iP(VP)-VP的实验结果.在此范围内,随VG2增大,iP(VP)-VP分布峰也向VP高电位端移动,但是峰高明显下降.尽管在VP低电位端逐渐出现新能量分布峰,但VP=4.50 V直线与iP(VP)-VP曲线在高电位端所围面积(即IP)随VG2增大而减小.此过程与图2中当VG2∈[40.98 V,43.81 V]时,IP随VG2增大而逐渐减小的过程一致.
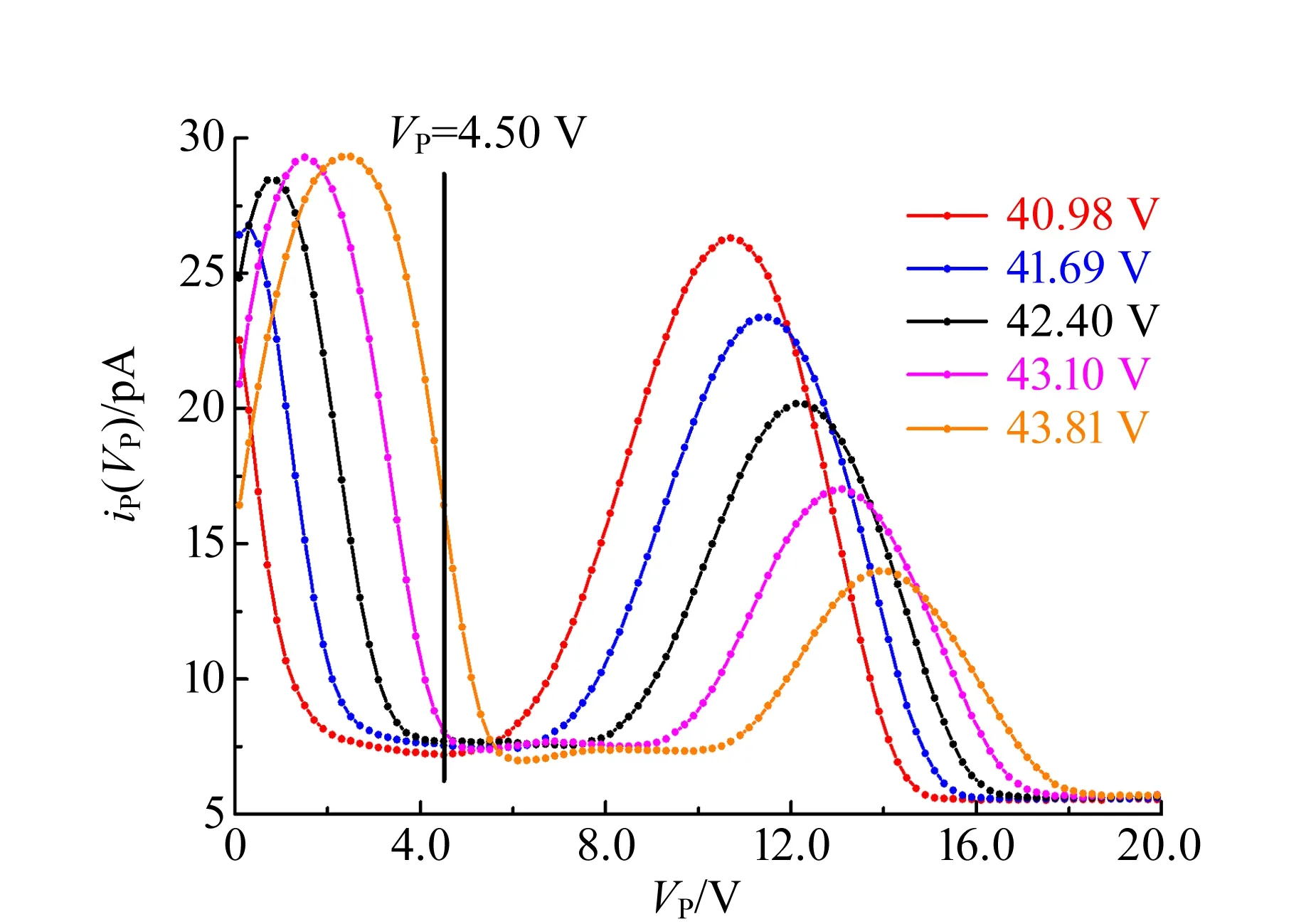
图8 IP下降侧iP(VP)-VP分布随VG2的变化情况
通过iP(VP)-VP实验事实,图7和图8分别说明了VP=4.50 V时,IP-VG2曲线C峰两侧IP变化的内在关联.结合上述分析,当VG2∈[37.44 V,40.27 V]时,必然存在IP峰值点.
图9显示了处于IP峰附近iP(VP)-VP分布随VG2的变化情况.针对不同VG2,在VP≥4.50 V区域iP(VP)-VP曲线与iP(VP)=0基线所围成面积为最大值,即为IP峰处电位VG2.
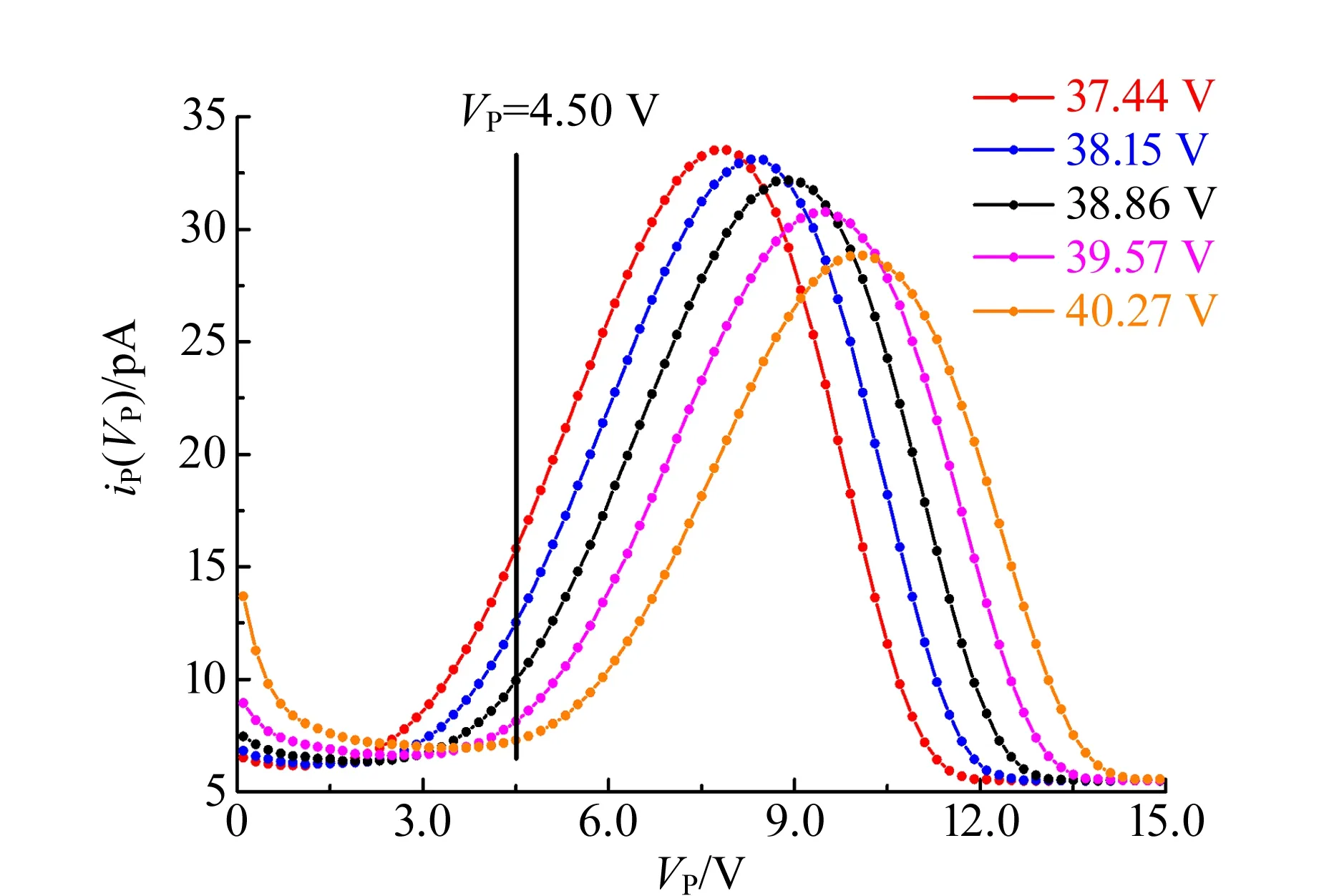
图9 IP峰附近iP(VP)-VP分布随VG2的变化情况
若VP增大,所有VG2下IP(VP)-VP曲线所围面积均变小,从而使IP-VG2曲线整体下移,对应普遍实验现象2).显然,不同VG2下的面积(即IP值)变化并非等量.以图2中曲线C峰为例,当VP增大时,对于VG2较小的情形,其iP(VP)-VP与VP在高电位端所围面积的减少数量也较多,因此最大面积也将出现在更高VG2的条件下,如图9所示.同理,图2中IP-VG2曲线的IP谷也随VP增大而出现在更高的VG2,上升侧和下降侧也都同步向高VG2方向移动.上述实验现象解释了普遍现象3):随VP增大,IP-VG2曲线中的IP谷电位或峰电位向VG2高电压端移动.
2.6 VP高于激发电位情形分析
从图6、图8和图9实验结果可见:iP(VP)-VP能量分布延伸到高于原子激发电位的VP高能端.到达集电极的热电子包含2种情形:
1)与管中原子完成能量交换和后续从灯丝发射出来,并在加速区获得足以“跨越”集电极电位的热电子;
2)能量满足却没发生交换,而在加速区又继续获得能量的热电子.
显然,高于激发电位的iP(VP)-VP分布主要来自后者.图2中IP-VG2曲线所记录的就是那些经过加速区抵达第二栅极时,还具有“剩余”能量足以“跨越”VP(阈值)的所有热电子的集体贡献.上述iP(VP)-VP实验事实表明:管中热电子具有能量分布规律且随VG2变化,并在与管中原子交换能量过程不断建立新的动态平衡分布.显然,即使VP高于激发电位,但其与iP(VP)-VP分布高电位端所围面积仍不为零,且随VG2变化.由此解释了普遍现象4):即使VP高于原子激发电位,仍可清晰地观测到IP-VG2的变化规律,如图10所示.
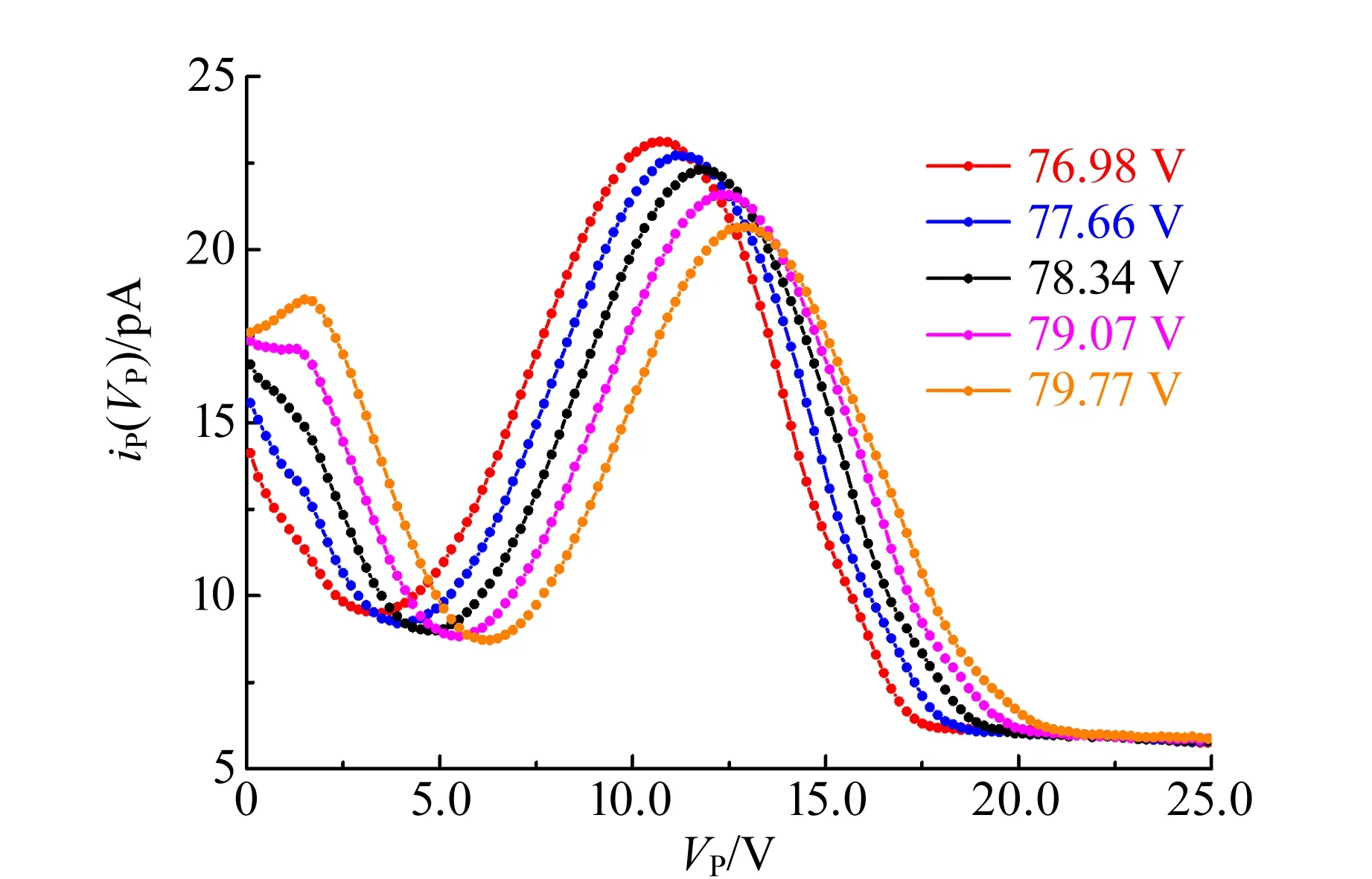
图10 VG2高电位端iP(VP)-VP的分布变化情况
图10结果表明:随VG2增大,高于激发电位的iP(VP)-VP占比也逐渐增大,意味着满足但没完成能量交换的热电子数量随VG2增大而增加(积累效应),因而出现普遍现象5):在VP恒定条件下,IP-VG2曲线随VG2增大呈现类周期振荡上扬.
2.7 微分电流iP峰周期与峰位和展宽
图5显示了处于VG2低电压端,随VG2逐步增大,iP(VP)-VP分布逐渐呈现出完整峰形分布.随VG2增大,峰处电位(能)往更高能量方向移动,这意味着热电子获得越来越多能量.
当继续增大VG2时,实验可观测到如图11所示的变化情况:当VP处于高电位,原有iP(VP)峰渐渐隐没,与此同时,在VG2的低能端,新的iP(VP)增峰缓缓呈现且逐步往VP的高能端移动.随着VG2继续增大,高能端iP(VP)峰热电子持续获得更多能量,直至激发管中原子而失去能量,从而使高能iP(VP)峰逐步消失.在这个过程中,从灯丝发射出来的后续热电子的能量也在持续补充,对应VG2的低能端新增iP(VP)峰也随之逐渐清晰.重复图3所示的初始阶段情况,图12实验结果验证了该物理过程.

图11 VG2增大时前峰缓缓隐没而后峰渐渐呈现

图12 VG2增大时iP(VP)-VP分布后峰完整显现过程
通过图5、图11和图12的实验结果,从iP(VP)和iP(V)-V能量分布变化规律的角度,分析了图2中IP-VG2曲线自A峰到B峰区间的物理过程.可以发现:iP(V)峰“形成—增强—激发—减弱—消失(伴随着新峰出现)”历程反映了热电子iP(V)-V能量分布的“生命”周期[1].显然,当VG2持续增大,iP(V)-V将进入下一个“生命”周期,周而复始.
图13显示IP-VG2曲线中B峰到C峰区间iP(VP)-VP能量分布重复着上述周期过程.由图13可以看出:
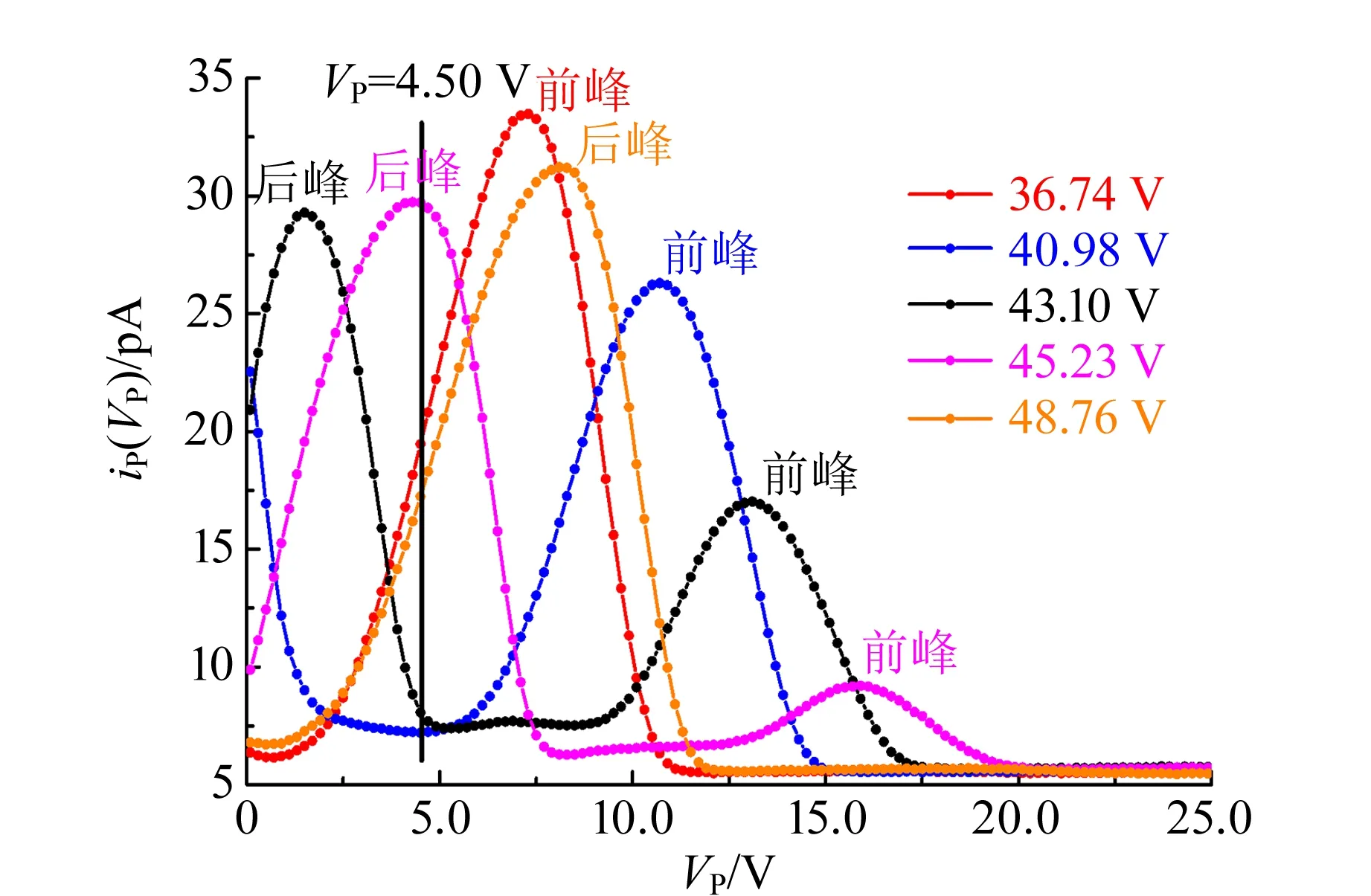
图13 VG2增大时iP(VP)-VP分布(峰)的“生命”周期
1)当VG2=36.74 V,iP(VP)-VP单峰(图中标记为前峰)完整呈现;
2)当VG2=40.98 V,前峰往VP高能端移动,且峰高下降,而低能端则出现1个新iP(V)-V能量分布(图中标记为后峰);
3)当VG2=43.10 V,前峰进一步往VP高能端移动,且峰高继续下降,随之低能端后峰逐渐形成;
4)当VG2=45.23 V,前峰持续往VP高能端移动,但峰强更弱,而后峰则逐渐增强;
5)当VG2=48.76 V,前峰消失,后峰完整呈现.
在此过程中,随着VG2逐步增大,持续发生原子激发而失去能量的热电子数量同步增加,从而前峰逐渐减弱直至消失.与此同时,后续从阴极发射出来(包括管中没有完成激发)的热电子,在VG2加速作用下逐渐形成新的iP(VP)-VP能量分布,即图13中后峰的成长过程.值得一提的是,在VG2=48.76 V处,后峰比在VG2=36.74 V处的前峰具有更高的峰位VP和更大的峰宽.图14显示了在VG2实验范围内全部出现iP(VP)-VP“完整”峰形的观测结果.结果表明:随VG2增大,后一个“生命”周期的峰位VP比前一个周期具有更高电位,且其峰宽也随之增大.

图14 热电子iP(VP)-VP分布峰形随VG2的变化
由于VG2采用步进而非连续改变,难以准确判断iP(VP)-VP分布完整单峰的起点电位(能).在图13中选用VG2为36.74 V和48.76 V处iP(VP)-VP分布峰,图14则选用VG2为36.03 V和48.06 V处的分布峰,2种情形下对应的iP(VP)-VP分布略有差异,但可从峰宽增大推断iP(VP)峰必然移向VP高能端.同理,尽管难以获得VG2为61.47,74.14和88.21 V情形下iP(VP)-VP分布的完整单峰,但通过峰宽可以推断峰位VP变化.
2.8 激发电位递增问题
上述实验结果表明:iP(VP)-VP能量分布只存在单峰和双峰2种形态.单峰描述没有发生原子激发情形的热电子能量分布;双峰反映伴随着原子激发(交换能量),后续从阴极发射出来热电子获得能量并形成新的动态平衡分布.
显然,当峰宽增大到一定程度,双峰之间也将出现部分交叠,从而无法得到清晰完整的单峰分布,如图14中VG2为74.14 V和88.21 V的情况.从图14中可见,单峰iP(VP)-VP分布峰位VP和峰宽随“生命”周期递进(或称“进化”)逐步增大,说明热电子达成单峰iP(VP)-VP分布的总能量(或平均能量)随“生命”周期递进而递增.从能量守恒角度,这意味着管中热电子需要获得比前一周期更多的能量,因此必须在比前一周期更高的VG2作用下才能实现新的完整单峰分布.
图13实验结果表明:完整单峰仅可能出现在没有发生原子激发的特殊情形.一旦发生原子激发,IP反映的是双峰变化的叠加结果.因此,常规方法所测得的IP-VG2曲线中每处VG2的IP既包含发生原子激发过程前峰变化,同时还可能包含后峰贡献.上述分析可知:原理上相邻2次纯完整单峰iP(VP)-VP能量分布所处的准确VG2差值即为管中原子激发电位.
常规方法则是在确定VP条件下观测IP-VG2的变化,以图13中VP=4.50 V情形为例.若以IP峰处为起点,随着产生原子激发,图中前峰渐弱,直至由VP≥4.50 V区域iP(VP)-VP面积(积分)所得IP达到最小;随后,由于区域内后峰渐强,IP也相应增大;直至VP≥4.50 V区域内前峰消失(或面积最小),而后峰面积最大,此时IP到达新峰值.由此可见,在任一VP情形下IP随VG2变化的实质为iP(VP)-VP能量分布随VG2变化过程的体现,由IP-VG2曲线相邻IP峰处的VG2差值可合理表征原子激发电位.
既然iP(VP)-VP分布峰宽随其“生命”周期递增,相应的IP(VP)峰位也逐渐移向VP高能端,那么在单峰分布范围内任一VP处观测IP-VG2曲线,两相邻IP峰对应的VG2差值也必然随之递增,如图15所示.

图15 相邻IP峰与iP(VP)单峰分布VG2差值递增情况
图15中横坐标n表示相邻IP峰或iP(VP)-VP单峰分布情形电位VG2差值的排序,且随VG2增大方向增加.其中,曲线1为表1中不同VP情形下相邻IP峰处电位VG2差值的同序平均结果,曲线2为图14中IP(VP)-VP单峰分布对应的VG2差值,VG2步进约为0.7 V(图中也考虑了差值的误差传递修正).尽管二者斜率有差异,但趋势一致,曲线1变化基本反映了曲线2的物理过程.
上述分析表明:IP-VG2曲线重复出现的IP峰反映了热电子iP(VP)-VP单峰能量分布的“生命”周期.由于iP(VP)-VP分布后峰比前峰具有更高峰电位能和更大能量范围,这意味着热电子想要从加速区获得更多能量将需要更高VG2,这就是IP峰电位VG2差值递增的内在原因.由此解释了普遍现象6):原子激发电位随VG2升高而逐渐增大(激发电位递增).
综合上述分析可知,尽管IP-VG2曲线清晰地展示了原子激发实验现象,但通过相邻IP峰电位VG2差值对激发电位的分析只是半定量分析.F-H实验测得的原子激发电位递增源于热电子具有能量分布且其展宽随加速电场增强而增大.值得一提的是,随着VP增大,在IP值中反映单峰分布占比减弱,而双峰分布组合占比增加.由此推断,当VP超出单峰分布范围或高于原子激发电位时,IP-VG2实验测量没有意义.
3 结束语
F-H实验物理内容丰富,是本科物理教学的重点实验项目,多种实验现象也已得到广泛关注并被分析讨论.本文通过在集电极电位VP施加微小调制ΔVP,利用锁相放大技术实现集电极电流微分iP(VP)测量方法.由一系列不同VG2情形下的iP(VP)-VP分布实验结果,解释了常规方法所观测到的普遍现象.实验发现:iP(VP)-VP能量分布仅出现单峰和双峰2种形态,其中单峰描述了发生原子激发前的热电子能量分布,双峰反映了伴随着原子激发(交换能量),在低电位端出现新的动态平衡分布.IP-VG2曲线的类周期振荡反映了iP(VP)-VP单峰和双峰交替出现的“生命”周期.根据能量守恒,需要更高加速电位(能)VG2才可形成完整单峰.通过iP(VP)-VP测量分析,有助于透彻理解F-H实验原理,以及测得激发电位递增现象的物理本质.
致谢:感谢复旦大学乐永康教授的交流.感谢中国科学技术大学孙腊珍教授的有益讨论.

