基于线结构光的轮胎胎胚外形检测

北京信息科技大学仪器科学与光电工程学院 刘杰 郭阳宽 张晓青

基于激光三角测量原理研制了轮胎胎胚外形轮廓检测系统。检测过程中由于激光传感器和待测物体间的相对位姿问题，可能导致检测结果产生误差。对此，本文设计了位姿调整算法进行姿态调节，首先利用胎胚的圆周特性确定理想结构光线条，然后使用理想结构光和实际结构光的位置分析，对三种常见偏差进行调整。最后系统扫描采集胎胚外轮廓点云数据，并利用贪婪投影三角化算法进行三维重建。实验结果表明，本检测系统能准确对轮胎胎胚三维轮廓进行还原。

随着我国交通事业的快速发展、行驶道路的改善以及车速的提升，对轮胎的质量提出了更高的要求[1，2]。但是，有研究表明目前市面所售新轮胎产品合格率大约为94%，意味着消费者有6%的几率买到原厂出产的质量不太合格的轮胎[3]。因此，对轮胎胎胚的质检工作迫在眉睫，而胎胚外形是质量检测中必不可少的部分。

传统检测采用人工的方式进行，该方式误差大且重复性低下。而基于激光测距原理的非接触式测量法却自动化程度高、精度可靠、稳定性好[4]。本系统基于该原理研制一种轮胎胎胚外形检测系统[5，6]，对激光传感器和待检测胎胚进行位姿调节计算[7]，以获得更高的准确度，最后利用贪婪投影三角化算法对采集胎胚点云进行三维重建[8]，以期直观地展示胎胚的外形。

1 检测系统框架结构

轮胎胎胚外形轮廓检测系统是由硬件机械结构和软件部分组成。硬件系统主要包括GOCATOR 线结构光传感器、伺服电机以及电机驱动设备，依据激光三角测量原理，设计本系统的结构，系统结构如图1 所示。

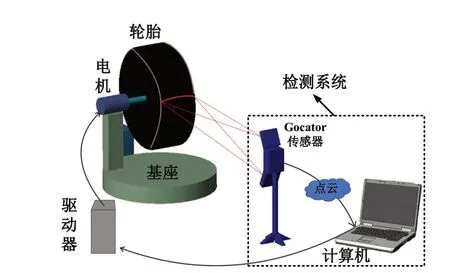
图1 系统结构设计Fig.1 System structure design

软件系统则是对线结构光传感器的SDK 进行二次开发，并利用VS 结合PCL 点云处理库编写。

2 传感器位姿调整

本系统使用的线结构光传感器为了扫描整体胎面轮廓，理想情况下应平行照射到胎面。但是，通过多次实验发现真实线结构光和理想线结构光之间会出现位置偏差，因此，需要对传感器的位姿进行调整。

2.1 理想线结构光查找

在首次测量的时候，由于待检测轮胎胎胚和结构光传感器的相对位置并不确定，因此无法定位理想结构光线条。为了实现在位姿校准过程当中，不利用辅助标志点查找待检测物上的理想线结构光位置。本文结合胎胚圆周特性，对胎面进行竖直检测，查找趋于理想状态的标准圆，该圆离线结构光传感器最近的点即为结构光平行照射下，理想结构光线条上的点。通过上述方式找出理想结构光的位置。

对采集到的数据进行圆的拟合，查找趋近于圆的结构光线条。采用最小二乘拟合的方式进行圆的拟合，竖直扫描并点云拟合标准圆如图2 所示。

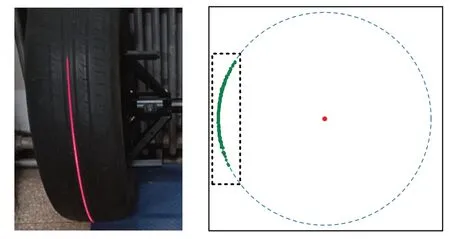
图2 扫描模式和点云拟合圆Fig.2 Scan pattern and point cloud fitting circle

通过上述方法，可以找到横向检测时的结构光在轮胎上的理想位置。此时，传感器转为横向扫描。转换过程中，为了保证实际结构光线条无限趋近于理想结构光，软件系统实时处理数据对当下位姿进行判断。

2.2 位姿偏差调整

线结构光传感器采集数据为三维坐标X、Y、Z，其中的X 代表结构光一维横坐标，Z 轴表示传感器到检测胎面的距离，Y 轴为系统采集频率。而结构光和待检测胎胚之间的常见的位置偏差及调整方式有如下几方面:

2.2.1 水平偏差计算

当出现水平方向上位置偏差时，传感器横坐标0 点左右两边的x值的个数不同。结构光偏左，负方向上的激光点未在胎面，即未在传感器工作范围内；结构光偏右，正方向上的激光点未在采集区间。因此，可以通过获取胎面数据上的x值的正负个数进行调节，计算水平方向的左右偏差。

调节公式如式（1）所示:

式（1）中，d为激光正负点个数差的绝对值，n表示的是激光点的个数。

2.2.2 仰角调整

理想线结构光位置的确定意味着传感器到待检测胎面的距离值z的确定，当实际线结构光在胎面位置过上或过下时，z值会变大，通过计算得出仰角的大小，对结构光进行角度调节，如式（2）所示:

式（2）中，z1为传感器到轮胎胎面的标准垂直距离，z2为存在位置偏移的线结构光传感器到胎面的距离，r0为轮胎的理想半径，θ为理想结构光和真实线结构光间的角度偏差。

2.2.3 倾斜角调整

当理想线结构光与实际线结构光之间产生倾斜夹角的时候，会导致结构光传感器不同的x值处所对应的轮胎圆不够统一，因此，通过反三角函数即可求出倾斜角度如式（3）所示:

式（3）中α为倾斜角的角度，x为结构光中心点到选定的待测点的值，Δz为理想线结构光和实际结构光线条在同一x值下所对应的距离之差。

3 轮胎胎面三维重建

采集到的数据均为传感器坐标系下的数据，为了进行直观显示，需要将原始数据转换到笛卡尔坐标系下。需先转换至极坐标系，转换关系如式（4）所示:

式（4）中，r0为轮胎的理论半径，z为传感器到待检测物的距离，z1为标准距离，n为转换过程中选取的任意点，φ为转换角度。

在坐标转换至三维笛卡尔坐标系后，为展示胎胚的三维外形特征，利用贪婪投影三角化算法进行三维重建。

4 实验结果验证

轮胎匀速旋转，结构光传感器扫描式采集胎面外形轮廓的点云数据信息，点云数据离散，对其进行三维重建，重建前后胎胚轮廓如图3 所示。

5 结论

通过线结构光传感器扫描胎胚轮廓点云数据，使用二乘拟合标准圆的方法，找到传感器和胎胚间的标准距离，再对传感器和待测胎胚间进行相对位姿调整，最后，使用贪婪投影三角化算法对采集到的点云三维重建，并通过实验验证了方案和算法的可行性。