燃气管道定向钻段与开挖敷设段无弯管连接

石丹阳, 黄 飚, 张 鸣, 陈赐铭, 段保伟

(1.中裕(河南)能源控股有限公司,河南郑州450000;2.中裕城市能源投资控股(深圳)有限公司,广东深圳518049)

1 问题的提出

1.1 无弯管连接

钢质燃气管道水平定向钻穿越段的出入土端与地面有一定夹角,在与开挖敷设段连接时,施工图设计多采用加设弯管的连接方式。施工中弯管连接需要按照开挖敷设段设计沟底(简称设计沟底)标高切除穿越段多余管头,加设弯管,与开挖敷设段连接。在具体施工过程中,小管径(一般DN 300 mm以下)、小出入土角的情况下,施工单位更倾向不加设弯管而利用管道自身柔性实现定向钻出入土端直线段与开挖敷设段的连接,即在出入土端直线段开挖一部分土方,利用管道自重形成的挠曲线,使管道下降至设计沟底,本文称该种连接方式为无弯管连接。弯管连接和无弯管连接见图1。

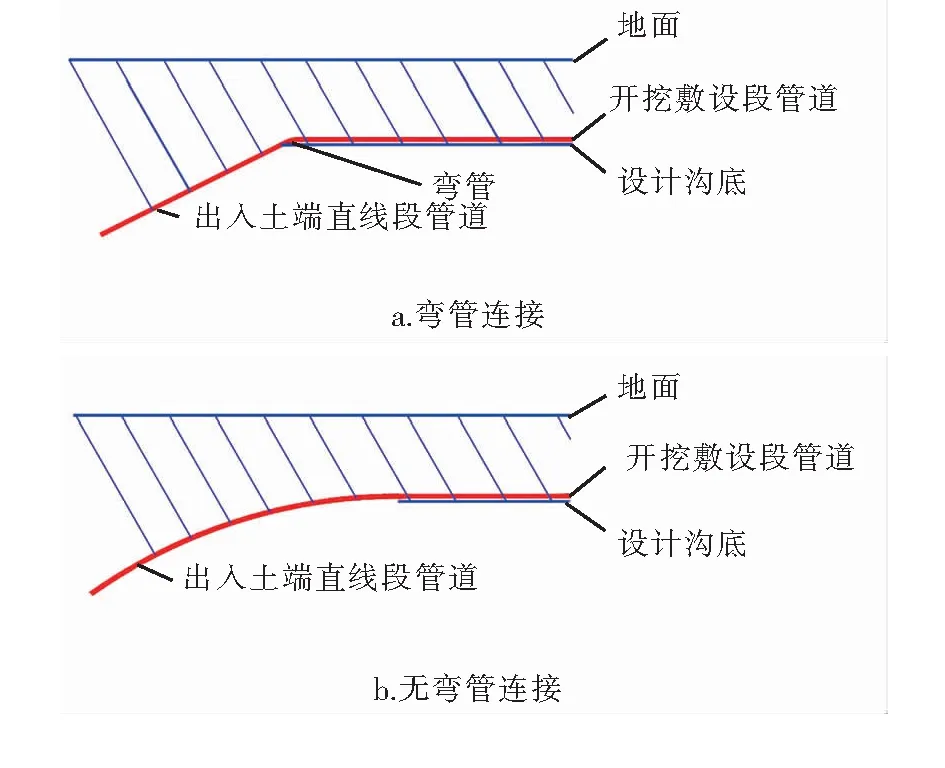
图1 弯管连接和无弯管连接

弯管连接需要精准切割管头,弯管的对口与焊接比直管道难度高,且对口与焊接均为2次。无弯管连接无须切割管头,对口及焊接难度降低且只需要1次。焊接完成后,还需要焊缝外观与无损检测,检测合格后,进行焊口防腐以及相关检测,然后回填。在出入土端直线段开挖虽然增加了一定的土方量,但施工仍较为简便,尤其适用于地下水位较高或土质较差、人员在沟底操作困难的地段。

1.2 问题的提出

GB 50251—2015《输气管道工程设计规范》第4.3.15条第2款要求,弹性敷设管道的曲率半径应满足管子强度要求,且不应小于钢管外直径的1 000倍,垂直面上弹性敷设管道的曲率半径还应大于管在自重作用下产生的挠度曲线的曲率半径。有设计单位根据此条规范,认为无弯管连接的曲率半径不能满足该要求,或经过沟通认为可在一定的小角度范围内采用无弯管连接,但建设单位已经采购的小角度弯管利用不上,造成浪费。

在施工现场,也出现了开挖量不足、定向钻穿越段管道不能下降到沟底、采用挖机下压悬空管道导致管道变形的事故。施工单位现场经验存在一定局限性,施工阶段控制指标仅为管道自然下降至沟底时管道无可见变形,对于管道通气后特别是高压管道,在相应的安全系数下,是否能够保证安全使用以及各项管道结构计算是否在安全范围内,均未考虑。

现阶段尚无明确的计算方法,来判断无弯管连接在各项参数条件下的适用范围,以及计算得出安全范围内的开挖长度。

本文通过对无弯管连接的特点分析,选择相应的计算模型,给出完整的结构计算方法,判断无弯管连接适用范围并计算最小开挖长度。需要说明的是,本文主要讨论的是钢质管道,相关参数与计算主要依据GB 50251—2015、GB 50423—2013《油气输送管道穿越工程设计规范》。

2 无弯管连接参数、计算模型选取

2.1 定向钻曲率半径、小角度与小管径范围

① 定向钻曲率半径、小角度范围

GB 50423—2013第5.1.2条和第5.1.3条规定,穿越管段曲率半径不宜小于1 500倍钢管外直径,且不应小于1 200倍钢管外直径。入土角宜为6°～20°,出土角宜为4°～12°,较小的出入土角度有助于降低回拖力及连接施工难度。结合施工现场实际,本文认为出入土角构成的直角三角形(见图2)中,出入土角α的邻边长度偏差p小于等于0.01为小角度。

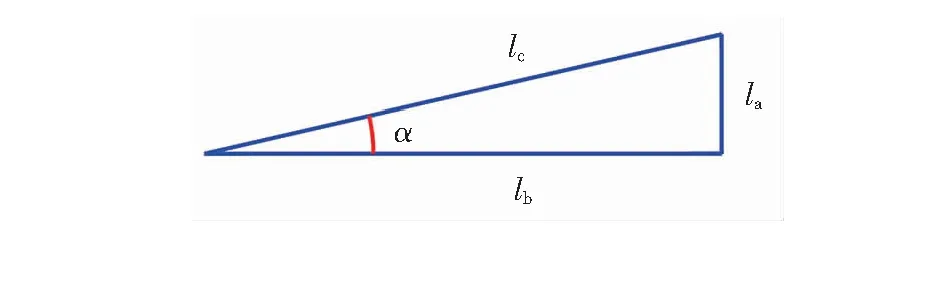
图2 出入土角构成的直角三角形

图中α——定向钻出入土角,(°)

la——α对边长度,m

lb、lc——α的2条邻边长度,m

p的计算式为:

(1)

式中p——出入土角α的邻边长度偏差

由式(1)计算得出α≤8.11°,因此本文定义出入土角4°～8°为小角度范围。在一般定向钻的设计深度(一般不小于3～4 m)下,按照轨迹计算方法[1],在出入土角为4°～8°,穿越管段曲率半径不宜小于1 500倍钢管外直径,且不应小于1 200倍钢管外直径的参数下,定向钻在出入土点至底部直线段的轨迹,与管道自重形成的挠曲线相比,可近似认为是直线以简化计算,下文对这种简化计算的误差结合实际进行了分析,可满足工程计算需求。

② 小管径范围

根据管道在实际施工中柔性特点以及下文的理论计算,取DN 300 mm及以下管径为小管径,现阶段管道特别是高压管道的小管径一般为DN 200～300 mm,壁厚为6.3～9.5 mm。由于管径较小,为方便计算,取管道轴线代替管道进行相关几何量计算,不考虑管径对几何量计算的影响。

2.2 几何模型的建立

为方便计算,建立几何模型计算坐标系,见图3。设计沟底深度为h,点B为定向钻管道与地面线的交叉点,坐标为(0,h)。点C为定向钻管道可自然下降到设计沟底的管端,点C横坐标可能大于、等于或小于0。点C横坐标大于0时,自然下降到设计沟底的位置为C′;点C横坐标小于0时,自然下降到设计沟底的位置为C″。点N、C之间为悬空段。点N为定向钻管道悬空段与钻孔内段的分界点。点N横坐标绝对值为从出入土端向定向钻方向开挖的长度。图3中绿色曲线段为NC′,紫色曲线段为NC″。点A位于定向钻出入土直管段并处于钻孔中。

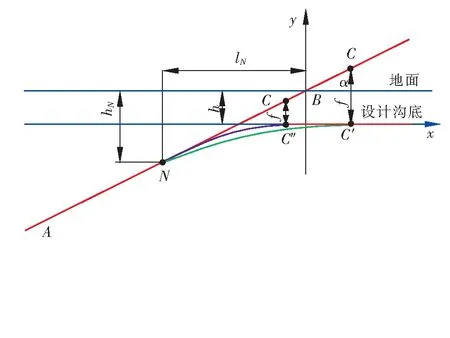
图3 几何模型计算坐标系

直线ABC的方程为:

y=tanα·x+h

(2)

2.3 约束特点及梁计算模型选取

① 定向钻段约束特点

计算埋地燃气管道弹性敷设弯曲变形量时,一般采用材料力学中的梁模型[2]。开挖敷设段覆土之后,覆土对于管道有一定嵌固作用,根据GB 50251—2015第4.3.15条及条文说明,连续开挖敷设段约束处于简支梁与固定梁的中间状态。简支梁一端为固定铰支座,另一端为可动铰支座;固定梁两端均为固定端[3]92-93。典型的定向钻管道主体近似为U字形,扩孔后定向钻孔径一般为管道外直径的1.2～1.5倍[1],管道轴向位移不受钻孔约束。

② 计算模型选取

向定向钻方向开挖一定距离后,部分定向钻管段悬空,在小角度下,近似成为伸臂梁。根据孔内管道约束特点,采用简支单侧伸臂梁模型[4]进行计算,见图4。图3中的点A、N、C与图4相对应。

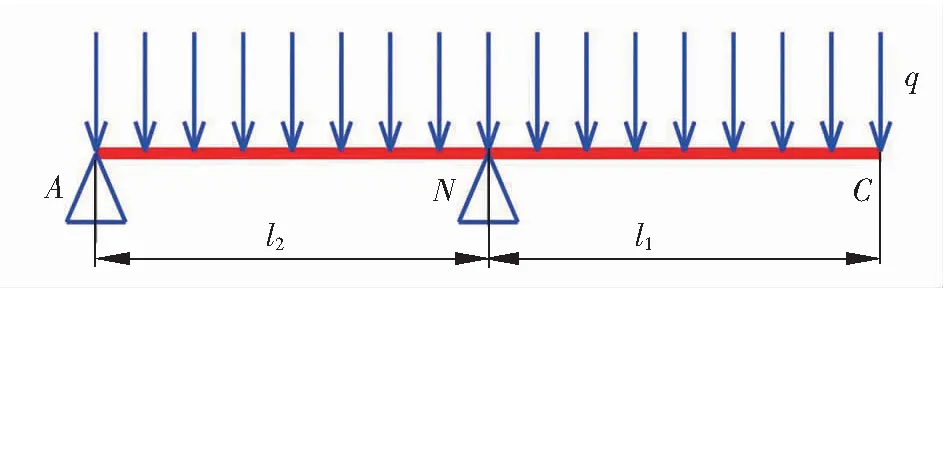
图4 简支单侧伸臂梁模型

根据简支单侧伸臂梁模型,结合钻孔内管道约束特点,孔中支座A反力最小为0且不能为负值。取支座反力为0的点为点A,有l1=l2=l,最大弯矩出现在点N,最大挠度位于点C,点N弯矩与点C挠度计算式为[3]131,[4]:

(3)

(4)

(5)

(6)

式中M——点N弯矩,N·m

q——单位长度管道自重荷载,N/m

l——悬空段长度(点N、C间距离),m

f——点C挠度,m

E——钢材弹性模量,Pa,2.06×1011Pa

I——钢管的惯性矩,m4

D——钢管的外直径,m

d——钢管的内直径,m

ρ——钢材密度,kg/m3,为7 850 kg/m3

g——重力加速度,m/s2,为9.8 m/s2

实际施工过程中对管道点C挠度进行测量,与计算值进行对比,见表1,相对误差计算以计算值为真值。

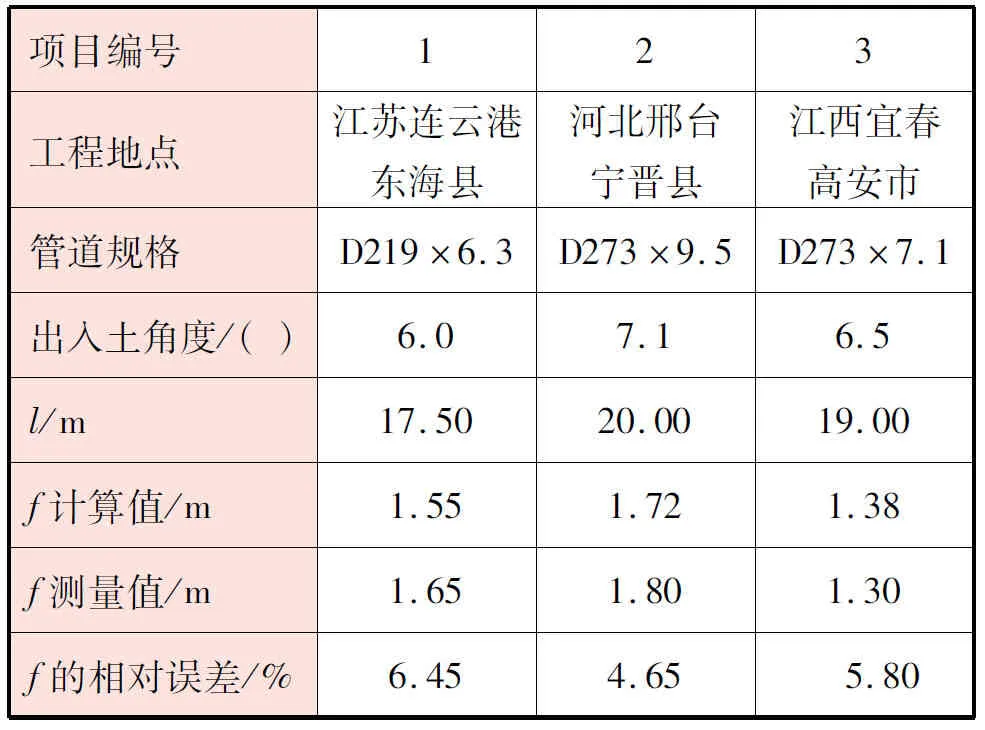
表1 点C挠度计算值与测量值对比

根据实测,考虑了现场的测量误差、钻孔不能形成严格意义的简支梁支撑,以及钻孔在泥浆浸润之后在管道作用下会产生一定的变形等因素,认为采用该计算模型仍能够满足工程计算精度。

对不同规格的钢管进行挠度计算,见图5。从图5可知,管道外直径越小,同样悬空段长度下挠度越大;悬空段长度超过15 m后,挠度增大明显。

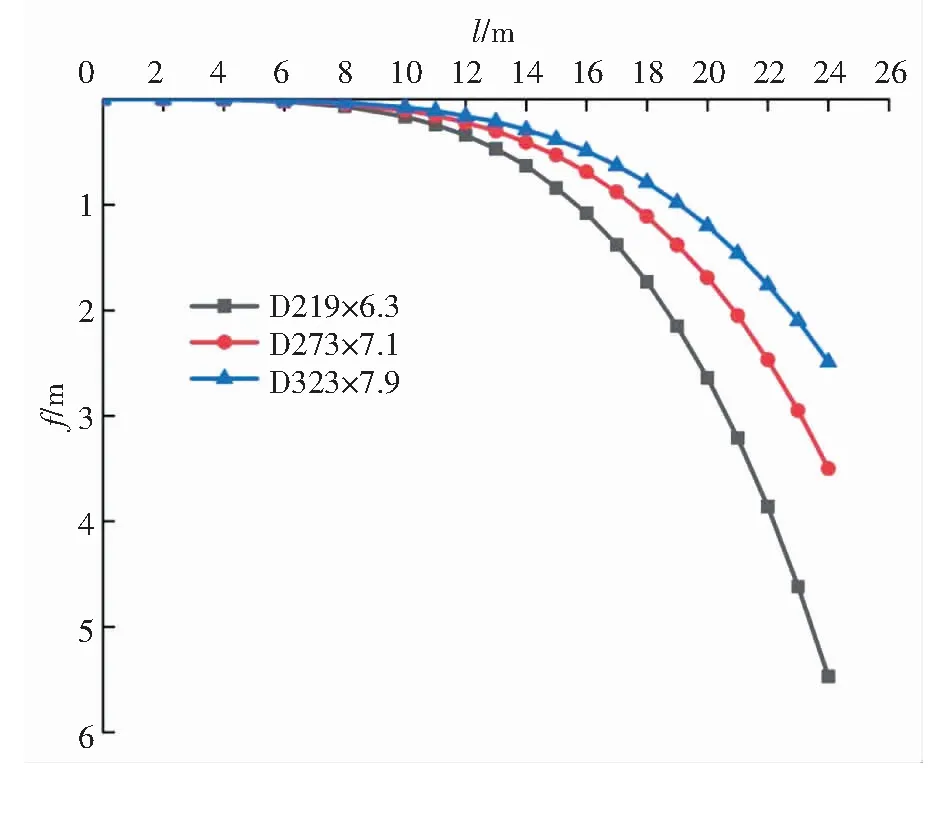
图5 不同规格钢管的挠度随悬空段长度的变化

3 计算与分析方法

为求最小开挖长度,假设点C横坐标,求出相关几何量,进行结构计算,需满足结构计算要求。如不满足,则根据结构计算结果调整点C横坐标,直至满足结构计算要求为止,此时的开挖长度为最小开挖长度。

3.1 几何量计算

根据图3可知,点C自然下降到设计沟底需要的挠度与点C纵坐标相等,即有:

f=yC

(7)

式中yC——点C纵坐标,m

根据挠度f由式(4)计算悬空段长度l,计算式为:

(8)

需要由点B向定向钻方向沿x轴开挖的长度计算式为:

lN=l-xC

(9)

式中lN——开挖长度,m

xC——点C横坐标,m

点N的开挖深度计算式为:

hN=tanα·lN

(10)

式中hN——点N的开挖深度,m

3.2 结构计算

① 应力计算式

根据上文可知,定向钻管道轴向位移不受钻孔约束,根据GB 50423—2013第4.4节,不需要计算温度变化引起的轴向应力和轴向稳定性,重点为强度计算。根据GB 50423—2013第4.4.2条,定向钻管道组合轴向应力(由内压产生的轴向应力与弯曲产生的轴向应力组成)、环向应力、弯曲应力计算式分别为:

(11)

(12)

(13)

式中σa——组合轴向应力,MPa

p——设计压力,MPa

δ——管道壁厚,m

σb——弯曲应力,MPa

σh——内压产生的环向应力,MPa

R——弯曲段曲率半径,m

弯曲应力的计算,可采用式(13),也可采用材料力学中弯矩与抗弯截面系数计算[3]126-136,两种计算方法本质相同。采用材料力学中弯矩与抗弯截面系数计算的计算式[3]136为:

(14)

(15)

式中W——钢管的抗弯截面系数,m3

式(14)中,弯曲段管道外侧为拉应力取正值,内侧为压应力取负值。按照最不利条件,校核许用应力时组合轴向应力计算式中弯曲应力取正值,校核当量应力时组合轴向应力计算式中弯曲应力取负值。

② 应力校核

根据GB 50423—2013第3.2.2条、第4.4.2条、第4.4.3条,轴向应力、环向应力、当量应力校核公式为:

[σ]=FΦσs

(16)

(17)

(18)

(19)

式中 [σ]——许用应力,MPa

F——强度设计系数

Φ——钢管焊缝系数,取1

σs——钢管最小屈服强度,MPa

σe——当量应力,MPa

当式(17)、(18)、(19)均满足时,应力校核通过。

3.3 开挖长度和开挖深度确定

采用多次试算的方法,确定开挖长度和开挖深度。具体计算步骤如下。

① 基本参数计算。设计压力、钢管钢级、管道规格、地区等级、定向钻出入土角度、开挖敷设段沟底深度等参数已知时,根据式(5)、(6)、(15),计算得到单位长度管道自重荷载、惯性矩、抗弯截面系数。

② 假设能够自然下降到开挖敷设段沟底的点C初始横坐标为0,根据式(2)、(7)计算得到点C挠度,根据式(8)计算得到悬空段长度,根据式(3)得到弯矩。

③ 按照式(17)～(19)进行应力校核,并判断是否满足应力校核要求。

④ 若不满足应力校核要求,应减小假设的点C横坐标,重复步骤②～③;若满足应力校核要求,同时有一定余量,可增大假设的点C横坐标,重复步骤②～③。

⑤ 试算一定次数后,得到刚好满足应力校核要求的点C横坐标,采用该值根据式(9)～(10),确定最小开挖长度与最小开挖深度。

4 算例及分析

4.1 算例

某城镇燃气高压管道项目,设计压力4.0 MPa,采用L360N无缝钢管,管道规格为D273×7.1,单位长度管道自重荷载为456.0 N/m,最低屈服强度360 MPa,地区等级二级,强度设计系数0.6,许用应力216 MPa,定向钻出入土角5°,开挖敷设段沟底深度1.6 m。定向钻段与开挖敷设段拟采用无弯管连接方式,计算最小开挖长度与最小开挖深度。算例采用的管径、壁厚、材质、设计压力、出入土角度、开挖敷设段沟底深度等具有一定的代表性。

算例中历次试算结果见表2。

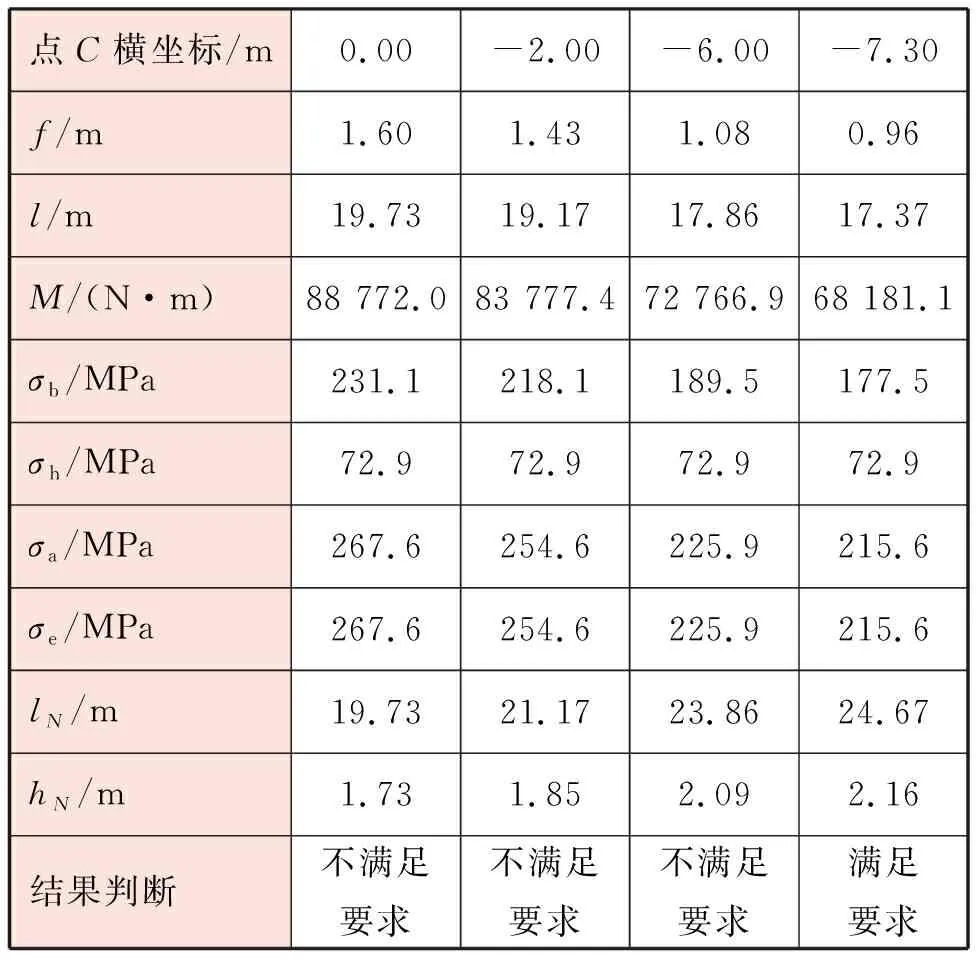
表2 算例中历次试算结果

经过一定次数的试算得知,-7.30 m是满足结构计算要求的点C横坐标,此时需要向定向钻段开挖长度为24.67 m,开挖深度为2.16 m。

4.2 相关分析

① 弯曲应力为组合轴向应力与当量应力的主要组成部分

设计压力不变,内压产生的环向应力与轴向应力保持不变,组合轴向应力或当量应力超标的情况均由弯曲应力过大造成。要满足结构计算要求,应控制弯曲应力,也就是要控制弯矩,弯矩与挠度的0.5次方成正比,最直接的方法是向定向钻段开挖,减小挠度。

② 许用应力为关键因素

算例采用了较为常见的钢级,强度设计系数为0.6。在城镇燃气工程中,在高压A设计压力下,三级、四级地区是较常见的地区等级,若采用0.3～0.4的强度设计系数,L360管材的许用应力仅有108～144 MPa,通过应力校核较难。因此当许用应力较低时,该种连接方式应经过计算校核满足相关要求后使用。

③ 壁厚的影响

为验证不同壁厚对计算结果的影响,仍采用上述算例参数,仅改变壁厚分别为6.3、7.1、9.5 mm进行计算,计算结果见表3。表3表明,不同壁厚对计算结果影响较小,不是主要影响因素。

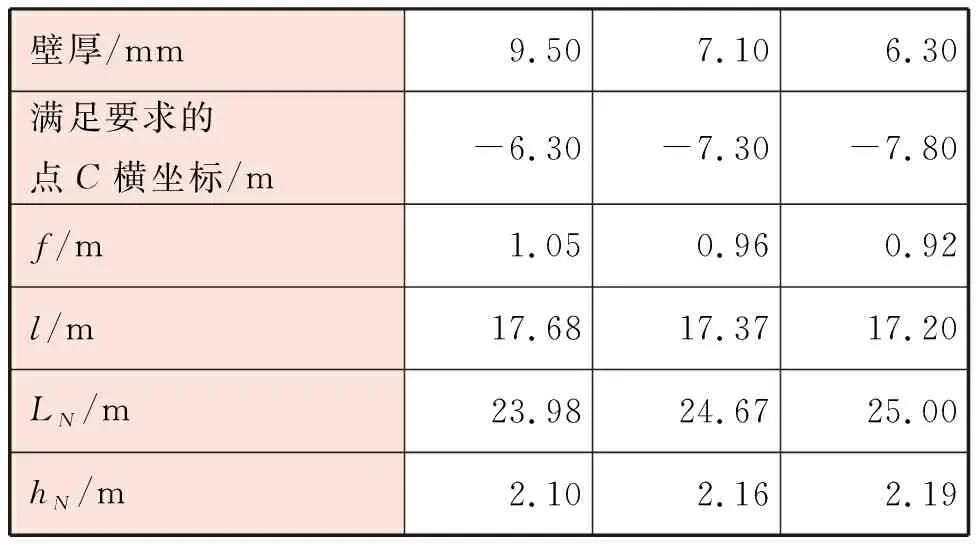
表3 不同壁厚的计算结果

5 结论

① 在小管径、小出入土角情况下,定向钻段与开挖敷设段无弯管连接方式有一定的简便性。根据约束特点分析,选择采用简支单侧伸臂梁模型来计算挠度与弯矩,根据工程实测值与计算值比较得知,挠度计算能够满足工程计算精度要求。

② 在管道公称直径不大于300 mm、出入土角为4°～8°的情况下,给出了定向钻段与开挖敷设段无弯管连接方式的结构计算与最小开挖长度的计算方法。

③ 弯曲应力是组合轴向应力以及当量应力的主要组成部分,许用应力为判断该种连接方式可行性的关键影响因素。

④ 当许用应力较低时,无弯管连接方式应经过严格计算校核后使用。