基于卷积稀疏编码与生成对抗网络的图像超分辨率重建
杜均森, 郭杰龙, 俞辉, 魏宪
(1.福州大学 先进制造学院, 福建 泉州 362000;2.中国科学院 福建物质结构研究所, 福建 福州 350108;3.中国科学院 海西研究院 泉州装备制造研究中心, 福建 泉州 362000)
1 引言
图像超分辨率重建是通过某种映射将低分辨率(Low Resolution,LR)图像重建出具有丰富细节的高分辨率(High Resolution,HR)图像的技术[1],在许多领域中得到广泛的应用,例如视频网络、眼底影像处理和卫星遥感等。目前主流的图像超分辨率重建算法主要可以分为两大类:基于传统的算法[2]和基于学习的算法[3]。传统算法包括基于插值和基于重建的算法,在图像超分辨率上取得了一定的效果。其中,基于插值的算法包括最近邻插值、双线性插值[4]、双立方插值[5]等,只是简单地增加对像素点,并没有充分利用图像的先验信息,难以恢复图像细节;基于重建的算法[6]包括凸投影集算法[7]和迭代反向投影算法[8],这类算法需要明确的先验信息并增加一些附加操作,导致计算量较大,效率较低。因此基于传统的超分辨率重建算法仍未能满足人们对图像分辨率提升的期望。
基于学习的算法通过机器学习算法学习到先验知识,能够更准确地捕获低-高分辨率图像特征之间的映射关系,从而极大地提升超分辨率重建的效果。目前常用的基于学习的算法主要有稀疏表示和深度学习。图像的稀疏表示作为先验知识,可以揭示图像的主要几何结构特征和分布,更有效地表示图像和保留高频结构信息,能够胜任各种视觉任务,例如人脸识别[9]、超分辨率重建[10]和去噪任务[11]等。Yang等人[12]认为不同分辨率图像的稀疏表示应当线性一致,通过学习高分辨率图像和相应的低分辨率图像之间的字典对获取对应的稀疏表示,利用稀疏表示恢复缺失的高频信息,进而重建出超分辨图像。Zeyde等人[13]在Yang的基础上对特征提取算子进行了改进,通过采用字典学习算法学习字典,并使用正交匹配追踪法进行稀疏求解。基于稀疏表示的超分辨率重建技术已经较为成熟,稀疏表示可以提供足够的图像高频信息,且具有较强的噪声抗干扰能力。稀疏编码虽然在重构图像上有着优秀的表现和深刻的物理意义,但其仍具有计算开销大、训练时间长的问题。
卷积神经网络已经成为有效解决许多具有挑战性问题的工具[14],在安防监控、光学成像[15]、全息投影[16]等领域得到广泛的应用。因此,学者们开始研究如何利用效率更高的卷积神经网络进行超分辨率重建,如SRCNN(Super-Resolution using Convolutional Nerural Network)[17]、VDSR(Super-Resolution using Very Deep Convolutional Networks)[18]、ESPCN(Efficient Sub-Pixel Convolutional Nerural Network)[19]等。近年来,文献[20]采用更深的网络并加入残差模块。文献[21]提出了一种融合多尺度特征的光场超分辨网络以提高光场子孔径图像的空间分辨率,进一步推进卷积神经网络在超分辨率重建技术的发展。这些深度学习模型可以学习到低分辨率图像到高分辨率图像的映射关系,但由于损失函数广泛采用岭回归以提高峰值信噪比,使得重建图像整体趋于平滑和缺失高频信息,重建效果尚不尽人意。而目前大多基于稀疏编码的超分辨率重建算法在图像输入时,首先将图片划分为具有重叠的小块,然后再对每个小块单独进行处理。然而这样的处理方式往往容易导致图像块之间的像素缺乏一致性和重叠像素中出现伪影,使得重建图像质量下降。近年来在深度学习领域中,结合稀疏编码的研究主要围绕数值优化算法操作的网络架构设计。文献[22]提出了可学习的迭代阈值算法,将迭代阈值算法[23](Iterative Shrinkage Thresholding Algorithm,ISTA)展开为深度神经网络。Liu等人[24]将可学习的迭代阈值算法应用于图像超分辨率重建领域。文献[25]将卷积稀疏编码转化为深度卷积神经网络并应用于图像的去噪和修复中,获得了不错的效果。
随着各类深度学习模型的提出和训练策略的不断完善,Goodfellowt等人[26]提出的生成对抗网络(Generative Adversarial Networks,GAN)采用了内容损失函数和对抗损失函数进行训练,使得生成图像更逼近自然图像。随后,Ledig等人[27]提出了SRGAN(Super-Resolution Generative Adversarial Networks),首次将GAN思想应用于图像超分辨率重建中,设计新型的感知损失作为网络的损失函数,使得重建图像更符合人眼的主观感受。Wang等人[28]提出ESRGAN(Enhanced Super-Resolution Generative Adversarial Networks),在SRGAN模型框架上加入了密集残差块并去除所有的批归一化层,同时加入了Relativistic GAN的鉴别器,使得重构图像具有更高的指标值和更清晰的视觉效果。基于生成对抗网络的图像超分辨率重建模型通过生成器与鉴别器的博弈可以生成逼真的重建图像,极大地改善了主观质量,但它们仍存在伪影,锐化后不可避免地产生噪点。
针对上述问题,本文提出了基于卷积稀疏编码和生成对抗网络的超分辨率重建模型。不同于以往可学习的稀疏编码模型采用全连接层实现稀疏编码,本文利用卷积算子替代稀疏编码算法中的矩阵乘法以获得图像的稀疏编码,既提高了网络训练的速度,又能够利用稀疏编码捕获图像的高频信息,提高模型对图像复杂几何结构的稀疏表示能力。随后获得的稀疏表示通过重建层生成重建的高分辨率图像。将重建图像与原始的高分辨率图像输入到鉴别器进行鉴别,使重建图像在低层的像素上和高层次的抽象特征上更好地接近原始的高分辨率图像,进一步提高了重建图像的质量。
2 理论基础
2.1 稀疏编码
信号的稀疏表示模型具有捕获信号奇异性结构能力强、表示冗余度低及系数稀疏度改的优势[29]。利用图像的稀疏表示作为先验知识,更有效地表示图像和保留高频结构信息。稀疏编码理论[13]即假设信号x∈Rm可以由字典中D∈Rm×n的原子线性组合来表示,其中m≫n,常见的稀疏编码模型如下:
其中:ϕ∈Rn表示稀疏编码,ε∈Rm表示信号重建后的残差。稀疏编码的目标函数如式(2)所示:
式中:第一项为重构误差;第二项为稀疏正则函数,用于测量和约束稀疏表示ϕx的稀疏性,常见的有ℓ0范数、ℓ1范数、ℓp范数(0<p<1)。对于公式(2),已经提出一些算法求解,包括正交匹配追踪[30]、K-SVD算法[31]和迭代阈值算法[23]。
迭代收缩阈值算法是一种在图像生成领域中非常受关注的算法。对于公式(2),ISTA[23]具体求解稀疏表示的迭代公式如式(3)所示:
式中:Sθ(x)为软阈值操作函数,θ为阈值,在公式(3)中,αλ=θ;sign(x)为符号函数。
2.2 生成对抗网络
生成对抗网络是通过对抗训练的深度学习模型。生成对抗网络由生成器(Generator,G)和鉴别器(Discriminator,D)两个网络框架构成。生成器G的主要目的是生成一张接近于真实的虚假图像来骗过鉴别器。而鉴别器D则是一个二分类器,目的是能够准确判断输入的样本是真实的还是生成器生成的虚假图像。生成器G与鉴别器D通过不断的对抗训练更新优化各自网络能力。总的损失函数如式(5)所示:
其中:pdata(x)为真实样本分布,p(z)为生成器生成图像的分布。生成对抗网络的训练是单独交替迭代训练的。对于鉴别器的优化,如式(6)所示,保持生成器G不变而训练鉴别器D,鉴别器的目的在于能够正确地区分真实样本和生成的虚假样本,使用1和0来代表输出的结果为真实样本和生成的虚假样本。第一项输入样本来自真实数据,因此期望D(x)接近于1。同理,第二项的输入样本来自生成器G生成的数据,因此期望D(G(z))接近于0,使得总数最大。
3 模型框架
本文采用基于卷积稀疏编码网络作为生成器,利用卷积稀疏编码层学习到低分辨率图像的稀疏表示ϕx,随后稀疏表示ϕx经过线性变换层映射得到高分辨率图像的稀疏表示最后再经过卷积字典层得到重建图像。为使最后重建图像更加自然,将生成的高分辨率图像与原始的高分辨率图像输入到鉴别器中,通过交替训练生成器和鉴别器,最后得到生成的高分辨率图像。模型的整体框架如图1所示。
3.1 生成模型
目前低分辨率图像数据集主要通过原始的高分辨率图像数据集经过下采样获取。在下采样的过程中,获得的低分辨率图像在一定程度上引入噪点,导致后续进行超分辨率重建时噪点被放大。而图像信号具有冗余结构,在稀疏编码过程中可以被稀疏化,噪声因其自身的随机性不能被稀疏表示。因此可以通过提取图像的稀疏表示,再用提取的稀疏表示来重构图像。在这个过程中,噪声被处理为观测图像和重构图像之间的残差,在重构过程中残差被丢弃,从而避免重建图像噪点增多的问题。
其中:{xi}为低分辨率图像集,{yi}为高分辨率图像集为稀疏性。λ∈R+对稀疏性进行加权,为避免D∈ς(m,k),F∈ς(l,k)在稀疏编码过程中的尺度模糊问题,ς(a,b)应满足:
式(8)中的稀疏性常用ℓ1范数来度量,即给定的信号x在字典D上的稀疏编码可通过求解以下优化问题得解:
由信号的稀疏表示模型可知,理想的低分辨率图像表示为x=Dϕx,高分辨率图像表示为y=Fϕy。在超分辨率重建中,通过稍微修改符号,ϕxi(D):xi↦ϕxi,ϕyi(F):yi↦ϕyi分别表示在字典D和F的稀疏解。对于公式(3)的稀疏求解则有:
与以往的稀疏编码不同,本文提出的框架直接输入整张图像处理,而不是对图像进行分块处理后再输入模型中。利用卷积算子代替矩阵乘法操作,卷积的滤波器作为字典,提取图像的特征信息。本文将ISTA的迭代过程展开为一个递归的卷积神经网络,如图2所示,每一层实现一次的迭代:

图2 卷积稀疏编码模块Fig.2 Convolutional sparse coding module
低分辨率图像在经过K个卷积稀疏编码模块的迭代后,学习到低分辨率图像的稀疏表示ϕ(D),其中K=12,本文将在4.1节中通过相关实验证明在K=12时得到的结果最佳。
Yang等人[12]提出并证明了不同分辨率的图像结构(稀疏表示)具有线性一致性。本文采用线性转换层Α来保证源图像和目标图像的稀疏表示的一致性,即允许高度稀疏的结构进行稀疏向量的线性变换:
其中ηi为误差。在得到低分辨率图像的稀疏表示ϕx(D)后,将其通过线性转换层A映射为ϕy(F),最后通过重建模块得到重建图像Y。如图3所示,重建模块通过卷积层、子像素卷积层(Pixel-Suffle)和激活层PReLU实现:
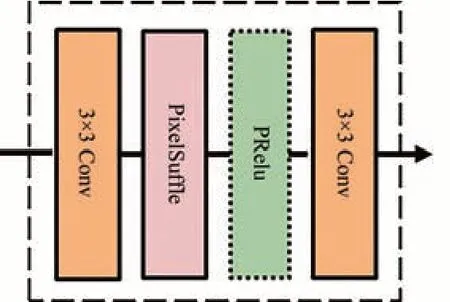
图3 重建模块Fig.3 Reconstruction module
基于卷积稀疏编码的生成器结构如图4所示,重建模块的数量N由放大倍率决定,即N=2或4,生成网络中均使用大小为3×3的卷积核。
图4 基于卷积稀疏编码的生成器结构Fig.4 Generator structure based on convolutional sparse coding
3.2 鉴别器网络
基于传统的卷积神经网络算法虽然在指标值上有很好的表现,但由于使用岭回归,重建图像的视觉图像有涂抹感。为解决以上问题,利用鉴别器网络评估生成器生成图像,通过引入对抗损失来激励,可以使重建图像更自然,减少涂抹感。鉴别器的设计遵循DCGAN设计原则,即取消池化层,同时使用LeakyReLU激活函数和批规范化(Batch Normalization,BN)。整个鉴别器网络框架主要有8个卷积层,由3×3卷积核和4×4卷积核的卷积层交替构成,卷积步长分别为1和2,卷积核数量由64逐渐增加到512。在得到输入图像的高层次特征后,将其进行维度变换后输入两个全连接层,Sigmoid激活函数得到真实或虚假的概率。具体框架图如图5所示,图中括号中的数字从左到右分别表示卷积核数量、卷积核大小以及卷积步长。

图5 鉴别器网络结构Fig.5 Discriminant network structure
3.3 损失函数
本文框架的损失函数在SRGAN的基础上进行改进,除了常用的图像均方值损失函数,加入对抗损失、感知损失以及稀疏损失,进一步提高模型重建能力。
对抗损失表示为鉴别器判出重建的高分辨率图像为真实样本的概率,旨在使生成器重建的图像能够愚弄鉴别器蒙混过关,公式如式(15)所示:
式中:ILR为输入的低分辨率图像,GθG(ILR)为重建的图像,DθD(GθG(ILR))为鉴别器判定生成器生成图像为真实图像的概率。
感知损失表示为重建图像与原始高分辨率图像在经过卷积神经网络提取图像特征的损失,避免最终的重建图像过于平滑。本文所用的卷积神经网络为VGG(Visual Geometry Group)[32],公式如式(16)所示:
式中:IHR为输入的原始高分辨率图像,i和j分别表示第i层最大池化前的第j个卷积层,φi,j表示通过VGG网络的第i层最大池化层和第j层卷积层之后提取的特征图,H和W为图片的宽和长。
稀疏损失旨在使获得的稀疏编码能够保留更完整的高频结构信息,公式如式(17)所示:
式中:均方误差MSE(x,x̂)为原始高分辨率图像和重建图像像素之间的损失;x表示原始的高分辨率图像;x̂为重建图像,并通过ℓ1范数‖ϕx‖1来约束其稀疏性;ϕx为图像的稀疏表示;β=0.6。
4 实验与分析
4.1 实验数据集
本文实验在Linux操作系统、深度学习框架Pytorch上完成,主要在低分辨率图像进行2倍和4倍的超分辨率重建实验。为了验证本文所提网络的性能,在通用的公开图片数据集上进行实验。训练集采用DIV2K和Filckr2K,两数据集图像分辨率均为2 048×1 080。DIV2K数据集包含1 000幅不同场景的高清图像,包括具有不同退化类型的低分辨率图像,其中有800张训练图像,100张验证图像,100张测试图像。Filckr2K数据集包含2 650张图像,包括人物、动物以及风景等。测试集采用Set5、Set14,BSD100以及Urban100,包含多种场景,常用于图像超分辨率重建的性能测试。Set5、Set14是常见的经典数据集,分别包含5张和10张动植物图像;BSD100包含100张不同场景的测试图像;Urban100包含100张图像,具有丰富的纹理。
4.2 评价指标
本文除了选取峰值信噪比(Peak Signal to Noise Ratio,PSNR)和结构相似性(Structural Similarity,SSIM)作为图像的客观评价指标外,还采用学习感知图像相似度(Learned Perceptual Image Patch Similarity,LPIPS)[33],用以衡量图像深度特征的相似性。
PSNR指的是单个图像接收到的最大信号值和噪声值之间的比值,可作为衡量图像质量的一个评价参数。PSNR表示重建图像的噪声失真强度,PSNR的值越大,则重建图像失真越小,其图像质量越好。SSIM是用来衡量两张图像在亮度、结构和对比度上相似性的定量指标,其取值范围为[0,1]。SSIM值越趋于1则重建图像效果越好。
Zhang等人[33]认为传统指标PSNR和SSIM并不能很好地表示重建图像的质量,并提出LPIPS,相比于传统方法PSNR和SSIM更能反映出由GAN所生成图像的感知优势。LPIPS的值越低表示两张图像越相似,反之,则差异越大。原始的高分辨率图像x与重建图像x0经过卷积神经网络的特征提取,对每一层输出的特征进行激活后归一化处理,记为再经过w层权重点乘并计算L2距离,最后求和取平均。公式如式(18)所示:
4.3 实验结果与分析
本节主要实验为卷积稀疏层迭代次数对实验结果的影响,以及本文算法和对比算法在4种测试集的2倍和4倍放大倍率进行实验对比,并做定性分析与定量分析,主要对比算法有Bicubic、SRGAN、EDSR和ESRGAN。
4.3.1 卷积稀疏层迭代数实验
为探究卷积稀疏模块的迭代层数对图像重建效果的影响,对不同的卷积稀疏层数在DIV2k验证集上进行放大因子为2倍和4倍的实验,并以PSNR值和SSIM值作为评价指标。如图6和图7所示,随着卷积字典层数k的增加,PSNR和SSIM值呈现先增大后减小的趋势,并在卷积字典层数k=12时达到最大值。其原因为迭代次数增加时,卷积稀疏层所提取图像的有用信息增多。在卷积稀疏层数k=12时,所提取的信息趋于饱和同时重建性能的提升也在逐渐变缓;而在迭代次数k>12时,随着迭代次数k的增加,网络加深,所提取图像的有效信息难以进行远距离传播,同时训练难度加大,导致整体性能下降。经综合考虑,后续与其他算法的对比实验采用的卷积字典层迭代次数均为12。

图6 不同迭代次数的PSNR结果Fig.6 PSNR results for different number of iterations
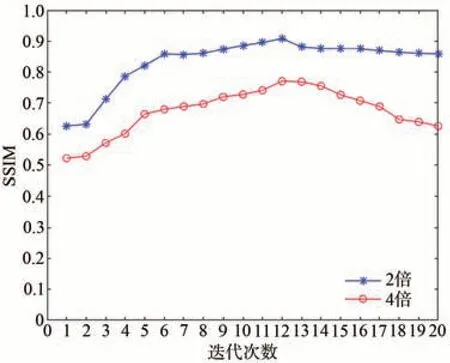
图7 不同迭代次数的SSIM结果Fig.7 SSIM results for different number of iterations
4.3.2 定量比较结果
表1和表2分别为不同模型在4类数据集的PSNR、SSIM和LPIPS值对比,所得结果均为在测试集上重复5次实验所得的平均值,加粗数据表示最好的结果。由表1可得,在2倍超分辨率实验中,本文所提模型在Set5测试集上的PSNR指标略低于ESRGAN模型0.155 8 dB;而在其他3个测试集上,本文所提模型的PSNR均获得最好的效果,比ESRGAN模型分别提升了0.595 2,0.315 3,0.932 5 dB。在4个测试集上,本文所提模型的SSIM值均得到最好的效果,与ESRGAN相比,分别提升了0.006 0,0.018 5,0.022 9,0.052 8。由表2可知,在4倍超分辨率实验中,本文所提模型在4个测试集上的PSNR和SSIM值均获得最优结果,与ESRGAN模型相比,PSNR值提升了0.843 1,0.946 6,1.083 2,1.062 0 dB,SSIM值提升了0.009 4,0.046 3,0.032 0,0.001 3。同时,在2倍和4倍的超分辨率实验中,本文算法在LPIPS上均获得最优的结果,相比ESRGAN的平均LPIPS值分别提升了0.021 0,0.010 9。上述定量实验结果表明,所提方法在客观指标上优于对比算法,且重建图像质量更好。
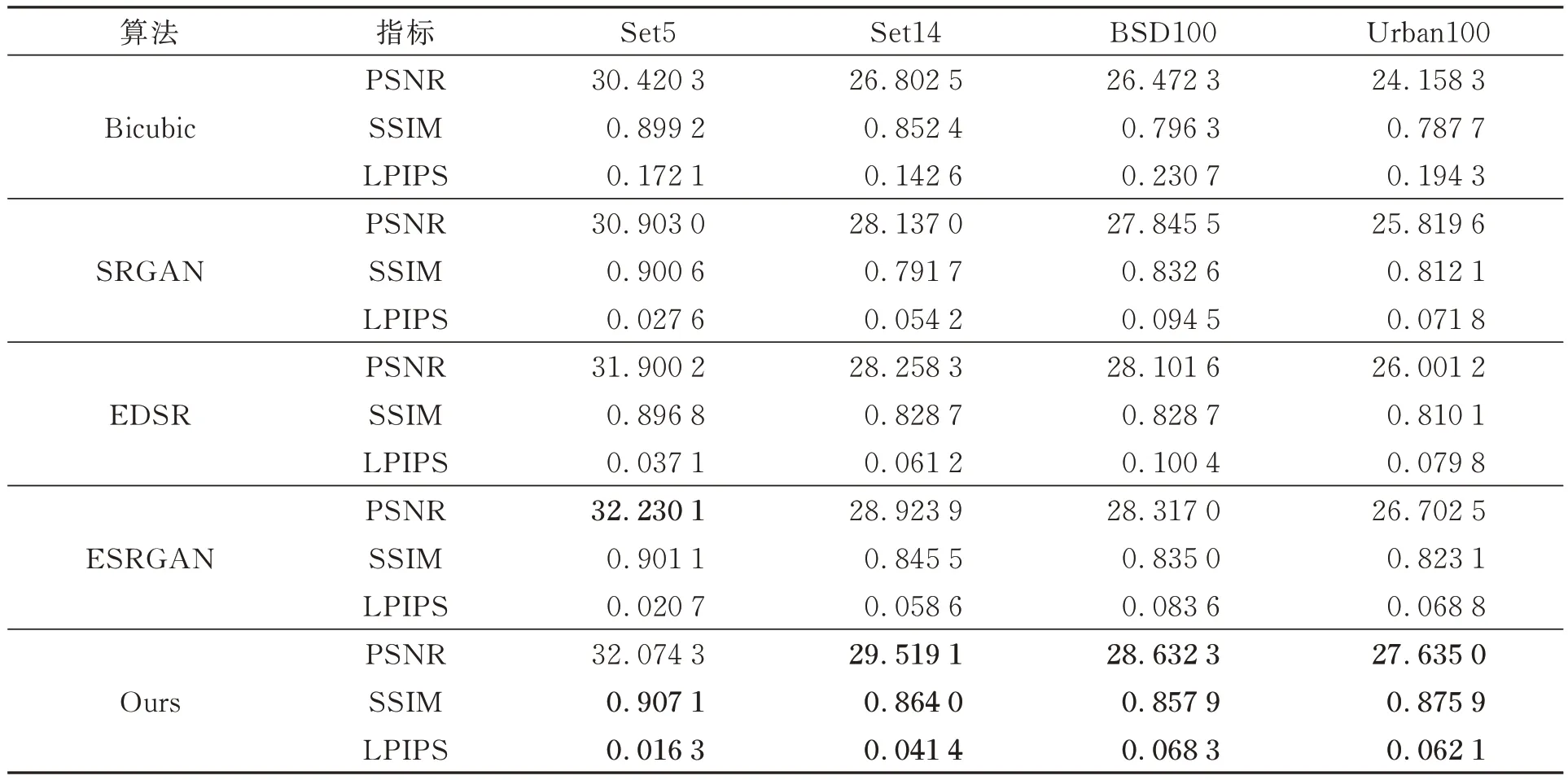
表1 各算法在2倍放大时的平均PSNR、SSIM和LPIPS值Tab.1 Average PSNR, SSIM and LPIPS values for each algorithm for ×2 magnification
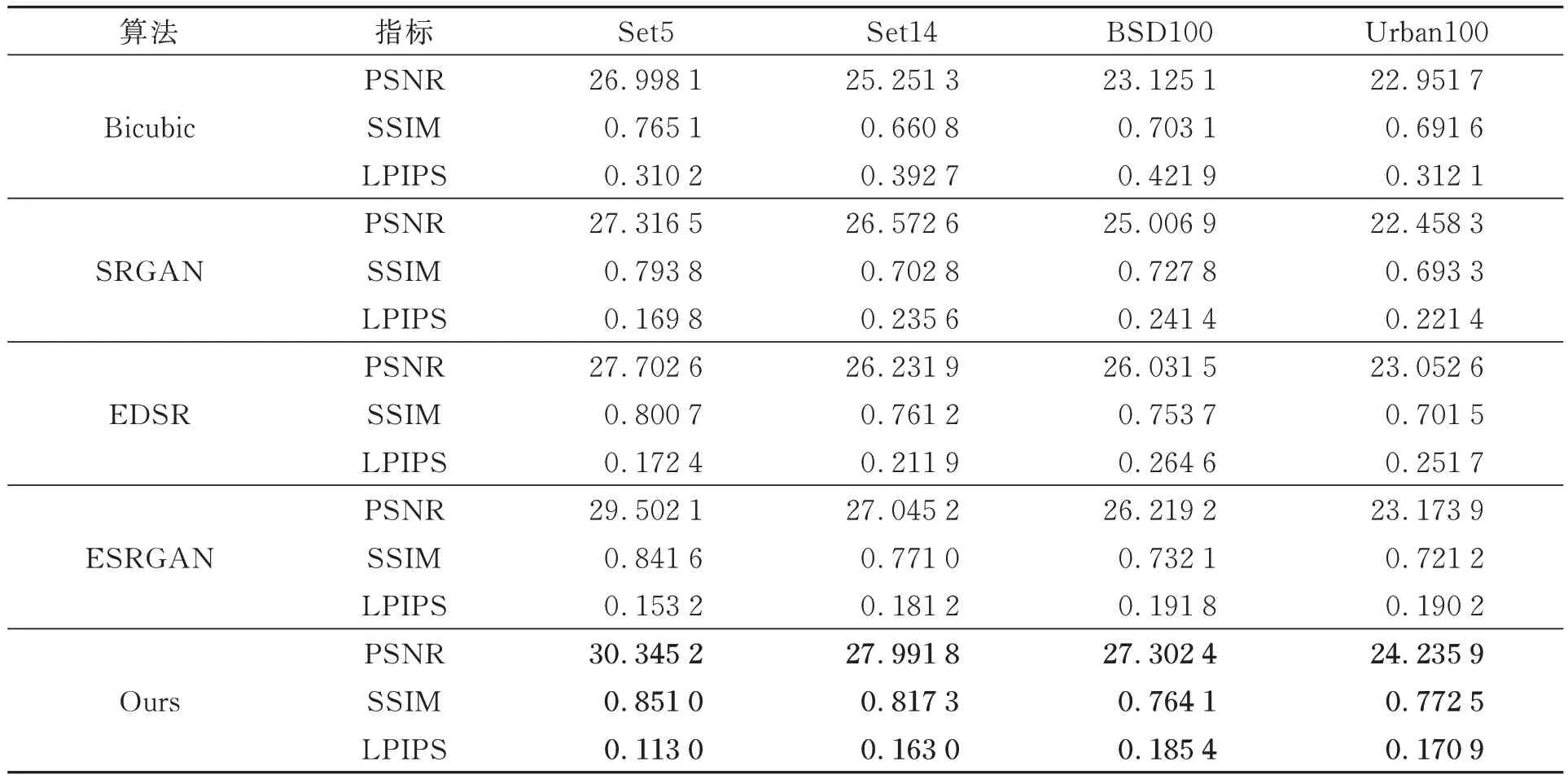
表2 各算法在4倍放大时的平均PSNR,SSIM和LPIPS值Tab.2 Average PSNR, SSIM and LPIPS values for each algorithm for ×4 magnification
4.3.3 定性比较结果
为了更直观地对比和验证本文算法与其他算法在主观视觉上的差异,如图8和图9所示,在4个测试集中选取6张图像,分别展示了各对比模型在测试集中的部分图像的2倍和4倍超分辨率重建的效果,图像左下角方框内的图像为局部区域放大图。

图9 各算法的4倍重建图像重建结果。(a)真实的高分辨率图像;(b) Bicubic; (c) SRGAN; (d) EDSR; (e) ESRGAN;(f)本文算法。Fig.9 4×super-resolution image reconstruction results of each algorithm.(a) High-resolution original images; (b) Bicubic;(c) SRGAN; (d) EDSR; (e) ESRGAN; (f) Ours.
结合图8和图9可以看出,由于Bicubic算法没有利用图像的先验信息,只是通过增加像素点,缺乏泛化性,导致重建的图像整体失真严重,不能清楚地观察到细节信息,且在4倍放大倍率时模糊程度加深。SRGAN算法相比Bicubic有较大的提升,但在细节信息的恢复上仍存在噪声,如图9(c)中,Image 4和Image 6显示SRGAN生成图像存在伪影和边缘结构信息模糊的现象。在EDSR网络框架中去除了归一化网络层同时添加了残差结构,重建图像在细节纹理上有着较好的视觉效果,但与本文算法相比,重建图像的轮廓不够锐利,如图8(d)中椅子的纹理和黑色的线条不够清晰,女子头巾的黑色条纹较为模糊。而本文算法的重建图像相对其他算法,整体清晰且边缘锐利。ESRGAN算法恢复的效果质量整体上都较为清晰,但在细节恢复部分伴随着噪点和结构不清晰,如图8(e)可以看到Image 1石像的细节部分存在噪点;图9(e)的Image 6中生成的树枝结构杂乱,纹理细节不清晰,并伴随大量的伪影和噪声。而本文算法生成的树枝结构清晰,更接近原高分辨率图像的树枝结构。本文所提算法的重建图像与其他对比算法的重建图像相比,获得了更丰富的纹理信息和清晰的边缘特征,视觉效果更好,更接近原始图像,如在图9的Imgae 4中,EDSR算法和本文算法能够恢复阳台中间的栏杆。其他算法生成图像的细节部分几乎丢失。在墙沿的恢复上,本文算法相比于EDSR具有更好的细节。实验结果图显示,由于卷积稀疏编码可以很好地保留图像的高频结构信息,本文算法能够在恢复图像细节时保证图像清晰度,也避免了重建过程中产生的噪声和伪影,取得良好的主观视觉效果,相比其他对比算法有着优异的表现。
5 结 论
本文提出了一种基于卷积稀疏编码和生成对抗网络的超分辨率重建模型。利用卷积网络来实现稀疏编码并获取图像稀疏表示,然后将得到的稀疏表示经过重建模块得到重建的高分辨率图像,使该模型可以将图像作为网络的输入,避免了传统算法的复杂的图像处理以及数据重建的过程,同时也具有稀疏字典学习捕获图像的高频结构信息的优点,解决高频信息缺失和存在噪点的问题。利用鉴别器对生成的重建图像进行鉴别,减少重建图像的涂抹感,使重建图像有更好的视觉效果。所提的模型表明,传统稀疏编码模型所蕴含的领域知识对深度学习的网络设计依旧具有重要的指导意义,所提方法在4个数据集上的平均PSNR提升约0.702 8 dB,平均SSIM提升约0.047,平均LPIPS提升了0.016,在客观评价和主观视觉上获得了良好的效果。

