经济增长率偏好影响下的经济增长①

张 荣, 张 华, 任庆忠

(1. 重庆大学经济与工商管理学院, 重庆 400030; 2. 重庆工商大学会计学院, 重庆 400067; 3. 重庆工商大学管理科学与工程学院, 重庆 400067; 4. 重庆理工大学经济金融学院, 重庆 401135)

0 引 言

在经济发展的不同阶段,许多国家都明确地或隐含地制定预期经济增长目标,这在一定程度上反映了人们对经济增长率的偏好.比如,我国自1953年开始,每隔五年制定一个国民经济和社会发展五年计划,设立一些主要的经济和社会发展目标,从“七五”规划到“十三五”规划,这期间设定的经济增长率目标大致在7%左右.国内外有许多文献从不同的角度分析经济增长率偏好及其影响.较早的文献Tobin[1]指出,无论是在美国还是在其他国家,无论是发达国家还是欠发达国家,无论是中央控制经济体还是分散经济体,经济增长目标在政府政策目标层次中均占据很高的地位.经济增长不仅是各个国家追求的目标,它已成为国际性的目标.中国最近四十年来的经济增长率举世瞩目,有众多文献对我国经济增长问题进行过深入的分析,其中也有部分文献分析了经济增长目标及其潜在影响.徐现祥和刘毓芸[2]从经济增长目标管理的角度分析了它对经济增长的影响.他们指出,经济增长是宏观经济管理的目标之一,自1950年至今,至少有49个包括发达和发展中国家在内的众多经济体一直或曾经定期公布经济增长目标.最近也有许多文献研究了地方政府经济增长目标及其影响.在这些文献中,有不少文献运用我国230个地级市经济增长目标相关数据进行了实证分析[3-7].

本文的主要目的不是去讨论这种经济增长目标是否可以如期实现,而是讨论这种普遍存在的“对经济增长率的偏好”给经济增长带来的潜在影响.在传统的新古典经济增长模型中,家庭或消费者的效用函数通常被假定为仅仅与消费水平有关[8-10].然而,当人们普遍地表现出对经济增长率存在偏好时,如果仍然采用上述只依赖于消费水平的效用函数,那么该传统的模型就有可能遗漏某些重要的性质.为了反映上述经济增长率偏好对效用函数所带来的影响,本文在传统新古典模型框架下,假定效用函数不仅包含了因消费而产生的效用,同时还包含了因经济增长率偏好而带来的额外效用,从理论上分析这种因喜欢高增长率的偏好给最优消费、最优投资以及消费者总效用等所带来的潜在影响.

除了以RCK模型为代表的新古典增长模型之外,另一类重要的经济增长模型是内生经济增长模型.内生经济增长模型在很大程度上是去寻找克服边际报酬递减的机制,进而解释经济持续增长的内在动力,其中很有影响的模型包括Romer[11, 12]的水平创新模型(产品种类的增加),以及Aghion和Howitt[13]的垂直创新模型(产品质量的提升).这两类模型都认为因获取短暂垄断利润而进行的不断创新是经济持续增长的源泉,它们从不同角度对Schumpeter[14]“创造性破坏(creative destruction)”的思想进行了简明的诠释[15].从后面的分析中可以看出,经济增长率偏好也可以纳入这类典型的内生经济增长框架来进行分析.但限于篇幅,本文的研究将主要集中在新古典经济增长模型框架下进行分析.

经济增长问题是一个跨期优化问题,人们当前的消费决策会影响资本形成,进而影响未来的产出水平.在以往关于经济增长的研究中,许多文献主要集中于生产函数或生产要素一侧的研究,而侧重于效用函数一侧的研究相对较少[16, 17].本文对带有经济增长率偏好的经济增长模型的分析,不仅有助于从理论上发现和理解这种“普遍存在的经济增长率偏好”对经济所带来的潜在利弊,同时也有助于人们在现实中形成比较理性的经济增长率偏好,制定更为合理的经济增长目标.

研究表明,经济增长率偏好对最优消费、最优资本以及消费者总效用等的影响结果,与直观想象是存在差异的.比如,它对稳态消费的影响并不像预期那样是单调递增的,适度的经济增长率偏好才可以使得稳态消费超过传统新古典增长模型中的稳态消费;如果初始资本存量已经比较高,那么经济增长率偏好的上升反而会使得一生的总效用降低;随着经济增长率偏好的增强,经济收敛速度在稳态附近将变得更低.同时,经济增长率偏好的引入,也会改变传统新古典增长模型的部分性质,比如时间偏好等参数对稳态资本存量的影响也不再是单调递增或递减.本文的研究结果表明,政府过度地追求高经济增长率或不顾发展阶段一味地偏好经济增长率,都可能会带来产能过剩、稳态消费与总效用降低等负面影响.另外,从本文的分析中还可看出,通过诸如“晋升锦标赛”等反映经济增长率偏好的激励方式来促进经济增长[18, 19],虽然可能起到一定作用,但其作用可能十分有限.

1 模型描述与求解

1.1 模型描述

虽然有许多文献研究经济增长偏好及其影响,但至今没有发现将经济增长率直接纳入效用函数,以从理论上分析经济增长率偏好对经济增长的潜在影响.从一定程度上说,Chakravarty 和Manne[20]构造的效用函数的思路与本文构造效用函数的思路具有一定的相似性.该文认为,个人或家庭不仅关心消费的绝对水平,还关心消费水平的变化或增长率.他们在论文的一开始就通过简单的例子解释了“为何消费的增长率会带来效用”,然后在Ramsey[8]模型中将消费的增长率直接引入到效用函数.虽然经济增长与消费增长是两个不同的概念,但在常见的RCK新古典以及内生经济增长的框架下[8-13],这两者具有紧密联系,因此将经济增长率放入效用函数可得到类似解释.但与Chakravarty和Manne不同的是,本文的效用函数不仅包括了经济增长率带来的效用,同时还包括了通常意义下消费带来的效用.应该说,本文的效用函数更具有一般性,因为当α=0时(其含义见随后的解释),本文的模型即退化为传统的新古典经济增长模型,而Chakravarty和Manne的效用函数则不具有这一性质.

为了使效用函数既能反映消费对它的影响,又能反映经济增长率偏好对它的影响,本文假定模型如下(1)不存在外部性等条件时,完全竞争的一般均衡结果与社会计划者(social planner)的最优结果是一致的,可参见Romer[22]和Acemoglu[23],因此,也可以认为该目标函数是社会计划者的目标函数,而根据它所得到的最优消费、资本等路径与一般均衡所得的结果一致.

(1)

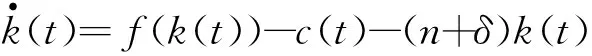
k(0)=k0

(2)

这样,本文的问题就变化为一个标准的最优控制问题,即消费者选择最优消费路径c(t),在资本的状态方程约束下,使得一生的效用达到最大.

1.2 模型求解

上述问题可以运用最优控制理论来求解[21].首先,由经济增长率的含义、人均产出的表达式以及资本的积累方程(2),可以将经济增长率表示为

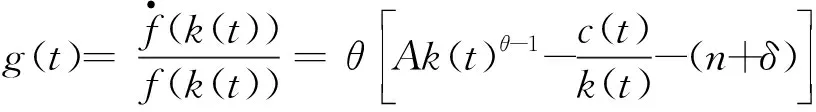
(3)

构造如下Hamilton函数

λ(t)[Ak(t)θ-c(t)-(n+δ)k(t)]

(4)

其中λ(t)为协态变量,它表示t时刻资本存量的影子价格.由一阶条件可得

(5)

易见,当α=0时,λ(t)=1/c(t),该等式的左侧表示因放弃一单位当前消费在未来得到的好处,而右侧表示因放弃一单位当前消费的效用损失.因此,最优化行为要求减少单位消费所带来的边际好处与边际损失相等,这也对应于传统新古典经济增长模型中的情形.但当α>0时,除了当前的边际效用损失由α=0时对应的1/c(t)降至(1-α)/c(t)之外,同时还会在此基础上减少αθ/k(t),这意味着资本的影子价格降低,从而会影响当前消费与投资.

由Hamilton函数可得到协态方程为

(6)

横截条件为

(7)

将式(5)两边同时对时间t求导得

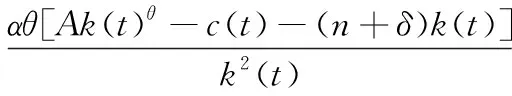
(8)

由式(2)、式(5)、式(6)和式(8)可得

(9)

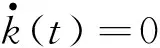
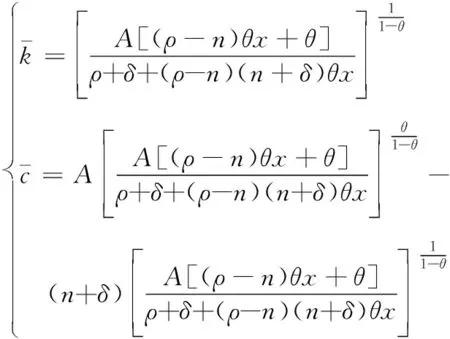
(10)

由式(10)易见,当x=0时,该结果正是传统新古典增长模型的最优稳态均衡.

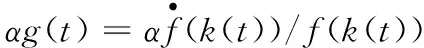
另外,据了解,在同时满足效用函数为CRRA效用函数以及生产函数为线性生产函数的条件下,这类经济增长问题(也包括特定的随机情形)具有显式解,而除此之外的情形很难具有显式解(4)Obstfeld M. Dynamic optimization in continuous-time economic models (a guide for the perplexed). Manuscript, University of California at Berkeley, 1992.,因此相关的分析也变得十分复杂和困难.Zou[27]使用的效用函数为u(c)+v(k),不难看出它对c和k的交叉弹性为零,Zou在定量分析中所使用的效用函数和生产函数也大致具有Obstfeld的结构,这使得其分析不是很复杂.本文模型中的瞬时效用函数中的c和k在本质上是不能分离的,因此效用对c和k的交叉弹性是不为零的,这一数学上看似细微的差异却可能给这类问题的分析带来不小的困难[17, 28],这一点也可以从与Zou的对比中看出.另一方面,本文的分析也从一个侧面反映了Kurz[24]当初的预测存在一定瑕疵.比如,Kurz猜测财富效应影响下的经济增长在一定条件下存在多重均衡,而Bose[29]指出,即使在比较一般的条件下,Kurz模型的多重均衡也不存在,本文模型中均衡的唯一性也反映了这一点.

1.3 主要性质

本节主要进行比较静态分析,定量分析各个参数对均衡消费以及均衡资本等重要变量的影响.

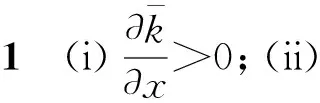
证明由式(10)可知

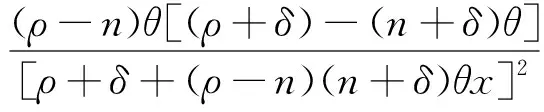
(11)

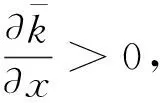
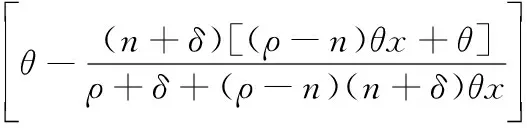
(12)

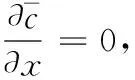
改革开放以来,中国经济保持了30多年的高速增长,取得了举世瞩目的成就.据中国国家统计局的数据显示,中国的国内生产总值(GDP)在1980年—1997年和1998年—2014年间年平均增长率分别为10.11%和9.46%.从对中国经济增长的解释来看,除了从传统的影响因素(比如技术创新、人力资本、自然资源等)来对其进行分析外,也有研究者立足于我国特定的政治制度背景,基于“晋升锦标赛”机制来进行分析,即官员在任期内所辖地区经济表现越好,晋升概率就越高.但从命题1可以看出,在新古典框架下,由于资本边际产出递减规律的影响,经济最终会趋于稳态,因此通过这种反映经济增长率偏好的激励方式来促进经济增长,可能仅在过渡过程中会起到一定作用.从长远来看,这种激励方式对稳态消费水平虽然也存在一定影响(6)根据命题1,稳态消费水平在x∈(0,xgold)时确实随经济增长率偏好x的增加而增加.,但是,从后面的实际仿真来看,其作用可能十分有限.

在传统新古典经济增长模型中,由于时间偏好ρ的引入,人们更倾向于当前消费,这使得人们的稳态消费会低于黄金法则对应的消费水平,这也是储蓄率内生的RCK模型与储蓄率外生的Solow模型在最优解性质方面的一个重要差异.而在本文的模型中,不难证明,当x=xgold时,消费水平刚好能达到黄金法则对应的消费水平.这一结论看似与传统结论相矛盾,但实际上可以通过这样的方式来解释:时间偏好系数的引入虽然使得人们有提前消费的倾向,但经济增长率偏好的引入会激励人们更倾向于资本积累,从而有抑制当前消费的作用,当后者力量比较大时,就有可能使人们的消费达到黄金法则对应的水平.

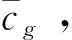
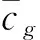
(13)

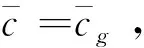
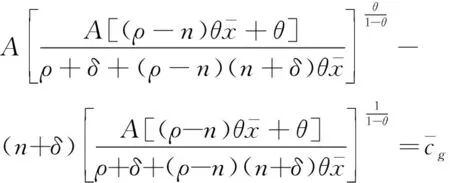
(14)

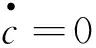
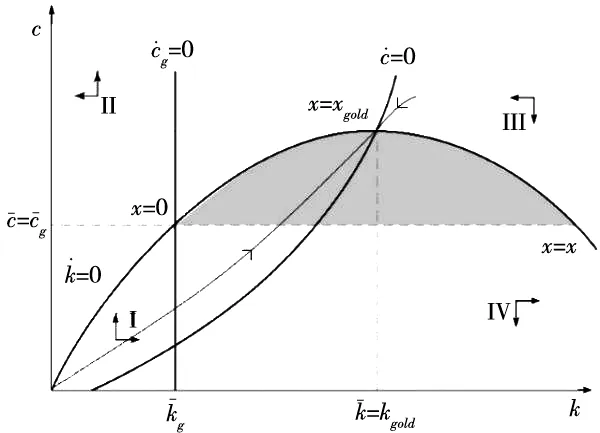
图1 新旧模型的相平面对比分析Fig.1 Phase-plane analysis of the old and new models

另外,命题2还表明,虽然本文的稳态资本可能高于黄金资本存量,但此处并不存在Solow模型中的动态无效性(9)即:如果增加当前消费,不仅不会减少未来的消费,却反而可以使得未来的消费提高,产生这一结果的主要原因是Solow模型中没有考虑家庭的优化行为.(dynamic inefficiency).从直观上说,人们对经济增长率的偏好,在本模型中会间接地传递到对资本存量的偏好.因此,资本看似非消费品,但其作用在一定程度上与消费相似.粗略地说,此时有两种力量会影响效用:消费与资本.过高的资本(高于黄金水平的资本)会使得均衡消费下降,从而使得效用有下降的趋势;但资本水平上升会使得效用又具有上升的趋势.此处效用一增一减这两种力量均是家庭动态优化的结果,因此不存在动态无效性.

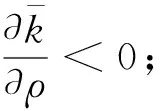
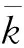
(15)

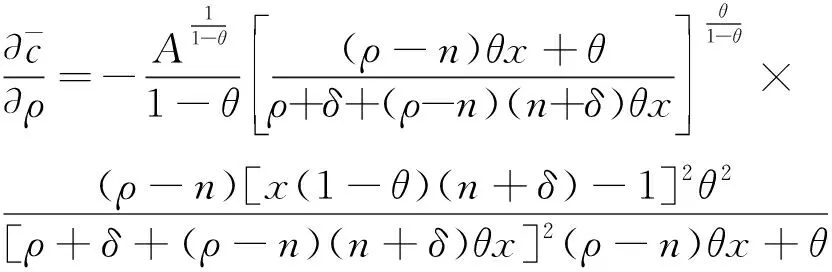
(16)

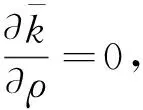
按常见的假定,在不考虑人力资本的条件下,资本的产出弹性θ≈1/3,人口增长率n≈1%,折旧率δ≈10%,那么xgold≈13.64.欲使得相对偏好x>xgold,由相对偏好的定义x=α/(1-α),那么要求α>0.93;如果此处的k还包括了人力资本,那么θ的取值一般在2/3左右[31],这就需要α>0.96.不难看出,无论是否包含人力资本,如果需要满足x>xgold,那么α的取值都会很大,而很高的α取值表示人们对经济增长率极其偏好,虽然理论上存在这种比较极端偏好的可能性,但在真实的经济中,出现这种情况的可能性应当是很低的.这意味着,在很多情况下,仍然是越有耐心的民族可能最终会获得更高的稳态资本存量和稳态消费.

1.4 θ=1的情形

为了进一步研究该模型的定量性质,在上面引入经济增长率偏好的框架下,研究资本边际产出不变的情形,亦即当θ=1时(11)Obstfeld M. Dynamic optimization in continuous-time economic models (a guide for the perplexed). Manuscript, University of California at Berkeley, 1992.,在通常的AK模型中纳入经济增长率偏好.

对于该特殊情形,将θ=1代入到式(9)并经过适当调整可得

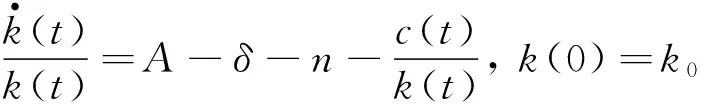
(17)

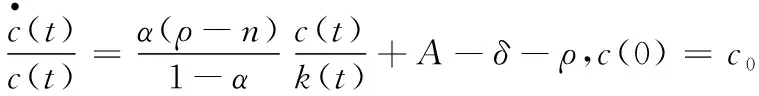
(18)

其中参数c0为待定的初始最优消费量.

命题4最优消费路径c*(t)与资本路径k*(t)的增长率相等,其大小为g*=A-η-n-δ,k*(t)与c*(t)的最优增长路径分别为

(19)

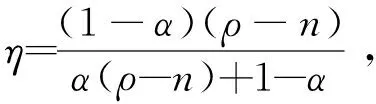
(20)

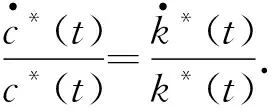
(21)

于是

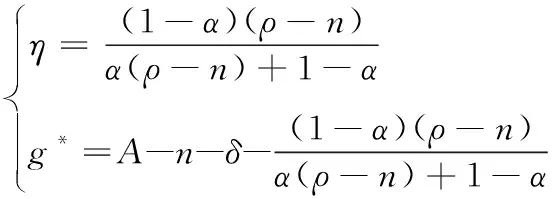
(22)

=0

(23)

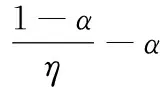
由式(22)可知,最优经济增长率由技术水平、人口增长率、资本折旧率、时间偏好以及经济增长率偏好等因素决定.根据传统新古典经济增长模型,如果两国在技术水平、人口增长率、资本折旧率、时间偏好等方面都相当,那么两国的最优经济增长路径也基本一致,但在本文的框架下,其最优增长路径也可能因对经济增长率的偏好而不同,这为某些条件相似的国家或地区具有不同经济增长率的现象提供了一种可供选择的解释.

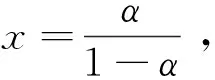
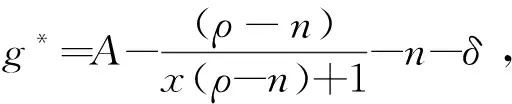
(24)

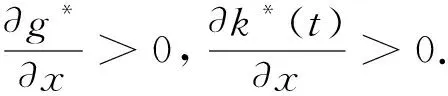
命题5表明,经济增长率偏好程度越强,最优经济增长率g*则越高,这一结论也比较符合直观的理解.在命题1中,人们越偏好经济增长率,将越注重资本积累而抑制当前消费,从而表现出国家储蓄率越高,而由于此处当θ=1时,资本的边际产出不变,因此经济增长率g也会随储蓄率的上升而上升,资本存量k*(t)也会随之增加.

(25)

当α→1时,式(25)的极限存在,通过简单计算可得

(26)

从式(26)可看出,当α→1,即消费者几乎仅仅偏好经济增长率时,效用值与人均初始资本存量k0是无关的.这是因为此时几乎不关心消费,而仅仅关心经济增长率,当然人均初始资本存量k0的高低也就显得无足轻重了.这一结果虽然可能不太现实,但在理论上有助于理解初始资本存量对经济增长率偏好作用的潜在影响.而且由式(26)容易看出技术水平参数A、折旧率δ、时间偏好ρ等参数对最优总效用水平的定量影响,此处不再赘述.

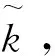
证明当α=0时,

(27)

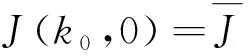
(28)

可得

(29)

2 收敛性质分析

为了方便分析稳态均衡点式(10)附近的收敛性质,可首先将k(t)和c(t)的动态系统式(9)进行对数线性化[31].这样微分方程组(9)可被改写成(13)在不发生混淆的情况下,以下将省略时间t.

(30)

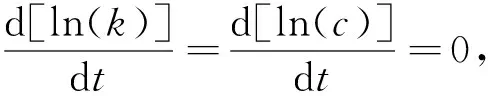
(31)

将式(30)在稳态附近进行线性化,并注意到式(31),可得

(32)

其中

(33)

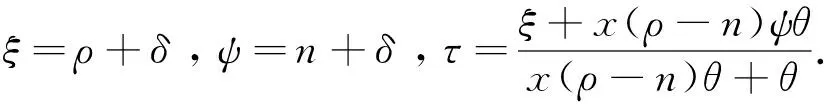
(34)

可计算其特征值ε.该条件相当于关于ε的二次方程式

ε2-(a+d)ε+ad-bc

(35)

该方程具有两个解

(36)

其中

(37)

因为0<θ<1,ρ>n,τ>0,所以ad-bc<0,即式(36)存在两个异号的实根,其中,正根记为ε1,负根记为ε2.这也印证了相平面分析(见图1)中关于均衡解是鞍点解的结论.令β=-ε2,则对数线性化方程的解可表示为

(38)

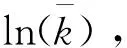
(39)

结合φ1=0、式(38)和式(39),可得

(40)

易见,α的大小反映了该经济在稳态点附近的收敛速度.注意到

(41)

根据式(41)可得

(42)

又因为

(43)

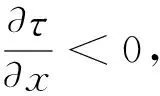
命题7随着经济增长率偏好的提高,稳态附近的收敛速度将降低.

命题7看似与直觉违背,因为人们越偏好经济增长率,就会越抑制当前消费,资本积累速度就越快,因此均衡路径上的消费与资本的收敛速度就应当越快.由于相关表达式的复杂性,因此难以从理论上对此给出严格的证明,但从大量的数值仿真可以看出,当初始资本存量远离稳态时,最优路径在动态(过渡)过程的收敛速度确实随对经济增长率偏好的上升而上升(见第3节中的图4).

但是,当资本接近稳态时,理性行为应当是让经济增长速度不宜过快,这样才可能在较长时间内保持一定的经济增长率,而经济增长率的边际效用为正,从而总效用才可能提高,即命题7所预示的结论.均衡路径在稳态附近的行为可用吉尼斯世界纪录保持者的行为来进行类似分析,如果吉尼斯纪录的保持者每次打破之前纪录能够带来好处的话,那么他的理性决策应当是每次仅仅超过前一次纪录很小的幅度即可,这样才能在未来有多次打破纪录的机会,从而带来更多的好处.相反,如果一下子达到自己的极限,超过前一纪录很高的幅度,那就可能没有机会打破自己的纪录,因而也会失去潜在好处.

上述分析也说明,经济增长文献中用线性系统去近似分析非线性系统在稳态附近的性质,可能具有较大的局限性.比如,本文中经济增长率偏好参数α对过渡过程收敛速度的作用与其对稳态附近收敛速度的作用甚至是相反的.因此,许多经典文献中基于稳态附近的收敛速度来测算经济达到某一水平(比如常见的离稳态一半距离)所需要的时间,可能存在比较高的误差[22, 31].

当经济还处于相对较低的阶段时,我国在一定程度上采取了反映经济增长率偏好的激励机制,这有助于保持较高的经济增长率,这与上述离稳态较远的过渡过程相对应,因此是理性的选择.而经过三十多年的持续增长,我国的人均产出等得到大幅度提高,如果此时仍然采取反映经济增长率偏好的激励机制,那么根据命题7的结论,该激励机制不仅不会促进经济增长,反而可能使得经济增长率减缓.虽然难以判断当前经济水平离稳态究竟有多远,但政府适度降低对经济增长率的偏好,可能也是理性的选择.这一结果类似于张军等[32]关于社会福利与环保力度的结论.

3 模型仿真分析

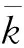
3.1 经济增长率偏好对稳态均衡的影响

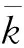
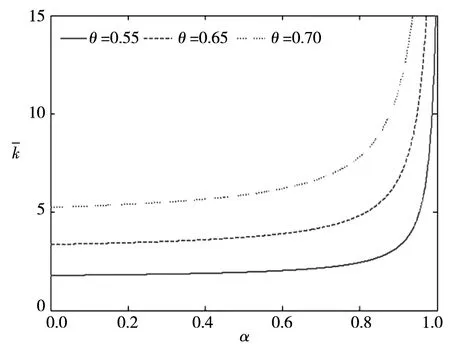
(a)

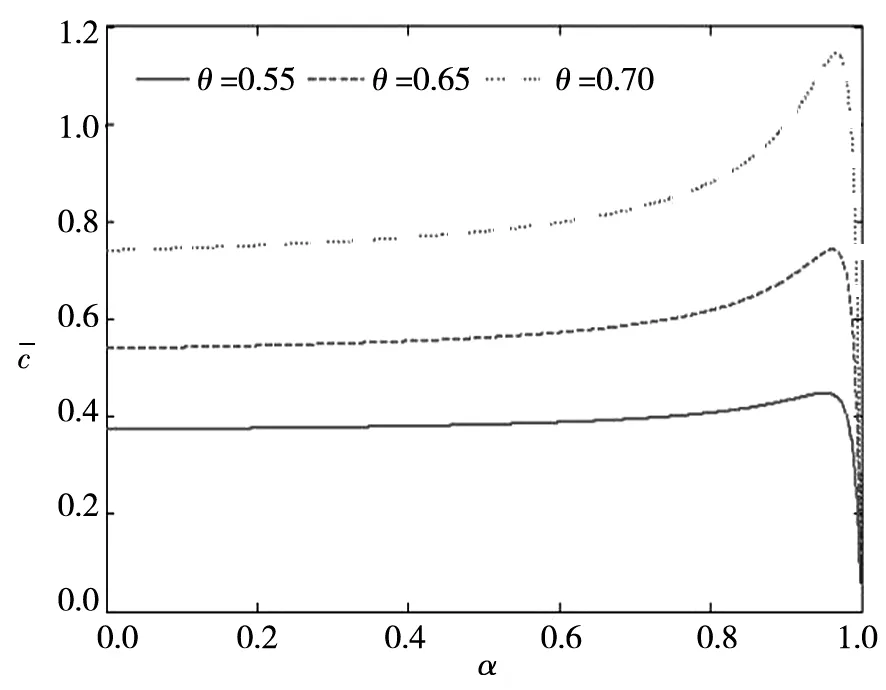
(b)图2 经济增长率偏好对稳态均衡的影响Fig.2 Effect of economic growth rate preference on steady-state equilibrium

3.2 经济增长率偏好对稳态附近收敛速度与收敛时间的影响

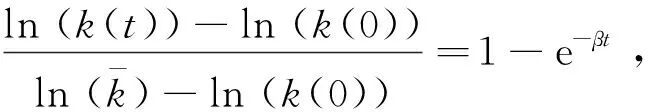
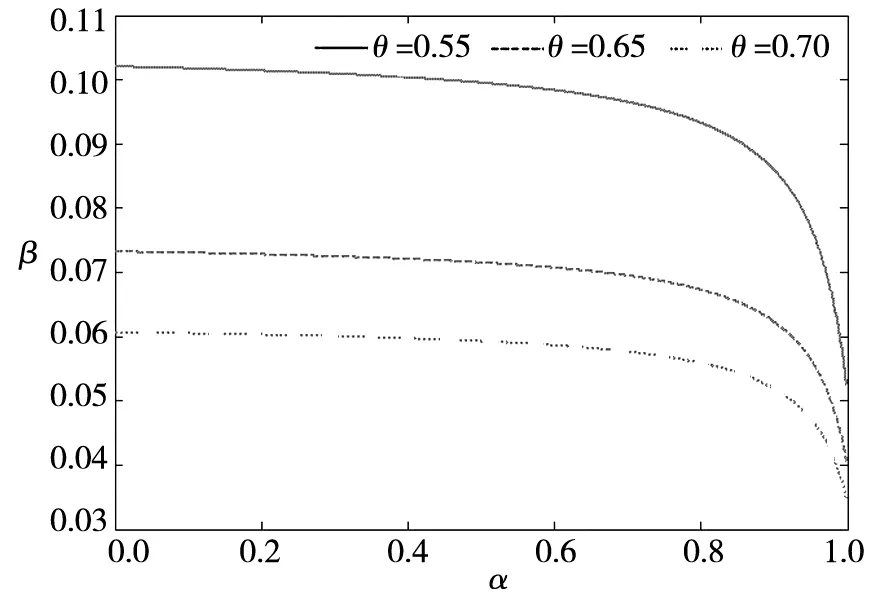
(a)

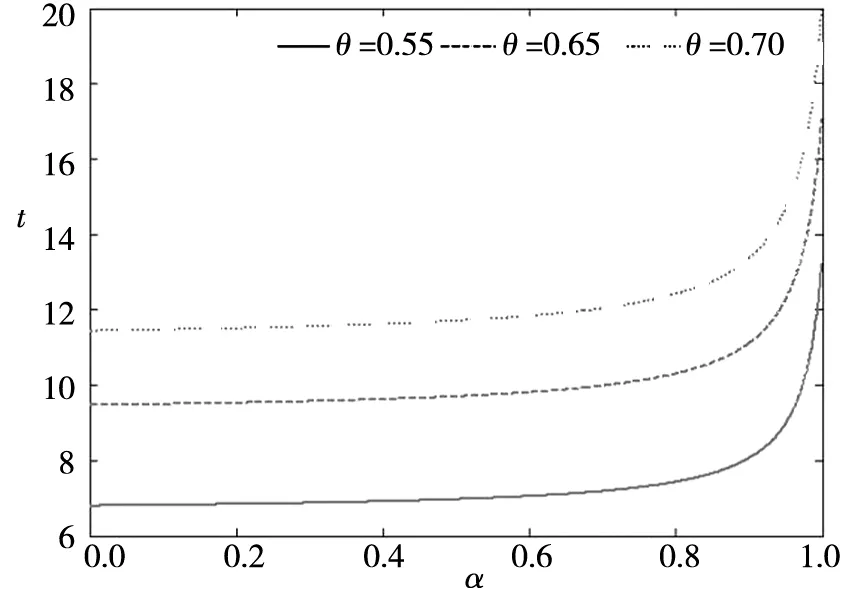
(b)图3 经济增长率偏好对稳态附近收敛速度与收敛时间的影响Fig.3 Effect of economic growth rate preference on convergence speed and converge time near the steady state

图3(a)与图3(b)分别表示经济增长偏好对稳态附近收敛速度与收敛时间的影响.可以看出,当经济增长率偏好α大约在0～0.7范围内时,收敛速度与收敛到一半的时间并无明显变化,而当α大约在0.7～1的范围内时变化,收敛速度与收敛时间的变化较为明显.这一数值结果在一定程度上也与图2所示的数值结果相互印证.

3.3 经济增长率偏好对过渡过程收敛速度的影响

此处相关参数的取值与前面的基本一致,即δ=0.11,ρ=0.07,n=0.005,θ=0.7,A=0.42.为了分析不同经济增长率偏好对过渡过程收敛速度的影响,α分别取α1=0.93与α2=0.96.据汇丰银行中国资本存量的估算显示,2010年中国资本存量约为93万亿元,再结合当时我国人口总量可测算出中国人均资本存量约为7万元,因此取初始资本存量k0=7.

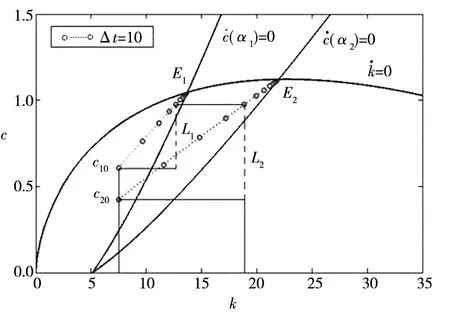
图4 经济增长率偏好对过渡过程收敛速度的影响Fig.4 Effect of economic growth rate preference on the convergence rate of transition process

4 实证检验(15)本节只是简要的实证分析,在样本容量大小、控制变量选取等方面显得比较松散,更仔细的分析无疑将是未来研究一个很有价值的话题.

前面将经济增长率偏好纳入传统新古典经济增长模型,获得了最优稳态资本存量与消费的显式表达式,主要从理论上分析了经济增长率偏好对均衡资本、均衡消费及效用水平的影响,同时也给出了一定的数值仿真,本节将对经济增长偏好对资本、消费的影响进行初步的实证分析.经济增长偏好这一指标通常难以直接量化,但各省区市政府工作报告中的经济增长目标可以用来间接反映经济增长偏好(16)感谢匿名审稿人的这一建议.,这在徐现祥等[2]、余永泽等[3-5,7]、刘淑琳等[6]的相关文献中已有比较丰富的分析,相关实证分析也可能直接用于检验前面的某些理论结果.比如,徐现祥等[2]的研究结论“经济增长目标管理能够较显著地倒逼资本积累”,刘淑琳[6]等利用政府工作报告公布的经济增长目标数据,验证了经济增长目标驱动辖区投资增长的理论假说,这些实证结果与本文图2(a)表示的情形一致,即经济增长偏好有助于提高稳态资本水平(17)本文的理论分析主要针对的是经济处于稳态或稳态附近的情形,而我国经济增长在很长一段时期内仍将处于动态的过渡过程,因此即使这些实证从一定程度上支持了图2(a)所表示的理论结果,但理解它们时仍然需要注意区分稳态和过渡过程的某些性质差异..另外,图2(b)表示的情形也是本文重要的情形之一,它表示过度的经济增长偏好将可能降低稳态消费水平.为了检验这一理论结果,下面以2009年—2017年中国31个省区市为研究样本,对我国经济增长率偏好与消费之间的关系进行简要的实证分析.

4.1 变量选取与数据来源

1)被解释变量:居民消费支出(consumption),数据源于国家统计局.

2)解释变量:经济增长率偏好(preference).利用各省区市政府工作报告中的经济增长目标来表示经济增长偏好,数据来各自省区市政府网站上公布的相关年份政府工作报告.

3)控制变量:居民可支配收入(income).居民可支配收入是影响居民消费支出的主要因素,本文将它作为控制变量,数据源于国家统计局.需要说明的是,影响居民消费的因素众多,未来更详细的实证研究通常应将这些影响因素也纳入分析.为避免内生性问题,本文选用滞后一期的居民可支配收入作为控制变量.由于国家统计局在2013年之前尚未开展城乡一体化住户收支状况调查,而是对城市和农村分别调查,为保持数据口径一致性,对2013年之前各省数据,按照“城镇人口×城镇人均可支配收入+乡村人口×乡村人均纯收入”计算得到居民可支配收入.另外,为削弱异方差性,本文对可支配收入以及居民消费支出取自然对数.各变量的统计性描述如表1所示.

表1 变量统计性描述Table 1 Descriptive statistics of the variables

4.2 实证结果

随机效应模型认为随机扰动项与解释变量是不相关的,这个假定在现实中较难得到满足.为此,本文直接选择固定效应模型进行实证检验,构建的计量经济学模型具体如下

ηincomei,t-1+λt+γi+εi,t

(44)

其中consumptioni,t和preferencei,t分别表示省区市i在时期t的居民消费支出和经济增长率偏好,λt和γi分别表示时间固定效应和省份固定效应,incomei,t-1表示滞后一期的可支配收入,εi,t为随机扰动项.

模型参数估计结果具体如表2所示,由表2可得,经济增长率偏好水平项对居民消费支出具有显著的正向影响,而二次项则具有显著的负向影响,这说明经济增长率偏好对居民消费支出具有倒“U”型的影响.经济增长率偏好与居民消费支出的倒“U”关系,表明当经济增长率偏好低于门槛值时,经济增长率偏好的提升将促进居民消费支出,但当经济增长率偏好超过门槛值后,经济增长率偏好的进一步提升将抑制居民消费支出,该结论与图2(b)所表示的情形一致,这也说明本文所构建的理论模型能够较好地用于解释现实.

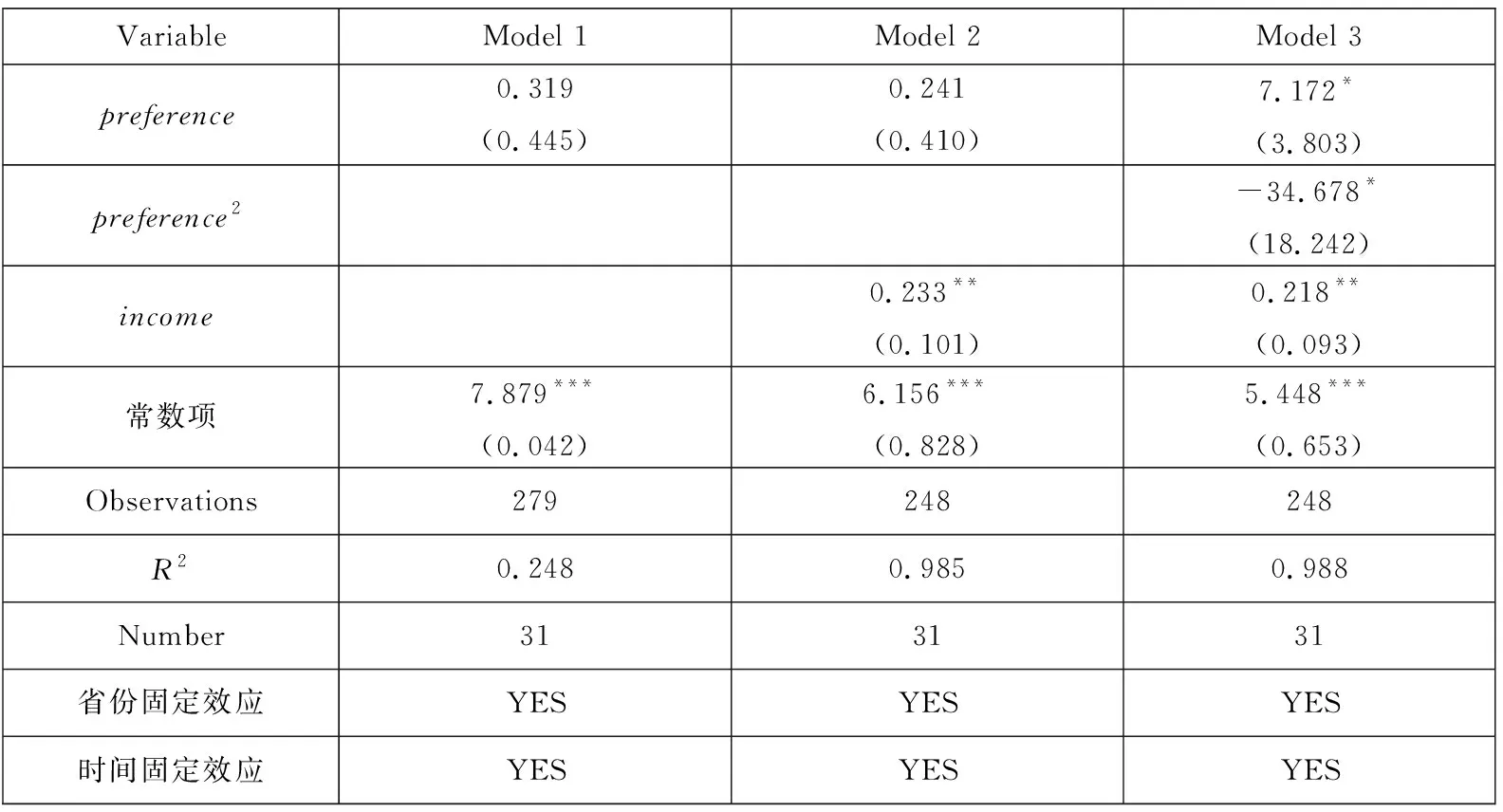
表2 回归结果Table 2 Regression results

5 结束语

为了分析经济增长率偏好对经济增长所带来的潜在影响,本文将人们对经济增长率的偏好纳入传统的新古典经济增长模型,并在此基础上分析了喜欢高增长率的偏好对经济均衡消费、均衡资本以及效用水平等带来的潜在影响.从研究结果来看,在经济发展相对较低的阶段适度地偏好经济增长率,不仅可使得稳态资本和稳态消费均提高,同时还可以提高总的效用水平;但是,过度地追求高经济增长率而不顾及经济所处的发展阶段,可能使得稳态消费水平反而会降低,同时消费者一生总的效用水平也可能降低.因此,一味地肯定或一味地否定政府对经济增长率的偏好,看来都是不妥当的.随着人们对经济增长率偏好的上升,经济在稳态附近的收敛速度将减缓.另外,政府想通过诸如“晋升锦标赛”等反映经济增长率偏好的激励方式来促进经济增长,从长期来看其作用可能十分有限.

回顾我国过去数十年的经济发展,当经济还处于相对较低的阶段时,我国在一定程度上采取了反映经济增长率偏好的激励机制,这不仅有利于提高居民稳态消费,同时还可以增加消费者的总效用,这正是本文模型所蕴含的最优策略;而经过三十多年的持续增长,我国的人均产出和人均资本存量已经得到了大幅度提高,某些行业已经出现比较严重的产能过剩,因此政府此时适度降低对经济增长率的偏好,也是明智之举.