矩形狭缝裂隙水流运动特征数值模拟研究

张帅领,张春艳,江承阳,杨亚东

(1.中国电建集团河南省电力勘测设计院有限公司,河南 郑州 450007;2.华北水利水电大学 地球科学与工程学院,河南 郑州 450046)

0 引言

裂隙作为岩溶含水系统的重要组成部分,对岩溶水流运动起到重要作用[1]。裂隙水流运动规律的研究对岩溶水流运动规律、溶质运移规律以及裂隙岩体渗流理论的发展起到重要作用[2-4]。裂隙水流运动一般可以用纳维-斯托克斯方程(简称NS方程)来描述[5]。但是由于NS方程解的复杂性,限制了方程的实际应用。众多研究者按照水流运动实际情况,对NS方程进行了不同程度的简化,第一层将NS方程化为斯托克斯(Stokes)方程;第二层将Stokes方程简化为雷诺方程;第三层将雷诺方程简化为立方定律(CL),由于立方定律的简洁性,得到了广泛的引用。文章以具有四个裂隙面的矩形狭缝裂隙为研究对象(如图1),探讨立方定律在矩形狭缝裂隙中的适用性以及矩形狭缝裂隙水流运动特性。

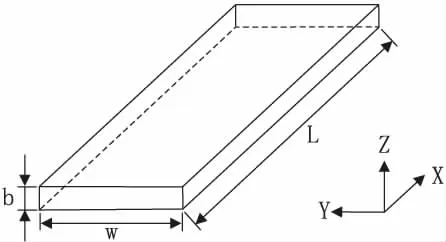
图1 矩形狭缝平行裂隙示意图

NS方程化为Stokes方程的简化条件为:惯性力可以忽略,即流速较小,粘性力占主导地位,雷诺数Re较小。研究者主要从雷诺数出发,研究了Stokes方程的适用条件。Sharp[6],Iwai[7]以及Schrauf[8]利用野外裂隙样本通过室内试验分析得到,当雷诺数大于1到10的某个数值时,惯性力不可忽略。Zimmerman[9]提出当Re(b)/∧b(波长)小于8时,惯性力对渗流量修正系数的影响最高达10%。与NS方程相比,Stokes方程有了很大程度的简化,但是三维Stokes方程的解仍非常复杂。

对LCL进行简化,简化条件为两裂隙面光滑且平行分布(即uy=uz=0),则三维的流体流动可概化为一维流动,设流体沿x轴流动,则沿x轴方向的裂隙渗流量为:

Q=Cb3J

(1)

式中:Q为裂隙间的流量,m3·s-1;b为裂隙开度,m;J为水力坡度,无量纲;C为常数,1 s-1。

方程(1)由于流量Q与裂隙开度b的三次方呈正比,故称为立方定律(Cubic Law,CL)(Boussinesq[16])。对于直线流,常数C可表达为:

(2)

联合方程(1)和(2),可得裂隙渗流量方程为:

(3)

式中:W为裂隙宽度,m;L为裂隙长度,m;ρ为流体密度,kg·m-3;g为重力加速度,m·s-2;μ为动力黏滞系数,N·s·m-2。

将流量方程Q=Wbv以及水力坡度与水头损失之间的关系J=hf/L代入式(3),得到立方定律的另一种表达形式:

(4)

式中:hf为水流通过裂隙时产生的水头损失,m;v为水流流速,m·s-1。

式(4)表明,恒温条件下,水流流经光滑裂隙时的水头损失与水流流速之间呈线性关系。

由于立方定律的简洁性,立方定律得到了广泛应用[17],但由于立方定律的局限性,国内外许多学者主要从裂隙开度[18-19]、裂隙壁面粗糙性[20]、节理粗糙度系数修正[21]、面积接触率[22]等方面进行了研究,并基于各自的研究对象提出了立方定律的修正形式[23]。综合国内外研究成果,绝大多数研究者注重于开放裂隙中立方定律的应用,在实际野外地区,完全开放的裂隙较少存在,矩形狭缝裂隙广泛存在,针对这一问题,以过水断面为矩形的狭缝裂隙(如图1所示)为研究对象,通过数值模拟,对比NS的解,对立方定律的有效性进行研究,提出以极限流速及极限雷诺数来衡量立方定律是否适用,提出适用于矩形狭缝裂隙的修正立方定律,并对裂隙流的水力特性进行了研究,该研究不仅对以往的理论研究进行一定的补充,而且为岩溶含水系统水流运动特征的研究提供理论支撑。

1 矩形狭缝裂隙数值模型的建立

1.1 控制方程

非稳定流条件下,对于不可压缩流体,NS方程[24]为:

(5)

式中:f为体积力,N;p为压力,Pa;t为时间,s。

稳定流情况下,对于不可压缩流体,NS方程为:

ρ(v)v=μ2v-p

(6)

对于两光滑平板间的流体,其运动符合泊肃叶定律,设裂隙两侧壁分布在z=±b/2处,那么流速分布表达式[25]为:

(7)

1.2 边界条件

对不同尺寸的裂隙进行二维和三维模拟,不同模拟情景下,边界条件及裂隙尺寸的设置见表1。

表1 不同模拟情景下边界条件、裂隙尺寸设置

1.3 模型验证(S0模拟结果)

对尺寸为W=2 cm,b=0.840 0 mm,L=20 cm的裂隙中的水流运动进行数值模拟,数值模型设置温度T=13℃,水的密度ρ=999.4 kg/m3,动力粘度μ=0.001 2 Pa·s,重力加速度g=9.8 m/s2,边界条件的设置见表1中模拟情景S0。

水力坡度试验测量值与数值模拟值对比如图2所示。经计算,试验测量值与数值模拟值相对误差((数值模拟值-试验测量值)/试验测量值)在10%以内。

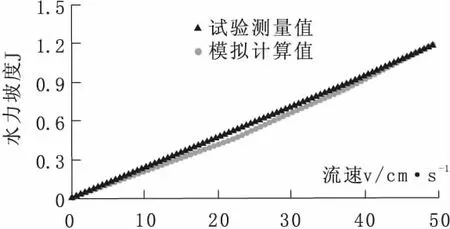
图2 试验测量值与数值模拟值对比图

2 模型结果与分析

2.1 立方定律适用性验证(S1模拟结果)

数值模拟得到7个不同裂隙宽度(W=0.5,1,2,3,4,5,6 cm),6个不同裂隙开度(b=0.05,0.06,0.07,0.08,0.09,0.1 cm),共42个不同尺寸的裂隙水流模拟结果。以数值模拟所得水力坡度与立方定律计算所得水力坡度的比值(J-NS/J-CL)为研究对象(J-NS与J-CL对比图见附件1),来确定立方定律的适用范围。现将不同裂隙宽度(W),不同裂隙开度(b)条件下,J-NS/J-CL随流速变化作对比分析,如图3所示(以W=1,2 cm为例,其余结果见附件2)。结果表明,流速较小时,J-NS与J-CL重合度较高,表明流速较小时,可用立方定律来描述裂隙水流,然而随着流速的增大,J-CL与J-NS之间的差值越来越大,且J-CL均小于J-NS,表明流速较大时,立方定律计算值与实际值偏离越大,立方定律不可以再用来描述裂隙水流运动。

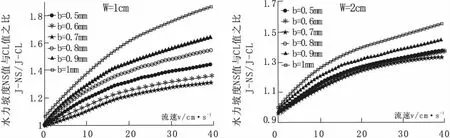
图3 不同裂隙宽度及开度条件下,水力坡度NS值与CL值之比J-NS/J-CL随流速变化

结果表明,在本次研究中(裂隙宽度分布于0.5～6 cm之间,裂隙开度分布于0.05～0.1 cm之间),J-NS/J-CL分布于0.9～2之间,J-CL与J-NS的差值随流速的增大而增大,随裂隙开度的增大而增大,随裂隙宽度的增大而减小,因为流速越大,惯性力的作用越不可忽略。为确定立方定律的适用范围,定义相对偏差为((CL计算值-NS方程模拟值)/NS方程模拟值),相对偏差达到10%时对应的流速称为极限流速(vlim),对应的雷诺数称为极限雷诺数(Relim)。将不同裂隙宽度条件下,极限流速以及极限雷诺数随裂隙开度的变化作对比分析,分别如图4(a)(b)所示。总体来讲,极限流速或极限雷诺数随裂隙宽度的增大而增大,随裂隙开度的增大而减小,说明裂隙宽度越大,开度越小,立方定律越适用。本次研究中,极限流速的最大值为30.08 cm/s,极限雷诺数的最大值为75.2。

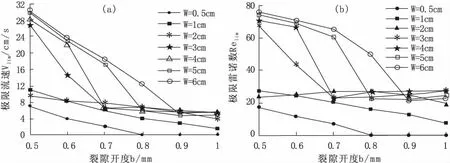
(a)极限流速 (b)极限雷诺数

2.2 修正立方定律的提出

(8)

式中的n值可由S1模拟结果拟合确定(NS方程模拟值与修正立方定律计算值对比结果见附件3)。不同裂隙宽度条件下,n值随裂隙开度的变化如图5所示。结果表明,裂隙开度越大,n值越大;总体来讲,裂隙宽度越大,n值越小,本次研究中,n值分布于1.4～1.9。

图5 不同裂隙宽度条件下,n值随裂隙开度的变化

2.3 矩形狭缝平行裂隙渗透系数分析

根据修正立方定律和达西定律,矩形狭缝平行裂隙渗透系数可以用下式计算:

(9)

分析矩形狭缝裂隙渗透系数随裂隙宽度、裂隙开度以及裂隙宽度与裂隙开度比值的变化(分别如图6(a)(b)(c)所示),同一裂隙开度条件下,渗透系数随裂隙宽度的增大而增大,但增大幅度相对较小。随裂隙开度的增大而增大,增大幅度相对较大。渗透系数随裂隙宽度与裂隙开度比值的增大而增大,通过曲线拟合得到二者之间呈指数关系。本次研究中,矩形狭缝裂隙渗透系数分布于10cm·s-1-70 cm·s-1。

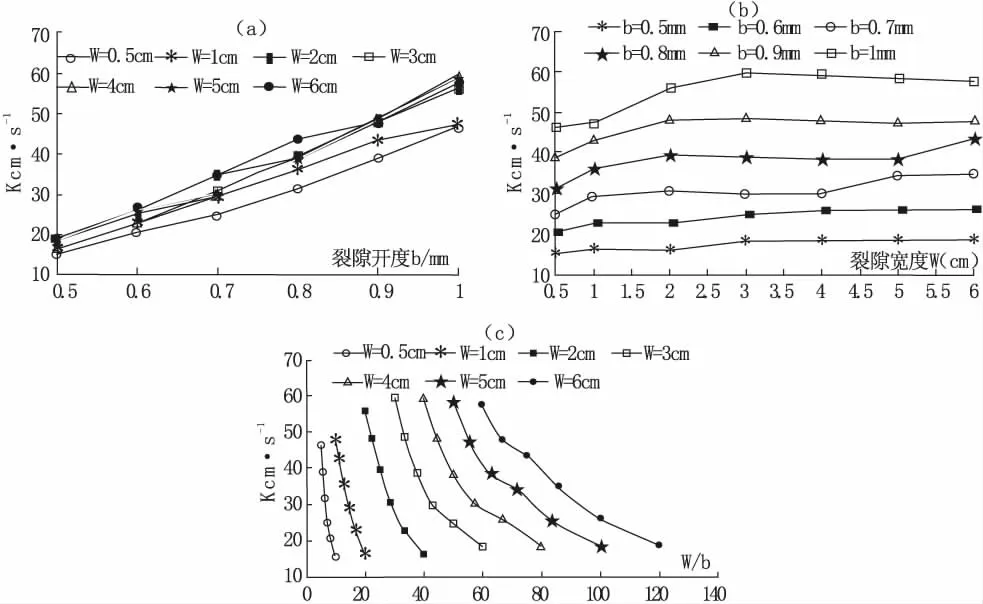
图6 渗透系数随裂隙宽度、裂隙开度以及裂隙宽度与裂隙开度比值的变化图

2.4 流速分布剖面分析

2.4.1 裂隙开度对流速分布剖面影响分析(S2模拟结果)

不同裂隙开度条件下,X=10 cm处流速分布如图7所示(以b=0.05,0.1 cm为例,其余结果见附件4)。从图中可以看出,二维裂隙面流速剖面形状变化与理想泊肃叶流体流速变化形状基本一致,数值上有所差异。流速的最大值位于裂隙中心线处。流速最小值位于裂隙壁处且为零。分析不同开度条件下,流速模拟值与泊肃叶值之差(绝对偏差)及相对偏差沿质点位置(Z轴)的变化(如图8所示),绝对偏差随裂隙开度的增大而增大,且离裂隙中心线(X轴)越近,偏差越大。相对偏差沿质点位置(Z轴)呈波动变化,变幅很小;相对偏差随裂隙开度的增大而增大,表明裂隙开度越大,流速分布越不符合标准抛物线分布。

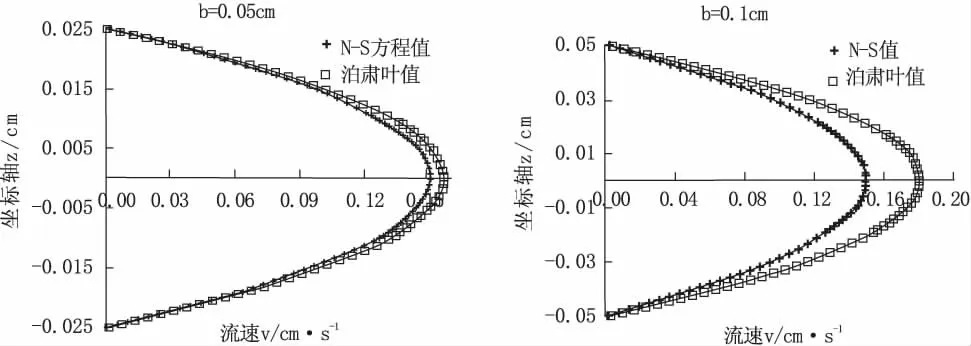
图7 不同裂隙开度条件下,流速剖面分布

图8 不同开度条件下,流速模拟值与泊肃叶值的绝对偏差及相对偏差沿质点位置(Z轴)的变化图

2.4.2 流速大小对流速分布影响分析(S3模拟结果)

不同流速条件下,流速分布剖面如图9所示。从图中可以看出,无论流速大小,模拟所得流速分布大致符合抛物线分布,流速最大值位于裂隙中心线处(即X轴上),离裂隙壁越近,流速越小,在裂隙壁处流速为零。分析不同流速条件下,流速模拟值与泊肃叶值之差(绝对偏差)及相对偏差变化(如图10所示),流速越大,绝对偏差越大,在裂隙中心线处最大,离裂隙壁越近,偏差越小。而相对偏差随流速的变化幅度相对较小,表现为集中型。

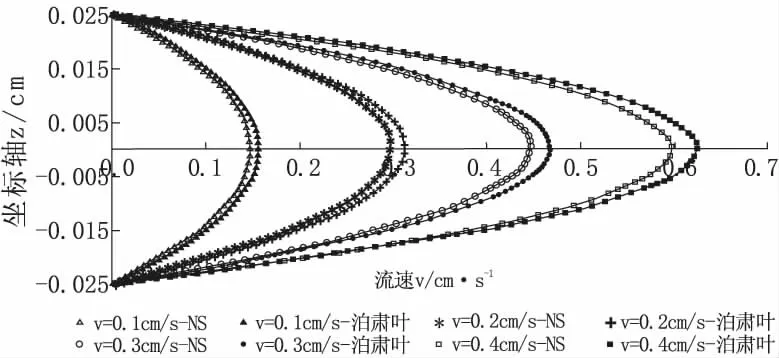
图9 不同流速条件下,流速剖面分布对比(NS值与泊肃叶值对比图)

图10 不同流速条件下,流速模拟值与泊肃叶值的绝对偏差及相对偏差沿质点位置(Z轴)的变化图

2.4.3 裂隙宽度对流速分布影响分析(S4模拟结果)

取XY面中心线处Z=b/2,沿X=L/2质点流速为研究对象,不同裂隙宽度条件下,流速分布如图11所示,从图中可以看出流速值沿Y轴波动较小,在裂隙壁处骤减为0,随着裂隙宽度的增大,流速波动幅度变小,裂隙宽度大于等于3 cm(对应的裂隙宽度与开度之比W/b≥40)的四条曲线重合度较高,表明随着裂隙宽度及裂隙宽度与开度之比的增大,裂隙宽度的大小对流速分布曲线的影响减弱。

图11 不同裂隙宽度条件下,XY面中心线处Z=b/2,沿X=L/2质点流速分布图

3 结语

以矩形狭缝平行单裂隙为研究对象,对不同尺寸的矩形狭缝平行裂隙进行NS方程模拟计算,并将模拟结果与CL计算结果进行对比,首先对立方定律在矩形狭缝平行裂隙中的适用性进行验证,发现流速较小时,CL值与NS值吻合较好,流速越大,立方定律越不适用,进而提出极限流速和极限雷诺数的概念来确定立方定律在矩形狭缝裂隙中的适用范围,在本次研究中,极限流速的最大值为30.08 cm/s,极限雷诺数的最大值为75.2;基于修正立方定律和达西定律,提出矩形狭缝裂隙中立方定律的修正形式,式中的参数n值分布与1.4～1.9之间,矩形狭缝裂隙渗透系数随裂隙宽度的变化幅度较小,随裂隙开度的增大而增大,随裂隙宽度与裂隙开度比值的增大而增大。分析流速剖面分布随裂隙开度、裂隙宽度以及流速的变化规律,结果表明裂隙开度越大,流速越大,流速分布越不符合标准抛物线分布;裂隙宽度越大,对流速分布曲线的影响越弱。