BDS-3 PPP-B2b精密轨道辅助非差非组合PPP-RTK
查九平,张宝成,刘 腾,张 啸,侯鹏宇,袁运斌,李子申
1. 中国科学院精密测量科学与技术创新研究院大地测量与地球动力学国家重点实验室,湖北 武汉 430071; 2. 广州市城市规划勘测设计研究院,广东 广州 510060; 3. 中国科学院空天信息创新研究院,北京 100094
BDS-3于2020年7月31日正式开始提供全星座全球服务,并提供了包含精密单点定位技术(PPP)在内的7种特色服务[1-2]。其中,BDS-3星基PPP服务(PPP-B2b)通过其高轨道卫星的B2b信号搭载PPP精密卫星产品,并以500 bps带宽向地面进行广播,辅助实现亚太地区分米级精度的实时绝对定位[3]。PPP-B2b精密卫星产品主要包含精密卫星轨道与钟差相对于广播星历的改正数、精密卫星码偏差及用户测距精度指数,支持BDS-3、GPS、GLONASS及Galileo四系统所有可用卫星[4]。
BDS-3 PPP-B2b服务是继日本QZSS CLAS之后的第2个由官方机构提供的星基PPP服务[4-5]。该服务相较于传统国际GNSS分析中心(IGS)提供的PPP服务,其主要优势是通过卫星进行广播,可规避互联网对用户定位的影响,在互联网未覆盖或自然灾害等造成互联网异常等地区仍能提供精密定位服务[6]。相较于现有其他官方或商业星基PPP服务,PPP-B2b主要优势是其精密产品解算仅基于中国境内监测站数据与星间链路数据进行,降低了对海外测站的依赖,可进一步降低系统成本并增加系统连续性与稳定性[3,5]。PPP-B2b服务上线后,国内外许多学者进一步对其进行了深入研究,不仅根据实践应用对PPP-B2b接口文件(ICD)进行了补充,如精密轨道为相位中心产品、BDS-3基准频率为B3I及PPP-B2b服务范围等;还系统全面地评估了PPP-B2b精密产品精度与用户定位性能,如空间信号测距误差(SISRE)的均方根误差(RMS)为分米级与标准差(STD)为厘米级、定位精度为静态厘米级与动态分米级、收敛时间优于30 min等,可为PPP-B2b应用提供更细致的指导[7-12]。此外,部分研究者基于PPP-B2b服务开展了其他相关研究,如基于PPP-B2b服务进行实时同震位移反演,其卫星播发可有效规避地面互联网影响,同时其绝对坐标可有效规避灾害时期传统RTK/NRTK中参考站形变影响[13];基于PPP-B2b服务进行时间传递,与传统PPP时间传递方法相比,具有成本低、不依赖于地面通信网络等优势[14]。如上所述,PPP-B2b服务特色显著、优势突出,但仍无法回避PPP技术收敛慢与精度低等问题,限制其在工程实践中的广泛应用。
文献[15]提出精密单点实时动态定位技术(PPP-RTK)的概念,即通过联合PPP服务中精密卫星产品与区域稀疏参考站网观测数据解算卫星相位偏差与区域大气延迟等产品,并单向播发给用户进行改正,最终实现快速或瞬时模糊度固定的精密绝对定位。PPP-RTK技术主要分为非差组合法和非差非组合法,区别在于前者分步估计各类参数且其相位偏差通过组合观测值间接分离获得[16-17],而后者则直接同步估计精密卫星偏差与大气延迟等产品[18-19]。相比较而言,非差非组合PPP-RTK方法理论更为严密、各类参数间自洽性好且易于多频多模扩展,具有更好的应用前景[20]。近年来,国内外学者对PPP-RTK技术进行了大量理论研究,涉及多频多模扩展[21]、不同方法分析比较[20]、模糊度整数固定[22]、参数优化估计[23]、多尺度应用性能评估[24]、多源融合应用[25]及区域大气建模[26]等,但现有研究多基于事后进行,区域大气延迟实时建模与应用仍是制约PPP-RTK技术发展的关键问题。其中,电离层延迟参数多、与其他参数高度耦合且其物理环境复杂不易模拟,因而电离层延迟的数据压缩与准确表达是区域大气延迟建模与应用的重中之重[27]。当前主流的电离层延迟实时建模方案为广域球(冠)谐约束、区域多项式模拟与局域残差格网补充三者联合,显然该方案实施成本非常大,尤其是电离层延迟残差格网数据量巨大[5,28]。此外,受限于电离层各向异性及其投影函数精度不高,高精度电离层延迟建模应直接基于其斜延迟进行[27,29]。然而,电离层斜延迟参数与接收机码偏差参数难以分离,现有方法采取差分或共视方法规避该问题并对电离层斜延迟进行建模,但一定程度地增加了建模复杂度并降低PPP-RTK应用性能[17,29-30]。
为解决BDS-3稀疏参考网定位增强参数估计与区域电离层延迟建模及应用问题,本文采用电离层加权非差非组合PPP-RTK方法(IWUDUCPPP-RTK)同步估计精密卫星偏差与大气延迟等参数,并基于PPP-B2b精密卫星轨道产品及京津区域稀疏参考网进行了初步试验[31]。其中,IW UDUC PPP-RTK方法较传统UDUC PPP-RTK方法不仅增强了服务端参数估计,还主要实现区域电离层延迟参数与参考站接收机码偏差参数的解耦。基于此,本文构建了简单有效的区域大气延迟函数模型,有效压缩了区域大气延迟播发数据量。
1 方 法
1.1 电离层加权非差非组合PPP-RTK模型
GNSS原始观测值的线性化方程可表示为
(1)
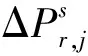
式(1)中部分参数线性相关,不能直接获得所有参数的无偏估值,需根据S-basis消秩亏理论对参数进行重整,获得感兴趣参数新的可估形式[23]。同时,为解耦电离层延迟参数与接收机码偏差参数,本文采用IW UDUC PPP-RTK模型进行参数估计[31]。该模型考虑同一颗卫星到相距几百千米的两个测站所经历的电离层斜延迟量近似相等[32],进而构建了站间单差电离层伪观测值来增强传统UDUCPPP-RTK模型。IW UDUC PPP-RTK网模型为
(2)
式中,参考站坐标由真值坐标先验改正,不进行估计;QI表示电离层伪观测值的权逆阵,其表达如下
(3)
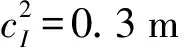
(4)
本文中p和q分别表示基准站和基准星,基准站一般选取测区中心测站,基准星一般选取测站高度角最高的卫星。此外
(5)
如式(4)所示,①模糊度可估形式为双差整数,可直接进行模糊度固定;②重组后的模糊度参数与接收机、卫星相位偏差参数完成解耦,式(2)可直接估计具有整数特性的模糊度和各频点卫星相位偏差,该卫星相位偏差估值可直接发送给用户端进行改正;③所有电离层延迟参数都包含相同的接收机码偏差,有利于电离层延迟产品后续建模。
(6)
(7)
(8)
1.2 区域大气模型
本文假设电离层延迟集中在某个薄层,而投影在该薄层的各个参考站相对位置与地面等价,因而可直接基于参考站地面经纬度(φr,θr)相对于测区中心经纬度(φ0,θ0)的差值(Δφr=φr-φ0,Δθr=θr-θ0),对单星电离层斜延迟进行二维二阶泰勒展开。该模型表示如下

(9)
式中,βi(i=0,1,…,5)表示电离层斜延迟多项式系数,其中β0为与参考站无关项,βi(i=1,2,…,5)为与参考站经纬度相关项。
(10)
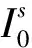
然而,传统PPP-RTK模型中[17,33],电离层可估形式为
(11)
式中,br,GF表示参考网接收机几何无关码偏差。显然,不同接收机,br,GF不同,其不同部分在建模过程中会被吸收进与参考站经纬度相关项中,与实际物理意义不符,而且难以被接收机相关参数吸收,进而造成用户端未模型化误差,影响用户位置等参数估计。
此外,为保证PPP-RTK用户定位的精度与可靠性,本文将电离层延迟估值的方差信息传递给用户端以构建式(6)中电离层伪观测值的随机模型。然而,电离层延迟估值的方差数据较多,直接传输数据量较大,因此需要建模约化为模型系数。由于同一卫星对区域内不同测站几何结构较为接近,因此本文整网估计的电离层延迟估值的方差较为接近,可简化建模。同时,考虑测区边缘与测区外服务精度较差,故采用高斯函数辅助方差信息建模,以实现对相应区域精密应用进行降权。该模型为
(12)
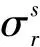
本文对流层延迟模型使用H1QM4模型[34]。该模型考虑了对流层延迟随平面位置和高程的线性变化,同时考虑了对流层延迟在北方向和东方向具有不同的梯度。该模型表示如下
τr=α0+α1Δφr+α2Δθr+α3Δφr·Δθr+α4hr
(13)
式中,α0,α1,…,α4表示对流层延迟多项式系数;hr为参考站r的大地高。
由于本文网端进行整网参数估计且各参数之间相互解耦,在提高各类产品估计精度的同时,也间接提高了大气建模精度,因此不需要传统大气残差格网辅助, 仅利用简单多项式模型就可获得较好的应用精度,继而可节省实时大气延迟产品的传输数据量。此外,式(9)、式(12)及式(13)中模型系数采用单历元等权最小二乘估计获得。
2 试验配置及结果分析
2.1 试验配置
如图1所示,试验数据由我国京津区域8个参考站和2个用户站的BDS-3/GPS双系统双频观测值构成。参考站相邻站间距为79.4~253.6 km。参考站及用户站接收机类型均为UR4B0-D,除BFGY用户站天线类型为TRM55971.00 NONE外,其余测站天线类型均为HXCCGX601A HXCS。试验日期为2021年2月19日。本文采用的真值坐标由加拿大NRC的CSRS-PPP在线软件提供,采用其单天静态GPS+GLONASS模糊度固定解,本文网模型中参考站坐标由此真值坐标先验改正,用户模型估计的测站坐标则以此为参考真值来评估精度。后文大气延迟建模精度评估中,参考大气延迟为PPP-AR估计的大气延迟值,简称PPP-AR估计值。本文主要解算策略见表1。此外,本文PPP-RTK服务端每5 s估计一组大气延迟值,并直接进行空间建模,再发送给用户进行使用;用户端每次使用所接收的最新产品,而产品与观测数据最大时延控制在30 s内。本文PPP-RTK解算仅使用BDS-3 PPP-B2b精密卫星轨道产品,而后文用于对比分析的PPP则基于BDS-3 PPP-B2b精密卫星轨道、钟差及码偏差进行解算。

表1 主要解算策略

图1 测站分布Fig.1 Stations distribution
2.2 结果分析
图2、图3分别为TJYC站BDS-3、GPS电离层斜延迟PPP-AR估计值(简称估计值)与PPP-RTK服务端多项式模型值(简称模型值)对比结果。其中,电离层斜延迟估计值(上)与模型值(中)时间序列较为接近,但存在整体偏移,主要原因为前者包含TJYC站几何无关接收机码偏差,而后者包含网端基准站几何无关接收机码偏差。因此,计算电离层斜延迟估计值与模型值之差(下)时需减去单历元所有卫星平均值,以消除二者基准偏差。统计结果显示,本文电离层延迟模型值的RMS约为2.2 cm(BDS-3)/2.4 cm(GPS),充分满足文献[35]提出的有效电离层延迟产品精度0.7 TECU(约为11.4 cm)。
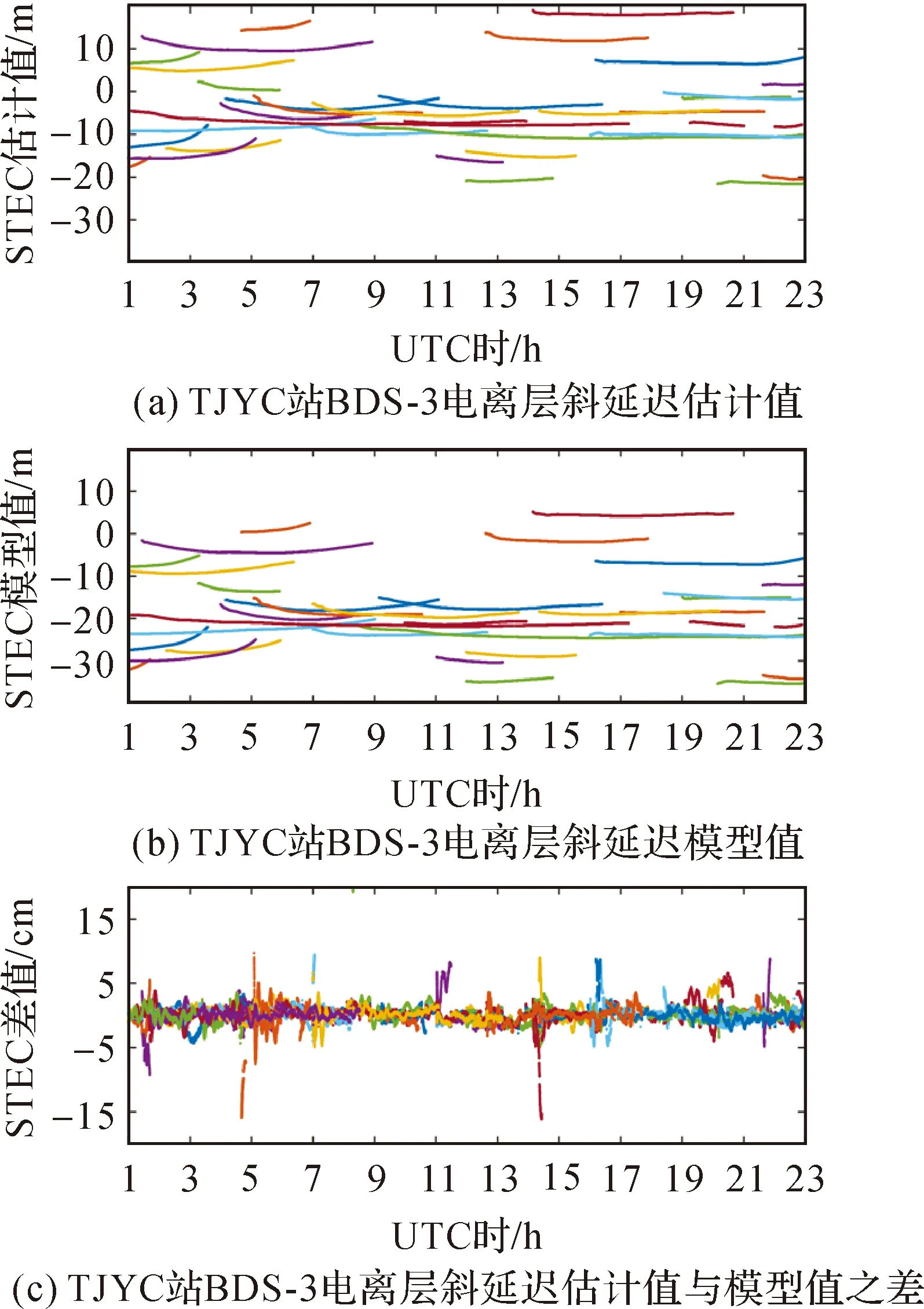
图2 TJYC站BDS-3电离层斜延迟精度Fig.2 Accuracy of the ionospheric slant delays for BDS-3 on TJYC station

图3 TJYC站GPS电离层斜延迟精度Fig.3 Accuracy of the ionospheric slant delays for GPS on TJYC station
图4为TJYC站天顶对流层湿延迟PPP-AR估值(简称估计值)和PPP-RTK服务端多项式模型值(简称模型值)对比结果。其中,天顶对流层湿延迟已扣除UNB3m模型计算的天顶对流层湿
延迟。如图4所示,天顶对流层湿延迟估计值(图3(a))与模型值(图3(b))时间序列较为接近,但后者较前者平滑,主要原因为服务端采用整网参数估计, 而PPP-AR端为单站参数估计; 二者之差被进一步统计在图3(c)中,其RMS值约为0.29 cm。
图5为TJYC站基于PPP-B2b精密卫星产品的多系统静态仿动态PPP和PPP-RTK定位时间序列。PPP结果显示,单BDS-3与BDS-3+GPS定位精度相当, 其定位误差半小时内可收敛,且水平方向稳定在±0.1 m内,垂直方向稳定在±0.2 m内;单GPS定位精度较差,收敛后其定位误差,水平方向稳定在±0.2 m内,垂直方向稳定在±0.5 m内。PPP收敛后,单BDS-3与BDS-3+GPS位置解RMS在厘米级,而单GPS位置解RMS水平接近0.1 m且垂直接近0.2 m。PPP-RTK结果显示,单BDS-3与BDS-3+GPS定位精度相当,其定位误差可“瞬时”收敛,且水平稳定在±2 cm内,垂直稳定在±5 cm内;单GPS定位结果总体表现为噪声较大,但未存在如PPP时间序列的较大趋势变化。表2为PPP-RTK定位精度统计结果,BDS-3/BDS-3+GPS策略均达到水平毫米级与垂直厘米级的定位精度。本文所示GPS单系统定位性能较BDS-3单系统差有两方面原因:①PPP-B2b精密轨道解算未使用全球网,但BDS-3有星间链路增强,而GPS无星间链路增强;②接收机追踪到的可用GPS卫星较少,而且粗差探测、产品匹配与截止高度角控制等进一步减少了GPS卫星数。此外,表2中统计的PPP定位精度为收敛半小时后结果,而PPP-RTK用户定位几乎瞬时收敛,所以统计全序列定位精度。
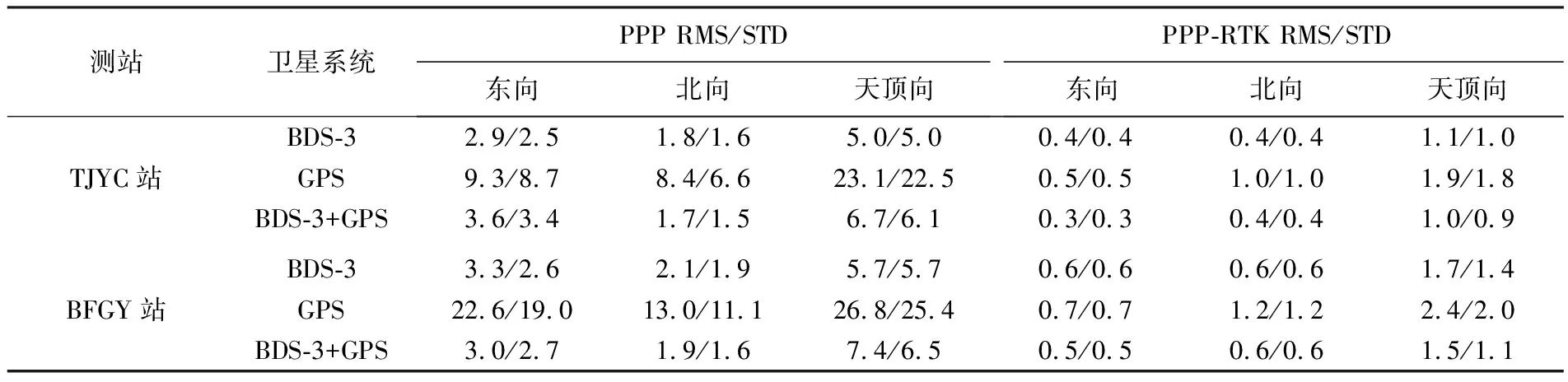
表2 基于BDS-3 PPP-B2b的PPP及PPP-RTK位置解RMS与STD统计
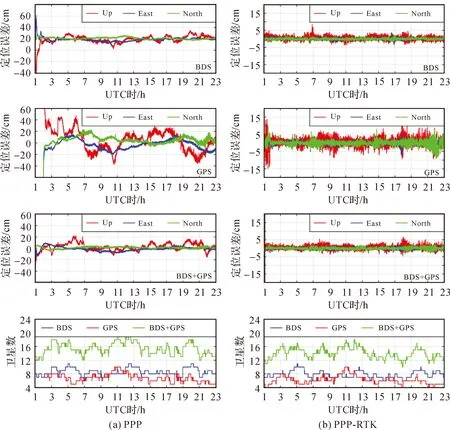
图5 TJYC站基于BDS-3 PPP-B2b精密卫星产品的静态仿动态PPP及PPP-RTK定位时间序列Fig.5 Time series of kinematic positioning errors on station TJYC estimated by PPP and PPP-RTK based on precise satellite products of BDS-3 PPP-B2b, respectively
图6为BFGY站基于PPP-B2b精密卫星产品的多系统静态仿动态PPP与PPP-RTK定位时间序列。BFGY站定位结果与TJYC站相近,但其PPP-RTK定位结果中高程方向有略微系统偏移,总体精度保持在相同量级。此差异可能因为TJYC站与网端参考站保持相同的接收机类型和天线类型,而BFGY站天线类型与网端参考站天线类型不一致。
PPP-RTK技术不仅提高PPP定位精度,还主要提高定位收敛速度。理论上模糊度固定成功后,可立刻实现高精度定位,但本文采用部分模糊度固定策略,参与固定的模糊度随着滤波收敛逐渐增加,因此固定解时间序列也存在一个收敛过程。为统计PPP-RTK定位收敛时间,用户端每10 min冷启动一次。图7为PPP-RTK定位收敛时间序列,表3为相应统计结果。如图7所示,所有弧段基本首历元即实现模糊度固定,并且单BDS-3和BDS-3+GPS平均瞬时收敛至水平2 cm与垂直5 cm。如表3所示,单BDS-3超95%弧段绝对误差可在6 s内收敛到水平2 cm与垂直5 cm,收敛到同等精度BDS-3+GPS只需2 s,而单GPS需要10 s左右。图7中,红色虚线为定位误差阈值(水平2 cm/垂直5 cm),灰色实线为样本弧段,蓝色实线为平均值。
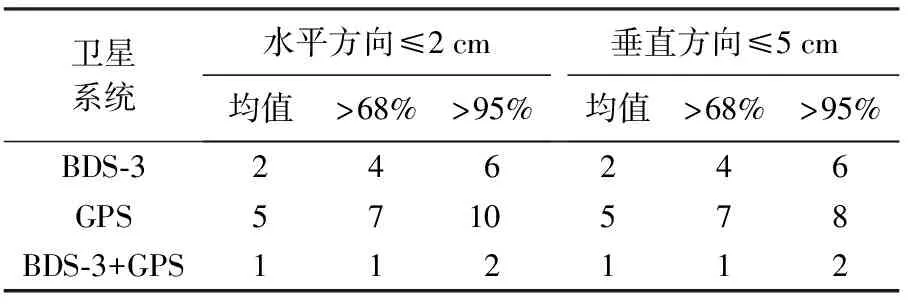
表3 基于BDS-3 PPP-B2b精密卫星轨道产品的PPP-RTK收敛时间

注:红色虚线为定位误差阈值(水平2 cm/垂直5 cm);灰色实线为样本弧段;蓝色实线为平均值。图7 基于BDS-3 PPP-B2b精密卫星轨道产品的PPP-RTK收敛行为Fig.7 Convergence behavior of the PPP-RTK based on precise satellite orbit products of BDS-3 PPP-B2b
3 总 结
本文首先采用IW UDUC PPP-RTK模型同步估计精密卫星偏差与大气延迟产品,该模型利用站间单差电离层伪观测值对传统UDUC PPP-RTK进行约束,在增强网端参数估计的同时,规避了参考站接收机码偏差影响电离层延迟建模的问题。其次,结合本文电离层延迟参数结构及精度优势,构建了单星电离层斜延迟多项式模型,相比于传统多项式联合残差格网的电离层延迟模型,本文仅采用多项式建模可显著减少电离层斜延迟数据播发量;同时,将电离层延迟估值的方差信息进行建模,并作为电离层延迟产品的随机信息来约束用户定位,以提高用户定位的精度及可靠性。在上述模型基础上,联合BDS-3 PPP-B2b精密卫星轨道产品与京津区域稀疏参考站网观测数据,进行了初步的星地融合定位试验。以下为相关的结论:
(1) 以静态PPP-AR估计的大气延迟作为参考,本文所构建的单星电离层斜延迟建模精度约为2.2 cm(BDS-3)/2.4 cm(GPS),而天顶对流层延迟建模精度为0.29 cm。
(2) 本文利用PPP-B2b精密产品进行动态PPP试验,单BDS-3可在半小时内实现收敛,且收敛后精度水平约为3 cm,垂直约为5 cm。
(3) 本文基于PPP-B2b精密轨道产品进行PPP-RTK初步试验,其中单BDS-3超95%弧段绝对误差可在6 s内收敛到水平2 cm与垂直5 cm,而BDS-3+GPS仅需2 s。单BDS-3与BDS-3+GPS可实现水平毫米级与垂直厘米级的快速模糊度固定的精密绝对定位。

