旋挖钻机截齿的破岩机理及优化研究

刘先珊 牛万保 许明

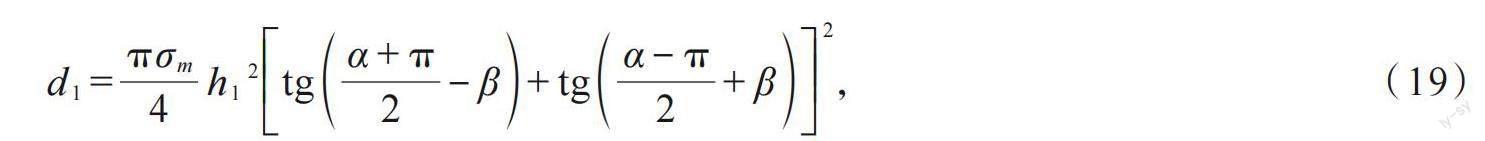
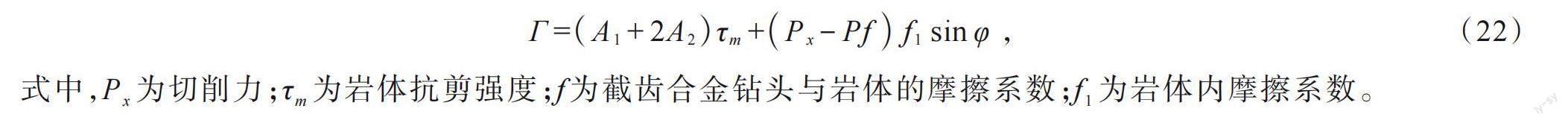
doi：10.11835/j.issn.1000.582X.2023.09.007

收稿日期：2022-10-07

基金項目：国家自然科学基金资助项目（52279094）；重庆市自然科学基金资助项目（CSTB2023NSCQ-MSX0069）。

Supported by the National Natural Science Foundation of China（52279094）， Chongqing National Science Foundation（CSTB2023NSCQ-MSX0069）.

作者简介：刘先珊（1978-），女，博士，教授，主要从事岩土工程渗流、多场耦合理论及数值方法研究，（E-mail）liuxianshan@163.com。

摘要：旋挖钻机成孔的显著优势备受关注，但实际钻孔很难达到理想的破岩效果，揭示复杂地层赋存环境的钻头破岩机理是关键。文中基于Boussinesq问题的求解，得到动力头压力和扭矩作用于截齿时的岩石受力及位移，推导截齿破岩时的侵入力及切削力表达式。建立单截齿破岩的三维数值模型，获得钻头钻进中截齿的侵入力及切削力变化规律，对比理论结果以验证数值模型的可行性。基于旋挖钻机双截齿破岩过程的数值模拟，分析钻进中的岩体力学响应及裂纹演化以揭示截齿的破岩机理，探讨不同截齿布置的旋挖钻机破岩力特征，阐明截齿倾角或偏斜角增大都将不同程度地改变破岩力大小。进一步分析截齿布置方式与不同类型地层组合的破岩效率，结果表明，截齿倾角或截齿偏斜角或截齿间距相等时，由软到硬地层的破碎比功逐渐增大，且钻进某一地层的破碎比功先减小后增大，存在最优的截齿布置使得钻进效率最高。研究成果可为旋挖钻机截齿设计的优化和破岩效率的提高提供理论依据。

关键词：旋挖钻机；数值模拟；截齿破岩；截齿布置；破岩效率；优化

中图分类号：TU45          文献标志码：A      文章编号：1000-582X（2023）09-052-14

Fragmentation mechanism and optimization of the picks in rotary drilling gig

LIU Xianshan^a，b， NIU Wanbao^a，b， XU Ming^a，b

（a. Key Laboratory of New Technology for Construction of Cities in Mountain Area， Ministry of Education; b. School of Civil Engineering， Chongqing University， Chongqing， 400045， P. R. China）

Abstract： The significant advantages of the rotary drilling rig for boring have attracted increasing attention. However， achieving ideal fragmentation efficiency in practical drilling remains challenging. Therefore， it is crucial to understand the fragmentation mechanism in the stratum environment. By solving the Boussinesq problem， the force and displacement exerted on the picks by the power head， as well as the penetrating force and cutting force under picks fragmentation conditions， have been determined. Additionally， a 3-Dimension numerical model for a single pick has been proposed to analyze the variation in penetrating force and cutting force. The results have been calibrated with theory to validate their reliability. Furthermore， a numerical simulation involving two picks has been conducted to describe the mechanical response and cracking evolution， thus revealing the mechanism of the pick fragmentation. In addition， the fragmentation forces exerted by picks with different arrangements have been extensively discussed， highlighting that the pick inclination or deviation angle has a significant impact on fragmentation force. Finally， the fragmentation efficiency with considering the picks arrangement in different strata has been thoroughly investigated. The findings demonstrate that specific work increases as the machine drills from soft to hard formations， while maintaining the same pick inclination， deviation angle or spacing. Furthermore， the corresponding value firstly decreases， then increases for a given stratum， indicating that the optimized arrangement of picks yields the highest efficiency. These achievements provides theoretical support for the optimization of picks and improvement of fragmentation efficiency.

Keywords： rotary drilling rig; numerical simulation; pick fragmentation; picks arrangement; fragmentation efficiency; optimization

近年来，国家高速公路、铁路、桥梁及城市基础建设快速发展，越来越多地涉及深基础工程，而桩基础作为其重要形式，合理可靠的成孔方式是关键。旋挖钻机^[1]（见图1（a））相对于传统成孔方式，适用于土层、风化岩层、复合地层等，可实现低成本、高质量及快速施工，优势凸显。现有旋挖钻机的施工过程表明，单一的静压碎岩不仅降低旋挖和进尺速度，且磨损钻具严重，充分协同其动力头压力及扭矩作用，才能有效增大破碎深度、破碎体积和破岩比能。因此，结合地层赋存环境，分析旋挖钻机钻头侵入和旋转切削地层的破岩特性，是实现高效破岩成孔的关键。

一些学者结合理论分析、试验及数值模拟对机械破岩进行研究。在理论研究方面，Marshall^[2]基于弹性接触理论，获得压头侵入岩石的应力-应变规律，分析切削岩石的Hertz裂纹发展；Evans^[3]建立了镐型截齿平面截割截槽对称的破煤模型，基于岩体拉伸破坏理论推导截割力的理论计算公式；刘春生等^[4]建立了镐型截齿截槽非对称的截割力学模型，提出截齿轴向倾 斜布置角度的取值范围；Gao等^[5]提出了镐型截齿峰值切割力的理论模型，并进行了预测；刘晋霞等^[6]建立了镐型截齿旋转截割力模型，分析截割力与截割角及半锥角的关系；蔡灿等^[7]考虑钻压和围压，基于空腔膨胀理论建立力学与数学模型，解释单齿冲击下的岩石破碎机制。上述理论模型与岩石力学性质和刀具作用参数有关，忽视了刀具与岩石的接触特性。在试验研究方面，赵伏军等^[8]通过动静载实验分析侵入载荷与裂纹的关系，阐明冲击静压切削组合的破岩效果；Geng^[9]通过切割实验分析了旋挖速度对其切削深度的影响；刘春生等^[10]基于单齿截割实验得到的阻力谱，建立了滚筒截割阻力实验-理论的综合模型，提出截割阻力理论模型的3种算法；Li^[11]建立钻头的几何模型，通过实验分析钻头表面形貌对其切削过程的影响。在数值模拟方面，戴珊珊^[12]基于ABAQUS建立截齿截割煤岩的数值模型，分析截齿应力分布、截割载荷及煤岩的断裂路径；江红祥等^[13]结合断裂力学及有限元方法，模拟单齿切割不同深度的4种岩石截割过程，模拟结果与理论计算、试验结果相吻合；Saksala等^[14]在LS-DYNA中引入MHJC动态本构模型，研究不同围压或不同岩层形貌的破碎岩体体积；Marion等^[15]运用LS-DYNA模拟旋挖钻进破碎岩石的能量耗散过程，建立旋转钻头破碎岩石能量的分形模型；周子龙等^[16]基于颗粒流软件，分析不同围压与不同镐形截齿侵入角的破岩过程，得出围压0～20 MPa、截齿侵入角45°～60°最利于破巖。以上室内试验与数值模拟阐明了机械破岩过程研究的技术方法，为充分认识旋挖钻机的破岩机理提供了支撑。

截齿（见图1（b））作为旋挖钻机的重要组成部分，钻进中与岩层接触受力特性的研究是揭示旋挖机破岩机理的理论基础。文中依托重庆市某高压输变电站的深基坑桩基工程，根据现场SR280R旋挖钻机截齿破岩的动力头压力及扭矩，进行截齿破岩理论分析，基于ABAQUS软件的截齿钻进动力三维数值模型，分析钻进过程中的截齿破岩力特性，对比理论结果以验证三维数值模型的可靠性；进一步探讨不同截齿布置对截齿破岩力及破碎比功的影响规律，分析不同类型地层的截齿破岩力及破碎比功特性。研究成果可为优化旋挖钻机的截齿布置方案及提高实际地层的旋挖效率提供科学依据。

1旋挖钻机截齿破岩受力分析

1.1旋挖钻进岩体的重要作用力

分析现场旋挖钻机破岩过程的钻进参数，发现入岩参数主要为轴向压力和水平切削力，通过旋挖钻机的动力头总压力和扭矩来体现。根据机械原理，可得到动力头总压力和扭矩的表达式。

动力头的总压力为

动力头扭矩为

1.2截齿法向作用岩石的接触力效应

图2所示为截齿法向作用于岩石，当不计岩体自重时，可基于Boussinesq.T.V 求解岩体内部任一点的应力。

得到法向荷载作用于岩体任一点的应变分量：

当z=0时，即截齿法向作用于岩体表面，其应变为

假设均布荷载为

根据Boussinesq.T.V问题给出的位移解公式（10），采用叠加原理计算岩体表面的法向位移：

由此可见，法向荷载与侵深成比例，即截齿旋挖钻进中的接触力与侵深成比例关系。

1.3单截齿破岩时的受力分析

1.3.1 单截齿破岩时的轴向力

旋挖钻进动力头压入过程中，轴向力使得岩体形成破碎坑，其单截齿破坏岩体的计算模型如图4所示。对单截齿而言，至少要满足单位面积上的压力超过岩石的单轴抗压强度，满足以下公式：

则轴向力至少满足如下表达式：

1.3.2 单截齿破岩时的切削力

截齿斜向侵入岩体时产生相对滑动，破坏面上将产生摩擦阻力。截齿切削形成剪切过程中需要克服的力，如图 4（b）所示，即面ABB' 、侧面ABC' 和侧面AB'C 产生的岩体抗剪切阻力和破坏面上的摩擦力。

由公式（24）可知，旋挖钻进过程中的轴向力越大，切削力越大，对应的旋挖钻机扭矩也越大。

2旋挖钻机截齿破岩的数值建模及验证

旋挖钻进过程是先通过侵入力作用于截齿，使岩石产生一个较小的破碎坑，形成发散式裂纹扩展，再通过钻筒的旋转带动截齿产生切向力，完成岩石的旋挖切削破碎，其过程体现了刀具对岩石的冲击、岩石破碎等动-静荷载的组合效应，其力学响应具有高度的非线性特征。为了更有效地描述旋挖钻机的成孔过程，深入认识截齿的破岩特性是关键。基于ABAQUS软件研究截齿与岩体的相互作用，对比理论结果，阐明该数值模型再现截齿破岩过程的适用性和可靠性。

2.1三维数值模型建模及验证

根据SR280R旋挖钻机的截齿特征，采用ABAQUS建立三维数值模型，如图5所示。数值计算中，不考虑截齿磨损，将其简化为刚体，选用弹性本构模型，力学参数如表1所示。岩体单元类型为8节点六面体单元C3D8R，选用扩展Drucker-Prager本构模型，设置失效准则为剪切损伤，屈服应力阈值150 MPa，断裂应变阈值0.15，剪应力比0.33，应力比0.0001，损伤演化的破坏位移阈值2 mm，其力学参数如表2所示。

2.2模型验证

截齿破岩中的侵入力主要是法向力，其大小决定截齿侵入岩石的深度；切向力是钻头旋转扭矩形成的切屑力，截齿瞬时切削代表旋挖钻机产生的扭矩作用。因此，研究截齿侵入力与侵深以及切向力与切割位移的关系，对理解旋挖钻进的岩石破碎机理具有重要意义。基于ABAQUS三维数值模型模拟单截齿破岩过程，获得侵入力及切向力与位移的关系，如图6所示。由图可知，截齿法向力开始随侵深增大而增大，侵深2 、3.25 、4.25 、4.75 mm时，其法应力突降形成谷点，且谷点出现的侵深间隔越来越小，说明侵入岩石的过程中，初始裂纹代表岩石突然破碎，截齿呈现跳跃性侵入，也阐明了法向力增加可加快裂纹扩展，岩块破碎速率增加，截齿跳跃性的侵入频率增大。图6给出了竖向侵入力与侵深的变化关系，其变化趋势与理论结果基本吻合，验证了三维数值模型模拟旋挖钻进过程的可靠性。另外，切向力随位移呈循环式波动，当切向力达到一定临界值时，截齿突然跃进，表明岩石在切削作用下产生拉破坏，出现体积较大的岩块剥离现象；当岩块断裂剥离，切向力快速下降，切向位移1.8～2.7 mm时出现了切向力快速下降；随后，截齿继续向前接触新岩面，切向力突增，切向位移3～3.3 mm时出现了较大的切向力，如此跃进-接触-跃进循环，呈现切向力-切向位移变化趋势，与理论分析的变化规律吻合，进一步验证了三维数值模型的可靠性。

3旋挖钻机截齿的破岩机理

基于第三节的数值模型，建立双截齿三维数值模型，分析旋挖钻进中的岩体力学响应特征及裂纹演化规律，揭示旋挖钻机截齿的破岩机理。

3.1截齿破岩过程中的岩石裂纹演化

图7描述了双截齿钻进岩层的裂纹演化过程。结果表明，两截齿侵入时间0.1 s时，齿尖下方产生裂纹，但两裂纹并无影响；侵入时间0.3 s时，截齿侵深逐渐增大，齿尖下的裂纹扩展延伸成较大的裂纹区域；侵入时间0.8 s时，岩石表面的裂纹相交并开始贯通，岩片开始形成；随着侵入时间增大至2.0 s，内部裂纹搭接成片，且延伸的区域更大。双截齿侵入岩石的裂纹演化是从表面至内部，最终形成裂纹的全贯通，表明实际多截齿侵入过程中，由于截齿间相互作用，会形成更大的破碎体积，也提高了最终的破岩效率。

3.2截齿破岩过程中的力学响应特征

3.2.1 截齿旋挖过程中的力-位移演化特征

图8给出了双截齿侵入过程中的竖向侵入力-侵深、切向力-切割位移曲线。结果显示，侵入力随侵深的增加而增大，侵深为3.8、7.5、13 mm时，法向力突然下降，且下降点对应的侵深间隔越来越小，说明截齿侵入岩石的过程中产生初始裂纹，岩石突然破碎，截齿出现跳跃性的侵入。当侵入力增加时，裂纹扩展加快，岩块破碎速率增加，截齿跳跃性的侵入频率增大。根据切向力与切割位移的关系曲线可知，切向力随位移呈循环式波动，主要在于岩石受到扭矩产生的切削作用时，岩块出现较大体积的剥离，当切向力达到临界值时，截齿突然跃进，岩块断裂剥离，切向力快速下降，截齿继续向前接触新岩面，产生切向力突然增大的现象，如此跃进-接触-跃进循环往复，形成旋挖钻进的破岩过程。

3.2.2 截齿钻进中的岩石应力及应变分布

图9给出了不同时刻双截齿钻进的岩石应力分布云图，可分为4个区域：1）弹性区（最外层深蓝色区域）：岩石受力最小，未达到岩石屈服强度，弹性变形阶段。2）损伤区（浅蓝色区域）：潜在裂纹扩展区与弹性区之间，岩石受到截齿传递的破岩力，当达到岩石的屈服强度，岩石损伤。3）裂纹扩展区（绿色区域）：位于损伤区域的上方，岩石应力一旦超过屈服强度，裂纹扩展；当截齿经过该区域，冲击压力突然消失，裂纹在拉应力作用下沿半球形表面扩展，直至扩展到岩石表面，形成一个半球形的潜在破碎区域；该区域随钻头的旋转切削而剥落，产生较大块状的岩屑，形成破碎坑。4）破碎区（红色区域）：此区域与截齿齿尖直接接触，齿尖处应力集中，最易也最先达到岩石强度极限而破碎。

图9（a）显示，截齒钻进0.3 s时，两截齿的应力区域开始重叠，两齿尖周围的塑性区越来越大；随着侵入时间增至2.0 s，塑性区及超过极限强度的岩块越来越多，表明破坏区域越来越大。对比图9（b）的等效塑性应变分布，钻进0.3 s时，较大的塑性应变主要出现在齿尖，当截齿钻进2.0 s时，塑性应变越来越大，进入塑性区的岩石连接成片，形成较大的破碎坑体积。由此可见，截齿钻进中的岩体塑性区与塑性变形分布与其裂纹演化规律一致，表明了三维数值模拟的旋挖钻机力学响应特征是可以揭示截齿破岩机理的。

4不同截齿布置的旋挖钻机破岩分析

4.1不同截齿倾角的破岩力特征

根据前述的侵入力及切削力计算模型，破岩力为两力之和。考虑不同截齿倾角的破岩分析，三维数值模拟得到截齿破岩力随钻进深度的变化，如图11所示。结果表明，截齿倾角增大将导致破岩力呈非线性增大。但是，破岩力主要表征截齿钻进中的侵入力和切向力大小，对破岩效率的判断不够。为此，引入截齿破岩能耗的概念——破碎比功，评价不同截齿倾角下的破碎效率，可用来确定最优截齿倾角。破碎比功的计算结果如图12所示，显示截齿倾角在0～60°范围内，破碎比功先减小至最小值，然后逐渐增大，可见截齿破岩中存在最优截齿倾角，当截齿倾角大约30°时，破碎比功最小，对应的截齿破岩效率最高。

4.2不同截齿偏斜角的破岩力特征

图13（a）给出了不同截齿偏斜角的破岩力变化，表明截齿侵入过程中的破岩力随侵深增加呈波动式增大。同一侵深时，侵入力随偏斜角增大而增大，当截齿偏斜角45°时，其破岩力的变化趋势与偏斜角0°～35°有明显差异，表明偏斜角45°时的截齿破岩出现异常，实际旋挖钻机设计中需要避免偏斜角45°。如图13（b）所示的切削力随切削位移循环波动，表明不同偏斜角时的切削力波动频率不同，偏斜角 0°、25°和45°的波动频率较小，幅值较大，说明这些角度下的岩块破碎体积较大，破岩速率较小；而偏斜角15°和35°时的波动频率较大，幅值较小，此时对应的破碎岩块体积较小，而破岩速率较高。

另外，图14所示的不同偏斜角截齿破岩效率表明，截齿偏斜角0～45°的破碎比功先减小，当偏斜角25°时达到极小值，随后逐渐增大。可见，当截齿偏斜角25°时，破碎比功最小，即偏斜角25°对应的截齿破岩效率最高。

5旋挖机破岩的截齿布置优化分析

不同截齿布置方式（排列方式、截齿偏斜角、截齿间距等）的破岩效率差异显著。实际旋挖钻机的成孔中，会遭遇不同地层环境，其破岩效率也将不同。考虑表3的四类地层力学参数，基于三维旋挖钻进数值模型，分析对应工况的破碎比功，并提出优化建议。

5. 1不同地层破岩的最优截齿倾角

图15给出了不同截齿倾角钻进不同地层的破碎比功变化规律。结果表明，截齿倾角相同、地层由软到硬时，破碎比功的数值变化较大，软岩对应的破岩比功最小，而硬岩对应的破碎比功最大，软岩和较软岩的破碎比功在0～1 000 kJ/m³，较硬和硬岩的破碎比功在1 000 ～3 000 kJ/m³，说明某一特定旋挖机施工时，钻进硬岩地层消耗的能量大，破岩难度相对大。对某一类地层而言，破碎比功均先减小后增大，根据最小破碎比功对应最优截齿倾角，可得到不同地层即硬岩、较硬岩、较软岩、软岩的最优截齿倾角32°、30°、29°和27°，截齿破岩中的最优截齿倾角约30°左右。

由此可见，不同地层的截齿破岩均出现最小破碎比功，阐明不同地层的旋挖钻进存在最优的截齿倾角。实际旋挖钻机截齿的安装设计，需结合地层特性选择合适的截齿倾角，以提高破岩效率。

5. 2不同地层破岩的最优截齿偏斜角

图16给出了不同截齿偏斜角的旋挖钻机钻进不同地层的破碎比功曲线。由图可知，旋挖钻进某一类地层时，截齿偏斜角增大，破碎比功先减小后增大，说明破岩过程中存在最小破碎比功，旋挖钻进不同地层时，均存在最优偏斜角。当截齿偏斜角相同时，破碎比功由软岩、较软岩、较硬岩、硬岩地层呈现跳跃性增大，各地层的破碎比功数值无交叉，说明地层类型对截齿破岩的破碎比功影响大，即地层越坚硬，旋挖钻进的难度越大，旋挖效率越低。另外，截齿钻进软岩地层时的最优偏斜角最大，主要在于软岩地层强度较低，截齿随钻头旋转时，受到水平面上的扭矩较小，合力中心线在钻头切线方向的夹角较大，截齿轴线与合力中心线重合，则偏斜角较大；而破碎硬岩地层时，受到水平方向的扭矩较大，合力中心线与切线方向的夹角减小，故偏斜角较小。根据图16可得，不同地层即硬岩、较硬岩、较软岩、软岩的最优偏斜角为15°、25°、33°和38°，表明了不同地层的旋挖钻进设计中需要考虑最优的截齿偏斜角，以提高破岩效率。

5. 3不同地层破岩的最优截齿间距

图17给出了不同截齿间距的旋挖钻机钻进不同地层的破碎比功曲线，同样存在最小破碎比功和最优的截齿间距。图形显示，当截齿为同一间距时，破碎比功由软岩、较软岩、较硬岩、硬岩地层呈现跳跃性增大，说明地层类型对旋挖钻进中的截齿破岩破碎比功影响大，即地层越坚硬，旋挖钻进的难度越大，旋挖效率越低。另外，当地层类型一定时，截齿间距增大，破碎比功先减小后增大，存在极小值，即截齿破岩存在最优截齿间距。由图可得，硬岩、较硬岩、较软岩、软岩的最优截齿间距分别为60、68、80、90 mm，表明地层硬度增大，最优截齿间距越小，主要在于地层越硬，截齿侵入后的岩体裂纹扩展速度慢，若截齿间距过大，截齿下的岩体裂纹扩展延伸难度大，只有当截齿间距相对较小时，硬岩裂纹才能快速扩展搭接形成大的岩片。由此可知，相对较软地层的钻进过程，要达到同样的破碎比功，硬岩钻进需要安装更多的截齿，才能保证相同的能量消耗中切割体积相同的岩体，但过小的截齿间距，会出现截齿下裂纹交互频繁，截齿向下过度破碎岩体而产生更大的破碎比功，此时形成的岩片體积将过小，破岩效率反而较低。因此，当地层类型确定后，选择合理的截齿间距才能获得更优的破碎比功。

6结  论

旋挖钻机的成孔优势备受关注，实际施工中的最优破岩效率是关键。文中结合理论分析，验证截齿破岩三维数值模型的可行性，模拟旋挖钻机截齿在动力头压力及扭矩下的破岩过程，探讨截齿破岩的力学响应及裂纹演化特征，分析不同截齿布置的破岩力变化规律，研究不同截齿布置在不同地层中的破岩效率，并给出优化建议。主要结论如下：

1）结合截齿破岩的理论公式，分析截齿破岩三维数值模拟的侵入及切削过程，验证数值模型的可行性。通过双截齿破岩中的岩体力学响应及裂纹演化特征，解释钻机破岩机理。

2）分析不同截齿布置的旋挖钻机破岩力特征，表明截齿倾角增大时，破岩力呈非线性增大；偏斜角增大，破岩力呈现不同的波动频率和幅值，可根据频率可定性分析破碎岩体的体积及破岩速率。

3）截齿布置方式对不同地层的破岩效率影响较大。当截齿倾角相同时，由软到硬地层的破碎比功变化较大，软岩的破岩比功最小，硬岩破碎比功最大，对某一类地层，破碎比功均先减小后增大；截齿偏斜角相同时，破碎比功由软岩、较软岩、较硬岩、硬岩地层呈现跳跃性增大，某一地层旋挖钻进时，截齿偏斜角增大，破碎比功先减小后增大；截齿间距相同时，破碎比功由软岩、较软岩、较硬岩、硬岩地层呈现跳跃性增大，即地层越坚硬，旋挖效率越低，当地层类型一定时，截齿间距增大，破碎比功先减小至最小值后增大，说明存在最优截齿布置使得旋挖钻进效率最高。

由此可见，实际旋挖钻机施工过程中，不同地层的钻孔需要考虑赋存环境与截齿布置的协同作用，才能不断优化截齿设计以获得更高的破岩效率，并减少钻头的磨损。

参考文献

［1］  黎中银， 夏柏如， 吴方晓. 旋挖钻机高效入岩机理及其工程应用[J]. 中国公路学报， 2009， 22（3）： 121-126.

Li Z Y， Xia B R， Wu F X. Mechanism of efficient rock cracking and its engineering application of rotary drilling rig[J]. China Journal of Highway and Transport， 2009， 22（3）： 121-126.（in Chinese）

［2］  Jonak J， Podgórski J. Mathematical model and results of rock cutting modeling[J]. Journal of Mining Science， 2001， 37（6）： 615-618.

［3］  Evans I. A theory of the cutting force for point-attack picks[J]. International Journal of Mining Engineering， 1984， 2（1）： 63-71.

［4］  劉春生， 靳立红. 基于截槽非对称条件镐形截齿的截割力学模型[J]. 煤炭学报， 2009， 34（7）： 983-987.

Liu C S， Jin L H. The cut mechanical model of pick-shaped cutter under conditions of dissymmetrical slotting[J]. Journal of China Coal Society， 2009， 34（7）： 983-987.（in Chinese）

［5］  Gao K D， Du C L， Jiang H X， et al. A theoretical model for predicting the Peak Cutting Force of conical picks[J]. Frattura Ed Integrità Strutturale， 2013， 8（27）： 43-52.

［6］  刘晋霞， 马超， 曾庆良， 等. 镐型截齿截割煤岩过程的截割力研究[J]. 煤炭学报， 2017， 42（5）： 1325-1330.

Liu J X， Ma C， Zeng Q L， et al. Research on cutting force of conical pick in cutting coal process[J]. Journal of China Coal Society， 2017， 42（5）： 1325-1330.（in Chinese）

［7］  蔡灿， 伍开松， 廉栋， 等. 单齿冲击作用下破岩机制分析[J]. 岩土力学， 2015， 36（6）： 1659-1666， 1675.

Cai C， Wu K S， Lian D， et al. Study of rock-breaking mechanism under single-tooth impact[J]. Rock and Soil Mechanics， 2015， 36（6）： 1659-1666， 1675.（in Chinese）

［8］  赵伏军， 谢世勇， 潘建忠， 等. 动静组合载荷作用下岩石破碎数值模拟及试验研究[J]. 岩土工程学报， 2011， 33（8）： 1290-1295.

Zhao F J， Xie S Y， Pan J Z， et al. Numerical simulation and experimental investigation on rock fragmentation under combined dynamic and static loading[J]. Chinese Journal of Geotechnical Engineering， 2011， 33（8）： 1290-1295.（in Chinese）

［9］  Geng D X， Zhang D Y， Xu Y G， et al. Effect of speed ratio in edge routing of carbon fiber-reinforced plastics by rotary ultrasonic elliptical machining[J]. Journal of Reinforced Plastics and Composites， 2015， 34（21）： 1779-1790.

［10］  刘春生， 李德根. 不同截割状态下镐型截齿侧向力的实验与理论模型[J]. 煤炭学报， 2016， 41（9）： 2359-2366.

Liu C S， Li D G. Experimental research and theoretical model on lateral force of conical pick under different cutting conditions[J]. Journal of China Coal Society， 2016， 41（9）： 2359-2366.（in Chinese）

［11］  Li Z， Zhang D Y， Jiang X G， et al. Study on rotary ultrasonic-assisted drilling of titanium alloys （Ti₆Al₄V） using 8-facet drill under no cooling condition[J]. The International Journal of Advanced Manufacturing Technology， 2017， 90（9）： 3249-3264.

［12］  戴珊珊. 基于ABAQUS模擬镐形截齿截割脆性煤岩[J]. 煤矿机械， 2012， 33（5）： 46-48.

Dai S S. Simulation of brittle coal cutting by conical pick based on ABAQUS[J]. Coal Mine Machinery， 2012， 33（5）： 46-48.（in Chinese）

［13］  江红祥， 杜长龙， 刘送永， 等. 基于断裂力学的岩石切削数值分析探讨[J]. 岩土力学， 2013， 34（4）： 1179-1184.

Jiang H X， Du C L， Liu S Y， et al. Numerical analysis of rock cutting based on fracture mechanics[J]. Rock and Soil Mechanics， 2013， 34（4）： 1179-1184.（in Chinese）

［14］  Saksala T， Gomon D， Hokka M， et al. Numerical and experimental study of percussive drilling with a triple-button bit on Kuru granite[J]. International Journal of Impact Engineering， 2014， 72： 56-66.

［15］  Fourmeau M， Kane A， Hokka M Experimental and numerical study of drill bit drop tests on Kuru granite[J]. Philosophical Transactions of the Royal Society of London， A 375： 20160176. http：//dx.doi.org/10.1098/rsta.2016.0176.

［16］  周子龙， 刘玉良， 赵云龙， 等. 不同围压与不同截齿侵入角作用下镐形截齿破岩数值模拟分析[J]. 世界科技研究与发展， 2016， 38（3）： 598-603.

Zhou Z L， Liu Y L， Zhao Y L， et al. Numerical analysis on breaking rock by pick-shaped cutter at different confining pressure and invasion angle[J]. World Sci-Tech R & D， 2016， 38（3）： 598-603.（in Chinese）

（编辑  陈移峰）