考虑扭转速度预估的大型风电机组传动链扭振抑制方法

任坤涛 朱才朝 谭建军 宋朝省 王叶

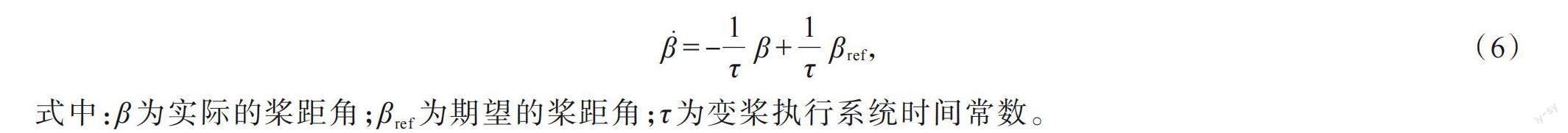
doi： 10.11835/j.issn.1000-582X.2022.009

收稿日期：2021-12-28

網络出版日期：2022-04-17

基金项目：重庆市自然科学基金资助项目（cstc2020jcyj-msxmX0710）；中央高校基本科研业务费（2020CDJ-LHSS-008、2021CDJCGJ008） 资助。

Foundation：Supported by the General Project of Chongqing Natural Science Foundation （cstc2020jcyj-msxmX0710）， and the Fundamental Research Funds for the Central Universities （2020CDJ-LHSS-008， 2021CDJCGJ008）.

作者简介：任坤涛（1996—），男，硕士研究生，主要从事风电机组传动链扭振控制策略研究，（E-mail）986453607@qq.com。

通信作者：朱才朝，男，教授，博士生导师，（E-mail）cczhu@cqu.edu.cn。

摘要：大型风电机组传动链转动惯量大，在随机风速作用下低频扭振风险高，而传统基于确定扭转速度控制目标的传动链扭振控制方法未考虑因测量设备引起的随机测量噪声对扭转速度的影响，可能导致控制性能下降。针对扭转速度测量不确定性，提出了大型风电机组传动链扭振自抗扰控制方法，设计了KF-ADRC扭振控制器，通过卡尔曼滤波动态估计传动链扭转速度，并以扭转速度为零作为ADRC控制目标，控制发电机电磁转矩，抑制传动链低频扭振。研究结果表明：当常规的扭振控制器输入信号存在随机测量噪声时，会显著降低其对传动链低频扭振的抑制性能，而KF-ADRC扭振控制器在输入信号存在测量噪声时可有效预估传动链扭转速度，较好地实现了传动链低频扭振抑制效果。

关键词：风电机组；传动链；低频扭振；自抗扰控制；卡尔曼滤波

中图分类号：TH11          文献标志码：A      文章编号：1000-582X（2023）09-001-12

Torsional vibration suppression method of large-scale wind turbine drivetrain considering torsional speed prediction

REN Kuntao¹， ZHU Caichao¹， TAN Jianjun¹， SONG Caosheng¹， WANG Ye²

（1. State Key Laboratory for Mechanical Transmissions， Chongqing University， Chongqing 400044， P. R. China; 2. CSIC（Chongqing） Haizhuang Windpower Equipment Co.， Chongqing 401122， P. R. China）

Abstract： The drivetrain of high-power wind turbines has a large moment of inertia， resulting in a high risk of low-frequency torsional vibration when subjected to random wind speeds. The traditional torsional vibration control method for the drivetrain based on the determination of the torsional speed control target fails to consider the influence of the random measurement noise introduced by the measurement equipment on the torsional speed. This oversight can lead to a decrease in control performance. To address the uncertainty associated with torsion speed measurement， this paper proposed an active disturbance rejection control method for torsional vibration of large-scale wind turbine drivetrain. A KF-ADRC torsional vibration controller was designed which dynamically estimated the torsion speed of drivetrain using a Kalman filter. The ADRC control target was set as zero torsion speed to regulate the electromagnetic torque of the generator and suppress low-frequency torsional vibration in the drivetrain. The research results show that when the input signal of the conventional torsional vibration controller has random measurement noise， it will significantly reduce its performance. In contrast， the KF-ADRC torsional vibration controller can effectively predict the drivetrains torsional speed and achieve superior suppression of the low-frequency torsional vibration in the drivetrain.

Keywords： wind turbine; drivetrain; low-frequency torsional vibration; active disturbance rejection control; Kalman filter

风电机组是目前最有效开发风资源的重大工程装备之一。为进一步降低风资源开发成本，风电机组正朝着大功率、巨型化发展，这也导致了风电机组部件大惯量、柔性化，增大了风电机组传动链低频扭振风险^[1?3]，容易造成系统部件疲劳失效，同时还可能造成电力系统振荡^[4]，威胁电网运行安全，因此开展风电机组传动链扭振控制研究具有重要意义。

近年来，国内外学者针对传动链扭振控制开展了大量研究。Mandic等^[5]通过带通滤波器提取高速轴转速中的扭振信息，由发电机进行补偿，在工程中已被广泛使用；Licari等^[6]针对风电机组传动链考虑被控系统参数变化提出了基于模型的控制方法，提高了系统的鲁棒性；Zhu等^[7]針对风电机组传动链考虑模型不确定性提出了基于扰动观测器的控制方法，具有良好的降噪效果与低频特性；贾锋等^[8]针对风电机组传动链考虑带通滤波器引起的系统低频特性改变提出了受迫阻尼重塑方法，有效地降低了轴系宽频受迫振动；由于滑膜控制具有良好的抗扰鲁棒性，Fateh等^[9]针对风电机组传动链提出了基于高阶滑膜的控制方法，相比虚拟惯性控制具有更快响应；Karunanayake等^[10]针对风电机组传动链提出了滑膜控制方法来减轻传动链扭振；Liu等^[11]针对风电机组传动链提出了一种基于扭转角度与速度的阻尼、刚度补偿控制方法。上述研究为传动链扭振抑制提供了有效指导，但均假定系统参数已知，而在实际控制中部分系统参数难以获取，具有一定的工程应用局限性。

为此，国内外部分学者针对模型参数难以准确获取的风电机组传动链扭振抑制问题，将ADRC引入到传动链扭振抑制中，开展了ADRC对传动链扭振抑制的研究。自抗扰控制器（active disturbance rejection control， ADRC）^[12?13]由扩张状态观测器（extend state observer， ESO）、非线性状态误差反馈控制率（nonlinear state error feedback law， NLSEF）、跟踪微分器（tracking differentiator， TD）组成，ADRC不依赖精确的数学模型，由ESO估计控制过程的不确定因素，作为前馈进行补偿，降低了控制器实现难度。姚兴佳等^[14]利用ADRC以风电机组传动链扭转速度为目标降低了传动链扭振；葛帅帅等^[15]利用ADRC方法以采煤机截割传动系统扭转速度为目标降低了传动系统的动载荷；Ren等^[16]提出了具有制动器饱和的ADRC控制方法，以传动链扭转角度为控制目标降低了传动链载荷；Madonski等^[17]针对大不确定扭转系统的振动抑制与追踪问题提出了基于误差的ADRC控制方法，解决了谐波扰动下的振动抑制问题。上述研究虽然在一定程度上抑制了传动链扭振，但仍需要精准地扭转速度作为ADRC输入，忽略了因测量设备引入的随机测量噪声的影响，会影响控制器的实际应用性能。

针对扭转速度测量不确定因素，提出了KF-ADRC扭振控制器，通过卡尔曼滤波动态估计传动链扭转速度，以扭转速度为零作为ADRC控制目标，控制发电机电磁转矩，对比分析了当输入信号存在随机测量噪声时KF-ADRC对传动链扭振的抑制效果。

1风电机组运行原理

图1为风电机组主要组成部分，包括空气动力学系统、机械系统、发电机系统和控制系统^[18]。空气动力学系统捕获风能并在低速轴产生转矩，通过机械系统进行增速降扭，将能量传递到发电机系统并进行发电；控制系统通过改变发电机输出电磁转矩和调整桨距角保证风电机组能够最大化捕获风能、维持风电机组安全运行。

2风电机组传动链扭振控制策略

2.1风电机组传动链系统模型

当风扫掠过风轮时，风轮获得的功率P^[20]为

风电机组为典型的气-弹-水-控耦合系统，整机模型计算成本高，因此控制系统的有效性验证通常通过简化模型验证，主要包括单质量块模型、两质量块模型和多质量块模型^[21-22]。文献[23]表明风电机组系统两质量块模型与风电机组专业仿真软件FAST整机模型响应的匹配度较好，因此采用两质量块模型验证控制策略的有效性。如图3所示，采用集中质量法，将叶片与轮毂转动惯量等效为风轮端转动惯量，发电机转子转动惯量等效为发电机端转动惯量，考虑传动链扭转自由度，忽略其内部去损耗，其动力学方程为

2.2基于卡尔曼滤波的传动链扭转速度预估

在实际工程中，传动链扭转速度的测量需通过测量高速轴转速、低速轴转速、齿轮箱传动比，由式（4）计算得到，每个数据的测量都会引入一定的测量噪声，使得计算的传动链扭转速度受到3个数据叠加的测量噪声影响，同时扭转速度由于自身数量级较小，更易受到测量噪声影响造成扭转速度测量值相比于真实值产生较大偏差^[7?8]，为此引入卡尔曼滤波器滤除过程噪声与测量噪声，对传动链扭转速度进行最优估计。

根据式（3）和式（4），风电机组传动链动力学方程可写成状态空间方程为

根据零阶保持器将式（7）进行离散化

为使估计值与真实值误差最小，需求解最小估计误差协方差矩阵，为

根据估计状态值与实际值，计算卡尔曼增益

通过卡尔曼增益对系统进行校正，对状态值进行后验估计并更新误差协方差矩阵

2.3风电机组传动链ADRC扭振控制器设计

图5为风电机组传动链KF-ADRC扭振控制框图，其中KF-ADRC的输入信号包括发电机电磁转矩、气动转矩及高速轴转速；ADRC的输入信号为传动链扭转速度。

3结果讨论与分析

以某型兆瓦级漂浮式风电机组传动链为仿真对象，参数如表1所示。图6为仿真所用湍流风，利用Turbsim^[28]生成100 s 均值为16 m/s的A级湍流风，利用Matlab/Simulink进行仿真，观察KF-ADRC扭振控制器在发电机电磁转矩、气动转矩和高速轴转速3个输入信号均存在测量噪声情况下对传动链扭振的抑制效果。

3.1传动链扭转速度预估

图7为無测量噪声下卡尔曼滤波对传动链扭转速度预估效果。从图中可以看出，在湍流风扰动下，预估值与真实值吻合较好，表明卡尔曼滤波对传动链扭转速度具有良好的预估效果。

图8为当3个输入信号均存在标准测量噪声或大噪声干扰时卡尔曼滤波对传动链扭转速度预估的效果。从图中可以看出，卡尔曼滤波在测量噪声干扰下对传动链扭转速度预估精度有所降低，并且随着测量噪声增加，预估效果逐渐降低，但整体上卡尔曼滤波仍具有良好的估计效果。

图9为输入信号分别在无噪声、存在标准噪声以及大噪声情况下卡尔曼滤波器对传动链扭转速度的预估精度对比。从图中可以看出，随着测量噪声的增加，局部精度有所下降，但总体精度几乎不变。

3.2传动链KF-ADRC扭振控制

图10为当输入信号存在大噪声情况下的传动链KF-ADRC扭振控制器性能。其中，Baseline代表无扭振控制器；ADRC代表没有卡尔曼滤波器，仅有ADRC控制器。从图中可以看出，在输入信号存在大噪声情况下，仅使用ADRC控制会加剧低速轴转矩与功率波动，以及增加高速轴转速波动，而采用KF-ADRC扭振控制可以有效地减少低速轴转矩、高速轴转速波动。文献[30?32]对ADRC进行了理论仿真和试验验证，发现ADRC的性能会受到测量噪声的影响，对输入信号的追踪能力越强，越容易受到测量噪声的影响，这是因为当输入信号存在测量噪声时，会导致ADRC中的ESO对输入信号、输入信号微分、总扰动的估计出现一定偏差，降低ADRC的控制性能；而KF-ADRC可以有效预估传动链最优扭转速度，降低输入信号中测量噪声的影响。

表2为KF-ADRC作用下功率与低速轴转矩的数据统计。从表2中可以看出，在扭振控制器的输入信号存在大噪声的情况下，采用KF-ADRC扭振控制可以使传动链低速轴转矩标准差相比于无扭振控制器降低25.4%，但功率波动略有增加，其均值基本不变。KF-ADRC可有效降低传动系统扭振，但是过于追求传动系统的平稳性可能会加剧发电功率波动，因此控制系统的设计需要综合考虑传动系统降载与功率稳定性的匹配。

为了进一步分析KF-ADRC扭振控制器对输入信号中测量噪声的敏感性，分别对比了当输入信号存在标准噪声与大噪声时，KF-ADRC控制器、ADRC控制器相比于未加扭振控制器的传动链低速轴转矩和功率变化情况，如表3所示。其中，负号代表低速轴转矩标准差或功率标准差得到了降低，正号代表增加。从表中可以看出，当输入信号测量噪声水平为标准噪声时，KF-ADRC较无扭振控制器低速轴转矩标准差降低了25.4%，较ADRC控制具有更好的扭振抑制效果与较低的功率波动；当输入信号测量噪声水平为大噪声时，KF-ADRC扭振抑制效果几乎不变，而仅使用ADRC会增加传动链扭振，表明KF-ADRC对输入信号中存在的随机测量噪声具有很好的适用性。

4结论

针对测量噪声引起的扭转速度测量不确定性，提出了KF-ADRC扭振控制方法，分析了KF-ADRC的输入信号在不同测量噪声影响下其对传动链低频扭振的抑制效果，主要结论如下：

1）当常规的传动链扭振控制器输入信号存在测量噪声时，会降低其扭振抑制性能，并且随着测量噪声的增大，对传动链的扭振抑制会出现不降反增的现象。

2）KF-ADRC扭振控制器在输入信号存在不同测量噪声时可以有效预估传动链扭转速度，抑制传动链扭振，相比于无扭振控制器时传动链低速轴转矩标准差降低了25.4%，且对功率的影响较小。

参考文献

［1］  Rahman M， Ong Z C， Chong W T， et al. Performance enhancement of wind turbine systems with vibration control： a review[J]. Renewable and Sustainable Energy Reviews， 2015， 51： 43-54.

［2］  李辉， 胡玉， 柴兆森， 等. 随机风载荷对双馈风电机组轴系扭振响应分析[J]. 太阳能学报， 2020， 41（5）： 174-181.

Li H， Hu Y， Chai Z S， et al. Analysis on shaft torsional vibration responses of doubly fed induction generators under stochastic wind load[J]. Acta Energiae Solaris Sinica， 2020， 41（5）： 174-181.（in Chinese）

［3］  秦大同， 鲁迪， 陈锐博， 等. 随机风速下风电传动系统机电耦合动态特性分析[J]. 太阳能学报， 2020， 41（11）： 326-333.

Qin D T， Lu D， Chen R B， et al. Electromechanical coupling dynamic characteristic analysis of wind turbine transmission system under random wind speed[J]. Acta Energiae Solaris Sinica， 2020， 41（11）： 326-333.（in Chinese）

［4］  姚骏， 曾欣， 李嘉伟. 并网双馈感应风电系统轴系振荡特性[J]. 电工技术学报， 2017， 32（6）： 123-135.

Yao J， Zeng X， Li J W. Shaft oscillation characteristics of grid-connected doubly-fed induction generator-based wind power generation system[J]. Transactions of China Electrotechnical Society， 2017， 32（6）： 123-135.（in Chinese）

［5］  Mandic G， Nasiri A， Muljadi E， et al. Active torque control for gearbox load reduction in a variable-speed wind turbine[J]. IEEE Transactions on Industry Applications， 2012， 48（6）： 2424-2432.

［6］  Licari J， Ugalde-Loo C E， Ekanayake J B， et al. Damping of torsional vibrations in a variable-speed wind turbine[J]. IEEE Transactions on Energy Conversion， 2013， 28（1）： 172-180.

［7］  Zhu H Z， Yoshida S. Disturbance observer-based torsional vibration damper for variable-speed wind turbines[J]. IFAC Journal of Systems and Control， 2020， 14： 100112.

［8］  贾锋， 陈雷， 符杨， 等. 湍流激励下风电轴系的宽频受迫扭振及其抑制方法[J]. 中国电机工程学报， 2021， 41（19）：6591-6601.

Jia F， Chen L， Fu Y， et al. The forced wide frequency-band torsional vibration of WECS drive train under turbulence wind and its suppression method[J]. Proceedings of the CSEE，2021，41（19）：6591-6601.（in Chinese）

［9］  Fateh F， White W N， Gruenbacher D. Torsional vibrations mitigation in the drivetrain of DFIG-based grid-connected wind turbine[J]. IEEE Transactions on Industry Applications， 2017， 53（6）： 5760-5767.

［10］  Karunanayake C， Ravishankar J， Dong Z Y. A novel torsional vibration mitigation strategy for DFIG based wind turbines[C]//2019 7th International Conference on Smart Grid （icSmartGrid）. IEEE， 2020： 27-32.

［11］  Liu J， Zhou F， Zhao C， et al. Mechanism analysis and suppression strategy research on permanent magnet synchronous generator wind turbine torsional vibration[J]. ISA Transactions， 2019， 92： 118-133.

［12］  韓京清. 自抗扰控制器及其应用[J]. 控制与决策， 1998， 13（1）： 19-23.

Han J Q. Auto-disturbances-rejection controller and its applications[J]. Control and Decision， 1998， 13（1）： 19-23.（in Chinese）

［13］  Huang Y， Han J Q. Analysis and design for the second order nonlinear continuous extended states observer[J]. Chinese Science Bulletin， 2000， 45（21）： 1938-1944.

［14］  姚興佳， 王晓东， 单光坤， 等. 双馈风电机组传动系统扭振抑制自抗扰控制[J]. 电工技术学报， 2012， 27（1）： 136-141.

Yao X J， Wang X D， Shan G K， et al. Torque vibration active disturbance rejection control of double-fed wind turbine drive train[J]. Transactions of China Electrotechnical Society， 2012， 27（1）： 136-141.（in Chinese）

［15］  葛帅帅， 秦大同， 胡明辉， 等. 基于自抗扰转矩补偿的采煤机截割传动系统动载荷主动控制[J]. 机械工程学报， 2018， 54（15）： 31-40.

Ge S S， Qin D T， Hu M H， et al. Active control on dynamic loads of the drum shearer cutting transmission system based on active disturbance rejection torque compensation[J]. Journal of Mechanical Engineering， 2018， 54（15）： 31-40.（in Chinese）

［16］  Ren L N， Mao C H， Song Z Y， et al. Study on active disturbance rejection control with actuator saturation to reduce the load of a driving chain in wind turbines[J]. Renewable Energy， 2019， 133： 268-274.

［17］  Madonski R， Ramirez-Neria M， Stankovi? M， et al. On vibration suppression and trajectory tracking in largely uncertain torsional system： an error-based ADRC approach[J]. Mechanical Systems and Signal Processing， 2019， 134： 106300.

［18］  Pourseif T， Afzalian A. Pitch angle control of wind turbine systems in cold weather conditions using μ robust controller[J]. International Journal of Energy and Environmental Engineering， 2017， 8（3）： 197-207.

［19］  Tomás Rodríguez M， Santos M. Modelado y control de turbinas eólicas marinas flotantes[J]. Revista Iberoamericana De Automática e Informática Industrial， 2019， 16（4）： 381-390.

［20］  Abouzeid S I， Guo Y， Zhang H C. A frequency response strategy for variable speed wind turbine based on a dynamic inertial response and tip-speed ratio control[J]. Electrical Engineering， 2019， 101（1）： 35-44.

［21］  Muyeen S M， Ali M H， Takahashi R， et al. Comparative study on transient stability analysis of wind turbine generator system using different drive train models[J]. IET Renewable Power Generation， 2007， 1（2）： 131.

［22］  Tabesh A， Iravani R. Transient behavior of a fixed-speed grid-connected wind farm[C]// International Conference on Power Systems Transients. Montreal， Canada， IEEE， 2005： 1-5.

［23］  Azizi A， Nourisola H， Shoja-Majidabad S. Fault tolerant control of wind turbines with an adaptive output feedback sliding mode controller[J]. Renewable Energy， 2019， 135： 55-65.

［24］  Smilden E， Horn J T H， S?rensen A J， et al. Reduced order model for control applications in offshore wind turbines[J]. IFAC-PapersOnLine， 2016， 49（23）： 386-393.

［25］  陈旭， 朱才朝， 宋朝省， 等. 紧急停机工况下风力发电机系统动态特性分析[J]. 机械工程学报， 2019， 55（5）： 82-88.

Chen X， Zhu C C， Song C S， et al. Dynamic characteristics analysis of wind turbine under emergency shutdown events[J]. Journal of Mechanical Engineering， 2019， 55（5）： 82-88.（in Chinese）

［26］  王诗琪， 杜雪松， 朱才朝， 等. 海上浮式风电机组变桨距自抗扰控制策略研究[J]. 重庆大学学报， 2022， 45（10）：25-37.

Wang S Q， Du X S， Zhu C C， et al. Research on adrc for pitch control of offshore floating wind turbine[J]. Journal of Chongqing University， 2022， 45（10）：25-37. （in Chinese）

［27］  陈文英， 褚福磊， 阎绍泽. 基于自适应遗传算法分步优化设计智能桁架结构自抗扰振动控制器[J]. 机械工程学报， 2010， 46（7）： 74-81.

Chen W Y， Chu F L， Yan S Z. Stepwise optimal design of active disturbances rejection vibration controller for intelligent truss structure based on adaptive genetic algorithm[J]. Journal of Mechanical Engineering， 2010， 46（7）： 74-81.（in Chinese）

［28］  Wang X， Gao W Z， Scholbrock A， et al. Evaluation of different inertial control methods for variable-speed wind turbines simulated by fatigue， aerodynamic， structures and turbulence （FAST）[J]. IET Renewable Power Generation， 2017， 11（12）： 1534-1544.

［29］  Branlard E， Giardina D， Brown C S D. Augmented Kalman filter with a reduced mechanical model to estimate tower loads on a land-based wind turbine： a step towards digital-twin simulations[J]. Wind Energy Science， 2020， 5（3）： 1155-1167.

［30］  Li J， Xia Y Q， Qi X H， et al. On the necessity， scheme， and basis of the linear-nonlinear switching in active disturbance rejection control[J]. IEEE Transactions on Industrial Electronics， 2017， 64（2）： 1425-1435.

［31］  Zheng Q， Gao L Q， Gao Z Q. On validation of extended state observer through analysis and experimentation[J]. Journal of Dynamic Systems， Measurement， and Control， 2012， 134（2）： 024505.

［32］  Bai W Y， Xue W C， Huang Y， et al. On extended state based Kalman filter design for a class of nonlinear time-varying uncertain systems[J]. Science China Information Sciences， 2018， 61（4）： 042201.

（編辑  詹燕平）