显式拓扑优化的拉压杆模型自动提取方法

乔文正 袁维海 辜继明

doi：10.11835/j.issn.1000.582X.2023.09.008

收稿日期：2022-04-30

基金項目：国家自然科学基金资助项目（41807223， 12102002）；安徽省高校自然科学研究重点项目（KJ2020A0260）；吕梁市科技计划项目（2022RC24）。

Foundation：Supported by the National Natural Science Foundation of China （41807223， 12102002）， the Natonal Science Foundation Granted by Department of Education，Anhui Province （KJ2020A0260）， and Science and Technology Projects of Lyvliang City （2022RC24）.

作者简介：乔文正（1986—），男，博士研究生，主要从事结构工程和岩土工程研究，（E-mail）qiaowzh@llu.edu.cn。

通信作者：袁维海，男，副研究员，硕士生导师，（E-mail）yuanwh@hhu.edu.cn。

摘要：为了实现从显式拓扑优化到拉压杆模型的自然过渡，同时保持拓扑优化结构与拉压杆模型的拓扑一致性，以可移动变形组件拓扑优化为例，建立了显式拓扑优化拉压杆模型自动提取方法。该方法是计算机图形学和结构优化的结合，采用Voronoi骨架提取和形状优化，由骨架提取、框架提取和形状优化3部分构成。结果表明，该方法自动构建了受力合理且几何规则的拉压杆模型；Voronoi骨架提取从显式拓扑优化结构提取了光滑的中轴骨架；以类桁架指标为约束的形状优化实现了拉压杆模型从框架结构到桁架结构的质变。

关键词：显式拓扑优化；Voronoi图；骨架；拉压杆模型

中图分类号：TU375          文献标志码：A      文章编号：1000-582X（2023）09-066-12

Automatic extraction method of strut-and-tie models for explicit topology optimization

QIAO Wenzheng^1，2， YUAN Weihai²， GU Jiming³

（1. Department of Architecture， Lyuliang University， Lyuliang， Shanxi 033001， P. R. China; 2. College of Mechanics and Materials， Hohai University， Nanjing 211100， P. R. China; 3. School of Management Science and Engineering， Anhui University of Technology， Maanshan， Anhui 243002， P. R. China）

Abstract： To achieve the natural transition from explicit topology optimization to strut-and-tie models， while maintaining the topology consistency between the two， an automatic extraction method of strut-and-tie models using explicit topology optimization was developed. The proposed method is demonstrated using topology optimization based on moving morphable components as an example. It combines computer graphics and structural optimization techniques， employing skeleton extraction based on Voronoi diagram and shape optimization. The method consists of three main steps： skeleton extraction， frame extraction and shape optimization. The results show that the method can automatically generate strut-and-tie models with reasonable force distribution and regular geometry. The skeleton extraction based on Voronoi diagram extracts smooth and medial skeleton from the optimized structure obtained through explicit topology optimization. Shape optimization constrained by truss-like index realizes the qualitative change of strut-and-tie models from a frame structure to a truss structure.

Keywords： explicit topology optimization; Voronoi diagram; skeleton; strut-and-tie models

借助拓扑优化构建拉压杆模型（strut-and-tie models， STM）已经成为一种共识。根据优化模型的表达方式，拓扑优化可分为隐式拓扑优化和显式拓扑优化。隐式拓扑优化包括经典的固体各向同性惩罚方法（SIMP）和渐近结构优化方法（ESO）。显式拓扑优化是显示边界演化的一类高效拓扑优化方法。自2014年可移动变形（moving morphable components， MMC）拓扑优化方法^[1]提出以来，显式拓扑优化^[2?5]迎来了快速的发展。Bruggi^[6]成功地将SIMP方法应用于二维和三维构件拉压杆模型的研究。Du等^[7]在SIMP方法中引入双模量本构关系，提出了考虑拉压不同模量的拓扑优化方法，并成功应用于拉压杆模型中。Xia等^[8]提出了一种不同拓扑优化的拉压杆模型自动化评估方法。该方法采用桁架提取算法实现了从拓扑优化结果到桁架模型的自动化，并采用3个定量指标对STM进行评价。Xia等^[9]提出了由拓扑优化、拓扑提取和形状优化构成的二维STM拓扑优化构建方法，并采用非线性有限元评估STM的结构性能。此后，Xia等^[10]又研究了三维STM的SIMP构建方法。Liang等^[11-12]将性能优化方法成功应用于钢筋混凝土结构和预应力混凝土结构的拉压杆模型的研究。Almeida^[13]將光滑ESO方法用于拉压杆模型的研究，并与ESO方法在计算准确性和效率上进行了比较。刘霞等^[14]采用遗传ESO算法构建钢筋混凝土平面构件的拉压杆模型，并在此基础上进行配筋优化。Victoria等^[15]将考虑拉压不同模量的等值线拓扑优化方法用于拉压杆模型研究。Zhang等^[16]采用分离单元模型的遗传ESO方法对钢筋混凝土构件进行受力钢筋的布局优化，证实了该方法可以有效减少钢筋用量。Zhong等^[17]将微桁架单元的ESO方法应用于对带有洞口的缺口梁拉压杆模型研究，提出了由初步评估、详细评估和最终评估构成的一套评估体系。Zhong等^[18]将微桁架单元的ESO扩展到三维情况，通过后张拉锚固区、T形梁和箱形梁3个实例证明了该方法在构建三维STM的有效性和正确性。

基于拓扑优化的STM研究多集中在隐式拓扑优化。笔者^[19?20]研究了基于MMC拓扑优化的STM的有效性和高效性，探讨了STM的自动提取。作为类桁架的一般化，拉压杆模型的杆件应为二力杆件。然而，自动提取的STM往往并非桁架结构，受力形式与框架结构类似，称之为“框架结构”。此外，该框架结构在杆件平行性和对称性方面也较为欠缺。

从拓扑优化结果到拉压杆模型，要么人为因素多，随意性大，要么需要繁琐的手动操作。为了实现从拓扑优化结构到STM的自动化，借鉴Xia等^[8?10]的思路，建立由骨架提取、框架提取和形状优化构成的显式拓扑优化的拉压杆模型自动提取方法。骨架提取采用计算机图形学中的Voronoi骨架提取法。在形状优化中引入类桁架指数，以期实现STM从框架结构到桁架结构的质变，构建受力合理且几何规则的STM。

1拉压杆模型自动提取方法

显式拓扑优化的共同之处在于结构的边界由拓扑描述函数显式地表达。以MMC拓扑优化方法为例，进行显式拓扑优化的STM自动提取。该方法以MMC优化结构为基础，经过骨架提取、框架提取和形状优化，最终形成受力合理且几何规则的STM。STM自动提取方法流程如图1所示。以下从基本概念、骨架提取、框架提取和形状优化4部分对STM自动提取方法进行阐述。

1.1基本概念

1.1.1 骨架和中轴

骨架（skeleton）定义为图形的极大开球的球心的集合。它在角色动画和网格变形领域广泛使用。中轴（medial axis）定义为图形极大内切球球心的集合，在平面图形中，中轴往往为平面曲线，也称为中轴线。对于平面图形，骨架和中轴并不完全相同，区别甚微。为了方便，统一采用骨架来进行叙述，将骨架和中轴完全等同。

1.1.2 Voronoi图和Delaunay三角剖分

Voronoi图是根据1组共面点对平面的1种剖分。在每一点周围形成1个多边形，多边形内任一点到该点的距离比到组中其他点的距离更近。组中所有点的Voronoi多边形的集合称为Voronoi图。由于Voronoi在平面部分上的等分性特征，可以用来近似平面图形的骨架。Delaunay三角剖分是将平面划分为一系列相连且不重叠的三角形，此三角形是满足空圆性质的一种三角划分。

1.1.3 Crust算法

Crust算法^[21?22]是一种由平面点集构建最可能的多段线算法。对于平面问题，crust算法即为把无序点连成线的过程。如果取样点足够密，那么多段线将越光滑。Crust算法与Voronoi图和Delaunay三角剖分有密切关系。图2为平面图形边界离散点的Voronoi图。根据Voronoi边在平面图形的位置，将Voronoi边分为3类：完全在区域内、部分在区域内和完全在区域外。只保留完全在平面图形区域内的Voronoi边，形成了该平面图形的骨架。若对边界离散点进行Delaunay三角剖分，Delaunay三角形的自由边构成了平面图形的近似多段线边界，如图3所示。

1.2骨架提取

为了从二维优化结构提取一维STM，需要进行骨架提取。根据是否采用模型的内部信息，骨架提取大体上可分为实体方法和几何方法两大类。实体方法又分为细化方法和距离场方法。常见的几何方法包括Voronoi图法^[23?24]、Reeb图法和拉普拉斯方法。对于具有显式边界的MMC方法，几何方法更加适合。拉普拉斯方法多用于由点云表达的空间问题。故对MMC拓扑优化的STM提取采用Voronoi骨架提取法。

MMC方法采用结构拓扑描述函数的零水平集表示结构的边界。这些零水平集的元素形成了优化结构边界的离散点。在优化结构边界与设计域边界相交处添加部分结点，即可形成完整的优化结构边界离散点。绘制该边界离散点的Voronoi图，并通过crust算法形成优化结构的近似边界。采用点的区域内外识别算法，只保留完全在优化结构区域内的Voronoi边，形成带有分支的骨架。最后，通过分支修剪方法^[24?25]，形成多段线骨架。总之，骨架提取实现了从二维优化结构到一维多段线骨架的过渡。

1.3框架提取

多段线骨架由多条平面曲线组成，而STM由多条平面直线组成。从平面曲线到平面直线的过程称之为“框架”提取。框架指提取结果的结构类型往往为框架结构。框架提取可分为候选结点识别、最终结点识别和框架结构构建3个步骤。在多段线骨架中，按端点所处的位置，候选结点可分为端结点、中间结点和分支结点。遍历骨架结点，形成骨架结点的连接关系。只有1个与之相连的结点为端结点，2个与之相连的结点为中间结点，3个及以上与之相连的结点为分支结点。将端结点和分支结点当作候选结点。

若候选结点相距较近，对其进行适当简化。一般来说，如果2个结点的距离小于1个容许值（可取构件较大边长的5%），这2个结点可简化为1个结点，即它们的中点。对于多个相距較近候选结点，从2个最近的结点开始，重复上述的2点简化规则，直到所有点之间的距离不小于这个容许值。为了避免形成较短杆件，对特殊结点，如荷载作用点和支座结点，需进行特殊处理。若候选结点距特殊结点较近时，直接向特殊结点简化即可，相当于删除距特殊结点较近的候选结点。

构建框架结构，需要确定最终结点的连接关系。首先，由于优化结构和骨架具有拓扑一致性，可采用优化结构的洞口信息当作骨架洞口信息。优化结构的洞口采用优化结构的近似边界来识别。优化结构的近似边界通常为多条闭合多段线，每条闭合多段线形成一个多边形，优化结构为最大多边形与其余多边形的布尔差，最大多边形的边界对应于优化结构的外边界，其余多边形的边界对应于优化结构的洞口边界。遍历洞口和最终结点，分别储存洞口周边的结点信息和结点附近的洞口信息。其次，将结点信息和洞口信息相结合，以洞口中心为坐标原点，按逆时针将与该洞口相关的结点依次连接。最后，将荷载作用点和支座结点与最近的结点相连接，可得与优化结构相对应的框架结构。

1.4形状优化

自动提取的框架结构的受力合理性和几何规则性均有所欠缺，可由形状优化来加以改善。为了形成轴力为主的STM，采用类桁架指标作为衡量框架结构与桁架结构的相似度。以类桁架指标为约束的形状优化，最早由Xia等^[8?10]提出并成功应用于STM的拓扑优化构建。以框架结构的自由结点为设计变量，以类桁架指标为约束条件，框架结构的应变能达到最小时，框架结构近似为桁架模型。在形状优化中，可施加平行和对称约束，使STM更加简单实用。

1.4.1 类桁架指标

采用框架单元对框架结构进行有限元分析，进而获得各框架单元的内力。为了减小框架单元所受的弯矩和剪力，采用长细比较大的框架单元。框架单元横截面为矩形，其宽度与构件宽度相同，高度取宽度的0.01倍。由于弯矩和剪力的存在，杆件不再是轴向受力杆件。因此，类桁架指标可定义为

1.4.2 优化列式

在类桁架指标的约束下，使框架结构总应变能达到最小的形状优化问题，可表示为

式中：x为形状优化的设计变量，即框架结构可变结点的坐标列向量；C（x）和I（x）分别为形状优化的目标函数和约束函数；K（x）、F和u（x）分别为框架结构的整体刚度矩阵、荷载列阵和位移列阵；x_max和x_min分别为设计变量的上下限；I_t（x）和I_t，min分别为类桁架指标和类桁架指标的最小值，I_t，min可取接近于1的值，如0.995。

2数值实现

框架结构有限元分析中，各单元结点间既可以传递轴力，也可以传递弯矩和剪力。框架单元自由度如图4所示。框架单元由2个结点i和j构成，每个结点各3个自由度，单元的局部和整体坐标自由度分别为u_e=[u_i1，u_i2，u_i3，u_j1，u_j2，u_j3]^T和U_e=[U_i1，U_i2，U_i3，U_j1，U_j2，U_j3]^T。u_e可由U_e和转换矩阵T得出：

u_e=TU_e，（3）

其中，

框架单元在整体坐标系下的单元刚度矩阵为

K_e=T^TK_elT， （5）

其中，

形状优化采用MMA算法作为最优化算法。目标和约束函数的梯度采用中心差分法求解，步长取单元尺寸的0.1倍，直到设计变量的最大波动小于0.001 m。对于平行和对称约束，可以通过减少相应的设计变量来实现。

3数值算例

对混凝土结构中单侧牛腿和开洞深梁，采用Voronoi提取法自动构建框架结构，并对框架结构进行形状优化，获得类桁架结构的STM。拓扑优化采用MMC拓扑优化代码^[26]。为了便于理解，在STM提取中，采用统一的表示方法：候选结点采用蓝色方形点表示，最终结点采用绿色圆形点表示，形状优化后的结点用蓝色圆形点表示，拉或压杆采用红色实线表示。

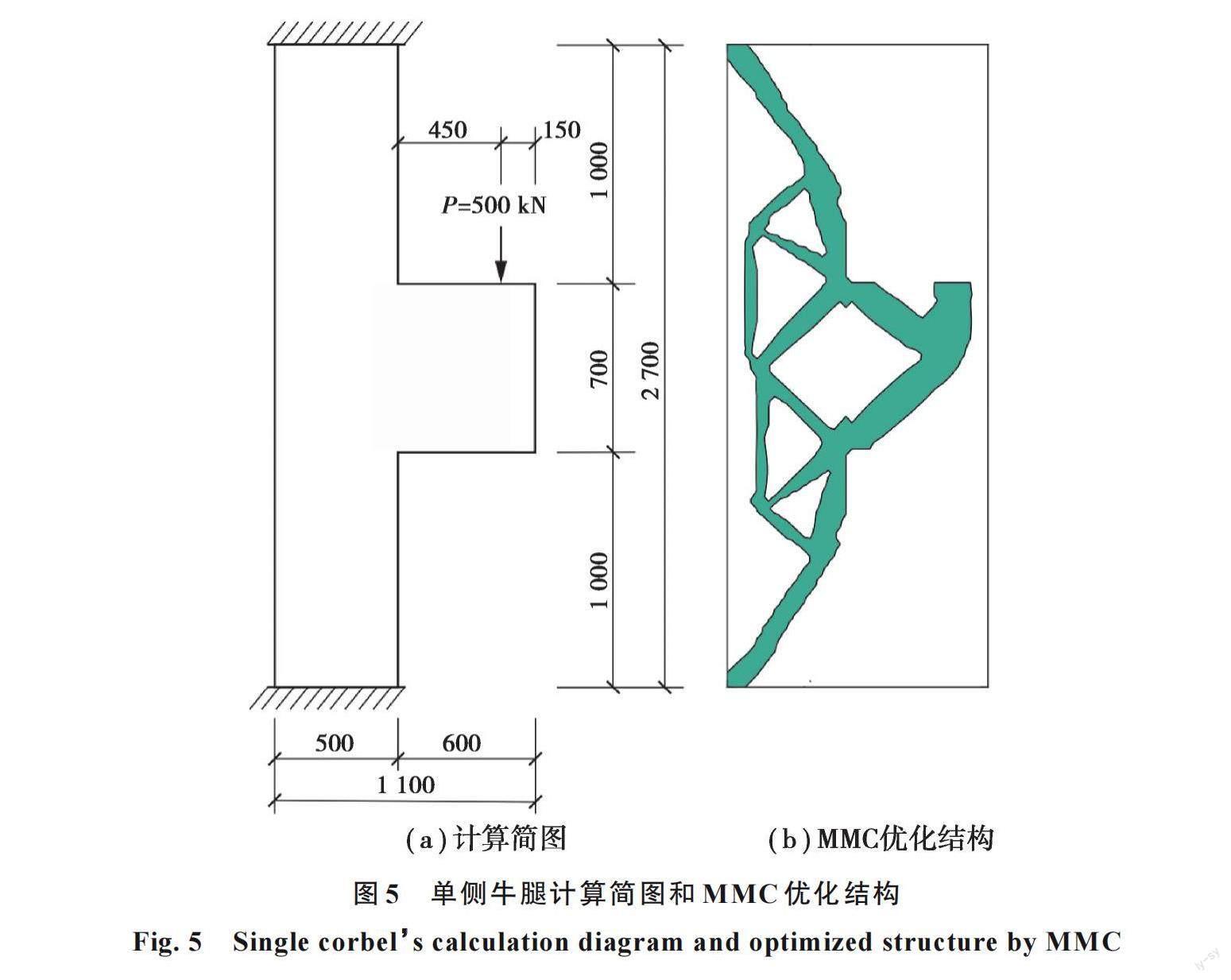
3.1单侧牛腿

单侧牛腿的计算简图和MMC优化结构如图5所示。MMC拓扑优化的参数和过程见文献[19]。

MMC优化结构的边界由677个已知坐标的二维点进行离散，采用crust算法计算该优化结构的近似边界。该边界由6条闭合多段线构成，6条闭合多段线又构成6个多边形。MMC优化结构由最大的多边形与其余5个多边形的布尔差运算生成，MMC优化结构的5个洞口则对应5个较小的多边形（见图6（b）中5种不同颜色的区域）。

复杂的拓扑需要较多的边界离散点，较多的边界离散点生成了较复杂的Voronoi图。经过内外识别，可以生成带有少量细小分支的骨架。经修剪后，可以获得由多段线构成的理想骨架。该骨架较好地满足了拓扑一致性、细性、光滑性和中轴性。

在候选结点识别中，可识别出3个端结点和11个中间结点。若2个候选结点的距离小于135 mm，进行结点简化。若候选结点距支座和荷载结点较近，为了避免较小杆件，只保留支座和荷载结点。

由拓扑一致性可知，骨架和优化结构的拓扑等价。因此，骨架和优化结构具有相同的洞口信息。单侧牛腿结点和洞口信息如表1所示。以洞口中心为原点，从正北方向开始逆时针依次连接各结点，形成最终的STM，如图7所示。

在形状优化中，以类桁架指标为约束条件，框架结构中共11个结点，其中8个结点为自由结点。若只考虑变量的上下限约束，该形状优化共16个设计变量，优化后结构的类桁架指标由0.96增加到1.00。优化后，最为明显的变化是与荷载作用点相连的杆件由倾斜变为竖直，这就保证了该杆件为轴向受压杆件，实现了由框架结构向桁架结构的转变。若考虑部分杆件的平行约束，设计变量数由16减少为14；若再增加沿水平方向的对称性约束，设计变量数由16减少为10。单侧牛腿形状优化如图8所示。单侧牛腿形状优化前后结点平面坐标如表2所示。

3.2开洞深梁

开洞深梁是一类重要的混凝土构件，洞口使得深梁应力分布趋于复杂。开洞深梁的计算简图和MMC优化结构如图9所示。MMC拓扑优化中，混凝土弹性模量为2 0820 MPa，泊松比为0.15，构件的厚度为400 mm，容许体积比为0.35。采用四结点的等参平面应力单元对设计域进行有限元离散，有限元单元的边长为50 mm，有限单元总数为13 200。开洞深梁初始拓扑由36个组件构成。经过309次迭代，达到最优拓扑，最小柔度目标值为17.11 kJ。

开洞深梁MMC优化结构的边界由1 280個点进行离散。通过crust算法形成优化结构的近似边界（见图10（b））。通过近似边界分析，可识别出该优化结构有3个洞口。开洞深梁边界离散点的Voronoi图，如图11所示。开洞深梁骨架和框架提取分别如图12和图13所示。

在开洞深梁的STM中，左侧的倾斜杆件部分跨越了洞口，如图14（a）所示，这一点可以在形状优化中通过约束加以解决。形状优化后STM，如图14（b）所示。开洞深梁形状优化前后结点平面坐标，如表3所示。

4结  论

针对MMC拓扑优化的STM构建，利用Voronoi骨架提取和形状优化，建立了显式拓扑优化的STM自动提取方法，并通过单侧牛腿和开洞深梁验证了其有效性，得到如下结论：

1） STM自动提取方法构建了受力合理且几何规则的STM。

2） Voronoi骨架提取法从MMC优化结构提取了光滑的中轴骨架。

3）以类桁架指数为约束的形状优化实现了STM从框架结构到桁架结构的质变。

参考文献

［1］  Guo X， Zhang W S， Zhong W L. Doing topology optimization explicitly and geometrically—a new moving morphable components based framework[J]. Journal of Applied Mechanics， 2014， 81（8）： 081009.

［2］  Zhang W S， Yang W Y， Zhou J H， et al. Structural topology optimization through explicit boundary evolution[J]. Journal of Applied Mechanics， 2017， 84（1）： 011011.

［3］  Zhang W S， Li D D， Kang P， et al. Explicit topology optimization using IGA-based moving morphable void （MMV） approach[J]. Computer Methods in Applied Mechanics and Engineering， 2020， 360： 112685.

［4］  Yang H， Huang J Y. An explicit structural topology optimization method based on the descriptions of areas[J]. Structural and Multidisciplinary Optimization， 2020， 61（3）： 1123-1156.

［5］  Zhu B L， Wang R X， Wang N F， et al. Explicit structural topology optimization using moving wide Bezier components with constrained ends[J]. Structural and Multidisciplinary Optimization， 2021， 64（1）： 53-70.

［6］  Bruggi M. Generating strut-and-tie patterns for reinforced concrete structures using topology optimization[J]. Computers & Structures， 2009， 87（23/24）： 1483-1495.

［7］  Du Z L， Zhang W S， Zhang Y P， et al. Structural topology optimization involving bi-modulus materials with asymmetric properties in tension and compression[J]. Computational Mechanics， 2019， 63（2）： 335-363.

［8］  Xia Y， Langelaar M， Hendriks M A N. A critical evaluation of topology optimization results for strut-and-tie modeling of reinforced concrete[J]. Computer-Aided Civil and Infrastructure Engineering， 2020， 35（8）： 850-869.

［9］  Xia Y， Langelaar M， Hendriks M A N. Automated optimization-based generation and quantitative evaluation of Strut-and-Tie models[J]. Computers & Structures， 2020， 238： 106297.

［10］  Xia Y， Langelaar M， Hendriks M A N. Optimization-based three-dimensional strut-and-tie model generation for reinforced concrete[J]. Computer-Aided Civil and Infrastructure Engineering， 2021， 36（5）： 526-543.

［11］  Liang Q Q， Xie Y M， Steven G P. Topology optimization of strut-and-tie models in reinforced concrete structures using an evolutionary procedure[J]. ACI Structural Journal， 2000， 97（2）： 322-331.

［12］  Liang Q Q， Xie Y M， Steven G P. Generating optimal strut-and-tie models in prestressed concrete beams by performance-based optimization[J]. ACI Structural Journal， 2001， 98（2）： 226-232.

［13］  Almeida V S， Simonetti H L， Neto L O. Comparative analysis of strut-and-tie models using Smooth Evolutionary Structural Optimization[J]. Engineering Structures， 2013， 56： 1665-1675.

［14］  劉霞， 易伟建. 钢筋混凝土平面构件的配筋优化[J]. 计算力学学报， 2010， 27（1）： 110-114.

Liu X， Yi W J. Reinforcement layout optimization of RC plane components[J]. Chinese Journal of Computational Mechanics， 2010， 27（1）： 110-114.（in Chinese）

［15］  Victoria M， Querin O M， Martí P. Generation of strut-and-tie models by topology design using different material properties in tension and compression[J]. Structural and Multidisciplinary Optimization， 2011， 44（2）： 247-258.

［16］  Zhang H Z， Liu X， Yi W J. Reinforcement layout optimisation of RC D-regions[J]. Advances in Structural Engineering， 2014， 17（7）： 979-992.

［17］  Zhong J T， Wang L， Deng P， et al. A new evaluation procedure for the strut-and-tie models of the disturbed regions of reinforced concrete structures[J]. Engineering Structures， 2017， 148： 660-672.

［18］  Zhong J T， Wang L， Zhou M， et al. New method for generating strut-and-tie models of three-dimensional concrete anchorage zones and box girders[J]. Journal of Bridge Engineering， 2017， 22（8）： 04017047.

［19］  Qiao W Z， Chen G R. Generation of strut-and-tie models in concrete structures by topology optimization based on moving morphable components[J]. Engineering Optimization， 2021， 53（7）： 1251-1272.

［20］  乔文正， 陈国荣， 路国运. 基于可移动变形组件拓扑优化方法的梁柱节点拉压杆模型研究[J]. 太原理工大学学报， 2021， 52（3）： 444-449.

Qiao W Z， Chen G R， Lu G Y. Research on strut-and-tie models of beam-column connections by topology optimization based on moving morphable components[J]. Journal of Taiyuan University of Technology， 2021， 52（3）： 444-449.（in Chinese）

［21］  Amenta N， Bern M， Eppstein D. The crust and the beta-skeleton： combinatorial curve reconstruction[J]. Graphical Models and Image Processing， 1998， 60（2）： 125-135.

［22］  Amenta N， Choi S H， Kolluri R K. The power crust， unions of balls， and the medial axis transform[J]. Computational Geometry-Theory and Applications， 2001， 19（2/3）： 127-153.

［23］  Ogniewicz R， Ilg M. Voronoi skeletons： theory and applications[C]//1992 IEEE Computer Society Conference on Computer Vision and Pattern Recognition， June 15-18， 1992， Illinois， USA. California： IEEE Computer Society Press， 1992： 63-69.

［24］  Karimipour F， Ghandehar M. Voronoi-based medial axis approximation from samples： issues and solutions[C]//Gavrilova M L， Tan C J K， Kalantari B. International Symposium on Voronoi Diagrams， June 27-29， 2012， NJ， USA. Berlin： Springer， 2013.

［25］  Shen W， Bai X， Yang X W， et al. Skeleton pruning as trade-off between skeleton simplicity and reconstruction error[J]. Science China Information Sciences， 2013， 56（4）： 048101.

［26］  Zhang W S， Yuan J， Zhang J， et al. A new topology optimization approach based on Moving Morphable Components （MMC） and the ersatz material model[J]. Structural and Multidisciplinary Optimization， 2016， 53（6）： 1243-1260.

（編辑  陈移峰）