Fe-0.1C-5Mn中锰钢热变形行为研究

岑琼瑛 张本道 严子杰 张 梅

(上海大学 材料科学与工程学院,上海 200444)

近年来,由于全球气候变暖,节能、减排、安全已成为汽车工业实现快速健康发展的迫切需要。汽车轻量化是汽车行业的主要发展趋势。在轻量化、高性能、低成本发展方向的基础上,至今已发展至第三代汽车钢[1-2]。第三代汽车钢以中锰钢、淬火-配分钢(quenching and partitioning,Q &P)为代表,强塑积可达到20～50 GPa·%。中锰钢的锰质量分数为4%～12%,主要通过合金设计和奥氏体逆相变退火(ART annealing)获得超细晶粒的铁素体和亚稳奥氏体[3-6]。

在临界退火前,为获得更细小的奥氏体与铁素体的双相组织,通常在奥氏体再结晶区控制轧制,通过高温变形获得细小的奥氏体再结晶晶粒或扁平的再结晶晶粒,为后续相变提供更多的形核位置[7-8]。

本文采用Gleeble-3500热机械模拟机,在不同变形条件下对Fe-0.1C-5Mn中锰钢进行等温压缩试验,研究其热变形行为。通过试验数据的多元线性拟合和非线性拟合等方法,建立并验证了本构方程和流变应力模型,为中锰钢热加工工艺的制定及优化提供指导。

1 试验材料与方法

试验材料采用Fe-0.1C-5Mn高强度中锰钢,其化学成分如表1所示。在钢锭上截取尺寸φ8 mm×12 mm的高温热压缩试样,在Gleeble-3500热模拟机上进行单道次压缩。采用钽片和高温润滑剂减小由于夹具与试样间摩擦而产生的桶形效应。

表1 试验钢的化学成分Table 1 Chemical composition of the experimental steel

热压缩试验工艺示意图如图1所示。将试样以10 ℃/s的速率加热到1 200 ℃保温3 min,以5 ℃/s的速率冷却至变形温度,保温30 s后进行热压缩。变形温度为900、950、1 000、1 050、1 100、1 150 ℃,应变速率为0.001～1 s-1,压缩量为60%。压缩试验结束后立即将试样水淬以保留其高温变形组织,根据试验数据绘制应力-应变曲线。

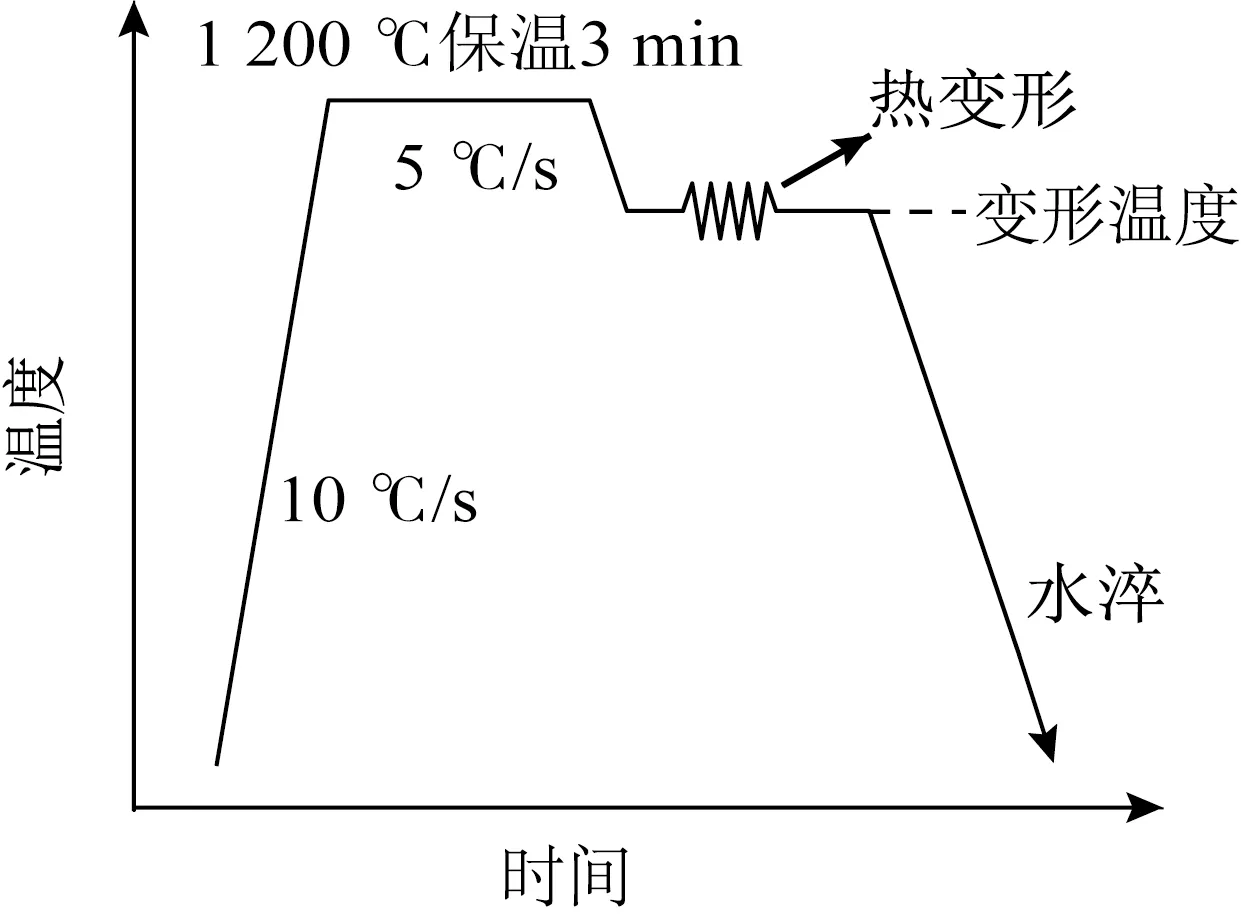
图1 单道次热压缩工艺示意图Fig.1 Schematic diagram of single-pass hot compression process

2 结果与讨论

2.1 应力-应变曲线

金属在热变形过程中随着位错密度的变化会发生不同形式的变形,主要有加工硬化、动态回复(dynamic recovery, DRV)和动态再结晶(dynamic recrystallization, DRX)3种变形机制[9]。

图2为试验钢在不同变形温度和应变速率下的真应力-真应变曲线。可见在不同变形条件下呈现两种不同类型的曲线。在高应变速率下(0.1～1 s-1),曲线以动态回复为主。变形初期,曲线呈弹性变形,随着应变的增加,应力急剧增大,此时主要变形机制为加工硬化。随着应变的增加,发生动态软化,此时动态软化和加工硬化同时存在。当位错密度达到一定值时,加工硬化与动态软化达到平衡,此时应力达到饱和应力σs,并且不再变化。

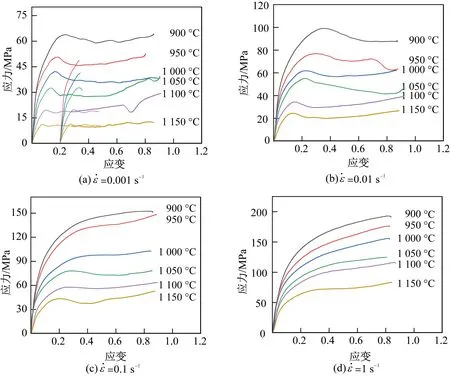
图2 真应力-真应变曲线Fig.2 True stress-true strain curve

在低应变速率下(0.001～0.01 s-1),曲线以动态再结晶为主。随着应变的增加,变形储能达到动态再结晶所需的驱动力,此时的应变值为临界应变εc。随着应变的进一步增加,动态软化和加工硬化作用相同时,曲线达到峰值,对应峰值应力σp。随着应变的持续增加,软化作用占主导地位,应力逐渐减小,至加工硬化、动态回复、动态再结晶三者达到动态平衡,此时曲线达到稳态应力σss,随后应力不再发生变化[10]。

从图2可以看出,随着应变速率的降低和变形温度的升高,峰值应力σp逐渐降低,峰值应变εp逐渐减小。由于高温下驱动力更大,低温时加工硬化率更高,而在低应变速率下,有充分时间吸收能量,当储能超过再结晶势垒时,则发生动态再结晶[11]。因此,变形温度的升高和应变速率的降低有利于动态再结晶提前发生。在低应变速率下呈现明显的动态再结晶的流变应力曲线,在高应变速率下无峰值应力,即明显的动态再结晶行为在高温、低应变速率下出现。

此外,应力-应变曲线存在尾端上翘的情况。这是由于在实际热压缩过程中,试样与模具之间存在摩擦,虽然采用了钽片和润滑剂来减少摩擦,但变形后试样仍存在桶形效应,导致实际检测到的流变应力非真实流变应力曲线,尤其是在高应变下应力偏差较大[12-13]。

2.2 本构方程的推导

流变应力行为可反映热加工过程中的组织变化,流变应力本构方程模型具有重要意义。Zener-Hollomon参数可衡量变形温度与应变速率对热变形行为的影响,其定义为[14]:

(1)

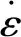
Z=A0[sinh(ασ)]n0

(2)

Z=A1σn1

(3)

Z=A2eβσ

(4)

式中:A0、A1、A2、n0、n1、α、β均为材料常数。其中α约为β/n1的值。上述Z参数的表达式存在一定的约束,式(3)仅适用ασ<0.8时,即蠕变或低应力状态,而式(4)适用于高应力状态,即ασ>1.2时。式(2)适用于广泛的变形条件。

(5)

(6)

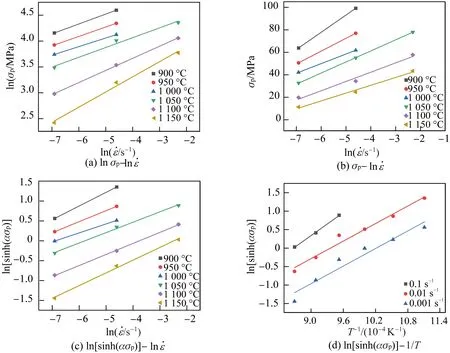
图3 本构方程中线性参数回归曲线Fig.3 Linear parameter regression curves in the constitutive equation

对式(1)、(2)进行整理并取对数,可得:

(7)

对式(7)两边除以n0,得:

(8)

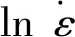
对式(2)两边取对数,得到:

lnZ=lnA0+n0ln[sinh(ασp)]

(9)

将之前求得的Q和α代入式(1)和(2),得到lnZ和ln[sinh(ασp)]的线性关系,如图4所示,求得A0=3.88×1010。

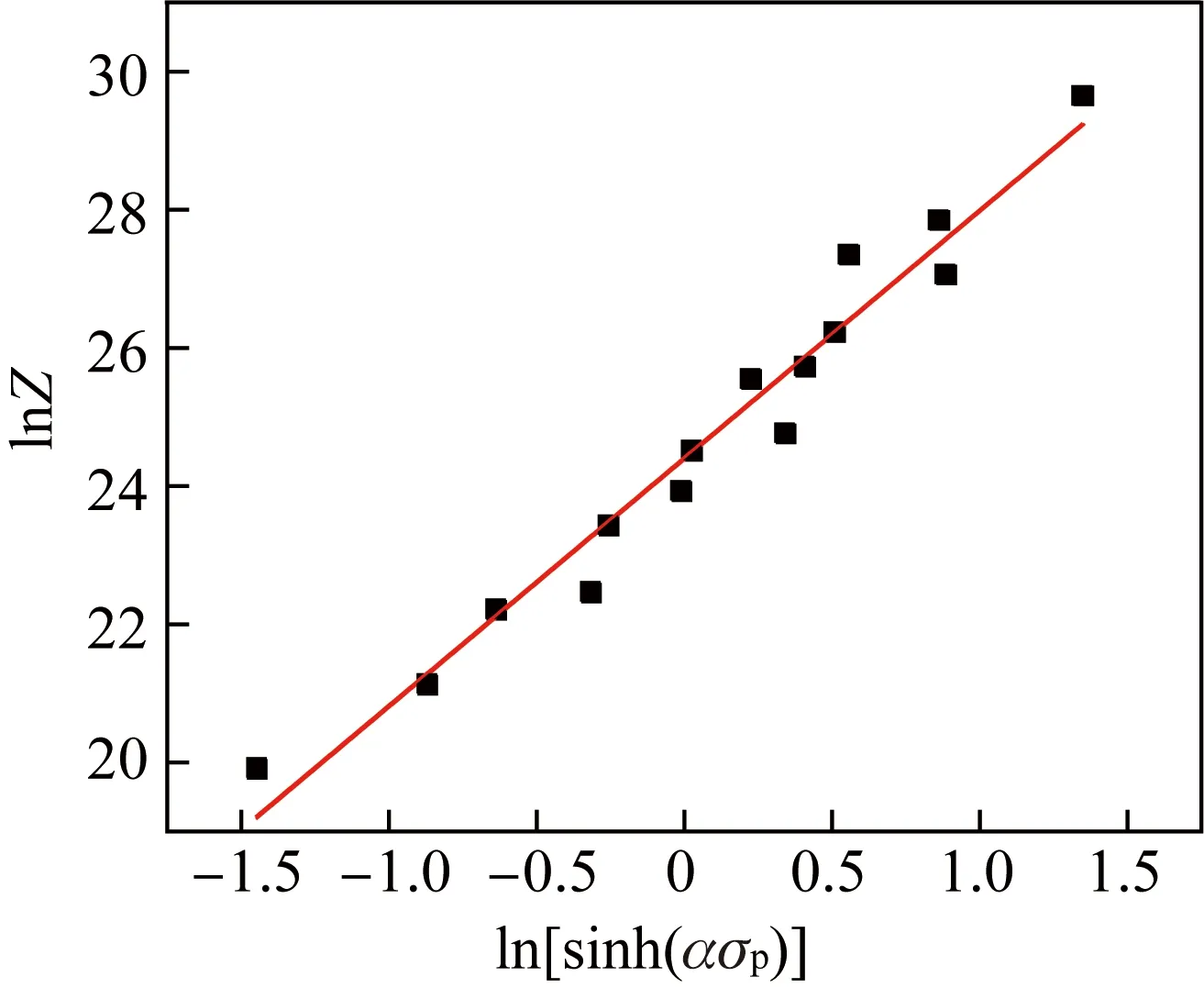
图4 Z参数与峰值应力之间的关系Fig.4 Relationship between Z parameter and peak stress

将A0、α、n0、Q代入本构方程,得到本构方程:

(10)

将式(10)进行整合,得到应力、应变速率与变形温度之间的关系:

(11)

将所求得的各参数代入式(11),则可得到试验钢的峰值应力与应变速率和温度的关系式:

(12)

通过式(11),可计算在不同变形条件下的峰值应力,并与试验值进行对比,以验证所建立的本构方程的准确性[16]。图5为峰值应力试验值与计算值的散点图,并对其进行拟合。计算值与试验值之差的平均值约为13.39 MPa,拟合的R2为0.987 58,拟合曲线接近于y=x。因此,本文所建立的本构方程能够对不同变形条件下的流动应力进行较好的预测。

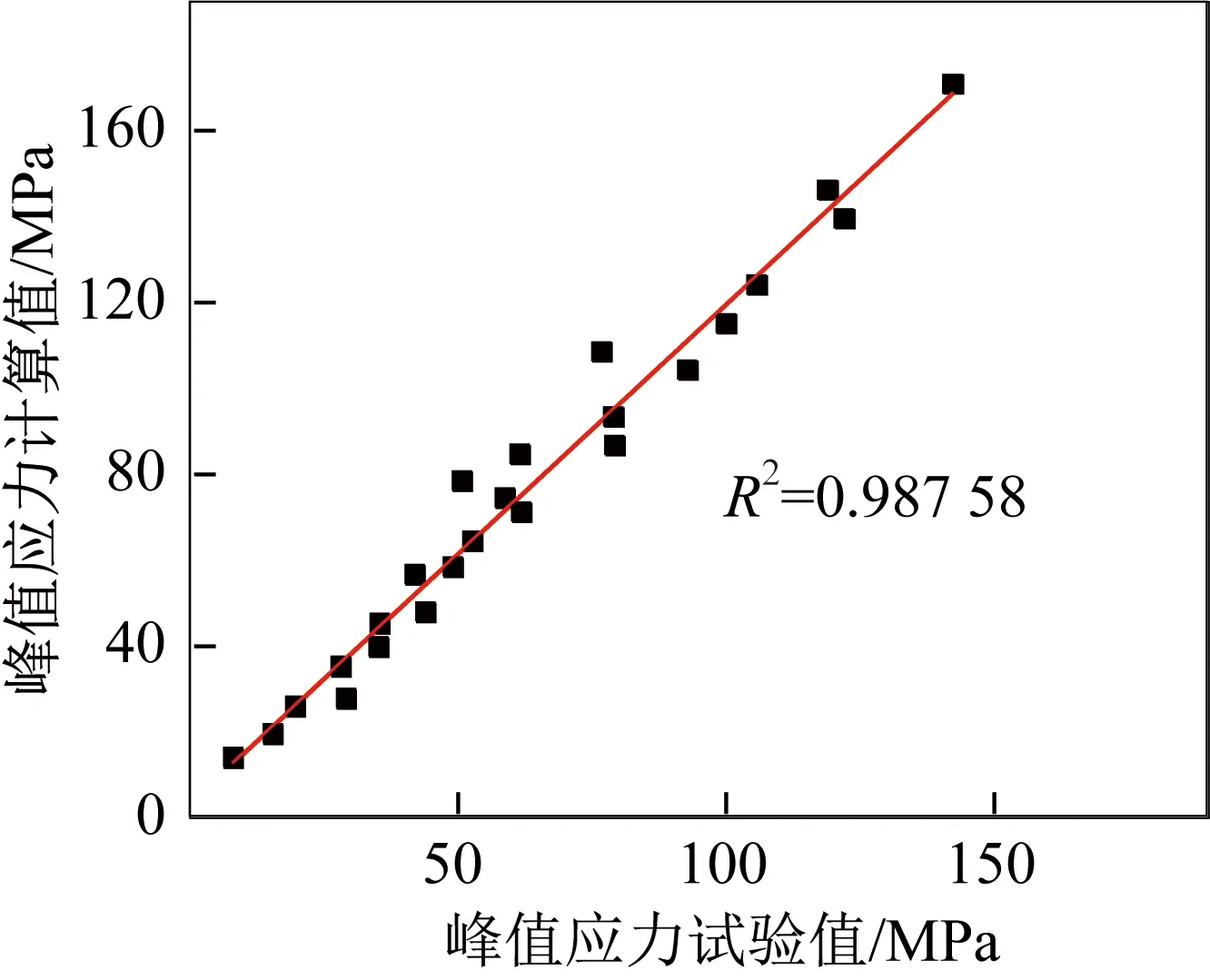
图5 峰值应力试验值与计算值的比较Fig.5 Comparison of experimental values and calculated values of peak stress

此外,Jorge和Balancin提出,力学参数可用Zener-Hollomon参数的简单方程来描述[17]:

Parameter=C·Zk

(13)

峰值应变可以从真应力-真应变曲线中得出,而临界应变则为钢发生动态再结晶时的加工硬化率曲线的拐点,及加工硬化率的二阶导为0时求得[18]。峰值应变、临界应变与Z参数之间的关系可表示为:

ε=C·Zk

(14)

式中:C、k均为材料常数。对式(14)取对数得到:

lnεc=lnC1+k1lnZ

lnεP=lnC2+k2lnZ

(15)

线性回归数据(图6)表明lnεc、lnεP与lnZ呈线性关系,回归得到以下方程:

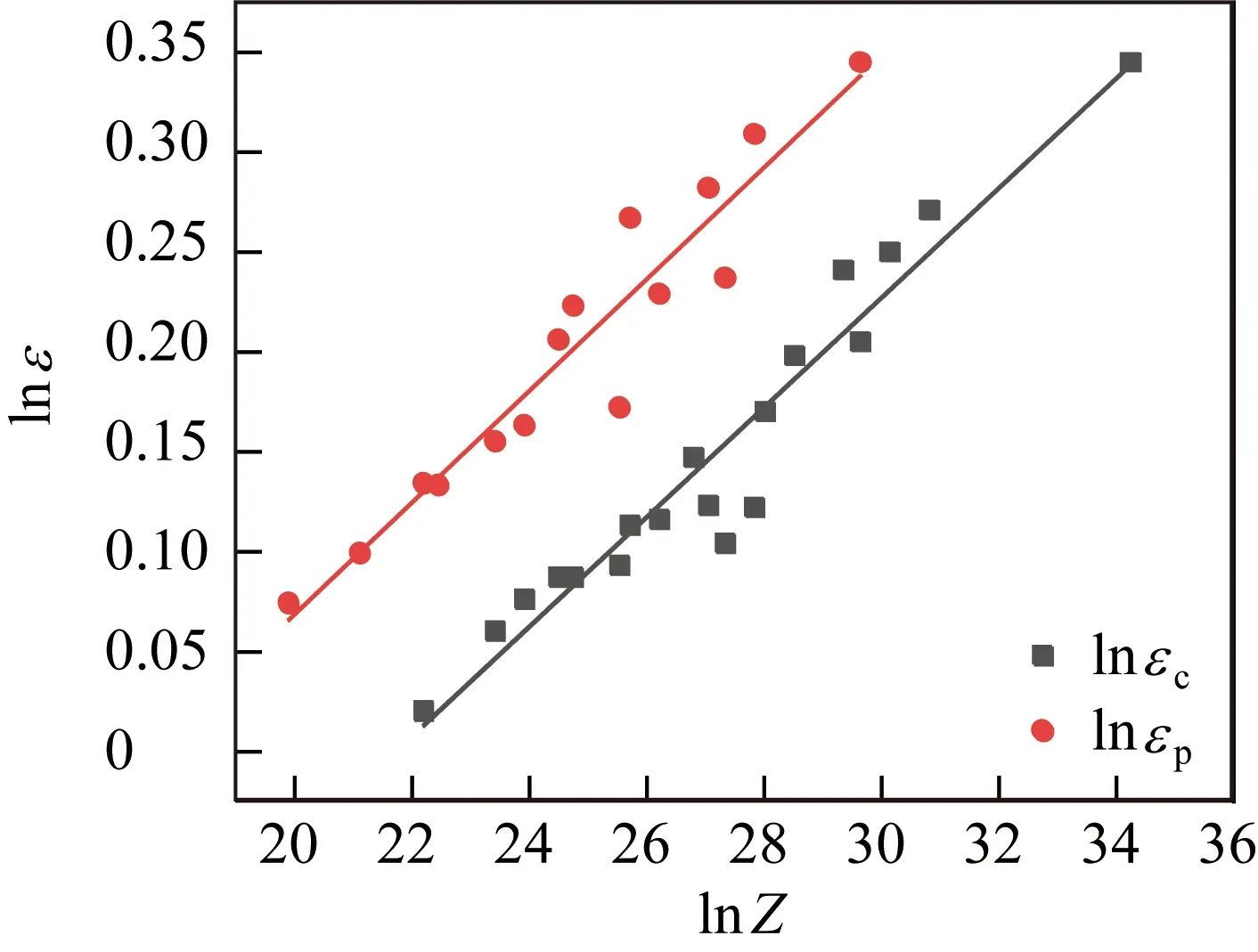
图6 Z参数与峰值应变、临界应变之间的关系Fig.6 Relationship among Z parameter, peak strain and critical strain

εc=0.550 598·Z0.027 45

(16)

εP=0.611 99·Z0.027 96

可以看到lnεc与lnεP之间存在平行关系,斜率接近,因此εc与εP亦存在一定的比例关系,即εc=a1εP,a1为比例常数,a1=0.429。

2.3 动态回复流变应力模型

热加工过程中,流变应力是由加工硬化与动态软化共同作用决定的,并且整个热变形过程中都存在位错密度的变化。在热变形过程中,当应变量小于临界应变时,无动态再结晶发生,此时位错密度(ρ)的演化可能是加工硬化和动态回复的耦合作用。位错密度与应变的关系可通过EM (Estrin and Mecking)模型来描述[19]:

(17)

式中:ρ为位错密度;U为加工硬化速率或系数;Ω为固定变形条件下的动态回复速率;Ωρ是由于位错湮灭和重排而导致的动态回复所引起的。对式(17)进行积分得:

(18)

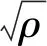
(19)

式中:a为材料常数,根据给定材料恒定,且为单位数量级;b为柏氏失量;μ为剪切模量。

当流变应力达到饱和时,加工硬化和动态软化达到平衡,此时的位错密度也达到动态平衡,即dρ/dε=0,通过式(17)可知,对应的位错密度ρs=U/Ω。通过式(19)得到各状态下的位错密度并代入式(18),通过整理可得:

(20)

在动态回复阶段,对小于临界应变部分的数据进行非线性拟合,得到σs、σ0。将式(1)和(2)进行整合,可得:

(21)

将得到的不同变形条件下的σs、σ0进行线性回归,确定式(21)中的参数,得到σs、σ0的模型:

(22)

(23)

动态回复软化系数Ω可通过非线性拟合得到,其表达式[10]:

(24)

式中:Ω0、mΩ是材料常数;QΩ是动态回复激活能。对式(24)进行多元线性回归分析,可得Ω0=11.8,mΩ=0.072,QΩ=1.34×105。

2.4 动态再结晶流变应力模型

当应变量大于临界应变时,发生动态再结晶,随着应变量的增加,应力逐渐趋于平稳,到完全再结晶时达到稳态应力σss。在动态再结晶区域,位错密度的演化取决于动态再结晶动力学,Avrami方程已被证明能充分表征动态再结晶行为的动力学,如下[20]:

(25)

式中:K和N为材料常数;ε0.5是动态再结晶体积分数为50%时的应变量。动态再结晶的体积分数又可定义为[21]:

(26)

通过式(26),可计算得到XDRX,并得到各变形条件下的ε0.5。对式(25)两边取对数,并进行线性回归分析,可求得N为1.83,K为1.5。

ε0.5与Z参数的关系也满足式(14),对lnε0.5-lnZ进行线性回归,可得ε0.5的k、C分别为0.113、1.54×10-2。

动态再结晶过程中的稳态应力同样可采用Z参数和Arrhenius双曲正弦关系方程进行描述[22],因此对于稳态应力,可采用式(21)的模型进行计算,经过多元线性回归,得到:

(27)

动态再结晶阶段,应变量大于临界应变,将式(25)、(26)整合,可以得到σDRX的模型:

σDRX=σDRV-(σs-σvss)·

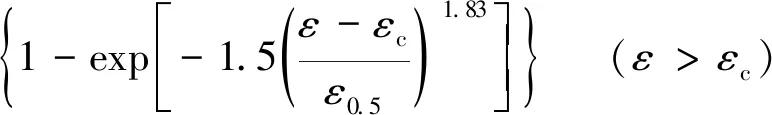
(28)

2.5 流变应力模型的验证

对1 000 ℃变形温度、应变速率为0.001、0.01、0.1、1 s-1,以及应变速率为0.1 s-1、变形温度为900、1 000、1 050 ℃条件下的试验数据进行流变应力模型的验证,包括动态回复及动态再结晶特征曲线,结果如图7所示。可见试验值与模型预测值吻合较好,并且模型预测值在尾端不能较好吻合,这是由于在模型计算中无摩擦对流变应力的影响,呈现了比试验结果更为准确的流变曲线应力特征,修正了摩擦对流变应力的影响。模型计算结果较好地再现了Fe-0.1C-5Mn中锰钢应力-应变曲线演变特征,表明该模型能够准确预测中锰钢高温变形流变应力,可为其实际生产过程中热变形参数的确定提供理论支持。

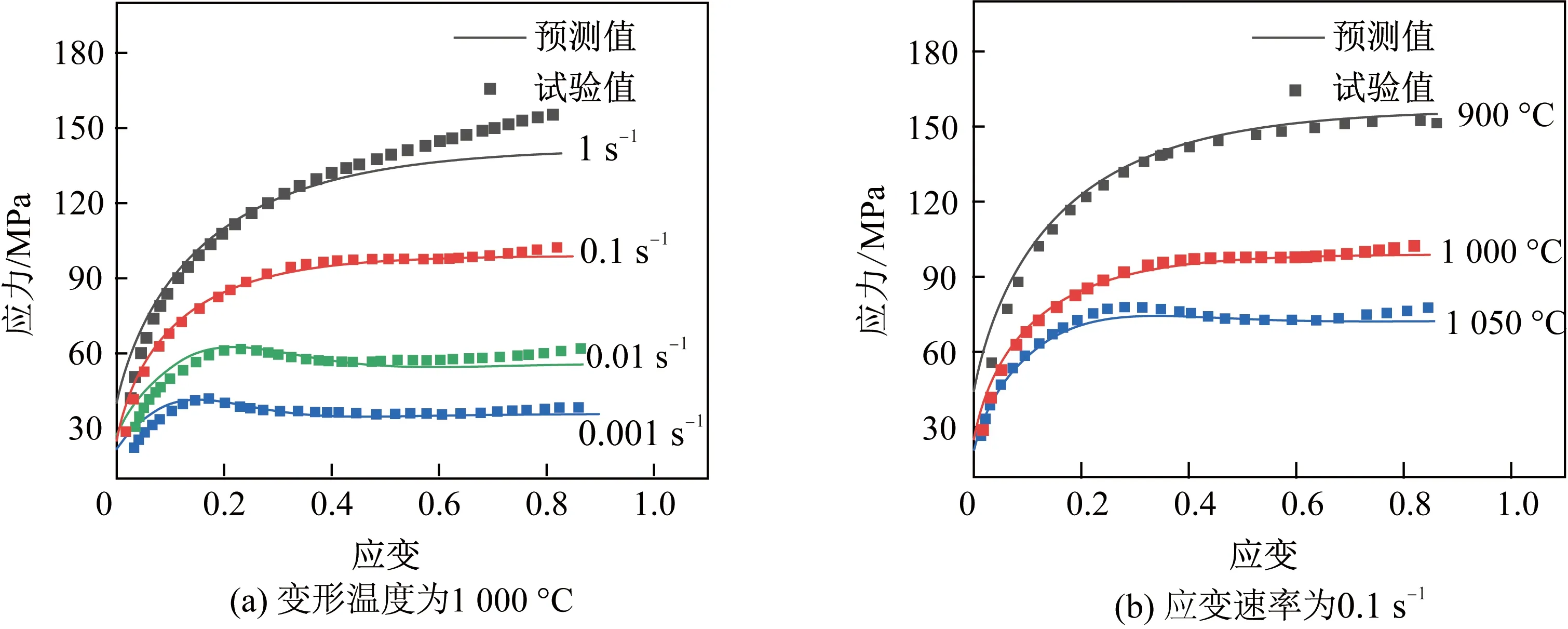
图7 试验钢流变应力试验值与模型预测值的比较Fig.7 Comparison between experimental value and model predicted value of flow stress for the experimental steel

3 结论

(1)Fe-0.1C-5Mn中锰钢存在两种类型的真应力-真应变曲线。在应变速率为0.001～0.01 s-1以及高温、应变速率为0.1 s-1的条件下以动态再结晶为主,在应变速率为1 s-1以及低温、应变速率为0.1 s-1的条件下以动态回复为主。

(2)引入Zener-Hollomon参数,建立中锰钢的本构方程,得到流变应力和动态再结晶体积分数与温度和应变速率之间的关系模型,得到试验钢的热变形激活能为256.317 kJ/mol,且临界应变与峰值应变存在线性关系εc=0.429εP。

(3)为定量描述Fe-0.1C-5Mn中锰钢流变应力与变形条件之间的关系,建立了动态回复和动态再结晶流变应力模型,并证明了模型的可靠性。