基于LMI的时滞系统的分布式H∞负荷频率控制

黄磊

(东北电力大学 电气工程学院,吉林 吉林 132012)

0 引 言

随着电力系统的智能化,当采用开放型的通信网络传输控制信号时,负荷频率控制(load frequency control,LFC)系统会存在较大的时滞和数据丢包等问题［1-4］,导致电网的通信拓扑发生变化,破坏系统稳定性,加大了系统频率控制的难度。文献［5］指出,一个不考虑传输延时的控制器在很小的时滞下,即使性能优越,同样会导致系统动态控制性能的下降甚至不稳定。文献［6］对多区域互联电力系统的仿真结果表明,当传输延时上升至一定数值时,传统的控制方式将无法维持系统的稳定性。因此,为了提升互联系统性能以及控制的稳定性,就必须考虑时滞对整个互联系统的影响。

长期以来,国内外学者已对如何降低传输延时进行了较多研究。文献［7］设计了基于时滞依赖性稳定条件的网络化AGC控制器,获得了保守型比较小的H∞控制器,有效抑制了传输延时对系统稳定性的影响。文献［8］针对包含时滞的PI型LFC控制器,提出基于迭代线性矩阵不等式(linear matrix inequality,LMI)的混合H2/H∞设计方法,将时滞考虑为系统建模不确定性,并通过仿真验证了其有效性。

已有的研究多应用鲁棒方法设计出分散式、集中式控制器来降低时滞对互联电网的影响,未考虑实际运行中因故障或调度变化而造成的网络拓扑变化,忽略了拓扑变化对系统稳定性的影响。因此,本文针对含传输延时的多区域互联系统的LFC,开展分布式鲁棒控制的研究。

1 互联电网LFC系统建模

现代电网是由多个互联的电力系统区域组成的,各个区域通过联络线连接起来,状态方程均可以表示为:

(1)

xi为互联电力系统的状态变量,xi=［ΔfiΔPmiΔPriΔPviΔEiΔPtiei］T。互联电力系统的系数矩阵为:

(2)

(3)

(4)

(5)

式中:Δfi为系统频率偏差;ΔPmi为发电机机械功率偏差;ΔPvi为调速器伺服机位置偏差;ΔEi为频率偏差增量变化;ΔPtiei为区域i的联络线偏差;Di为发电机阻尼系数;Mi为发电机转动惯量;TRi、T1i、T2i为液压调节器时间常数;Ri为调速器调差系数;Kbi为频率偏差因子;Tij为联络线同步系数。

在多区域互联电力系统中,LFC系统中包含互联传输延时的模型如图1所示,此时状态方程为:

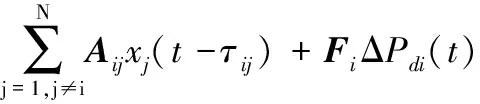
(6)

式中:τij为固定传输延时;ΔPdi为外部干扰。

利用这种具有鲁棒性和传输时滞的分布式结构,使得系统即使在不断变化,也能保证在有限带宽和不可靠的通信网络下正常的运行。

2 分布式H∞控制的LMI设计与稳定性分析

2.1 固定拓扑下H∞控制器的LMI设计

针对无时滞的负荷频率控制系统,基于局部反馈控制的分布式控制器设计为:

(7)

式中:Ki为第i个单元的本地控制器参数矩阵;Kij为第j个单元的解耦协调控制器参数矩阵,如果Kij=0,则控制定律被称为分散式控制定律。

将式(7)代入到多区域互联电力系统的式(1)中,得到如下闭环形式:

(8)

其中假定初始ΔPdi=0。

提出的协议将第i行向量信息的通信矩阵发送到第i个区域系统,第i个区域系统会计算相应的最佳本地和互联增益矩阵Ki和Kij,以减少相应互联项的影响。

考虑互联传输时间延迟,互联的子系统中必须包含延时项,在这种情况下,采用H∞鲁棒控制方法设计了基于LMI的分布式H∞控制方案。带有互联传输延时的分布式H∞控制器设计为:

(9)

式中:τd为固定传输延时。

基于含延时的多区域互联系统的动态(6),在控制器(9)下的第i个控制系统:

(10)

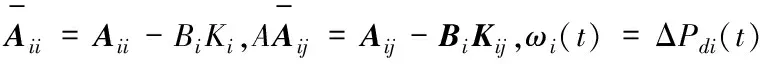
则复合系统为:

(11)

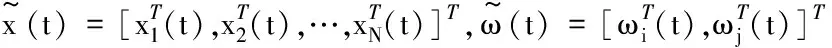
(12)

带有传输延时的H∞设计过程中,对于干扰抑制水平γ,时滞系统需要满足下面要求。

(1) 在没有扰动的时候,即ω(t)=0,假定传输时滞为固定延时,式(11)渐进稳定。

(2) 在存在扰动ω(t),具有零初始条件(x(t)=0,t∈［-τ,0］)的时候,时滞0<τd<τ,扰动输入ω(t)到被控输出x(t)的H∞范数:

(13)

式中:γ为干扰抑制水平,通常取γ>0。

此时系统是内部稳定的,且满足H∞干扰抑制水平γ。然后,利用锥补线性化方法,提出设计LMI条件的非线性极小化问题,求得相应的增益Ki、Kij,从而确保了具有互联传输延时的系统的稳定性。

2.2 切换拓扑下H∞控制器的LMI设计

固定拓扑下并未考虑因通信链路故障或者断路故障而引起的通信拓扑变化,因此应考虑更加实际的场景。这些拓扑变化被建模为一个时变的通信拓扑矩阵。利用该矩阵提出了一种新的闭环电力系统模型。将通信拓扑的变化纳入物理电力系统的动态过程。

由通信拓扑变化引起的结构扰动可以通过以下时变通信矩阵进行建模:

(14)

当Cij=0时,代表通信拓扑的关断,即第i区域与第j区域没有联系;Cij=1时,代表通信拓扑的接通。

此时,包含通信拓扑影响的分布式控制器:

(15)

同时,假设不能添加任意多个链路,即数量收到通信约束引起的上界的限制:

(16)

式中:v为交流网络的总成本约束,v>0;Kij为区域i与区域j之间链路的成本。

假定通信拓扑是时刻变化的,通过通信拓扑检测器可以得知初始通信拓扑,流程如图2所示,则LFC系统算法的计算过程如下:

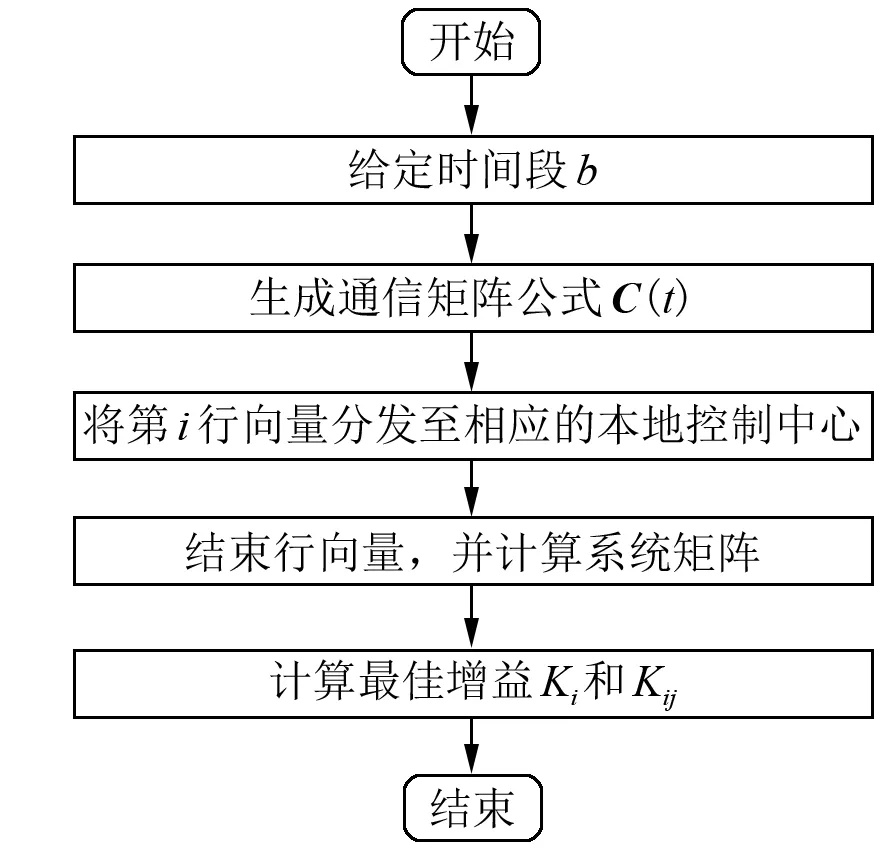
图2 LFC系统控制流程图

(1) 对于每个给定时间段b。

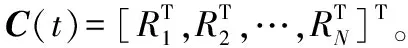
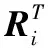
(5) 每个LFC根据最小优化公式计算其本地增益Ki和当cij=1时的最佳互连增益Kij。

(6) 结束。

3 仿真分析

使用由10机39节点测试系统验证所提方法,39节点测试系统分为三部分,每个区域都包括发电机、调速器和涡轮机。39节点新英格兰测试系统参数如表1所示。

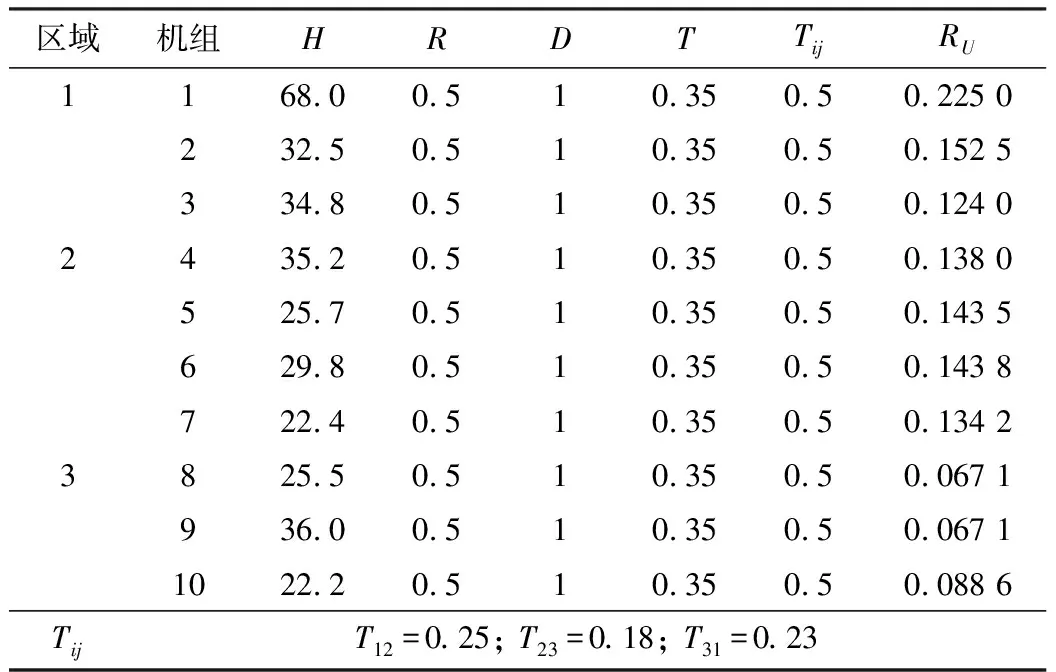
表1 39节点新英格兰测试系统参数

表1中:H为发电机的转动惯量;R为调速器调差系数;D为发动机阻尼系数;T为调节器时间常数;Ru为有功率上升限制;Tij联络线同步系数。

系统通信拓扑如图3所示。

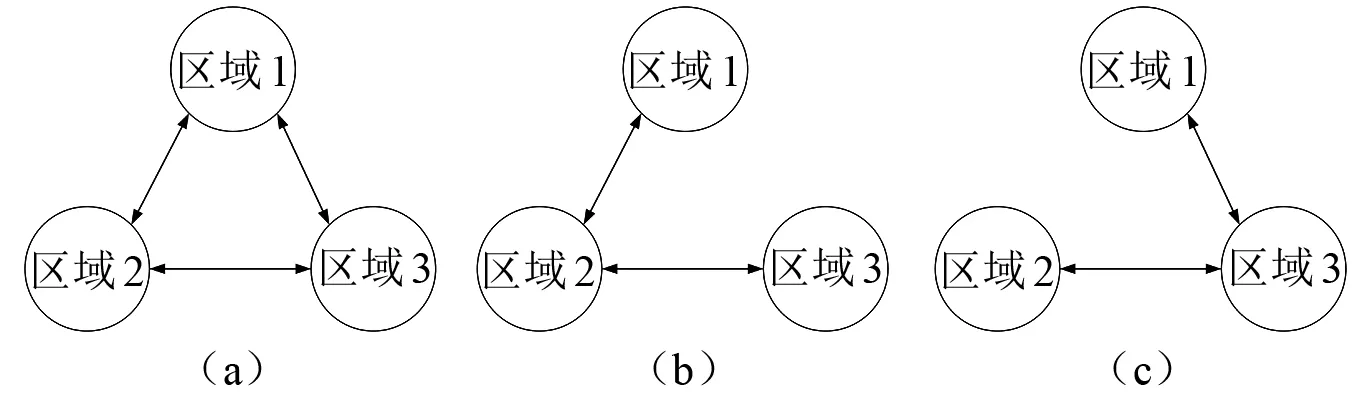
图3 39节点新英格兰测试系统通信拓扑(三个区域)

图3(a)表示所有区域连接正常,图3(b)与图3(c)分别表示区域1与区域2、3之间出现断路故障。选择理想拓扑图3(a),使用所提出的基于LMI的分布式H∞二次控制器和系统原始控制器的仿真结果如图4所示。

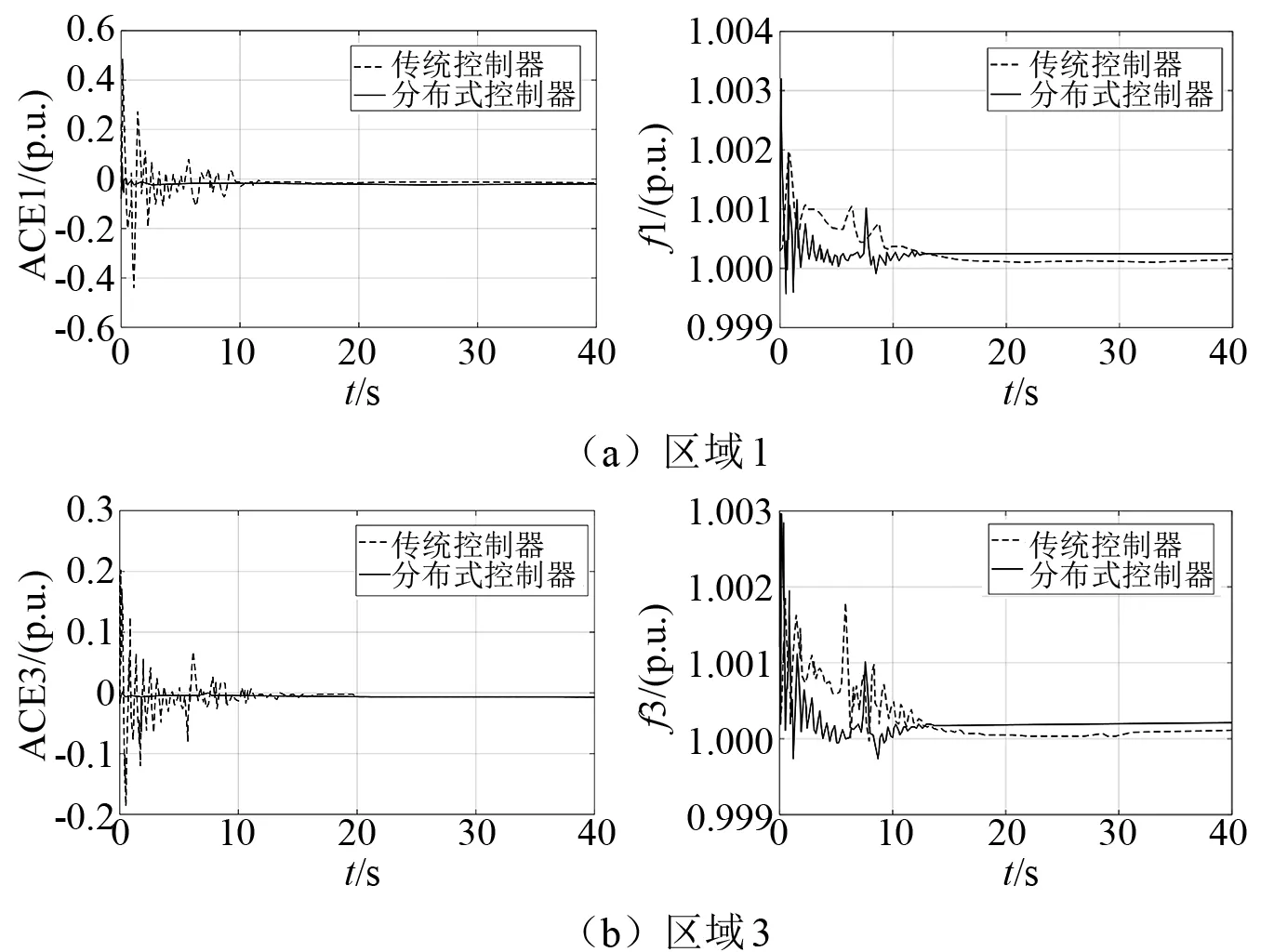
图4 39节点测试系统固定拓扑下基于LMI的分布式H∞控制动态响应

由图4可知,所提出的控制器有效地减少了系统的稳定和过冲时间。从图3(a)到图3(c)的切换拓扑结果如图5所示。

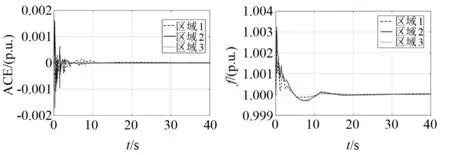
图5 39节点测试系统切换拓扑下基于LMI的分布式H∞控制动态响应

其中切换顺序是任意的,图像表明电力系统在切换拓扑结构下仍可以保持稳定,从而验证了方法的灵活性和鲁棒性。

4 结束语

为了降低传输延时对系统稳定性的影响,本文提出了基于LMI的分布式H∞负荷频率控制策略,同时还考虑到因链路故障或者调峰调频而造成的通信拓扑变化,显著地降低了传输时滞对系统稳定性的负面影响。最后在实际的39节点测试系统进行仿真验证。本文所提出的控制策略较传统控制策略,有效地削弱了传输时延和负荷扰动的影响,综合考虑了因链路故障或调峰调频而造成的网络拓扑变化,较传统控制器可以有效地减少系统的稳定时间和过冲时间。