基于近似梯度下降的稀疏阵列综合方法

王强

（北京跟踪与通信技术研究所，北京 100094）

0 引言

较传统均匀阵列天线，非均匀布阵可在提升阵列天线探测性能的同时，更好地控制天线的资源开销。阵元的非均匀部署破坏了空间采样的周期性质，进而使得空间采样带来的栅瓣效应被极大抑制；此外，稀疏构型不仅减小了系统硬件、计算的开销，还增加了天线的观测孔径，进而改善了天线对角度信息的提取精度［1］。

然而，由于阵列因子（AF）和阵元位置之间不满足线性关系，依托非均匀构型抑制方向图旁瓣相比于传统的激励加窗难度进一步提升。为了解决该问题，大量构型寻优算法被提出，可归纳为三类：第一类方法主要依靠启发式搜索完成构型优化［2］；第二类是基于解析近似的确定类方法［3］；第三类构型综合方法采用压缩感知（CS）同时对阵元的位置和激励幅度进行优化［4］。其目标都是尽可能获取非均匀构型的全局最优解。但由于构型综合问题的特殊性，并无高效算法可以保证获取全局最优构型。

本文聚焦于局部最优构型搜索算法设计，对随机初始构型进行快速寻优。一般来说，梯度下降算法是寻找局部最优解的常用方法。但对于以降低峰值旁瓣电平（PSLL）为目标的阵列综合问题，由于其目标函数的定义形式，无法给出严格的解析梯度。为了使梯度下降成为可能，并尽可能提高算法的迭代效率，本文对目标函数的梯度进行近似以实现高效计算，并由此导出单次迭代内构型的几何变化。在整个优化过程中，方向图的旁瓣按强度被逐个抑制以降低构型整体的PSLL。

1 信号模型

对于一个包含N个阵元的非均匀线阵，其AF定义即：

式中，u=sinθ即方位角正弦。k=2π/λ即系统工作频率对应的波数。xn和An则分别表示第n个阵元对应的坐标和相对激励。为了简化表述，本文采用如下矢量来表征阵列的整体构型：

为了确保系统的工作效率，本文假设构型始终采用最大增益进行辐射。因此，式（1）中的An可以替换为An=ejkxnu0，其中u0即波束指向中心对应的方位角正弦。因此，AF(u)可以被进一步简化为：

由于波束扫描等效于AF在方位正弦域内的平移，对于扫描范围固定的非均匀线阵，其可以等效为一个波束指向固定但旁瓣区域被拉伸的阵列。为了简化符号，本文后续推导不区分u和u'。对于可见旁瓣区域内的PSLL抑制问题，其可以等价为：

式中，S={u|sinθmain≤|u|≤1+sinθmax}表示考虑波束偏转后的可见旁瓣区域。θmain和θmax分别表示波束主瓣边缘和最大扫描角度。dmin代表了综合过程中允许的最小阵元间距，而F(u)为修正后的方向图功率密度，其表达式即：

式中，B(u)为一个中心对称的加权函数，其倒函数即反映了预期的旁瓣局部峰值的起伏形状。不失一般性的，本文取B(u)≡1。

2 基于近似梯度下降的稀疏阵列优化

梯度下降是寻找局部最优最常用的方法。由于式（4）中目标函数包含取最大处理，其精确梯度难以被解析求出。但是，峰值旁瓣所在的方位正弦umax在一个局部区域内近似是固定不变的。因此，预期的梯度可以用F(u)在umax处的梯度近似表征，即：

容易证明，式（6）中的∇RF(umax)可以进一步展开为：

式中，fn=Im[AF(umax)ejkxnumax]。基于该梯度表达式，待求解的构型综合问题可以通过迭代求取AF并生成对应的近似梯度实现。但是，该优化搜索过程并未考虑优化问题中的最小间距约束。因此，除去对峰值旁瓣强度进行梯度下降外，在迭代过程中还需要额外进行构型修正以确保算法输出满足式（4）中的间距约束。下文介绍算法在单次迭代内的具体流程。

2.1 基于NuFFT的快速阵列因子计算

非均匀傅里叶变换（NuFFT）是对时域非均匀采样的数据进行快速频谱分析的加速算法［5-6］。在将待计算方向图的阵列坐标按波长λ进行归一化，并统一按因子2(1+sinθmax)进行放缩后，其AF可以在一定数值精度下通过NuFFT快速求解。由于在优化过程中稀疏阵列的构型会不断变化，本文无法使用针对固定采样方式优化的NuFFT算法。考虑到高斯函数的时频定域性和其计算高效性，可以采用基于高斯插值的NuFFT算法进行快速计算，该算法在各种处理器架构下均有快速实现。

2.2 近似梯度下降

梯度下降过程中一个关键的参数即下降的步长。为了实现快速收敛，该参数通常使用牛顿法或类似方法进行自适应调整。考虑到本文的优化目标并不是在umax处构造一个方向图零陷，该类方法在本文中并不适用。作为替代，本文选择固定单次迭代内的旁瓣功率抑制因子，即：

式中，σdB即设置的对数域下降步长。在整个优化过程中，每一个强旁瓣的幅度按顺序被逐个抑制，进而实现整个可见旁瓣区域内的低PSLL。

为了进一步提升算法的优化效率，对于阵元个数较多的大型稀疏阵列，在单次迭代内可以对多个高旁瓣进行同时下降，即：

式中，umax即第i强旁瓣对应的方位角正弦，其对应的近似梯度和强度抑制因子在式（9）中分别用∇i和σi表示。I表示了单次迭代内同时进行抑制的旁瓣个数，考虑到旁瓣分布的对称性，以上排序以及旁瓣选取过程中仅靠考虑单侧的可见旁瓣区域。需要注意的是，在对I进行设置时，需要避免取值过大，否则容易导致优化在局部最优附近陷入无效震荡。本文使用R'表示单次迭代优化后的稀疏阵列构型矢量，即：

基于式（9）可以对稀疏阵列构型进行迭代优化。当取I=1时，由ΔR导致的AF(umax)的变化量即：

式中，ξ是一个非常小非负量。容易发现，对于对称阵列，其AF的相位在迭代后理论上保持不变。这是由于对称构型对应的梯度同样具备对称性质，因此迭代后构型依然维持对称性。然而，对于非对称阵列，该操作显然会导致抑制旁瓣位置的相位变化。由于不需要给出目标AF的相位，本文所提算法对初始构型的对称性并无要求。需要注意的是，优化过程中对称构型的保持特性仅在理论上成立，在实际优化过程中由于数值误差的累积，构型会逐步退化为非对称构型。如果需要保持构型的对称性，则需要在迭代后消除数值误差，即：

式中，ΔRRev即将ΔR中元素按对称性进行对调得到的对偶修正量。对于按排列顺序编号的阵列，其即ΔR的反向列向量。

2.3 迭代后构型修正

以上旁瓣抑制过程并未考虑阵元间距约束。因此，迭代后构型可能无法满足初始的构型约束，需要进行额外修正。为了减少修正对迭代后方向图的影响，修正处理带来的构型变化量需要尽可能小。不难发现，该构型修正可以表示为如下优化问题：

式中，x‴n=1，…，N即R‴=R″+ΔR'中的对应元素。由于可行域非凸，无法严格求取式（13）对应的最优解，本文选择对其进行梯度下降求解。此时，构型修正对应的目标函数即：

式中，relu(x)=xε(x)。式（14）对应的梯度即：

由于需要对所有组合进行求和，当所有阵元均分布在长度为dmin的线段上时，式（15）对应的最差复杂度为o(n2)。但在实际的综合过程中，由于仅相邻的阵元之间的距离可能小于dmin，因此式（15）实际的计算复杂度为o(n)。考虑到构型修正的效率，以及对输出构型性能的影响，本文统一取波长λ的千分之一作为梯度下降的步长。

2.4 完整迭代过程

由于目标函数自身的非线性特征，仅当取较小的σdB才可以确保在优化搜索过程中实现平滑的PSLL下降，但这同样会极大地恶化算法的优化效率。为了平衡搜索效率以及收敛质量，可以对迭代过程的震荡行为进行检测进而完成对算法收敛性的判断。为了实现这一点，本文将迭代进行分组，并通过分析当前组内迭代贡献的PSLL下降量判断算法是否收敛。结合前面各小节的介绍，整体算法流程如图1所示。

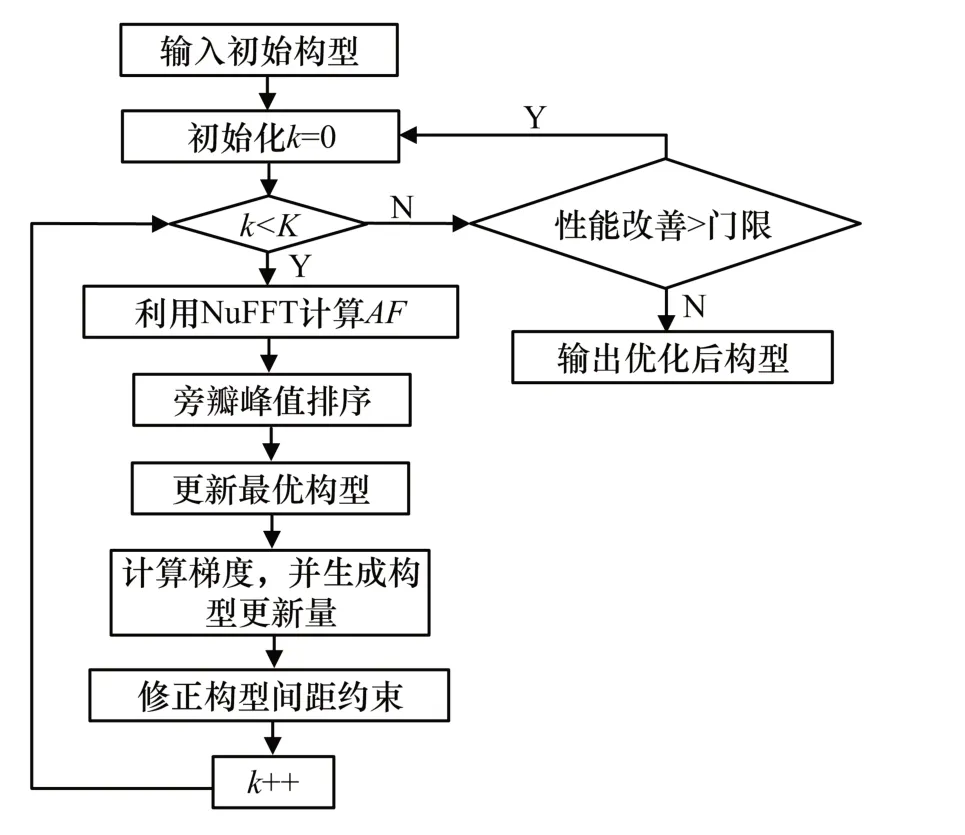
图1 稀疏构型优化流程图

3 数值仿真

由于本文所提算法需要在每次迭代内完成近似梯度计算，而这需要得到当前阵列构型在整个旁瓣区域内的AF。因此，制约算法效率的关键因素在于对稀疏激励进行的频谱分析。得益于一维高斯插值和FFT的高效性，本文可以对所提算法的统计性能进行分析，并和传统的阵列综合算法进行对比。为了确保算法可以收敛，且保持参数一致性，本小节后续仿真案例中均采用固定的分组长度K=2 000，此外迭代的收敛门限取1×10-4dB。

3.1 案例一

本文首先对一个包含N=41阵元的稀疏线阵进行综合，综合过程中要求相邻阵元的最小间距容限为dmin=0.5λ。该阵列的最大扫描角度为60°，故而等效后的可见波瓣区域范围为|u|≤1.866。此外，将待设计的主瓣区域设置为|u|≤0.029 2，当波束指向法向方位时，其对应的方位角范围约为3.3°。

案例一算法输出方向图如图2所示。为了避免优化过程中主瓣过窄导致算法陷入较差的局部最优，算法采用在［-15λ，15λ］区间上随机均匀采样的方式得到初始构型R0，为了提升算法优化效果，并兼顾优化效率，优化过程中采用2组参数：

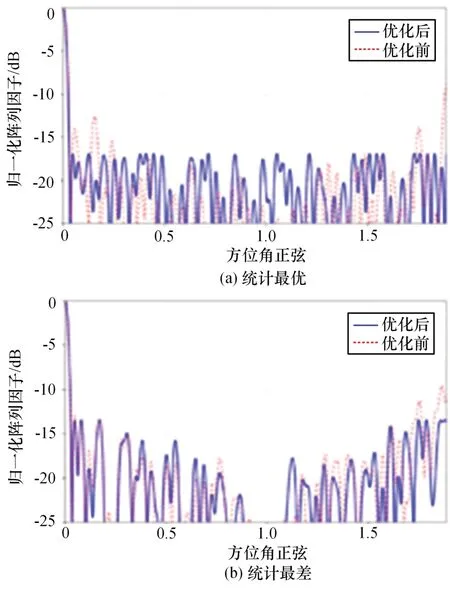
图2 案例一算法输出方向图

1）快速收敛阶段：取同时下降旁瓣数I=2并取抑制步长σdB=-0.1。

2）精密搜索阶段：同时下降旁瓣数不变，仅将抑制步长减小为σdB=-0.01。

将上述优化过程重复500次，图2给出了对应的最优结果以及最差优化结果。在最优结果中，算法有效地将旁瓣能量均匀地分布在整个旁瓣区域内；而最差结果中，则仅在可见旁瓣区域两端获取了等波纹旁瓣，而整体存在较为明显的起伏。该起伏主要是由于构型修正和旁瓣抑制相互矛盾导致的。如果去除最小间距约束，则最差构型可以被进一步优化。为了更加清晰地展现算法的优化性能，本文将间距约束和忽略间距约束情况下的输出PSLL进行了统计，并给出其对应的累积概率密度函数（CDF）曲线，案例一算法输出PSLL统计曲线如图3所示。

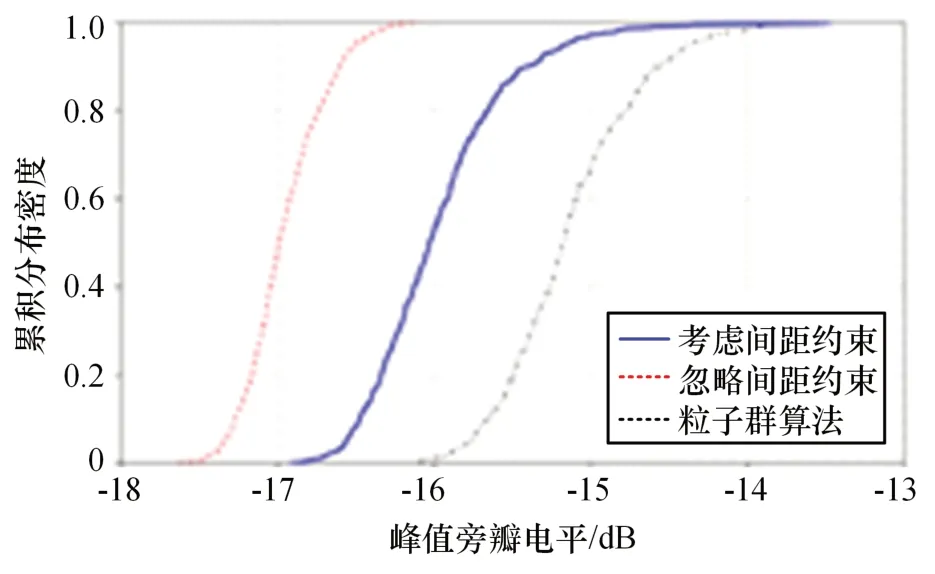
图3 案例一算法输出PSLL统计曲线

由统计结果可以发现，所提算法对随机初始化构型的平均输出PSLL为-15.95 dB。相比之下，忽略间距约束可以将输出PSLL整体降低约1 dB，并且减小输出中高PSLL的托尾范围。这同样从侧面反映了间距约束和旁瓣抑制之间相互矛盾导致算法提前陷入震荡。为了对比所提算法和传统稀疏阵列构型综合算法在优化效率上的区别，本文同样采用粒子群算法对相同的综合需求进行了优化，对应的CDF同样绘制于图3。其中，粒子群算法中共使用了100个搜索粒子，并且总共进行了1 000轮次的迭代搜索。虽然粒子群算法的执行开销显著高于本文所提算法，但本文算法依然有约1 dB的性能优势。这从侧面反映了本文算法通过利用待求解问题的局部解析性质提升了优化搜索的效率，而启发式搜索算法面对该规模的综合任务陷入维度爆炸，难以给出理想的综合输出。

3.2 案例二

为了进一步验证算法对大型稀疏阵列的综合能力，在仿真案例二中，本文将阵元个数增加为N=301，并且将主瓣区域收缩至|u|≤0.003 2，其对应的法向方位波束宽度约为0.37°。此外，其余约束条件和仿真案例一保持一致。类似的，整个优化过程同样分为2个阶段，且参数和案例一保持一致。其中，仅将同时下降旁瓣个数增加为I=10以平衡旁瓣个数增多导致的搜索效率下降。由于分辨率差距较大，在进行初始化时，选择在［-145λ，145λ］范围内对初始构型进行均匀采样。

图4给出了案例二500次仿真中的最优和最差结果。可以发现，2者基本都实现了旁瓣能量在整个区域内的均匀分布，仅局部分布特征存在差异。此外，最差构型中同样并未出现如案例一中的陷入较差局部最优的现象。这可以用大型阵列自由度高、局部最优性质差距不大来解释。

图5给出了所提算法输出PSLL的统计性能。可以发现，算法整体输出的PSLL变化范围较案例一大幅减小，反映了算法对大型阵列进行综合时具有更好的稳定性。

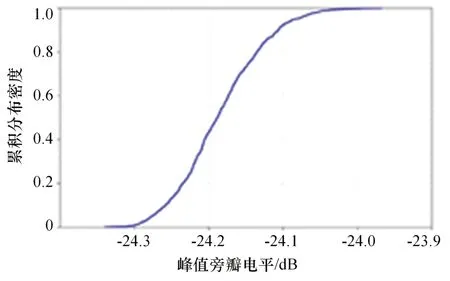
图5 案例二算法输出PSLL统计曲线

4 结束语

本文将采用均匀激励的线性阵列综合问题拆解为逐旁瓣抑制，并利用近似梯度下降完成迭代构型优化调整。通过统计分析，并和其余方法对比，验证了本文算法在效率上的优势，并反映了算法对不同尺度阵列的综合效果。后续研究将着重把算法推广至更为一般的平面阵列，并对迭代调整前的构型初始化方法展开研究。