突风扰动下的扑翼气动功耗和效率变化

谷满仓，张艳来，李晓龙，吴江浩，周 超*

（1. 北京航空航天大学交通科学与工程学院，北京 100191；2. 中国空气动力研究与发展中心，绵阳 621000）

1 引 言

扑翼微型飞行器（Flapping-Wing Micro Air Vehicles， FWMAVs）尺寸小、质量轻、机动灵活，在民用和军用领域都有广泛的应用前景。它们尺寸小、飞行速度低，所以飞行雷诺数比传统飞行器小了几个量级［1-2］。这也导致它们的气动效率低于传统的飞行器。此外，由于扑翼微型飞行器追求小尺寸、低重力，所以很大程度上限制了自身可携带电池的容量。较低的气动效率和较小的电池容量使得扑翼飞行器的飞行时间短，限制了它们在更广阔范围的应用。因此，实现在不同飞行条件中的高气动效率始终是工程师们的研究目标。

在应用中，扑翼微型飞行器可能会遇到各种各样的突风。突风可能由建筑物和树木等障碍物产生，也可能由热对流等条件产生。目前人们对突风如何影响扑翼微型飞行器的气动力进行了大量的研究。Viswanath 等对扑翼施加不同时长、不同相位的正面突风，发现扑翼产生的气动力与扑翼的有效攻角和前缘涡的结构是紧密相关的［3］。Jones 等对扑翼施加不同方向的突风，发现向下突风对扑翼气动力的影响最大；正面突风中，周期平均的气动力与阵风速度基本一致，总体上呈增加趋势，阻力系数也表现出类似的行为；侧向突风中，扑翼的气动力取决于扑翼的速度矢量和阵风速度矢量的相对关系［4］。Fisher 等改变扑翼在湍流中的拍动频率，发现在较高的拍动频率下，流场在每个拍动周期内比较接近，湍流对升力的波动影响对总升力的贡献较小，故认为扑翼固有地可以减弱突风对自身的影响［5］。

总体上看，突风对扑翼微型飞行器气动力的影响已经基本清楚，但是关于突风如何影响扑翼飞行器的气动功耗的研究则比较少。目前仅有少部分突风对鸟类和飞行昆虫的飞行能耗影响的研究。这些研究表明鸟类和昆虫在突风中的能耗增加［6-7］。但是，对活体动物施加突风的能耗结果体现的不仅仅是突风对拍动飞行的气动功耗的影响。活体动物在突风中会调节自身的运动，这些也会影响自身的气动功耗。比如兰花蜂在突风中会伸展后腿以增大自身转动惯量，但是伸展后腿会增大其飞行阻力，增大自身的能耗［8］。因此，直接对活体动物进行实验并不是合适的选择。相反，数值模拟方法可以分离活体实验中生物运动的影响，直接研究突风对拍动飞行的气动功耗的作用。

本文采用数值模拟的方法研究不同方向突风对扑翼飞行器气动功耗和效率影响的问题，分别考虑前向、侧向、竖直三个方向的突风对扑翼这种拍动飞行形式的瞬时和周期平均的气动功耗和效率的影响，并对此进行解释。

2 模型和方法

2.1 扑翼模型

本节介绍论文研究所用的扑翼模型（见图1（a）～（b））、突风模型（见图1b）及扑翼气动力、功耗计算方法。扑翼的模型来自真实的食蚜蝇的翅膀，扑翼翼展R为11.7 mm，平均弦长c为2.8 mm。扑翼在水平面内拍动。本研究中，用拍动角ϕ和俯仰角ψ来描述扑翼的拍动运动，拍动角和俯仰角的定义如图1（a）所示。拍动角是翼根到翼尖的连线在拍动平面内的投影和Y轴的夹角。俯仰角是扑翼和拍动平面的夹角。拍动角ϕ和俯仰角ψ由函数给出

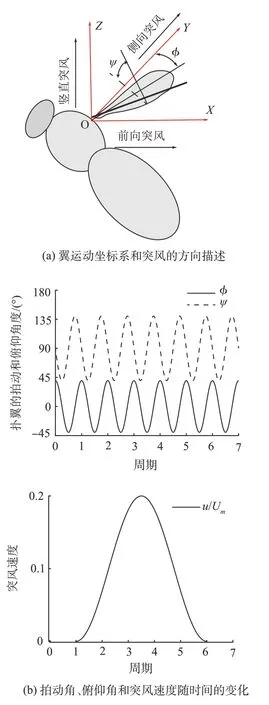
图1 坐标系及运动描述Fig.1 Coordinate system and motion description

式中，Φ为拍动幅度，f为拍动频率，a与攻角相关。参考真实的食蚜蝇的拍动运动［9］，Φ= 80°，f= 200 Hz，a= 50°，扑翼的运动见图1（b）。扑翼二阶矩处的平均拍动速度Um为3.81 m/s。

2.2 突风模型

自然界中突风的速度剖面和“1-cos（·）”型函数很相似，因此，“1-cos（·）”型函数被广泛地用来研究突风对扑翼飞行的影响［3-4］。在本文中，也使用如下的“1-cos（·）”函数来描述突风速度，

式中，b为突风的速度系数，T为拍动周期。在施加突风前，扑翼处于悬停飞行状态。在T= 0 施加突风时，已经对扑翼进行了3 个拍动周期的数值模拟来获得流场稳定的周期数值解。突风在t=T时刻开始增大，方便对比在无突风（0 ＜t＜T）和有突风（T＜t＜ 6T）时的气动功耗。本文通过改变突风速度系数b来改变突风强度。当b= 0.2时，突风的速度剖面如图1（b）所示。本文分别研究前向突风（沿X轴方向）、侧向突风（沿Y轴方向）和竖直突风（沿Z轴方向）对扑翼气动功耗的影响。

2.3 气动功耗评估

本文采用数值模拟的方法来评估扑翼的气动功耗。扑翼拍动时，流动的控制方程是三维不可压缩的N-S方程，

式中，u是流体速度，p是流体压强，ρ是流体密度，v是运动粘度系数。N-S 方程的求解方法和网格验证工作具体与作者在文献中的表述一致［10-11］，这里仅简要介绍。

翼的计算网格是O—H 型的网格，如图2（a）所示。本文分别对计算网格的网格密度、外边界和计算的时间步进行验证。以对网格密度的验证为例，本文设置三种密度的网格：61 × 61 × 61（法向×周向×展向，网格1）、81 × 81 × 81（网格2）和101 × 101 × 101（网格3）。三套网格的第一层网格密度均为0.0001c（c为翅的平均弦长），远场边界30c，每个周期内有400 个时间步。三套网格模拟得到的升力系数CL结果以及力矩系数Mz结果如图2（b）～（c）。可以看出，网格1 与其它两套网格的升力系数有差距，主要体现上下拍动中间升力系数差距较大。网格2 和网格3 的结果十分接近，此时数值模拟结果对网格密度已经收敛。综合考虑数值模拟的准确性和时间成本，在后续的数值模拟中均选择网格密度为81 × 81 × 81（网格2）。类似地，分别对远场边界大小（15c、30c和60c）以及计算用的时间步长（每个周期内200、400 和800 个时间步）进行验证。结果表明，选择30c的远场边界，一个周期内400个时间步时，数值模拟的结果接近收敛，即与网格无关。综上，在后续的数值模拟中，选择网格密度81 × 81 × 81，远场边界30c，一个周期内400 个时间步进行数值模拟。

图2 网格模型及验证Fig.2 Grid and its validation

在通过数值模拟方法得到翼拍动的气动力/力矩后，研究以此为基础评估翼的气动功耗。气动功耗P定义为克服空气阻力所需的气动功耗［12-13］

式中，M为气动力矩，M=［Mx，My，Mz］，Mx，My，Mz分别为绕x，y，z轴的气动力矩；Ω为翼的角速度。定义无量纲的气动功耗CP为CP=CP/0.5ρU3S，其中ρ为密度，U为扑翼的平均拍动速度，S为扑翼的面积。更加详尽的气动功耗求解细节，可以参看文献的介绍［14］。根据扑翼产生的升力及消耗的能量，可进一步计算扑翼气动效率（定义为η=/）。

3 结果与讨论

本部分首先介绍在无突风时扑翼的气动功耗和效率，之后以此为基础，介绍前向突风、侧向突风、竖直突风中扑翼气动功耗和效率的变化。

3.1 无突风的情况

扑翼的运动如式（1）和式（2）所示。无突风时，扑翼的气动功耗如图3（a）所示。在下拍的开始阶段（τ= 0），扑翼的拍动速度比较小，瞬时气动功耗CP接近于0。随着扑翼拍动速度的增大，瞬时气动功耗CP逐渐增大，在大约τ= 0.3时，达到最大值，此时CP= 6。随后，随着扑翼拍动速度的减小，扑翼的气动功耗逐渐减弱到0。因为上拍和下拍的对称性，气动功耗在上拍和下拍过程中是类似的。周期平均的气动功耗为2.95，和真实的食蚜蝇的气动功耗比较接近［9］。

图3 无突风时扑翼的气动功耗和升力Fig.3 Aerodynamic consumption and lift of flapping wing without gust

无突风时，扑翼的升力如图3（b）所示。在下拍的开始阶段（τ= 0），瞬时升力CL接近于0。随着扑翼拍动速度的增大，瞬时升力CL逐渐增大，在大约τ= 3 时，达到最大值，CL没有在拍动速度最大时达到最大值，这主要是由于扑翼前缘涡的形成需要时间，所以瞬时升力达到最大略迟于扑翼的拍动速度达到最大的时间。随着扑翼拍动速度的减小，扑翼的瞬时升力逐渐减弱到0。因为上拍和下拍的对称性，升力在上拍和下拍过程中是类似的。周期平均的升力为1.89。计算得到在无突风时，扑翼产生升力的效率η= 0.64。

基于在无突风时扑翼的气动功耗和产生升力的效率，本文分别分析不同方向突风对扑翼的影响。

3.2 前向突风中升力和气动功耗

前向突风是沿着X轴正方向的突风，此时速度系数b大于0。由于扑翼拍动运动的对称性，在速度系数b＜ 0 时的结果与b＞ 0 的结果是对称的，所以这里重点讨论b＞ 0时气动功耗改变。

不同的前向突风中扑翼瞬时气动功耗如图4（a）所示。无突风时，瞬时气动功耗随时间周期规律性变化。在突风中，瞬时气动功耗产生明显的改变。以第四个拍动周期中瞬时气动功耗的改变为例，瞬时气动功耗在下拍时增加，在上拍时减小（图4（b））。在扑翼拍动过程中，升力垂直于拍动平面，做功较少，所以扑翼的气动功耗主要决定于绕Z轴气动力矩Mz的改变（主要由拍动阻力［12-13］贡献）。不同的前向突风中，Mz的改变如图4（c）。不难看出，在下拍过程中，扑翼的拍动是逆风的，阻力矩Mz的幅度随突风速度的增大而增大，故扑翼的气动功耗增大。而在上拍过程中，阻力矩Mz的幅度随突风速度的增大而减小，故扑翼的气动功耗减小。

图4 前向突风中的气动功耗Fig.4 Aerodynamic consumption of flapping wing with front gust

前向突风中，周期平均的气动功耗如图4（d）所示。在无突风时，周期平均的气动功耗近似保持不变，当存在前向突风时，周期平均的气动功耗先减小后增大。这主要是由于上拍时气动功耗的减小以及下拍时气动功耗的增大不平衡造成的。以第三个拍动周期内的瞬时气动功耗变化为例，瞬时气动功耗在下拍时增大，在上拍时减小，但是下拍时的突风速度小于上拍时的突风速度，因此整体上看周期平均的气动功耗略有减小。

表1 前向突风和相应的定常流对气动功耗的影响Table 1 Effect of front gust strength on aerodynamic power consumption

表2 侧向突风和相应的定常流对气动功耗的影响Table 2 Effect of side gust strength on aerodynamic power consumption

前向突风中，扑翼升力的变化在过往的文献中已有研究［4］，但是并不清楚扑翼产生升力的效率是否变化。在前向突风中，扑翼气动效率如图5所示。相比无突风扰动的情形，在突风作用的前半部分，随着突风速度逐渐增加，扑翼产生升力气动效率下降；之后，随着突风速度减小，扑翼的升力效率增加。无突风时，扑翼气动效率平均值为0.64，而在b为0.2 和0.4 的前向突风中，气动效率的平均值约为0.65 和0.64，气动效率也基本保持不变。

图5 前向突风中扑翼的气动效率Fig.5 Aerodynamic efficiency of flapping wing confronting front gust

综上，前向突风主要改变扑翼瞬时气动功耗（对扑翼驱动电机瞬时功率要求提高），对平均气动功耗和气动效率的影响不大。

3.3 侧向突风中升力和气动功耗

侧向突风是Y轴方向的突风。已有研究表明，从翼尖到翼根的展向流动（b＜ 0）和从翼根到翼尖的展向流动（b＞ 0）对扑翼气动特性的影响是不同的［15-16］。故这里同时设置b＜ 0和b＞ 0的算例研究它们对扑翼气动功耗的影响。在本部分，b的取值分别为-0.4、-0.2、0、0.2和0.4。

不同的侧向突风中瞬时气动功耗如图6（a）所示。存在翼尖到翼根的突风（b＜ 0）时，扑翼气动功耗大致随突风强度增加而减小，反之在翼根到翼尖的突风（b＞ 0）中扑翼的气动功耗变化趋势相反。以瞬时气动功耗改变最显著的第四个拍动周期为例，瞬时气动功耗如图6（b）所示。翼尖到翼根的突风（b＜ 0）一方面引入切向速度，且拍动角平均位置前方的位置切向突风速度向前，而后方位置切向突风速度向后，这使得下拍前半周期拍动和突风引起的切向速度叠加，阻力矩Mz值增加（如图6（c）所示），瞬时气动功耗增加，而下拍后一半周期速度相减，功耗减小；另一方面，翼尖到翼根的突风在展向方向的分量减小了展向流，限制了前缘涡在展向的发展，气动力和力矩减弱（如图6（c）所示），功耗相比无突风状态降低。综合两方面的因素，下拍前半时间扑翼气动功耗升高，从一个拍动周期的结果看，瞬时气动功耗随突风强度增加而减小。当突风方向变化时，我们可以看到在翼根到翼尖的突风（b＞ 0）中，扑翼的瞬时气动功耗恰好有相反的变化。

图6 侧向突风中的气动功耗Fig.6 Aerodynamic consumption of flapping wing with side gust

侧向突风中，周期平均的气动功耗如图6（d）所示。在翼尖到翼根的突风（b＜ 0）中，周期平均的气动功耗减小，而在翼根到翼尖的突风（b＞ 0）中，周期平均气动功耗增大，后者变化更剧烈。整个突风持续时长的气动功耗平均值如表 2 所示。在无突风时，扑翼平均的气动功耗约为2.95。在翼尖到翼根的突风（b＜ 0）中，减小，在翼根到翼尖的突风（b＞ 0）中，增大，改变的最大幅度约为4%。与上一部分类似，本文还计算了扑翼在均匀大小的定常来流作用时的平均气动功耗，定常来流的速度大小等于侧向突风的平均速度，此时平均气动功耗如表 2 所示。对比和，可以看出侧向突风与相应的定常流对平均气动功耗的影响同样差别不大。

在侧向突风中，扑翼的气动效率如图7 所示。在从翼尖到翼根的突风（b＜ 0）中，扑翼的气动效率增大；而在从翼根到翼尖的突风（b＞ 0）中，扑翼的气动效率减小。此外，扑翼面对翼尖到翼根的突风时，气动效率的变化大致与突风强度相关，即增大的气动效率大致关于τ= 3～4 对称分布，而当突风方向相反时，减小的气动效率不再呈现这种相关性，而是在突风强度减小之后增大。在b= -0.4、-0.2、0.2 和0.4 时，平均的气动效率约为0.67、0.66、0.63 和0.62。相对于无突风时的平均气动效率0.64，改变的最大幅度约为4.7%。

图7 侧向突风中扑翼的气动效率Fig.7 Aerodynamic efficiency of flapping wing confronting side gust

综上，翼尖到翼根的突风中扑翼的气动功耗减小，气动效率增大；翼根到翼尖的突风中扑翼的气动功耗增大，气动效率减小。

3.4 竖直突风中升力和气动功耗

竖直突风是Z轴方向的突风。向下的突风（b＜ 0）和向上的突风（b＞ 0）对扑翼气动特性的影响是不同的［17］。故这里同时设置b＜ 0 和b＞ 0的算例研究它们对扑翼气动功耗的影响。在本部分，b的取值分别为-0.4、-0.2、0、0.2和0.4。

不同竖直突风中瞬时气动功耗如图8（a）所示。在向下的突风（b＜ 0）中，扑翼的气动功耗减小，反之向上的突风中扑翼气动功耗增大。以第四个拍动周期中瞬时气动功耗的改变为例，此时瞬时气动功耗的改变如图8（b）所示。在向下的突风（b＜ 0）中，扑翼的瞬时气动功耗在上拍和下拍中都是减小的。这是因为向下的突风中，扑翼的有效攻角减小［17］，使得扑翼产生的气动力减小，所以阻力矩Mz的幅度在上拍和下拍中都减小（图8（c）），因此扑翼的气动功耗减小。反之，在向上的突风（b＞ 0）中，扑翼的有效攻角增大，所以气动功耗增大。竖直突风中，周期平均的气动功耗如图8（d）所示。在无突风时，周期平均的气动功耗近似保持不变。在向下的突风（b＜ 0）中，周期平均的气动功耗减小，减小的幅度随突风速度的增大而增大。在向上的突风（b＞ 0）中，周期平均的气动功耗增大，增大的幅度随突风速度的增大而增大。而且，在相同的突风强度下，向下的突风对气动功耗的影响比向上的突风更加强烈。

图8 竖直突风中的气动功耗Fig.8 Aerodynamic consumption of flapping wing with vertical gust

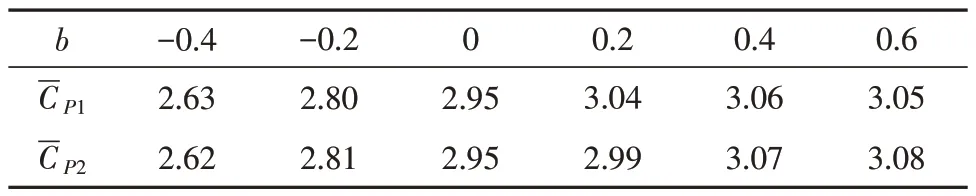
表3 竖直突风和相应的定常流对气动功耗的影响Table 3 Effect of vertical gust strength on aerodynamic power consumption

在竖直突风中，扑翼的气动效率如图9 所示。在无突风时，扑翼的气动效率接近不变。在竖直向下的突风（b＜ 0）中，扑翼的气动效率减小；而在竖直向上的突风（b＞ 0）中，扑翼的气动效率增大。在b= -0.4、-0.2、0.2 和0.4 时，平均的气动效率约为0.61、0.63、0.65 和0.66。相对于无突风时的平均气动效率0.64，改变的最大幅度约为4.7%。

图9 竖直突风中扑翼的气动效率Fig.9 Aerodynamic efficiency of flapping wing confronting vertical gust

综上，在向下的竖直突风中，扑翼的气动功耗减小，气动效率同样减小；在向上的竖直突风中，扑翼的气动功耗增大，气动效率同样增大。向下的突风对扑翼的影响更加明显。

3.5 不同方向突风影响分析

最后，本文综合气动能耗和效率两方面的结果，对比分析不同方向突风的影响。

首先讨论瞬时气动功耗。瞬时气动功耗与电机输出特性密切相关，瞬时气动功耗高对电机最大输出功率有较高的要求，瞬时气动功耗（与拍动运动驱动力矩变化一致）的较大变化会引起机构输出运动的变化，进而改变拍动运动规律。观察图4、图6 及图8 的结果我们可以看出，相同突风强度下，前向突风所引起瞬时气动功耗峰值最大且同一拍动周期内气动功耗的波动也最剧烈，突风影响最强。其次是侧向突风，突风影响最弱的是竖直突风。

其次讨论周期平均的气动功耗。从气动功耗变化上，尽管翼根至翼尖方向侧向突风影响最强，其次是竖直突风和前向突风。但需要指出的是，扑翼飞行器多为双翼布局，侧向突风出现时，左右两翼的突风方向刚好相反，而这在某种程度上会削弱侧向突风对扑翼平均能耗的影响。

最后讨论气动效率。向下的竖直突风对扑翼的气动效率影响最大，其次是翼根到翼尖的突风，前向突风对气动效率的影响不大。

3.6 水平与竖直突风叠加影响初步探究

为进一步分析不同方向突风同时作用对扑翼飞行的效率以及功耗的影响，研究分别计算了“前向突风峰值速度0.2+竖直突风峰值速度0.2”和“前向突风峰值速度-0.2+竖直突风峰值速度-0.2”的算例，并且和相应的突风单独作用时，气动功耗的叠加结果做了比较，如图10所示。

图10 不同方向突风作用时气动功耗的变化Fig.10 Aerodynamic power consumption of flapping wing with gusts from two directions

从图10 可以看出，相比无突风时周期平均的气动功耗几乎不变，水平前向突风与竖直向上突风共同作用时，周期平均的气动功耗先增大后减小，而水平与竖直反方向的突风共同作用时，周期平均的气动功耗表现刚好相反，即随时间先减小后增大。

为了探究突风扰动叠加影响是否是线性的，研究还将竖直突风与水平突风共同作用的结果与多个方向单独突风的叠加结果进行了比较。水平前向突风与竖直向上突风情况的对比结果显示，水平、竖直方向突风单独作用得到的气动功耗叠加值随时间变化与两突风同时作用下的功耗结果变化趋势相同，即突风作用仍能保持，但二者具体数值相差较大。水平后向突风与向下突风的情况与此类似，且数值差别更大。这些结果表明，气动功耗与不同方向突风的关系，不符合线性叠加，即存在多个方向突风相互影响时，突风共同作用下功耗变化非线性较强，后续亦需要仔细设计算例，进行专题研究。

4 结 论

本文采用数值模拟的方法研究了典型的扑翼在前向、侧向和竖直突风中气动功耗和效率的变化情况。主要结论如下：

（1）在前向突风中，扑翼的瞬时气动功耗有较为明显的改变，但是因为上拍和下拍过程中，气动功耗的变化是反向的，所以平均的气动功耗变化不大。前向突风对扑翼的平均气动效率影响也不大。

（2）在侧向突风中，翼尖到翼根的突风使得扑翼的气动功耗减小，气动效率增大；翼根到翼尖的突风使得扑翼的气动功耗增大，气动效率减小。

（3）在竖直突风中，向下的突风使得扑翼的气动功耗减小，气动效率减小；向上的突风使得扑翼的气动功耗增大，气动效率增大。向下的突风对扑翼的影响更加明显。

（4）无论突风的方向如何，突风对平均气动功耗的影响可以用与突风方向相同、大小等于突风平均速度的定常来流模拟，它们对平均气动功耗的影响是相近的。

（5）为了使扑翼飞行效率更高，在飞行中可适当利用向上的突风，应避免向下的突风。相比之下，悬停状态时单纯前向突风和侧向突风对扑翼气动效率（平均升力与平均气动能耗的比值）的影响更弱。