气体扩散层分层设计对PEMFC电堆性能影响研究

王万腾，李 楠，白雪宜，杨 抖，栗 航，李贵敬

（燕山大学车辆与能源学院，秦皇岛 066004）

前言

质子交换膜燃料电池堆作为车用燃料电池发动机的核心部件之一，其性能与燃料电池发动机的效率密切相关，同时，水热管理性能也影响着燃料电池堆的功率密度和耐久性，且严重制约着燃料电池堆作为车用动力的大规模化商用。热管理方面，温度太低可能会导致催化剂和膜质子电导率的降低，太高则会导致膜的降解。水管理方面，膜电极液态水饱和度太高会阻碍反应气体的传输，太低则会降低质子电导率。因此，通过流场结构设计和膜电极材料、结构方面的提升来改良燃料电池堆性能是近几年的研究热点。

燃料电池水热管理的提升对于其性能发挥有着巨大作用。郑文杰等［1］建立了整车燃料电池热管理系统模型，分析了电堆出水温度在不同工况下的影响因素，为整车开发过程燃料电池电堆热管理改善提供了参考。Zhang 等［2］提出了一种全尺寸三维的风冷电堆模型，研究发现增加冷却气流流量可以改善温度和反应物分布的均匀性。Zhang 等［3］讨论了气体扩散层孔隙率从0.2 增大到0.6 时对氧气不均匀性和电流密度的影响。Zhang 等［4］建立了大尺寸的带有金属极板的6 层短电堆模型，研究了电堆内部反应物和温度的均匀性。Chen等［5］建立了预测电堆寿命的退化模型，从热力学和经济学的角度分析了电堆在退化过程中的性能特性。Yu等［6］通过遗传算法优化阴极和阳极在不同方向上的最优三段式分布的气体扩散层孔隙率，以改善燃料电池的输出性能。Prince 等［7］利用Taguchi 方法同时优化了气体扩散层孔隙率和催化层孔隙率来改善膜的水合程度。Zhu 等［8］提出了一种新的评价参数来分析不同运行条件下电堆的性能和均匀性。

综合以上可以发现，目前研究主要集中在改变孔隙率改善单电池性能，以及单独地分析和提升电堆性能。因此，本文将梯度孔隙率设置应用于电堆的研究，提出了一种气体扩散层分层设计的5 层短电堆模型，5 层单电池从上到下在阴极和阳极分别设置了不同梯度孔隙率的气体扩散层：Case1，0.4-0.4-0.4-0.4-0.4；Case2，0.4-0.5-0.6-0.5-0.4；Case3，0.6-0.5-0.4-0.5-0.6。通过三维、非等温的单相的CFD 电堆模型研究了分层设计的气体扩散层对电堆内不同层内的氧气浓度均匀性、水浓度均匀性、温度均匀性、电堆均匀性等的影响，同时还模拟了在电堆缺气情况下气体扩散层梯度孔隙率对电堆性能影响，研究发现，Case2：0.4-0.5-0.6-0.5-0.4 可以最大程度地改善短堆外层单元和内层单元各项参数的均匀性，这有利于延长电堆使用寿命。

1 电堆模型

1.1 电堆几何模型

本文建立了包含5 个单电池的短电堆模型，如图1（a）所示，结构包括了外层的两个端板（用于传导电流和提供结构支撑），以及内层的膜电极组件（MEAs）。膜电极组件又包含了带有冷却流场的极板（BP）、气体扩散层（GDL） 、催化层（CL） 、质子交换膜（PEM）。集流体上的流场简化为Z 型流场。短电堆模型从上到下的单电池单元分别命名为Unit1、Unit2、Unit3、Unit4、Unit5。阴极和阳极的气体进、出口位置和液冷流道进、出口位置如图1（b）所示。电堆模型的几何参数如表1所示。

图1 电堆模型

1.2 电堆数学模型

为了使PEMFC 模型在符合在实际运行条件下尽量简化，本文进行建模的时候考虑了以下假设［9］：

（1） PEMFC 电堆是在稳态的非等温条件下运行的；

（2） 反应物为不可压缩的理想气体，且流动为层流；

（3） 膜电极为各向同性且均匀的多孔介质；

（4） 忽略重力对模型的影响；

（5） PEM不允许通过任何气体。

基于以上假设，本模型的控制方程如下。

连续性方程：

式中：ε表示多孔介质（GDL 或者CL）的孔隙率，ε=1表示的是阴、阳极的气体流道区域；ρ表示反应物密度；u→表示流体的速度矢量；Sm表示质量源相。反应发生在催化层中，因此，在阴、阳极的流道与GDL中，Sm= 0，在阴极和阳极的CL中，Sm的表述如下：

式中：F表示法拉常数；MH2、MH2O和MO2分别表示氢气、水和氧气的摩尔质量；jcath和jan表示阴极和阳极的交换电流密度。

能量守恒方程：

式中：cp表示定压比热容；T表示电池温度；keff表示有效导热系数；SQ表示能量源相，其表达式见式（5）。

式中：I表示表面电流密度；Rohm表示欧姆阻抗；β为化学能转化为热能的效率；hreact表示反应焓；ηcath，an表示阴极和阳极过电位。

动量守恒方程：

式中：p表示气体压力；μ表示动力黏度系数；Su为动量源相。其中阴、阳极流道的动量源相为0，多孔介质区域的动量源相表述如下：

式中K表示渗透率。

物质守恒方程：

式中：Ck表示物质k的浓度；Deffk表示物质k的有效扩散系数；Sk表示物质k的浓度源项。反应发生在催化层中，因此，阴、阳极流道和GDL 中的Sk= 0，催化层中的Sk表达式如下：

物质有效扩散系数：

式中：Drefk表示参考扩散系数；Tref表示参考温度；pref表示参考压力。

电子和质子输运方程：

式中：σsol和σmem表示固相和膜相电导率；φsol和φmem表示固相和膜相电势；S表示电流源相，其表达式见式（15）和式（16）。

质子交换膜电导率［10］的描述如下：

式中λ为膜的含水量。可见σmem的值与膜的温度和含水量有关。

求解催化层内电化学反应的Butler-Volmer方程：

式中：jref，an和jref，cath为单位活性面积的阳极和阴极的参考交换电流密度；A为比活性表面积；γ为浓度依赖性指数；α为传递系数；R是气体扩散常数；η为局部表面过电压，其表述见式（20）和式（21）。

式中Uoc为阴极开路电压。

边界条件和模型设置如下。

流场内反应气体的流动被认为是充分发展的流动，阴、阳极进气歧管进口速度u分别为如下公式［3］：

式中：N为单电池数量；ξ为化学计量数；Iref为参考工作电流密度；ω为反应物的质量分数；Ach为流道横截面积。

电堆出气歧管出口条件设为大气压，模型中所有壁面均设置为无滑移条件。阳极端板接地，电势为0，阴极端板电势设置为运行电压，极板表面温度为293.15 K。另外，液冷流道中液体的流速为0.1 m/s，冷却流道液体进口温度为293.15 K。另外还将两侧端板的壁面设置为自然对流传热的边界条件，即环境温度为293.15 K，传热系数为20 W/（m2·K）。边界条件和模型参数详见表2。

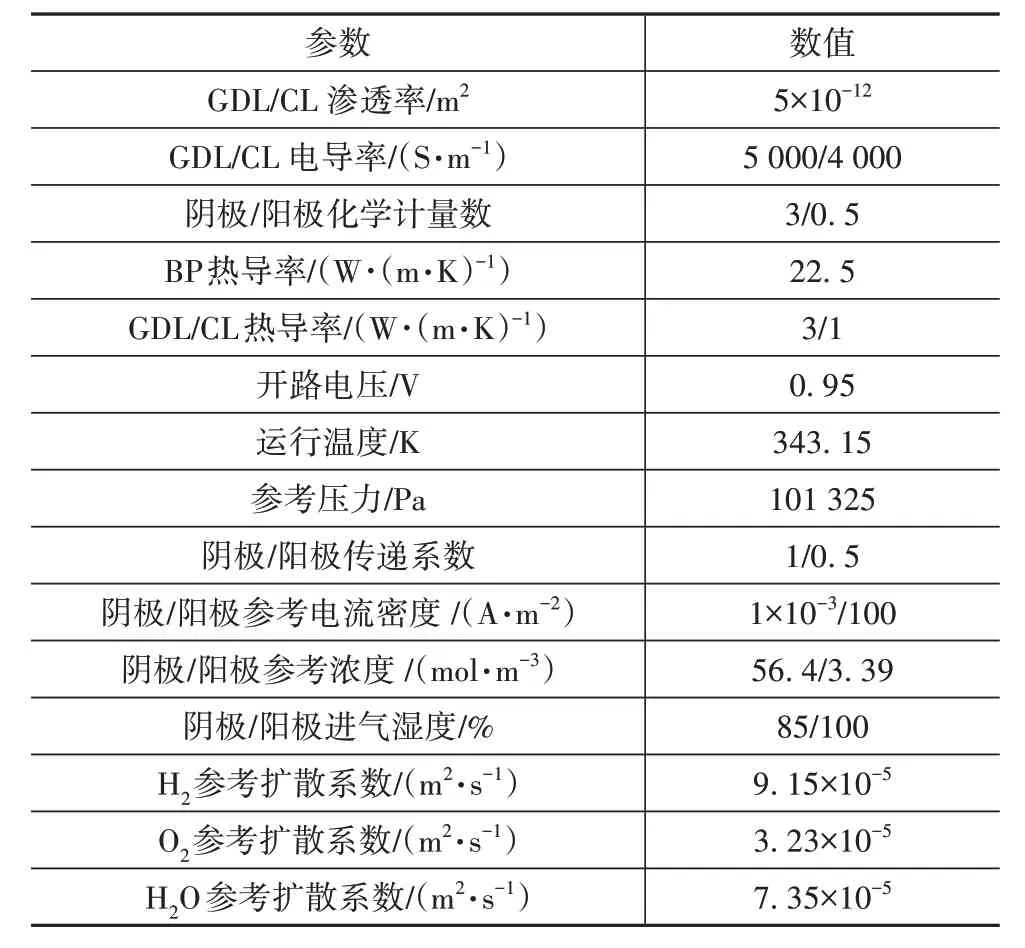
表2 边界条件和模型参数

2 模型验证

网格独立性测试对于模拟结果的准确性至关重要，因此本文分别计算了596 371、756 687、824 542、917 002、1 101 922 5 组不同数量的网格，从而验证后续的所有模拟结果不受网格数量的影响。表3 显示了5组不同网格数量下在电压为0.55 V 下的电流密度和与上一组网格的相对误差，可以看出随着网格数量的增加，计算所得的电流密度逐渐减小并趋于稳定，网格数量917 002 和1 101 922 相比上一组网格的相对误差均低于0.5%，因此可以保证本文模拟结果不受网格数量影响，后续模拟为了节省计算时间，采用网格数量917 002进行计算。

另外，为了充分验证本文建立的三维、非等温的CFD 模型的可靠性，建立了与文献［11］中几何尺寸、电化学和运行参数等一致的PEMFC 进行验证，图2显示两种不同工况（空气流速为0.6 m/s、阴极化学计量数为2.4 和空气流速为0.9 m/s、阴极化学计量数为3.6）的极化曲线，从图2可以看出本文模型与文献［11］中的极化曲线在不同工况下吻合良好，两组极化曲线的对比最大误差分别为1.72%和2.43%，在合理范围内。因此，可以验证本文所建模型的可靠性。

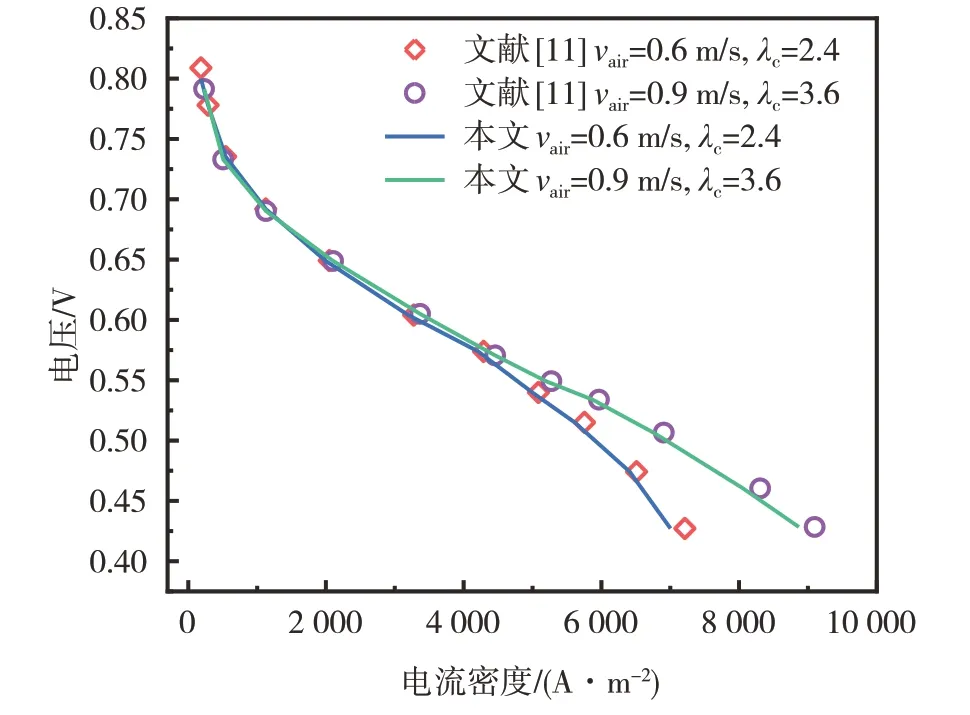
图2 不同工况下的模型验证

3 结果分析

3.1 温度分析

图3 为Case1 的垂直方向不同电压的温度分布图。可以看出随着电压的逐渐减低和电堆电化学反应的进行，电堆的温度逐渐升高，并且电堆内部的高温主要集中在膜电极上，尤其是催化层和膜温度最高。同时，也可以发现电堆温度从上到下以Unit3为轴呈对称式分布，电堆中间层和边缘层的温度存在着明显的不均匀性现象，其他参数包括氧气浓度、水浓度、电流密度等呈现同样的对称分布，而且由于Case2 和Case3 孔隙率也是对称式分布，其温度和其他参数等与Case1 分布规律一致，都是以Unit 3为轴对称分布。因此，本文后续主要分析Unit1、Unit2、Unit3 3层的性能差异和均匀性。

图3 不同运行电压下垂直方向的温度分布

减小电堆内部边缘层和中间层的温度差值，提升电堆内部温度的均匀性对电堆的使用寿命至关重要，因此本文分析了3 种Case 下电堆内部的温度分布情况，如图4（a）所示，可见从电堆进气口到出口温度逐渐上升。同时，由于气体扩散层不同孔隙率的设置Case2和Case3的温度要高于Case1，为了衡量不同电池单元之间的温度均匀性，本文计算了Unit1和Unit2、Unit1 和Unit3 的平均温度差值，如图4（b）所示，其中Case2的Unit1和Unit2、Unit1和Unit3温度差值最小，因此Case2可以有效减小中间层和边缘层中间的温度差值，提高电堆内部温度的均匀性。

图4 分层设计对电堆温度分布影响

3.2 反应物与产物分析

氧气和水的摩尔分数的大小也会影响电堆性能，电堆内不同层之间氧气和水的摩尔分数的一致性对电堆性能、温度也有严重的影响。本节分析了电堆内部的氧气和水的摩尔分数，以及不同层的浓度差值大小，图5（a）是3 种Case 的电堆氧气摩尔分数，可以看出Case2 和Case3 的摩尔分数都高于Case1，由于Case3边缘层的孔隙率较大，所以氧气摩尔分数最高。然而从图5（b）可以看出，不同Case 的不同层之间的氧气摩尔分数差值和大小并不完全一致，Case1 不同单元之间的氧气摩尔分数差值最大，Case3 次之，Case2 的氧气摩尔分数差值最小，因此Case2 的不同单元的氧气摩尔分数的均匀性与温度均匀性保持相同的趋势。

电堆内部水的主要来源是阴阳极进气加湿和电化学反应生成的水，水的含量对于反应气体在膜电极传输和膜性能至关重要，水浓度的均匀性也影响着电堆的整体性能。图6（a）为3种Case下电堆内水摩尔分数的分布，其分布规律和含量与氧气分布规律和含量接近，因为氧气浓度高的地方电化学反应程度高，生成的水更多。可以看出Case3 的水摩尔分数最高，但从图6（b）可以看出，中间单元和边缘单元的水摩尔分数差值仍然是Case2 和Case3 较小，且Case2最小。

图6 分层设计对电堆水分布影响

3.3 电流密度分析

图7（a）为3 种Case 的电堆5 层单元的膜电流密度分布图，可以看出电流密度沿着反应物流动方向逐渐降低，这与氧气摩尔分数的分布趋势一致。图7（b）展示了3 种Case 的极化曲线，可以看出3 条曲线在大于0.6 V 时基本上没有差别，在电压为0.4 V时，Case2 比Case1 电流密度提升了1.58%，Case3 比Case1 电流密度提升了2.38%。膜电流密度是电堆输出性能的关键指标。不同单元的电流密度的均匀性对于电堆的稳定输出和耐久性都有重要影响。而且电流密度增大不一定会提升不同单元之间的电流密度均匀性。图7（c）显示了3种Case不同单元之间的电流密度差值，以评价中间单元和边缘单元电流密度的均匀性，可以看出不同单元之间的电流密度均匀性仍是Case2 最佳，这与上文分析的温度、氧气摩尔分数、水摩尔分数等现象一致。

图7 分层设计对电堆电流密度分布影响

3.4 缺气工况分析

车用电堆在实际运行中可能会遇到各种不同的工况，工况对于电堆的稳定运行、输出性能、使用寿命都有着严重的影响。因此本节将阴极进气流速设置为原来的60%以模拟缺气工况，分析了不同Case的电堆温度和氧气摩尔分数的均匀性。图8（a）为缺气工况下的电堆温度分布，可以看出缺气工况下的温度明显低于图4（a）的正常运行工况，这是因为缺气导致催化层内部氧气浓度降低，电化学反应程度降低，热量产生减少。图8（b）是缺气工况不同Case不同单元的平均温度差值，图中表明Case2 仍然有着最低的温度差值。

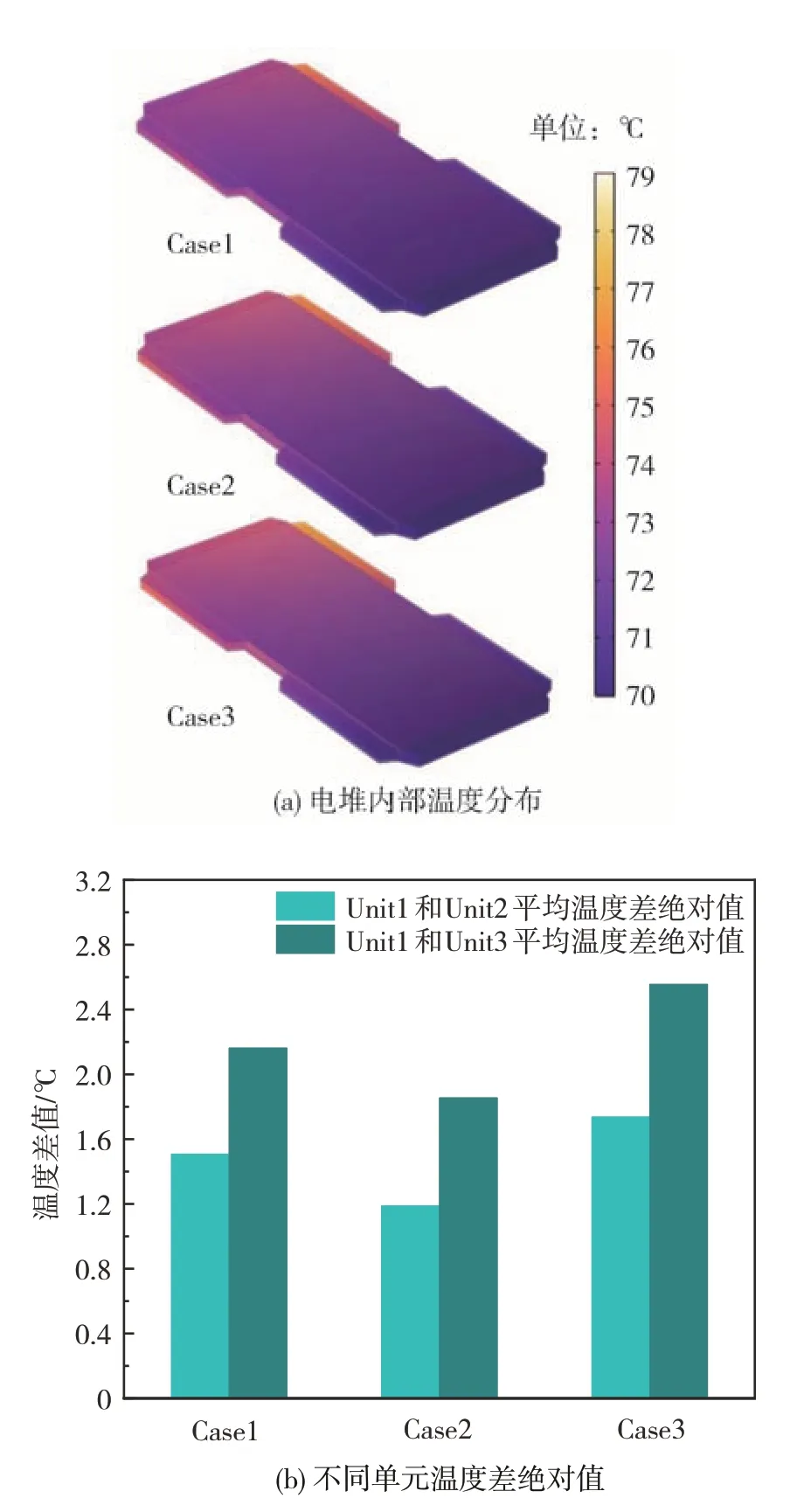
图8 缺气工况下对电堆温度分布影响

图9（a）显示了缺气工况下的电堆氧气摩尔分数分布，可以看出缺气工况下的氧气摩尔分数明显低于图5（a）的常规运行工况，尤其是在出口附近，这一现象更为明显，Case3 相比其他Case 仍然是氧气浓度最高的。另外从图9（b）可以看出，Case2 氧气浓度差值与图8（b）的温度差值趋势一致，都是最小的，因此也说明了在缺气工况下，Case2 可以改善中间层和边缘层温度、氧气摩尔分数之间的均匀性，这有利于电堆在缺气工况下的稳定运行和使用寿命的延长。

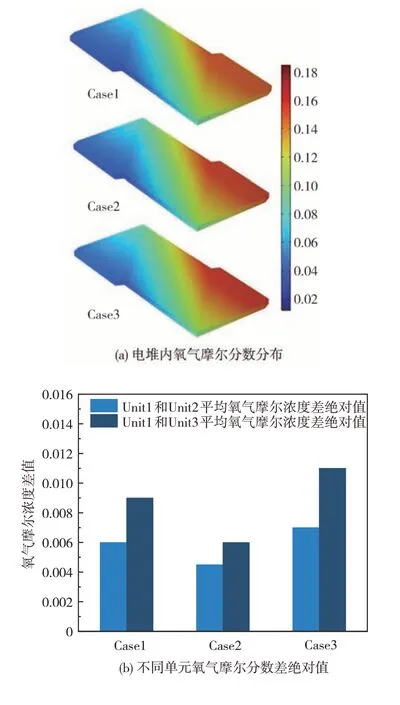
图9 缺气工况下氧气浓度分析

4 结论

本文建立了包含5 层单元的PEMFC 短电堆模型，分别在阴极和阳极气体扩散层设置了不同的梯度孔隙来改善短电堆中间单元与边缘单元的温度、反应物等不均匀性问题，通过数值模拟得到了以下结论。

（1） Case2和Case3由于较大的孔隙率电堆内部温度都略高于Case1，但是Case2 可以有效减小中间层和边缘层之间的温差，提升电堆内部温度的均匀性。

（2） 不同Case 的不同单元之间的反应物和产物浓度差值和浓度大小并不完全一致，Case2 的氧气、水摩尔分数差值最小，均匀性最好，而Case3 的氧气、水摩尔分数最高。

（3） 电堆5层膜电流密度的分布趋势与温度、氧气浓度等保持一致，且Case2 的不同单元的膜电流密度仍然有着最小的差值和最好的均匀性。

（4） 在缺气工况下，Case2 由于其梯度孔隙率从内层到外层逐渐增大的设置，仍然有着最佳的温度和氧气摩尔分数差值，从而改善不同层之间的均匀性。