特征稀疏场景下基于标签的车辆视觉SLAM *
秦洪懋,沈国利,周云水,黄圣杰,秦晓辉,谢国涛,丁荣军
(1. 湖南大学机械与运载工程学院,长沙 410082;2. 湖南大学无锡智能控制研究院,无锡 214072)
前言
智能驾驶相关技术中,同时定位与建图(simultaneous localization and mapping, SLAM)指车辆在未知环境中运动时,借助特定传感器获取环境信息、建立地图模型并估计自身运动的过程。在现有的SLAM 技术中,视觉特征点法通过提取图像特征点、计算描述子与特征匹配等过程估计相机的位姿,典 型 的 特 征 点 法SLAM 如PTAM[1]、ORBSLAM[2-4]等。
自然特征稳定性差,易受外界因素干扰,在定位过程中,若场景的纹理特征稀疏,定位系统难以提取足够特征点,使得帧间数据不能有效关联,导致系统因约束不足而无法精确估计位姿,严重限制了算法在实际场景的应用。针对场景特征稀疏问题,已有诸多学者进行研究,其解决方法根据原理可分为:基于图像增强的方法、挖掘图像额外特征的方法与引入人工标签的方法。
在基于图像增强的方法中,Banik 等[5]使用直方图均衡法调整图像灰度值,增强特征稀疏图像的对比度,提高昏暗环境下纹理的清晰度,改善图像质量以保证特征的稳定识别;Wang 等[6]提出一种多层图像表示法来解决环境特征稀疏问题,基于信息论计算对比度增强的最佳参数,通过不同程度的对比度增强进行图像优化,改进特征点的检测与匹配。但是基于图像增强的方法自适应性差,依赖人工调整参数,图像增强也会导致噪点增加,反而影响特征的匹配,无法完美地解决场景特征稀疏问题。
在挖掘图像额外特征的方法中,Pumarola 等[7]提出了一种基于点线特征的PL-SLAM,针对低纹理的特征稀疏环境,将场景结构化边缘作为线特征并借助端点参数化,用于帧间的特征匹配与位姿估计;He 等[8]提出基于点和线特征的视觉惯性里程计PLVIO,借助图像点线特征的提取和匹配进行位姿计算,充分利用环境的几何结构信息,并通过与惯性测量结果的紧耦合获得最优的位姿估计;Sun等[9]通过融合线面特征估计相机位姿,在特征稀疏场景,利用边缘和平面提取线面特征,构建运动估计约束,并根据面特征的置信度调整相关线特征的权重。通过挖掘图像纹理外的线面特征,可解决场景特征稀疏时的位姿估计问题,但是线面特征易被遮挡,优化效果不够稳定,且处理特征时的计算量巨大,严重增加系统的资源占用。
在引入人工标签的方法中,Chen 等[10]在室内场景布置标签,通过标定获得标签的全局位姿,并建立标签地图,在定位时使用惯性测量数据初步估计车辆位姿,同时进行标签检测,基于标签位姿优化定位结果;Chakraborty 等[11]在走廊、隧道等具有相似特征的场景中,部署视觉标签并预先标定,借助标签区分相似环境,在检测到重复标签时进行回环检测,并借助标签绝对位姿优化定位结果;Pfrommer 等[12]提出了一个用于构建标签地图的TagSLAM 系统,在场景中部署标签,使用相机同时观测多个标签,计算同一帧图像中各标签的相对位姿,并在运动过程中持续更新优化各标签的位置关系,最终构建出所有标签的相对位姿地图;Roos-Hoefgeest等[13]通过在车辆上布置8 个相机构建相机位姿约束,检测在同一时刻车辆周围的所有标签,并获取相对位姿估计,在车辆运动时通过相对位姿变换更新标签地图,然后基于该地图对车辆进行定位。
相比于图像增强和挖掘额外特征,引入人工标签受到环境的限制少,稳定性更高,更适用于解决特征稀疏问题。但当前基于人工标签的方法仍存在以下不足。(1)标签标定成本过高:标签常常以较短间距无规律地分布在场景中,初次布置与后续维护都须对标签位姿进行人工标定,工作量巨大。(2)对标签形状变化敏感:在运动中相机难以时刻观测到清晰的标签,相机的偏转常常导致标签发生变形,当前通过顶点像素坐标获取标签位姿估计的方法不够稳定,易出现位姿抖动。(3)标签信息利用率低:当前基于标签的定位方法对标签内部角点的利用率不足,位姿估计时引入的约束条件较少,难以获得稳定的标签位姿,无法保证地图的一致性,影响系统的精度和稳定性。
为解决上述问题,本文提出一种融合标签的视觉SLAM 系统,其主要创新点包括:(1)充分利用标签信息,通过提取标签内部角点引入额外约束获得更稳定、更精准的标签位姿估计,降低当标签存在变形时的位姿抖动;(2)基于内外角点约束、标签位姿优化模型和视觉里程计构建低漂移、全局一致的地图,提高标签地图的精度并保证建图过程的稳定性;(3)设计融合标签检测的视觉SLAM 算法框架,基于标签地图估计车辆位姿,并对标签地图和车辆位姿进行联合优化,显著提升建图精度与系统鲁棒性。
1 系统概述
本文提出的基于标签的视觉SLAM 方法,以AprilTag[15]作为视觉标签,借鉴ORB-SLAM3 设计基于标签定位的系统框架,如图1 所示。本方法集成为系统的标签定位线程,主要包括检测标签、内外角点提取、估计标签位姿、构建标签位姿地图和恢复相机位姿5 个模块,并在后续线程中优化标签与相机的位姿。

图1 系统架构
系统获取图像并完成特征提取与匹配后,进入标签处理线程,检测图像中是否存在标签。若存在,则基于内外角点约束,筛选出最优的标签并进行内外角点提取,估计标签相对于相机的位姿。若系统中未发现标签地图文件,则基于特征点对相机位姿进行初步估计,计算标签的全局位姿,进而建立标签位姿地图,然后返回ORB 跟踪线程,对相机位姿和标签地图进行优化;若系统中存在标签地图文件,则使用标签位姿地图获取相机位姿的初步估计,结合ORB中的地图点进行优化获得精确的定位结果。
2 内外角点约束
AprilTag 的开发者提供了检测标签和估计位姿的算法[16],流程如图2 所示。将输入的标签图像二值化后,通过边缘检测获得图像中所有线段;然后搜索闭合的凸多边形,并筛选出四边形;获取各四边形内的像素排列,解码得到标签的编号;最后计算4 个顶点的像素坐标,并通过直接线性变换估计标签位姿。
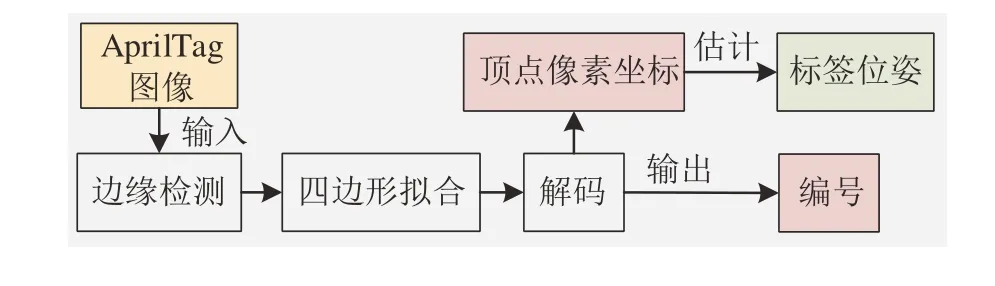
图2 AprilTag检测与位姿估计流程
但是该方法对标签的利用率有限,仅依赖4 个顶点计算位姿,稳定性不足,常出现位姿跳动。因此,本文设计了标签内外角点约束策略,使用标签外边缘顶点和内部角点共同进行位姿估计,提高标签信息的利用率,通过增加约束降低位姿抖动,保证地图的全局一致性。
在进行标签检测时,若图像中存在多个标签,需要根据标签的大小、变形程度等标准选择距离最近、变形最小的标签用于位姿估计。本文方法制定的标签评价策略为
式中:Simg为图像像素面积;Stag为标签的像素面积,由对角线乘积近似;k1~k4为标签4 条边的斜率。选择W最小的标签,用于后续的位姿估计。
在标签内部提取的若干角点中,通过迭代匹配筛选出最优的4 个角点用于位姿估计,详细步骤如图3所示。筛选获得最优标签后,如图3 (a)所示,使用顶点坐标划分角点提取范围,以减少外部噪点的影响。通过Shi-Tomasi 算法[18]提取标签的内部角点,并借助亚像素细化算法提高角点坐标的精度。

图3 内部角点的提取与匹配
计算角点对应的三维空间点时,通过射影变换获得规则化标签,如图3 (b)所示。若标签某一顶点像素坐标为[x1,x2]T,射影变换后的像素坐标为[x′1,x′2]T,则该过程可表示为
式中Hp为3×3 的射影变换矩阵。通过4 个顶点求解出Hp后,对内部角点进行射影变换,然后进行二位像素点到三维空间点的匹配。
AprilTag 由8×8 的方格组成,如图3 (e)所示,建立与像素坐标系对应的方格坐标系,角点的像素坐标、方格坐标与图3 (f) 中的标签平面坐标存在对应关系。但标签边缘一般与像素坐标轴不平行,如图4 所示,沿标签的边缘和边缘法线构建新的坐标系,用于方格坐标计算。
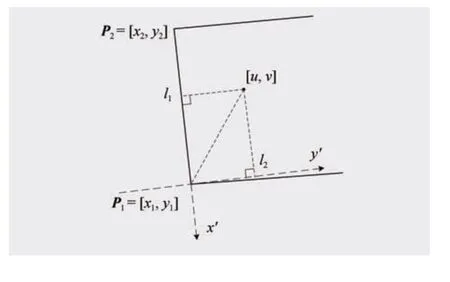
图4 标签边缘坐标系
图4 中角点的像素坐标为 [u,v],P1、P2为标签的2个顶点,沿P1P2及其法线方向建立坐标系,角点在该坐标系下的坐标[l1,l2]和单位方格边长Δl为
将坐标[l1,l2]除以单位方格边长Δl取整得到该点的方格坐标,其对应的三维空间点坐标为方格坐标乘以实际方格边长。
由于噪声点和射影变换的影响,可能存在角点不是方格顶点或方格坐标错误的情况,影响标签的位姿估计。因此借鉴RANSAC 算法,以4 个角点一组,通过选取不同的角点进行迭代,求解最优的单应矩阵。已知标签所在二维平面内一点的坐标P=[x,y]T,和对应的相机投影平面的投影点的坐标p=[u,v]T,由投影关系得:
式中:s为尺度;H矩阵为8个自由度的3×3矩阵。使用4对点构建8个方程对H矩阵进行求解,计算角点Pi的投影误差:
若误差小于1 像素则将该点标记为内点,然后对所有内点重复此过程,并更新迭代次数k:
式中:p为置信度,取0.995;w为内点所占的比例;m为最少所需点对,取4。
迭代完成后,得到最优的H矩阵,在最终的内点集合中选择投影误差最小的4 个内部角点作为新约束,与外部4个顶点共同用于标签位姿的估计。
3 标签位姿地图
3.1 标签位姿优化模型
基于内外角点约束策略获得当前场景中最优标签的4个顶点与4个内点,进而构建标签位姿优化模型,通过最小化重投影误差迭代求解。若已知某三维空间点坐标P=[X,Y,Z]T及其投影的像素坐标p=[u,v]T,重投影误差为e为
式中:K为相机内参矩阵;ξ为位姿变换矩阵T对应的李代数;ξ∧为ξ的反对称矩阵。假设误差函数为f(x),进行1阶泰勒展开得到增量方程:
式中JT为雅可比矩阵,位姿增量为Δξ,不断迭代并更新T= exp(Δξ∧)T,直到Δξ足够小,此时便得到最优的T,即标签相对于相机的位姿。
如图5所示,在相机和标签外的一点P,与相机、标签位于同一空间坐标系内,定义该点在世界坐标系下的坐标为Pw,在相机坐标系内的坐标为Pc,在标签坐标系下的坐标为Pt。则Pw与Pc、Pc与Pt之间的位姿变换关系为

图5 坐标转换关系
式中:Tcw为相机坐标系到世界坐标系的位姿转换矩阵;Ttc为标签坐标系到相机坐标系的位姿转换矩阵。所以Pw与Pt之间的关系为
因此标签坐标系到世界坐标系的位姿转换矩阵Ttw表示为
其中,相机的全局位姿Tcw由ORB 提供初步估计,标签相对于相机的位姿Ttc通过内外角点估计,最终由式 (14) 计算得到当前标签的全局位姿Ttw,作为标签地图的初值。
3.2 地图构建与优化策略
在估计标签位姿时,相机会多次观测到同一个标签,所以通过n次观测可估计出n个位姿,由于存在误差,这些位姿在真实值附近浮动。为提高标签位姿地图的精度,当n足够大时,标签位姿估计数据满足正态分布,通过3σ原则剔除误差过大的数据,然后计算剩余位姿的均值作为标签的全局位姿。
标签的位姿包括旋转与平移:
式中:R为3 × 3 的旋转矩阵;t为三维平移向量。平移的均值μt和方差σ2t可直接计算,旋转则将矩阵转换为欧拉角,计算欧拉角的均值μθ和方差σ2θ。剔除[μ- 3σ,μ+ 3σ]外的数据,计算剩余位姿矩阵的平移向量均值tˉ和旋转矩阵的四元数中间插值,若剩余m个位姿,平移向量均值为,旋转矩阵R对应的四元数为Q=[q0,q1,q2,q3]T,进行插值:
将该中间插值转换为旋转矩阵,则该标签最终的位姿矩阵为
若n不够大,例如n<10,则3σ原则失效,直接对位姿排序,选择中间值作为标签最终位姿。最后,以标签的编号为索引,存储所有标签优化后的全局位姿,得到标签位姿地图。
4 基于标签的定位方法
4.1 相机位姿的初步估计
完成标签地图构建后,借助该地图对相机进行定位。当图像中检测到标签后,系统加载地图文件获取标签位姿,并由该位姿获取相机位姿的初步估计。
基于内外角点约束策略和标签位姿优化模型估计标签相对于相机的位姿Ttc;通过读取标签地图文件,以编号为索引查找得到标签在世界坐标系下的全局位姿Ttw,则相机的全局位姿表示为
获取相机位姿的初步估计后,为了提高定位结果的精度和稳定性,借助地图点进行优化。
4.2 相机位姿的精确估计与优化
4.2.1 位姿优化方案
完成对相机全局位姿的初步估计后,加入ORB-SLAM3 中的地图点构建g2o 问题来优化相机的位姿,以获得精确的定位结果。如图6 所示,以地图点位姿Pm、相机位姿Twc、标签位姿Ttw作为图的顶点,优化相机位姿与标签地图。
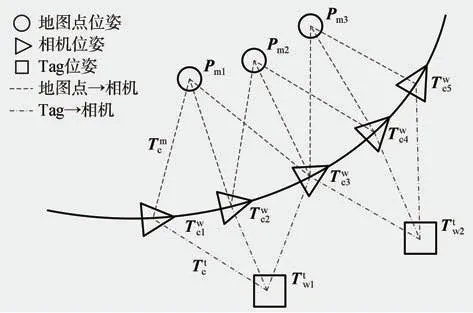
图6 位姿图优化
设u为地图点观测的二维坐标,uˉ为地图点的重投影位置的二维坐标,则重投影误差为
构建误差函数:
对相机的位姿Twc和标签位姿Ttw进行优化,并通过卡方检验剔除地图外点。
4.2.2 卡方检验
每次优化完成后,均通过卡方检验筛选出地图点中的外点并剔除。计算各个地图点的重投影误差e,该误差服从高斯分布e~N(0,Σ),在ORB-SLAM3中图像金字塔的缩放比为1.2,协方差Σ由图像金字塔的层级n决定:
使用协方差对重投影误差进行加权,计算向量的内积作为阈值:
r服从自由度为2的卡方分布,在0.05的显著性水平(95%的准确率)下,卡方检验的拒绝域为
位于拒绝域内的点被判定为外点,不再参与后续对相机位姿的优化,经过四次优化后最终获得精确的相机位姿。
5 试验测试
本文通过实车试验对系统的综合性能进行测试,为验证不同场景中算法的通用性,分别在室内回型走廊与地下停车场进行试验。视觉标签选用AprilTag 的tag36h11 序列,标签的尺寸为0.16 m×0.16 m,使用realsense-D455 相机,系统在配备intel i7-12700H CPU、2.3Hz8 核、16GB RAM、Linux 系统的计算机上运行。
5.1 内外角点约束效果与视角鲁棒性测试
在室内回型走廊环境进行试验,走廊墙壁和地板的表面缺乏纹理,如图7 (a)所示,属于特征稀疏场景;使用的试验小车如图7 (b)所示,通过手动控制。在该场景中,通过比较有无内外角点约束时的运行轨迹和建图精度,验证该策略的有效性;改变相机观测标签的视角,测试当标签发生变形时系统的定位效果。

图7 试验小车与测试环境
5.1.1 基于内外角点约束策略的定位效果测试
如图8 (a),相机安装在小车侧面,走廊内标签的布置如图8 (b)所示,分别在有无内外角点约束时进行建图与定位。运动轨迹如图9 所示,未加入内外角点约束的方法存在位姿抖动;图10 为二者在x、y、z3 轴的位移和横滚角(roll)、俯仰角(pitch)、偏航角(yaw)上的对比,位移最大跳动约0.2 m,角度最大跳动约10°;本文方法得到的结果在位移与角度上均过渡平滑,通过引入内外角点约束,显著提高了特征稀疏时系统的鲁棒性。

图8 相机位置与标签场景
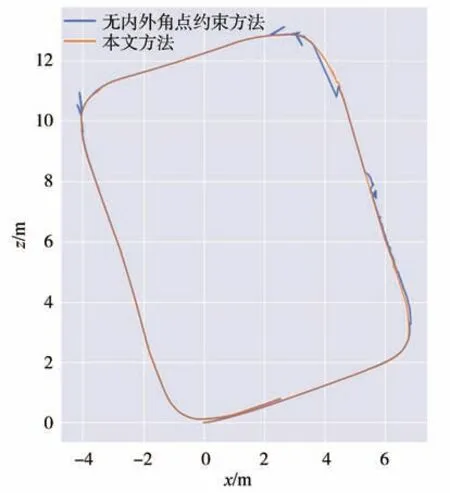
图9 无内外角点约束方法与本文方法的轨迹对比

图10 无内外角点约束方法与本文方法的轨迹在位移与角度上的对比
标签的位置示意图如图11 所示,完成标签位姿地图的构建后,计算编号0~5、6~15、16~21、22~31标签的相对距离,记录5 次试验结果,并计算最大相对误差。结果如表1 所示,使用本文方法得到的相对误差范围保持在0.05 m 以内,相比于无内外角点约束策略的方法误差缩小了60%以上,显著提高了系统对特征稀疏场景适应性,有效地保证了地图的一致性。

表1 标签间距相对误差
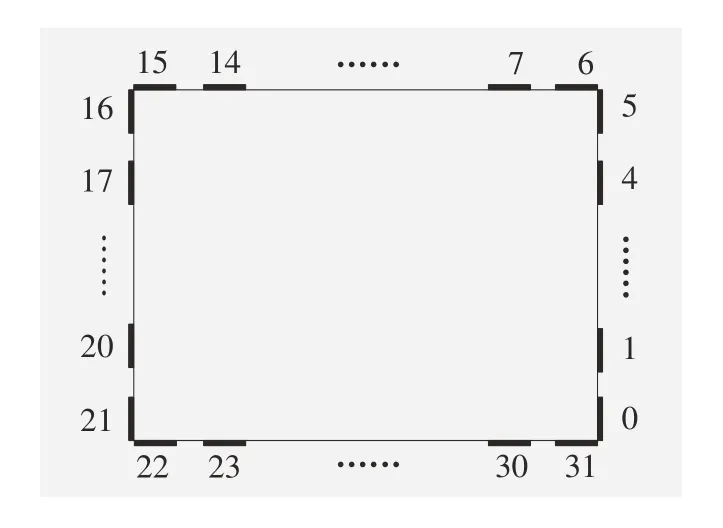
图11 标签位置示意图
5.1.2 视角鲁棒性测试
相机安装位置如图12 (a)所示,位于小车前端,走廊地面的标签布置如图12 (b)所示,从相机视角观察标签时,标签存在变形,测试当前场景下系统建图与定位的效果,验证本文所提方法对标签存在变形时的鲁棒性。系统的运行效果如图13 所示,相机视角偏转导致标签变形时,本文方法依旧能正常进行标签检测。

图12 相机位置与标签场景

图13 系统运行效果
改变相机视角后,未加入内外角点约束的方法与本文方法的相机运动轨迹对比结果如图14 所示,二者均得到了平滑的轨迹,本文方法轨迹的偏移量更小。试验结果说明,本文提出的方案有效降低了标签存在变形时的位姿抖动,对相机视角和标签位置的要求更加宽松,提高了定位系统的鲁棒性。
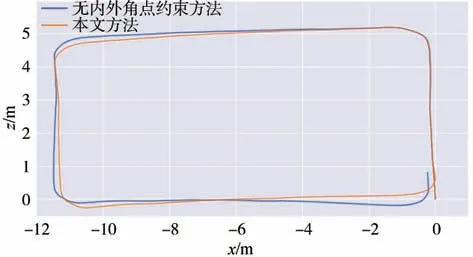
图14 相机视角改变后轨迹对比
5.2 基于标签的视觉SLAM 算法性能测试
如图15 (a)所示,将本文算法部署至智能车辆平台,在室内停车场中,通过人工驾驶车辆验证算法在实际特征稀疏场景下的应用效果。相机安装于车辆右侧靠前位置,标签布置如图15 (b)所示,在该场景下进行建图与定位,通过对比帧间特征关联成功率、重复定位误差、各模块耗时与内存占用程度,综合评估ORB-SLAM3与本文算法在各维度上的优劣。

图15 试验车辆与室内停车场
5.2.1 帧间特征关联成功率对比
成功关联帧间特征是构建优化函数、解算车辆位姿的前提条件,其成功率能从侧面反映算法提取场景特征、构建有效约束的能力。在室内停车场进行5 次试验,并计算成功关联的特征点比例,如表2所示,相比于ORB-SLAM3,本文所提方法的特征关联成功率提高了10%以上,在特征稀疏场景下依旧能够建立有效约束。
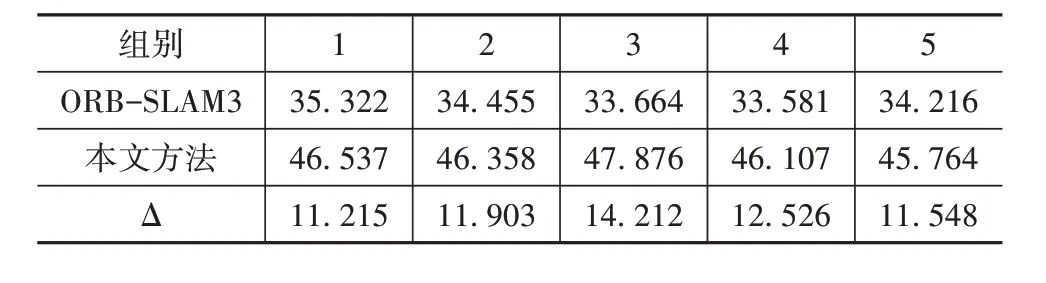
表2 特征点关联成功率 %
5.2.2 定位精度测试
室内停车场环境中,驾驶车辆绕行一周,运动路线总长约60 m,图16 为ORB-SLAM3 与本文方法生成的相机运动轨迹对比,二者均获得了平滑的轨迹,位移与角度对比结果如图17 所示,由本文所提方法生成的轨迹在平移与角度上的漂移略小。

图16 室内停车场运行轨迹对比
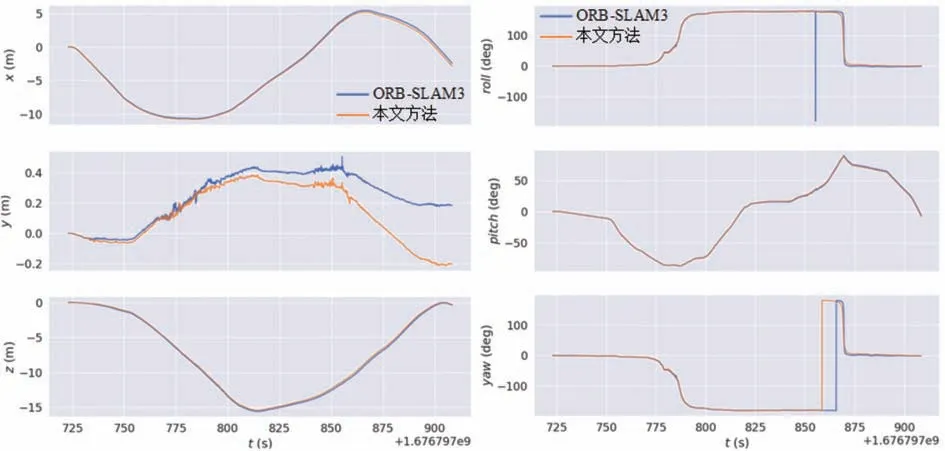
图17 ORB-SLAM3与本文方法的轨迹在位移与角度上的对比
记录车辆在室内停车场中运动的起点位置和终点位置,在ORB-SLAM3 与本文所提方法完成定位后,计算基于视觉里程计和基于地图两种方式的重复定位误差,共进行5 组试验,结果如表3 所示。本文所提方法的定位精度与ORB-SLAM3 相比平均提升了30%以上。本文提出的融合标签的视觉SLAM算法显著提高了车辆在稀疏场景下的定位精度,同时保证了地图的一致性。
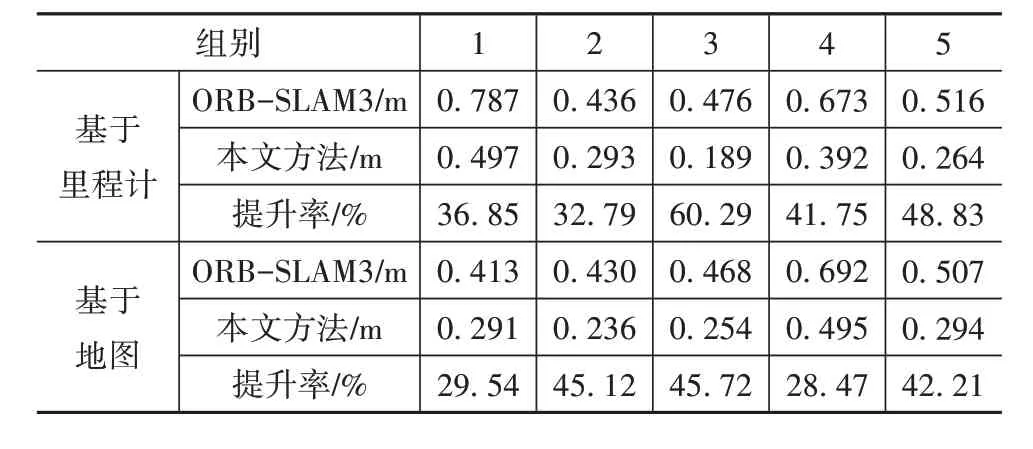
表3 重复定位误差对比
5.2.3 效率与实时性测试
系统运行时,ORB-SLAM3 占用内存0.9 GB,约6.2%,本文所提方法占用内存1.0 GB,约6.6%,二者的效率相差不大。记录10 次试验中定位算法运行的时间,由于本文所提方法的特征提取模块加入了标签检测,使耗时略微增加,计算平均耗时如表4所示,ORB-SLAM3 与本文所提方法的平均总耗时分别为37.969 和63.057 ms,本文所提出的算法可达到15 帧/s 的处理速度,满足车辆在特征稀疏场景中的定位要求,后续将针对标签检测的效率进行优化。
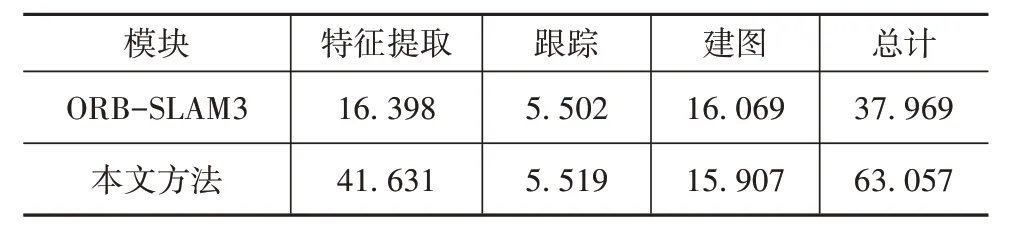
表4 算法各模块平均耗时 ms
6 结论
针对车辆在特征稀疏场景下定位时,特征数量不足和稳定性差等问题,本文提出了一种基于标签的视觉SLAM 方法,借助内外角点约束策略和标签位姿优化模型,融合标签与视觉里程计构建全局一致的地图,从而基于该地图与视觉特征点进行定位,并联合优化标签地图与车辆位姿。本文提出的构建标签位姿地图的方法兼顾一致性与稳定性,通过与ORB-SLAM3 的算法融合,并搭建试验平台测试系统的定位性能,结果表明,相比于ORB-SLAM3 和传统标签定位方案,本文提出的方法显著降低了相机的位姿漂移,提高了基于标签定位方法的精度与鲁棒性,有利于保障智能车辆的行驶安全。
后续工作将优化标签检测的效率,进一步提高算法的实时性。

